розробка уроку на тему "Теорема косинусів."

УРОК № 4

Тема уроку. Теорема косинусів.

Мета уроку: вивчення теореми косинусів. Формування вмінь учнів застосовувати теорему косинусів до розв'язування задач.

Тип уроку:  комбінований.

Наочність і обладнання: таблиця «Співвідношення між сторонами і кутами трикутника»[13].

Вимоги до рівня підготовки учнів: формулюють теорему косинусів та доводять її.

Хід уроку

I. Перевірка домашнього завдання

Перевірити наявність виконаних домашніх завдань та відпо­вісти на запитання, які виникли в учнів у ході їх розв'язування.

ІІ. Аналіз результатів самостійної роботи

ІІІ. Мотивація навчальної діяльності

Ми приступаємо до вивчення теми «Розв'язування трикутників».

Розв'язати трикутник означає знайти відомі елементи трикут­ника (сторони, кути) за даними відомими елементами. У 8-му кла­сі ви вже навчилися розв'язувати прямокутні трикутники. Прямо­кутний трикутник визначається за двома елементами, серед яких є хоча б один лінійний елемент (сторона). Ви вмієте знаходити невідомі елементи прямокутного трикутника, якщо дано: катет і гіпотенузу; гіпотенузу і гострий кут; катет і прилеглий гострий кут; катет і протилежний гострий кут.

Щоб розв'язати довільний (не прямокутний) трикутник, треба знати три елементи, серед яких має бути хоча б один лі­нійний.

Зараз ви ознайомитеся з теоремою, яка дозволяє за двома сторонами і кутом між ними знаходити третю сторону, невідомі кути трикутника. Ця теорема називається теоремою коси­нусів.

IV. Сприймання й усвідомлення нового матеріалу

Вивчення теореми косинусів

Сформулюємо теорему та ознайомимо з її доведенням учнів.

Теорема. Квадрат будь-якої сторони трикутника дорівнює сумі квадратів двох інших сторін без подвоєного добутку цих сторін на косинус кута між ними.

Доведення

Нехай задано трикутник ABC, доведемо, що

а² = b² + с² – 2bc cosα, де а = ВС, b = AC, с = АВ, A = α.

Розглянемо три випадки: якщо кут А є гострим, тупим і пря­мим.

1-й випадок

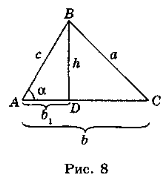
Якщо кут А гострий (рис. 8), то проведемо висоту BD і розглянемо пря­мокутний трикутник BDC. У ньому ВС² = DC² + BD² або a² = (b – b₁)² + h².              (1)

Виразимо b₁ і h через основні елементи трикутника ABC. Із трикутника ABD миємо: h = csinα, b₁ = ccosα. Замінивши h і b₁ у виразі (1) їх значеннями, знай­демо:

a² = (b – ccosα)² + с²sin²α = b² – 2bccosα + с²cos²α + c²sin²α =

= b² – 2bccosα + c²(sin²α + cos²α) = b² – 2bccosα + c² · 1 = b² + c² – 2bccosα.

Отже, a² = b² + c² – 2bccosα, що і треба було довести.

2-й випадок

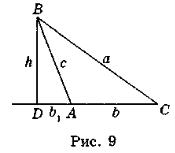
Нехай кут А тупий (рис. 9). Із вершини В проведемо висоту BD на продовження сторони АС. Із прямокутного трикутника BDC маємо:

BC² = BD² + DC² або a² = h² + (b + b₁)². (2)

Значення h і b₁ виразимо через основні елементи трикутни­ка ABC. Із трикутника ABD маємо: h = csin(180°- α) = csinα, b₁ = ccos(180° - α) = -ccosα. Замінивши h і b₁ у виразі (2) їх значен­нями, після деяких перетворень маємо:

a² = c²sin²α + (b – ccosα) = с²sin²α + b² – 2bccosα + c²cos²α = (c²sin²α +           + c²cos²α) + b² – 2bccosα = c²(sin²α + cos²α) + b² – 2bccosα = b² + c² – 2bccosα.

Отже, a² = b² + c² – 2bccosα, що і треба було довести.

3-й випадок

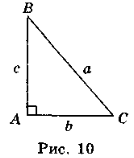
Нехай кут А прямий, α = 90° (рис. 10). У цьому випадку cosα = cos 90° = 0, отже, маємо:

b² + c² – 2bccosα = b² + c² – 2bc · 0 = b² + с². (3)

Але за теоремою Піфагора маємо: b² + с² = а². (4)

Порівнявши вирази (3) і (4), отримаємо: a² = b² + c² – 2bccosα. Теорему, доведено.

Теорему косинусів іноді називають узагальненою теоремою Піфагора. Така назва пояснюється тим, що в теоремі косинусів міститься як частковий випадок теорема Піфагора. Справді, якщо в трикутнику ABC кут А прямий, то cos A =   = cos 90° = 0, і за теоремою косинусів одержуємо а² = b² + с², тобто квадрат гіпотенузи дорівнює сумі квадратів катетів.

Розв'язування задач

При розв'язуванні цих задач слід домовитися, що сторони трикутника позначатимемо буквами a, b, с, а протилежні їм кути (при вершинах А, В, С) — грецькими літерами α, β, γ. Слід також згадати значення тригонометричних функцій деяких кутів (табл. 1), зазначивши, що синуси суміжних кутів рівні, а коси­нуси суміжних кутів — протилежні числа: sin(180°- α) = sinα, cos(180°- α) = = -cosα. Розв'яжемо такі задачі.

1. Дві сторони трикутника дорівнюють 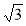см і 1 см, а кут між ними 30°. Знайдіть третю сторону трикутника. (Відповідь. 1 см.)
2. Знайдіть третю сторону трикутника, якщо дві інші сторони до­рівнюють 1 см і 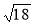см і утворюють кут 135°. (Відповідь. 5 см.)

V. Закріплення й осмислення нового матеріалу

Розв'язування задач

1. Сторони трикутника дорівнюють 1 см, 3 см і 5 см. Знай­діть кут, який лежить проти найбільшої сторони.

Розв'язання

Нехай у трикутнику ABC а = 1 см, b = 3 см, с = 5 см. За теоремою косинусів маємо: с² = b²+ a² – 2bacosγ, тоді 5² = 1² + – 2 · 1 · 3cosγ;   25 = 19 – 6cosγ; 6cosγ = - 6; cosγ = = = ;

тоді γ = 180° - 45° = 135°.

Відповідь. 135°.

2. Дві сторони трикутника а і с дорівнюють 5 см і 7 см, а кут γ дорівнює 60°. Знайдіть сторону b.

Розв'язання

За теорему косинусів маємо:

с² = а² + b² – 2abcosγ, або 7² = 5² + b² – 2 · 5 ·  bcos60°,

звідси 49 = 25 + b² – 5b, або b² – 5b – 24 = 0. Роз­в'язавши рівняння, одержимо b₁ = 8; b₂ = -3. Оскільки b > 0, то значення b₂ не задовольняє умову задачі.

Відповідь. 8 см.

3. У трикутнику дві сторони дорівнюють 5 м і 6 м, а синус кута між ними дорівнює 0,6. Знайдіть третю сторону.

Розв'язання

Нехай а = 5 м, b = 6 м, sinγ = 0,6. Оскільки sin²γ + cos²γ = 1, то 0,36 + cos²γ = = 1, cos²γ = 0,64 і cosγ = ±0,8.

1-й випадок:

cosγ = 0,8. Тоді с² = а² + b² – 2abcosγ = 25 + 36 – 2 · 5 · 6 · 0,8 = 61 – 48 = 13; с = м.

2-й випадок:

cosγ = -0,8. Тоді с² = а² + b² – 2abcosγ = 25 + 36 + 2 · 5 · 6 · 0,8 = 61 + 48 = 109; с = м.

Відповідь. м або м.

VI. Домашнє завдання

1. Вивчити теорему косинусів.
2. Розв'язати задачу.

Сторони трикутника дорівнюють 5 м, 6 м і 7 м. Знайдіть косинуси кутів трикутника.

VII. Підбиття підсумків уроку

Завдання класу

1. Сформулюйте теорему косинусів.
2. Знайдіть невідому сторону трикутника (рис. 11).