Наслідки теореми косинусів.

УРОК № 5

Тема уроку. Наслідки теореми косинусів.

Мета уроку: виведення наслідків із теореми косинусів. Формування вмінь учнів застосовувати теорему косинусів і наслідків з неї до розв'язування задач.

Тип уроку: комбінований.

Наочність і обладнання:таблиця «Співвідношення між сторонами і кутами трикутника» [13].

Вимоги до рівня підготовки учнів: застосовують теорему косинусів до розв'язування задач.

Хід уроку

І. Перевірка домашнього завдання

Перевірити правильність виконання домашнього завдання можна за записами, зробленими на дошці до початку уроку.

Розв’язання задачі

Нехай а = 5 м, b = 6 м, с = 1 м. Тоді:

1) a² = b² + c² – 2bccosα; 25 = 36 + 49 – 2 ∙ 6 ∙ 7 ∙ cosα; 84cosα = 60;

     cosα = = = .

2) b² = a² + c² – 2accosβ; 36 = 25 + 49 – 2 ∙ 5 ∙ 7 ∙ cosβ; 70cosβ = 38;

     cosβ = = .

3) c² = a² + b² – 2abcosγ; 49 = 25 + 36 – 2 ∙ 5 ∙ 6 ∙ cosγ; 60cosγ = 12;

    cosγ = = .

Відповідь. ; ; .

Самостійне виконання вправ

Двоє учнів виконують завдання за відкидними дошками, ре­шта — у зошитах. Після закінчення роботи слід виконати само­перевірку (взаємоперевірку) під керівництвом учителя за записа­ми, що зроблені на відкидних дошках.

Варіант 1

1. Дві сторони трикутника дорівнюють 3 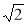см і 1 см, а кут між ними становить 135°. Знайдіть третю сторону. (Відповідь. 5 см.)
2. Сторони трикутника дорівнюють 4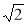см, 7 см, 5 см. Знайдіть кут, який лежить проти найменшої сторони. (Відповідь. 45°.)

Варіант 2

1. Дві сторони трикутника дорівнюють 3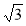см і 2 см, а кут між ними становить 60°. Знайдіть третю сторону. (Відповідь. 7 см.)
2. Сторони трикутника дорівнюють 5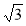см, 13 см і 7 см. Знайдіть кут, який лежить проти найменшої сторони. (Відповідь. 30°.)

II. Поетапне сприймання й усвідомлення навчального матеріалу

Застосування теореми косинусів

Формула a² = b² + c² – 2bccosα дозволяє знаходити довжину од­нієї зі сторін за відомими довжинами двох інших сторін і кутом між ними.

Теорема косинусів дозволяє також за даними сторонами три­кутника знаходити його кути.

Так, із рівності a² = b² + c² – 2bccosα одержуємо: 2bccosα = b² + с² – а², звідси cosα = .

Якщо а² < b² + с², то b² + с² – а² > 0 і, отже, cosα > 0, тобто 0° < α < 90° , кут А — гострий.

Якщо а² = b² + с², то b² + с² – а² = 0 і, отже, cosα = 0, тоб­то α = 90°, A — прямий.

Якщо а² > b² + с², то b² + с² – а² < 0 і, отже, cosα < 0, тобто 90° < α < 180°, A — тупий.

Таким чином, користуючись теоремою косинусів, можна ви­значати вид кутів (гострий, прямий, тупий) трикутника, не об­числюючи самих кутів.

Розв'язування вправ

Визначте вид кута трикутника, який лежить проти найбіль­шої сторони, якщо сторони трикутника дорівнюють:

а) 7 м, 8 м, 12 м; б) 3 см, 4 см, 5 см; в) 8, 10, 12.

Розв'язання

а) Оскільки (7² + 8²) – 12² = 49 + 64 – 144 = - 31 < 0, то кут, який лежить проти найбільшої сторони, є тупим.

б) Оскільки (3² + 4²) – 5² = 9 + 16 – 25 = 0, то кут, який лежить проти найбільшої сторони, є прямим.

в) Оскільки (8² + 10²) – 12² = 64 + 100 – 144 = 20 > 0, то кут, який лежить проти найбільшої сторони, є гострим.

Наслідки з теореми косинусів

Якщо розглянути формулу a² = b² + с² – 2bccosα, то вираз bcosα являє собою проекцію сторони b на сторону с або продовження сторони с і позначається пр_сb.

Якщо 0° < α < 90°, то із трикутника ACD (рис. 12, а) маємо

AD = bcosα = np_cb, і тоді а² = b² + с² – 2с пр_сb.

Якщо 90° < α < 180°, то із трикутника ACD (рис. 12, б) маємо

AD = b ∙ cos(l80°- α) = -bcosα = np_cb, і тоді а² = b² + c² + 2c np_cb.

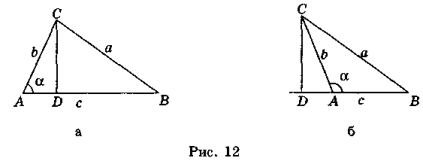
Таким чином, квадрат сторони трикутника дорівнює сумі квадратів двох інших сторін «±» подвоєний добуток однієї з них на проекцію другої на першу. Знак «+» слід брати тоді, коли протилежний кут тупий, а знак «-» — коли гострий.

Розв'язування задач

1. Сторони трикутника дорівнюють 4 м, 5 м і 6 м. Знайдіть про­екції сторін 4 м і 5 м на пряму, на якій лежить сторона 6 м.

Розв’язання

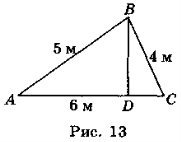
Нехай АВ = 5 м, ВС = 4 м, АС = 6 м (рис. 13).

Тоді ВС² = АВ² + АС² – 2АСпр_АСАВ; 16 = 25 + 36 – 2 ∙ 6 ∙ пр_АСАВ;

12 ∙ пр_АСАВ = 45; пр_АСАВ = = 3 (м).

Аналогічно AS² = ВС² + AC² – 2 ∙ AC ∙ np_ACВС; 25 = 16 + 36 – 2 ∙ 6 ∙ пр_АСВС; 12 ∙ пр_АсВС = 27; пр_АСВС = = 2 = 2 (м).

Відповідь. 2 м, 3м.

2. Знайдіть висоти трикутника, сторони якого дорівнюють 5 м, 6 м, 7 м.

Розв'язання

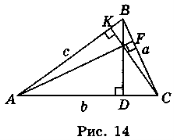
Нехай а = 5 м, b = 7 м, с = 6 м (рис. 14). Оскільки a² = b² + c² – 2b np_bc, то  25 = 49 + 36 – 14 ∙ np_bc, 14 ∙ пр_bc = 60, пр_bc = = = 4 (м), AD = 4 м.

Із трикутника ABD маємо: BD = = = 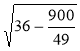= = = (м).

Оскільки b² = а² + с² – 2с пр_са, то 49 = 25 + 36 – 12 ∙ пр_са, 12 ∙ пр_са = 12, пр_са = 1, КВ = 1 м.

Із трикутника BCK маємо: СК = = = = 2 (м).

Оскільки c² = a² + b² – 2a np_ab, то 36 = 25 + 49 – 2 ∙ 5 ∙ np_ab, 10 np_ab = 38, np_ab = = = 3 (м), CF = 3м.

Із трикутника ACF маємо: AF = = =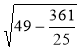= (м).

Відповідь. м, 2м, м.

ІІІ. Домашнє завдання

1. Вивчити наслідки з теореми косинусів.
2. Розв'язати задачі.

1. Дано дві сторони трикутника а і b, які дорівнюють відпо­відно 12 і 8 см та утворюють кут γ, який становить 60°. Знайдіть третю сторону трикутника і два інших кути.
2. Дано три сторони трикутника: а = 4, b = 5, с = 1. Знайдіть кути цього трикутника.
3. Дано трикутник зі сторонами а, b, с. Знайдіть висоту три­кутника, опущену на сторону с. (Цю задачу можна запропо­нувати для учнів, які цікавляться математикою.)

IV. Підбиття підсумків уроку

Завдання класу

1. Заповніть пропуски:

а) у трикутнику ABC b² = с² + ... - ...;

б) у трикутнику ABC cosβ = ;

в) якщо в трикутнику ABC a² = b² + c², то трикутник ...;

г) якщо в трикутнику ABC b² > a² + c², то B — ...;

д) якщо в трикутнику ABC b² < a² + с², то B — ....

2. Визначте вид кута трикутника, який лежить проти найбіль­шої сторони трикутника, сторони якого дорівнюють:

а) 2 см, 3 см, 4 см; б) 3 см, 4 см, 5 см; в) 4 см, 5 см, 6 см.