Календарне планування з алгебри 9 клас

УДК 373.167.1:512
М52
Рекомендовано
Міністерством освіти і науки України
(наказ МОН України від 20.03.2017 № 417)
Видано за рахунок державних коштів. Продаж заборонено
Експерти, які здійснили експертизу даного підручника під час проведення конкурсного відбору проектів підручників для 9 класу загальноосвітніх навчальних закладів
і зробили висновок про доцільність надання підручнику грифа «Рекомендовано Міністерством освіти і науки України»:
Я. П. Сисак, провідний науковий співробітник відділу алгебри
і топології Інституту математики НАН України, доктор фізико-математичних наук;
Н. В. Кравченко, методист РМЦ відділу освіти Красноградської районної державної адміністрації Харківської області, старший учитель;
Ю. О. Андрух, учитель математики
Чернівецького багатопрофільного ліцею № 4, учитель-методист
Мерзляк А. Г.
М52 Алгебра : підруч. для 9 кл. загальноосвіт. навч. закладів / А. Г. Мерзляк, В. Б. Полонський, М. С. Якір. — Х. : Гімназія, 2017. — 272 с. : іл.
ISBN 978-966-474-293-8.
УДК 373.167.1:512
© А. Г. Мерзляк, В. Б. Полонський, М. С. Якір, 2017
© ТОВ ТО «Гімназія», оригінал-макет,
ISBN 978-966-474-293-8 художнє оформлення, 2017
![]()
Любі діти!
У цьому навчальному році ви продовжите вивчати алгебру. Сподіваємося, що ви встигли полюбити цю важливу й красиву науку, а отже, з інтересом будете опановувати нові знання. Ми маємо надію, що цьому сприятиме підручник, який ви тримаєте в руках.
Ознайомтеся, будь ласка, з його структурою.
Підручник поділено на три параграфи, кожний з яких складається з пунктів. У пунктах викладено теоретичний матеріал. Найважливіші відомості виділено жирним шрифтом і курсивом. Зазвичай виклад теоретичного матеріалу завершується прикладами розв’язування задач. Ці записи можна розглядати як один із можливих зразків оформлення розв’язання.
До кожного пункту дібрано завдання для самостійного розв’язування, приступати до яких радимо лише після засвоєння теоретичного матеріалу. Серед завдань є як прості й середні за складністю вправи, так і важкі задачі, особливо ті, що позначено зірочкою (*). Свої знання можна перевірити, розв’язуючи задачі в тестовій формі з рубрики «Перевірте себе».
Десять пунктів підручника завершуються рубрикою «Учимося робити нестандартні кроки». До неї дібрано задачі, для розв’язування яких потрібні не спеціальні алгебраїчні знання, а лише здоровий глузд, винахідливість і кмітливість. Ці задачі корисні, як вітаміни. Вони допоможуть вам навчитися приймати несподівані й нестандартні рішення не тільки в математиці, а й у житті.
Якщо після виконання домашніх завдань залишається вільний час, рекомендуємо звернутися до рубрик «Коли зроблено уроки» та «Для тих, хто хоче знати більше». Матеріал, викладений там, непростий. Але тим цікавіше випробувати свої сили!
Дерзайте! Бажаємо успіху!
Від авторів
ШаноВні коЛеги та коЛежанки!
Ми дуже сподіваємося, що цей підручник стане надійним помічником у вашій нелегкій та шляхетній праці, і будемо щиро раді, якщо він вам сподобається.
У книзі дібрано великий і різноманітний дидактичний матеріал. Проте за один навчальний рік усі задачі розв’язати неможливо, та в цьому й немає потреби. Разом з тим набагато зручніше працювати, коли є значний запас задач. Це дає можливість реалізувати принципи рівневої диференціації та індивідуального підходу в навчанні.
Матеріал рубрики «Коли зроблено уроки» може бути використаний для організації роботи математичного гуртка й факультативних занять.
Бажаємо творчого натхнення та терпіння.
![]()
|
n° |
завдання, що відповідають початковому та середньому рівням навчальних досягнень; |
|
n• |
завдання, що відповідають достатньому рівню навчальних досягнень; |
|
n•• |
завдання, що відповідають високому рівню навчальних досягнень; |
|
n* |
задачі для математичних гуртків і факультативів; |
|
◄ |
закінчення доведення теореми, розв’язування прикладу; |
|
¿ |
завдання, які можна виконувати за допомогою комп’ю тера; |
![]() рубрика «Коли зроблено уроки».
рубрика «Коли зроблено уроки».
Зеленим кольором позначено номери задач, що рекомендуються для домашньої роботи, синім кольором — номери задач, які з урахуванням індивідуальних особливостей учнів класу на розсуд учителя можна розв’язувати усно.
§ 1 НерівНості
•  У цьому параграфі ви дізнаєтеся, у якому випадку число aвважають більшим (меншим), ніж число b; вивчите властивості числових нерівностей; дізнаєтеся, що називають розв’язком нерівності з однією змінною, розв’язком системи нерівностей з однією змінною.
У цьому параграфі ви дізнаєтеся, у якому випадку число aвважають більшим (меншим), ніж число b; вивчите властивості числових нерівностей; дізнаєтеся, що називають розв’язком нерівності з однією змінною, розв’язком системи нерівностей з однією змінною.
• Ви навчитеся оцінювати значення виразів, доводити нерівності, розв’язувати лінійні нерівності та системи лінійних нерівностей з однією змінною.
1. Числові нерівності
На практиці вам часто доводиться порівнювати величини. Наприклад, площа спортивного залу більша за площу класної кімнати, площа України (603,5 тис. км2) більша за площу Франції (551,5 тис. км2), висота гори Роман-Кош (1545 м) менша від висоти гори Говерли (2061 м), відстань від Києва до Харкова (450 км) дорівнює 0,011 довжини екватора.
Результати таких порівнянь можна записувати у вигляді числових нерівностей, використовуючи знаки >, <.
Якщо число a більше за число b, то пишуть: a > b; якщо число a менше від числа b, то пишуть: a < b.
![]() Очевидно, що 12 > 7, –17 < 3,
Очевидно, що 12 > 7, –17 < 3, ![]() , 2 > 1. Справедливість цих нерівностей випливає з правил порівняння дійсних чисел, які ви вивчали в попередніх класах.
, 2 > 1. Справедливість цих нерівностей випливає з правил порівняння дійсних чисел, які ви вивчали в попередніх класах.
Проте числа можна порівнювати не лише за допомогою правил, які було вивчено раніше. Інший спосіб, більш універсальний, заснований на таких очевидних міркуваннях: якщо різниця двох чисел є додатною, то зменшуване більше за від’ємник, якщо ж різниця від’ємна, то зменшуване менше від від’ємника.
Ці міркування підказують, що зручно прийняти таке означення.
Означення. Число a вважають більшим за число b, якщо різниця a – b є додатним числом. Число a вважають меншим від числа b, якщо різниця a – b є від’ємним числом.
Це означення дає змогу задачу про порівняння двох чисел звести до задачі про порівняння їхньої різниці з нулем. Наприклад,
![]() щоби порівняти значення виразів
щоби порівняти значення виразів ![]() і 2 − 3, розглянемо їхню різницю:
і 2 − 3, розглянемо їхню різницю:
![]() Оскільки
Оскільки 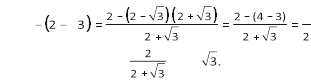
![]() > 0, то > 2 −
> 0, то > 2 −
|
a > b B |
нулю, тому для будь-яких чисел a і b справедли- A ве одне й тільки одне з таких співвідношень: |
|
b a Рис. 1.1 |
a > b, a < b, a = b. Якщо a > b, то точка, яка зображає число a на координатній прямій, лежить праворуч від |
![]() Зауважимо, що різниця чисел a і b може бути або додатною, або від’ємною, або рівною
Зауважимо, що різниця чисел a і b може бути або додатною, або від’ємною, або рівною
точки, яка зображає число b (рис. 1.1). Часто в повсякденному житті ми користуємося висловами «не більше», «не менше». Наприклад, відповідно до санітарних норм кількість учнів у класі має бути не більшою за 30. Дорожній знак, зображений на рисунку 1.2, означає, що швидкість руху автомобіля має бути не меншою від 30 км/год.
 У математиці для вислову «не більше» використо- 30 вують знак m (читають: «менше або дорівнює»), а для
У математиці для вислову «не більше» використо- 30 вують знак m (читають: «менше або дорівнює»), а для
вислову «не менше» — знак l (читають: «більше або
Рис. 1.2
дорівнює»).
Якщо a < b або a = b, то є правильною нерівність a bm .
Якщо a > b або a = b, то є правильною нерівність a bl .
Наприклад, нерівності 7 m7, 7 m15, −3 l −5 є правильними. Зауважимо, що, наприклад, нерівність 7 m5 є неправильною.
Знаки < і > називають знаками строгої нерівності, а знаки m і l називають знаками нестрогої нерівності.
![]() Приклад 1 Доведіть, що при будь-яких значеннях a є правильною нерівність
Приклад 1 Доведіть, що при будь-яких значеннях a є правильною нерівність
(a + 1) (a + 2) > a (a + 3).
Розв’язання. Для розв’язання достатньо показати, що при будь-якому значенні a різниця лівої та правої частин даної нерівності є додатною. Маємо:
(a + 1) (a + 2) – a (a + 3) = a2 + 2a + a + 2 – a2 – 3a = 2. ◄
У таких випадках говорять, що доведено нерівність
(a + 1) (a + 2) > a (a + 3).
![]() Приклад 2 Доведіть нерівність (a – 3)2 < 2a2 – 6a + 10, де a — будь-яке дійсне число.
Приклад 2 Доведіть нерівність (a – 3)2 < 2a2 – 6a + 10, де a — будь-яке дійсне число.
Розв’язання. Розглянемо різницю лівої та правої частин даної нерівності:
(a – 3)2 – (2a2 – 6a + 10) = a2 – 6a + 9 – 2a2 + 6a – 10 = = –a2 – 1 = –a2 + (–1).
При будь-якому значенні a маємо: −a2 m 0. Сума недодатного й від’ємного чисел є число від’ємне. Отже, –a2 + (–1) < 0.
Звідси випливає, що (a – 3)2 < 2a2 – 6a + 10 при будь-якому значенні a. ◄
![]()
![]() Приклад 3 Доведіть нерівність
Приклад 3 Доведіть нерівність ![]() l ab, де al 0, bl 0.
l ab, де al 0, bl 0.
Розв’язання. Розглянемо різницю лівої та правої частин даної нерівності. Маємо:
2 .
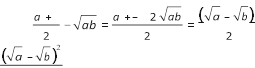 Вираз набуває невід’ємних значень при будь-яких
Вираз набуває невід’ємних значень при будь-яких
2
невід’ємних значеннях змінних a і b. Отже, нерівність, що доводиться, є правильною. ◄
![]() Зауважимо, що вираз ab називають середнім геометричним чисел a і b.
Зауважимо, що вираз ab називають середнім геометричним чисел a і b.
Отже, ми довели, що середнє арифметичне двох невід’ємних чисел не менше від їхнього середнього геометричного.
![]() Приклад 4 Доведіть, що a2 − ab + b2 l 0 при будь-яких значеннях a і b.
Приклад 4 Доведіть, що a2 − ab + b2 l 0 при будь-яких значеннях a і b.
Розв’язання. Маємо:
2
![]()
![]() a2 − ab b+ 2 = a2 − 2æ æa 1 b + 1 b2 + 3 b2 = a − 1 b + 3 b2.
a2 − ab b+ 2 = a2 − 2æ æa 1 b + 1 b2 + 3 b2 = a − 1 b + 3 b2.
2 4 4 2 4
Оскільки a − ![]() 1 b2 l 0 і
1 b2 l 0 і ![]() 3 b2 l 0 при будь-яких значеннях a і b,
3 b2 l 0 при будь-яких значеннях a і b,
2 4
![]() то a − 1 b2 + 3 b2 l 0 при будь-яких значеннях a і b.
то a − 1 b2 + 3 b2 l 0 при будь-яких значеннях a і b.
2 4
Отже, a2 − ab + b2 l 0 при будь-яких значеннях a і b. ◄
1. У якому разі число a вважають більшим за число b?
2. У якому разі число a вважають меншим від числа b?
3.  Як розташована на координатній прямій точка, яка зображає число a, відносно точки, яка зображає число b, якщо a > b?
Як розташована на координатній прямій точка, яка зображає число a, відносно точки, яка зображає число b, якщо a > b?
4. Який символ використовують для вислову «не більше» та як цей символ
читають?
5. Який символ використовують для вислову «не менше» та як цей символ читають?
6. У якому разі є правильною нерівність a bm ?
7. У якому разі є правильною нерівність a bl ?
8. Поясніть, які знаки називають знаками строгої, а які — нестрогої нерівності.
ВПРаВи
1.1.° Порівняйте числа a і b, якщо:
1) a – b = 0,4; 2) a – b = –3; 3) a – b = 0.
1.2.° Відомо, що m < n. Чи може різниця m – n дорівнювати числу:
1) 4,6; 2) –5,2; 3) 0?
1.3.° Яке із чисел, x або y, є більшим, якщо: 1) x – y = –8; 2) y – x = 10?
1.4.° Як розташована на координатній прямій точка A (a) відносно точки B (b), якщо:
1) a – b = 2; 3) a – b = 0;
2) ![]() a – b = –6; 4) b a− = 2?
a – b = –6; 4) b a− = 2?
1.5.° Чи можуть одночасно виконуватися нерівності: 1) a > b і a < b; 2) a bl і a bm ?
1.6.° Порівняйте значення виразів (a – 2)2 і a (a – 4) при значенні a, що дорівнює: 1) 6; 2) –3; 3) 2. Чи можна за результатами виконаних порівнянь стверджувати, що при будь-якому значенні a значення першого виразу більше за відповідне значення другого виразу? Доведіть, що при будь-якому значенні a значення першого виразу більше за відповідне значення другого виразу.
1.7.° Порівняйте значення виразів 4 (b + 1) і b – 2 при значенні b, що дорівнює: 1) –1; 2) 0; 3) 3. Чи можна стверджувати, що при будь-якому значенні b значення виразу 4 (b + 1) більше за відповідне значення виразу b – 2?
1.8.° Доведіть, що при будь-якому значенні змінної є правильною
нерівність:
1) (a + 3) (a + 1) > a (a + 4);
2) 3 (b – 4) + 2b < 5b – 10;
3) (c – 4) (c + 4) > c2 – 20;
4) x (x + 6) – x2 < 2 (3x + 1);
5) (y+ 5)(y− 2) l 3y− 10; 6) 8m2 − 6m + 1 m (3m − 1)2;
7) a a( − 2) l− 1;
8) (b + 7)2 > 14b + 40.
1.9.° Доведіть, що при будь-якому значенні змінної є правильною
нерівність:
1) (p – 3) (p + 4) < p (p + 1); 2) (x + 1)2 > x (x + 2);
3) (a – 5) (a + 2) > (a + 5) (a – 8);
4) y (y + 8) < (y + 4)2; 5) (2a − 5)2 m6a2 − 20a + 25;
6) a2 + 4 l 4a.
1.10.• Чи є правильним твердження:
a a
1) якщо a > b, то > 1; 4) якщо ![]() > 1, то a > b;
> 1, то a > b;
b b
2 2
2) ![]() якщо a > 1, то < 2; 5) якщо a > 1, то a > 1?
якщо a > 1, то < 2; 5) якщо a > 1, то a > 1?
a
2
3) якщо a < 1, то > 2;
a
1.11.• Доведіть нерівність:
1) 2a2 – 8a + 16 > 0;
2) 4b2 + 4b + 3 > 0;
3) a2 + ab + b2 l 0;
4) (3a + 2) (2a – 4) – (2a – 5)2 > 3 (4a – 12);
5) a (a – 3) > 5 (a – 4);
6) (a b a− ) ( + 5b) m (2a b a+ ) ( + 4b) + ab.
1.12.• Доведіть нерівність: 1) 28a − 32 m7a2 − 4;
2) 9x2 − 6xy + 4y2 l 0;
3) 3 (b – 1) < b (b + 1);
4) (4p – 1) (p + 1) – (p – 3) (p + 3) > 3 (p2 + p).
1.13.• Доведіть, що:
1) a3 − 6a2 + a − 6 l 0, якщо al 6;
2) ab + 1 > a + b, якщо a > 1 і b > 1;
3) ![]() a+ 3 + 3a− 2 < a, якщо a < –6.
a+ 3 + 3a− 2 < a, якщо a < –6.
3 4
1.14.• Доведіть, що:
1) ab b( − a) ma3 − b3, якщо a bl ;
2) ![]() a− 1 − a− 2 > 1, якщо a > 2.
a− 1 − a− 2 > 1, якщо a > 2.
2 3 2
1.15.• Порівняйте суму квадратів двох довільних чисел та їхній подвоєний добуток.
1.16.• Дано три послідовних натуральних числа. Порівняйте:
1) квадрат середнього із цих чисел і добуток двох інших;
2) подвоєний квадрат середнього із цих чисел і суму квадратів двох інших.
1.17.• Порівняйте суму квадратів двох додатних чисел і квадрат їхньої суми.
1.18.• Як зміниться — збільшиться чи зменшиться — правильний a
дріб ![]() , де a > 0, b > 0, якщо його чисельник і знаменник збільb
, де a > 0, b > 0, якщо його чисельник і знаменник збільb
шити на одне й те саме число?
1.19.• Як зміниться — збільшиться чи зменшиться — неправильний a
дріб ![]() , де a > 0, b > 0, якщо його чисельник і знаменник збільb
, де a > 0, b > 0, якщо його чисельник і знаменник збільb
шити на одне й те саме число?
1.20.• Доведіть, що сума будь-яких двох взаємно обернених додатних чисел не менша від 2.
1.21.• Доведіть, що сума будь-яких двох взаємно обернених від’ємних чисел не більша за –2.
1.22.• Чи є правильною дана нерівність при будь-яких значеннях a і b:
a2 −b2 a2 −b2
1) ![]() 2 + 1 > 1; 2)
2 + 1 > 1; 2) ![]() b2 + 1 > −1?
b2 + 1 > −1?
a
1.23.• Доведіть, що при всіх значеннях змінної є правильною нерівність:
|
a2 1
|
(5a + 1)2 2) 5 |
1.24.• Доведіть, що коли a < b, то a < ![]() < b.
< b.
1. 25.•• Доведіть, що коли a < b < c, то a < ![]() < c.
< c.
2
![]() •• a + 4 2 3 при всіх зна-
•• a + 4 2 3 при всіх зна-
1.26. Чи є правильною нерівність l a +
2
ченнях a?
1.27.•• Доведіть, що при всіх значеннях змінної є правильною неa2 + 2 рівність l 2.
2
![]() a + 1
a + 1
1.28.•• Доведіть нерівність:
1) a2 + b2 + 6a − 4b + 13 l 0;
2) x2 – 2x + y2 + 10y + 28 > 0;
3) 2m2 − 6mn + 9n2 − 6m + 9 l 0; 4) a2 + b2 + c2 + 12 l 4 (a b c+ + ); 5) a b2 2 + a2 + b2 + 1l 4ab.
1. 29.•• Доведіть нерівність:
1) a2 + b2 – 16a + 14b + 114 > 0;
2) x2 + y2 + 10 l 6x − 2y; 3) c2 + 5d2 + 4cd − 4d + 4 l 0.
![]()
1.30. Відомо, що a > 0, b > 0, c < 0, d < 0. Порівняйте з нулем значення виразу:
a ac
1) ![]()
![]() bc; 3) ; 5) ; 7) abcd; b d
bc; 3) ; 5) ; 7) abcd; b d
ab a b
2) cd; 4) ; 6) ; 8) ![]() . c bc acd
. c bc acd
1.31. Що можна сказати про знаки чисел a і b, якщо: a 2
1) ab > 0; 3) > 0; 5) a b > 0;
b
![]() a 2
a 2
2) ab < 0; 4) < 0; 6) a b < 0?
b
1.32. Поясніть, чому при будь-яких значеннях змінної (чи змінних) є правильною нерівність:
1) a2 l 0; 5) a2 + b2 l 0;
2) a2 + 1 > 0; 6) a2 + b2 + 2 > 0;
3) ![]() (a + 1)2 l 0; 7) (a − 2)2 + (b + 1)2 l 0; 4) a2 − 4a + 4 l 0; 8) a2 + 3 > 0.
(a + 1)2 l 0; 7) (a − 2)2 + (b + 1)2 l 0; 4) a2 − 4a + 4 l 0; 8) a2 + 3 > 0.
1.33. Порівняйте з нулем значення виразу, де a — довільне число:
1) 4 + a2; 4) –4 – (a – 4)2; 2) (4 – a)2; 5) (–4)8 + (a – 8)4; 3) –4 – a2; 6) (4 – a)2 + (4a – 1000)2.
1.34. Спростіть вираз:
1) 2a (5a – 7) – 5a (3 – 2a);
2) (2b – 3) (4b + 9);
3) (2c – 6) (8c + 5) – (5c + 2) (5c – 2);
4) 16m2 – (3 – 4m) (3 + 4m);
5) (2x – 1)2 + (2x + 1)2; 6) (x – 4) (x + 4) – (x – 8)2.
 УЧиМоСЯ Робити неСтандаРтні кРоки
УЧиМоСЯ Робити неСтандаРтні кРоки
1.35. Усі натуральні числа від 1 до 1000 включно розбили на дві групи: парні числа та непарні числа. У якій із груп сума всіх цифр, використаних для запису чисел, є більшою та на скільки?
 2. основні властивості числових нерівностей
2. основні властивості числових нерівностей
У цьому пункті розглянемо властивості числових нерівностей, які часто використовують під час розв’язування задач. Їх називають основними властивостями числових нерівностей.
Теорема 2.1. Якщо a > b і b > c, то a > c.
Доведення. Оскільки за умовою a > b і b > c, то різниці a – b і b – c є додатними числами. Тоді додатною буде їхня сума
(a – b) + (b – c). Маємо: (a – b) + (b – c) = a – c. Отже, різниця a – c є додатним числом, тому a > c. ◄
Аналогічно можна довести таку властивість: якщо a < b і b < c, то a < c.
2. основні властивості числових нерівностей
|
трично (рис. 2.1): якщо на координатній прямій точка A (a) лежить праворуч від точки B (b), а точка B (b) — праворуч від точки C (c), то точка A (a) лежить праворуч від точки C (c). |
c |
b a Рис. 2.1 |
![]() Теорему 2.1 можна проілюструвати геоме- C B A
Теорему 2.1 можна проілюструвати геоме- C B A
Теорема 2.2. Якщо a > b і c — будь-яке число, то a +c > b +c.
Доведення. Розглянемо різницю (a + c) – (b + c). Маємо: (a + c) – (b + c) = a – b. Оскільки за умовою a > b, то різниця a – b є додатним числом. Отже, a + c > b + c. ◄
Аналогічно можна довести таку властивість: якщо a < b і c — будь-яке число, то a + c < b + c.
Оскільки віднімання можна замінити додаванням (a – c =
= a + (–c)), то теорему 2.2 можна сформулювати так:
якщо до обох частин правильної нерівності додати або від обох частин правильної нерівності відняти одне й те саме число, то отримаємо правильну нерівність.
Наслідок. Якщо будь-який доданок перенести з однієї частини правильної нерівності в другу, замінивши знак доданка на протилежний, то отримаємо правильну нерівність.
Доведення. Нехай нерівність a > b + c є правильною. Віднімемо від обох її частин число c. Отримаємо: a – c > b + c – c, тобто a – с > b. ◄
Теорема 2.3. Якщо a > b і c — додатне число, то ac > bc. Якщо a > b і c — від’ємне число, то ac < bc.
Доведення. Розглянемо різницю ac – bc. Маємо: ac – bc = c (a – b).
За умовою a > b, отже, різниця a – b є додатним числом.
Якщо c > 0, то добуток c (a – b) є додатним числом, отже, різниця ac – bc є додатною, тобто ac > bc.
Якщо c < 0, то добуток c (a – b) є від’ємним числом, отже, різниця ac – bc є від’ємною, тобто ac < bc. ◄
Аналогічно можна довести таку властивість: якщо a < b і c — додатне число, то ac <bc. Якщо a < b і c — від’ємне число, то ac > bc.
![]() a = aæ1 , то
a = aæ1 , то
Оскільки ділення можна замінити множенням
c c
теорему 2.3 можна сформулювати так:
якщо обидві частини правильної нерівності помножити або
поділити на одне й те саме додатне число, то отримаємо правильну нерівність;
якщо обидві частини правильної нерівності помножити або
поділити на одне й те саме від’ємне число та замінити знак нерівності на протилежний, то отримаємо правильну нерівність.
1 1
![]() Наслідок. Якщо ab > 0 і a > b, то < .
Наслідок. Якщо ab > 0 і a > b, то < .
a b
Доведення. Поділимо обидві частини нерівності a > b на до-
a b
![]() датне число ab. Отримаємо правильну нерівність > , тобто ab ab
датне число ab. Отримаємо правильну нерівність > , тобто ab ab
1 1 1 1
![]()
![]() > . Звідси < . ◄ b a a b
> . Звідси < . ◄ b a a b
Звернемо увагу, що коли з формулювання наслідку вилучити умову ab > 0, тобто вимогу, щоб числа a і b мали однакові знаки,
1 1
то з нерівності a > b може не випливати нерівність < . Дійсно,
a b
![]() нерівність 5 > –3 є правильною, проте нерівність 1 < − 1 є непра-
нерівність 5 > –3 є правильною, проте нерівність 1 < − 1 є непра-
5 3
вильною.
У теоремах цього пункту йшлося про строгі нерівності. Аналогічні властивості притаманні й нестрогим нерівностям. Наприклад, якщо a bl і c — будь-яке число, то a c b+ l + c.
1. Яке із чисел — a або c — більше, якщо відомо, що a > b і b > c?
2. сформулюйте теорему про додавання до обох частин нерівності одного й того самого числа.
3. сформулюйте наслідок із теореми про додавання до обох частин нерівності одного й того самого числа.
4.  сформулюйте теорему про множення обох частин нерівності на одне й те саме число.
сформулюйте теорему про множення обох частин нерівності на одне й те саме число.
5. сформулюйте наслідок із теореми про множення обох частин нерівності на одне й те саме число.
ВПРаВи
2.1.° Відомо, що a > 6. Чи є правильною нерівність:
1) a > 4; 2) al 5,9; 3) a > 7?
2.2.° Відомо, що a < b і b < c. Яке з тверджень є правильним:
1) a > c; 2) a = c; 3) c > a?
2. основні властивості числових нерівностей
2.3.° Запишіть нерівність, яку отримаємо, якщо:
1) до обох частин нерівності –3 < 4 додамо число 5; число –2;
2) від обох частин нерівності –10 < –6 віднімемо число 3; число –4;
3) обидві частини нерівності 7 > –2 помножимо на число 5; на число –1;
4) обидві частини нерівності 12 < 18 поділимо на число 6; на число –2.
2.4.° Відомо, що a > b. Запишіть нерівність, яку отримаємо, якщо:
1) до обох частин даної нерівності додамо число 8;
2) від обох частин даної нерівності віднімемо число –6;
3) обидві частини даної нерівності помножимо на число 12;
4) обидві частини даної нерівності помножимо на число −![]() ;
;
5) обидві частини даної нерівності поділимо на число ![]() ;
;
6) обидві частини даної нерівності поділимо на число –4.
2.5.• Відомо, що b > a, c < a і d > b. Порівняйте числа: 1) a і d; 2) b і c.
2.6.• Розташуйте в порядку зростання числа a, b, c і 0, якщо a > b, 0 < b і 0 > c.
2.7.• Відомо, що a > 4. Порівняйте з нулем значення виразу:
1) a – 3; 3) (a – 3) (a – 2); 5) (1 – a)2 (4 – a).
2) 2 – a; 4) ![]() (a − 4) (a − 2);
(a − 4) (a − 2);
3 − a
2.8.• Відомо, що –2 < b < 1. Порівняйте з нулем значення виразу:
1) b + 2; 3) b – 2; 5) (b + 2) (b – 4)2;
2) 1 – b; 4) (b – 1) (b – 3); 6) (b – 3) (b + 3) (b – 2)2.
2.9.• Дано: a > b. Порівняйте:
1) a + 9 і b + 9; 5) –40b і –40a;
a b
2) ![]() b – 6 і a – 6; 6) і ;
b – 6 і a – 6; 6) і ;
20 20
3) 1,8a і 1,8b; 7) 2a – 3 і 2b – 3; 4) –a і –b; 8) 5 – 8a і 5 – 8b.
2.10.• Відомо, що 1 mm < 2. Які з нерівностей є правильними:
1) −1 m− m < −2; 3) −1l − m > −2;
2) −2 < −mm− 1; 4) −2 > −ml − 1?
2.11.• Дано: –3a > –3b. Порівняйте:
1) a і b; 4) −![]() b і −
b і −![]() a;
a;
2) ![]() a і
a і ![]() b; 5) 3a + 2 і 3b + 2;
b; 5) 3a + 2 і 3b + 2;
3) b – 4 і a – 4; 6) –5a + 10 і –5b + 10.
2.12.• Відомо, що a > b. Розташуйте в порядку спадання числа a + 7, b – 3, a + 4, b – 2, b.
2.13.• Дано: a < b. Порівняйте:
1) a – 5 і b; 2) a і b + 6; 3) a + 3 і b – 2.
2.14.• Порівняйте числа a і b, коли відомо, що: 1) a > c і c > b + 3; 2) a > c і c – 1 > b + d2, де c і d — деякі числа.
2.15.• Порівняйте числа a і 0, якщо:
1) 7a < 8a; 3) –6a > –8a; a a
2) ![]() < ; 4) –0,02a > –0,2a.
< ; 4) –0,02a > –0,2a.
2 3
2.16.• Дано: a > –2. Доведіть, що:
1) 7a + 10 > –4; 2) –6a – 3 < 10.
2.17.• Дано: bm10. Доведіть, що:
1) 5b − 9 m 41; 2) 1 – 2b > –21.
2.18.• Чи є правильним твердження:
1) якщо a > b, то a > –b;
2) якщо a > b, то 2a > b;
3) якщо a > b, то 2a + 1 > 2b;
4) якщо a > b + 2 і b – 3 > 4, то a > 9;
5) якщо a > b, то ab > b2;
6) оскільки 5 > 3, то 5a2 > 3a2;
7) оскільки 5 > 3, то 5 (a2 + 1) > 3 (a2 + 1)?
2.19.•• Запишіть нерівність, яку отримаємо, якщо:
1) обидві частини правильної нерівності a > 2 помножимо на a; 2) обидві частини правильної нерівності b < –1 помножимо на b;
3) обидві частини правильної нерівності m < –3 помножимо на –m;
4) обидві частини правильної нерівності c > –4 помножимо на c.
2. 20.•• Запишіть нерівність, яку отримаємо, якщо:
1) обидві частини правильної нерівності a < –a2 поділимо на a; 2) обидві частини правильної нерівності a > 2a2 поділимо на a;
3) обидві частини правильної нерівності a3 > a2 поділимо на –a.
![]()
2.21. Відомо, що a2 + b2 = 18 і (a + b)2 = 20. Чому дорівнює значення виразу ab?
2.22. У Дмитра у 2 рази більше марок, ніж у Надії, у Надії — у 2 рази більше марок, ніж у Михайла. Якому з наведених чисел може дорівнювати кількість марок, що має Дмитро?
1) 18; 2) 22; 3) 24; 4) 30.
2.23. Спростіть вираз:
|
a2 + b2 b 1) 2 + ;
2) 2 − 9 − a+ 3; a |
c+ 1 c2 − 1 3) : 2 ; 3c 6c
4) 2 −n2 : (m n+ ). m |
2.24. Моторний човен за один і той самий час може проплисти 48 км за течією річки або 36 км проти течії. Яка власна швидкість човна, якщо швидкість течії становить 2 км/год?
 3. додавання і множення числових нерівностей. оцінювання значення виразу
3. додавання і множення числових нерівностей. оцінювання значення виразу
Розглянемо приклади.
1) Якщо з першого поля зібрали не менше ніж 40 т жита, а з другого поля — не менше ніж 45 т, то очевидно, що з двох полів разом зібрали не менше ніж 85 т жита.
2) Якщо довжина прямокутника не більша за 70 см, а ширина — не більша за 40 см, то зрозуміло, що його площа не більша за 2800 см2.
Висновки із цих прикладів є інтуїтивно очевидними. Їхню правильність підтверджують такі теореми.
Теорема 3.1 (про почленне додавання нерівностей).
Якщо a >b і c > d, то a +c > b +d.
Доведення. Розглянемо різницю (a + c) – (b + d). Маємо:
(a + c) – (b + d) = a + c – b – d = (a – b) + (c – d).
Оскільки a > b і c > d, то різниці a – b і c – d є додатними числами. Отже, різниця, що розглядається, є додатною, тобто a + c > b + d. ◄
Аналогічно можна довести таку властивість: якщо a < b і c < d, то a + c < b + d.
Нерівності a > b і c > d (або a < b і c < d) називають нерівностями однакового знака, а нерівності a > b і c < d (або a < b і c > d) — нерівностями протилежних знаків.
Говорять, що нерівність a + c > b + d отримано з нерівностей a > b і c > d шляхом почленного додавання.
Теорема 3.1 означає, що при почленному додаванні правильних нерівностей однакового знака результатом є правильна нерівність того самого знака.
Зазначимо, що теорема 3.1 справедлива й у разі почленного додавання трьох і більше нерівностей. Наприклад, якщо a1 > b1, a2 > b2 і a3 > b3, то a1 + a2 + a3 > b1 + b2 + b3.
Теорема 3.2 (про почленне множення нерівностей).
Якщо a > b, c > d і a, b, c, d — додатні числа, то ac > bd.
Доведення. Розглянемо різницю ac – bd. Маємо: ac – bd = ac – bc + bc – bd = c (a – b) + b (c – d).
За умовою a – b > 0, c – d > 0, c > 0, b > 0. Отже, різниця, що розглядається, є додатною. Із цього випливає, що ac > bd. ◄
Аналогічно можна довести властивість: якщо a < b, c < d і a, b, c, d — додатні числа, то ac < bd.
Говорять, що нерівність ac > bd отримано з нерівностей a > b і c > d шляхом почленного множення.
Теорема 3.2 означає, що при почленному множенні правильних нерівностей однакового знака, у яких ліві та праві частини — додатні числа, результатом є правильна нерівність того самого знака.
Звернемо увагу: якщо з формулювання теореми 3.2 вилучити вимогу, щоб a, b, c, d були додатними числами, то з нерівностей a > b і c > d може не випливати нерівність ac > bd. Справді, розглянемо дві правильні нерівності –2 > –3 і 4 > 1. Помноживши почленно ці нерівності, отримаємо неправильну нерівність –8 > –3.
Зауважимо, що теорема 3.2 справедлива й у разі почленного множення трьох і більше нерівностей. Наприклад, якщо a1, a2, a3, b1, b2, b3 — додатні числа, причому a1 > b1, a2 > b2, a3 > b3, то a1a2a3 > b1b2b3.
Наслідок. Якщо a > b і a, b — додатні числа, то an > bn, де n — натуральне число.
Доведення. Запишемо n правильних нерівностей a > b: a b> a b>
n нерівностей
... a b>
Оскільки a і b — додатні числа, то можемо перемножити почленно n записаних нерівностей. Отримаємо: an > bn. ◄
Зазначимо, що всі розглянуті властивості нерівностей є правильними й у тому випадку, коли нерівності є нестрогими:
якщо a bl і c dl , то a c b d+ l + ; якщо a bl , c dl і a, b, c, d — додатні числа, то ac bdl ; якщо a bl і a, b — додатні числа, то an lbn,де n — нату-
ральне число.
Ви знаєте, що значення величин, які є результатом вимірювань, не є точними. Вимірювальні прилади дають змогу лише встановити, між якими числами знаходиться точне значення величини. Ці числа називають межами значення величини.
Нехай, наприклад, у результаті вимірювання ширини x і довжини y прямокутника було встановлено, що 2,5 см < x < 2,7 см і 4,1 см < y < 4,3 см. Тоді за допомогою теореми 3.2 можна оцінити площу прямокутника. Маємо:
2,5 см < x < 2,7 см
×
4,1 см < y < 4,3 см
![]()
10,25 см2 < xy < 11,61 см2.
Узагалі, якщо відомо значення меж величин, то, використовуючи властивості числових нерівностей, можна знайти межі значення виразу, який містить ці величини, тобто оцінити його значення.
![]() Приклад 1 Дано: 6 < a < 8 і 10 < b < 12. Оцініть значення ви
Приклад 1 Дано: 6 < a < 8 і 10 < b < 12. Оцініть значення ви
разу:
a 1
1) a + b; 2) a – b; 3) ab; 4) ![]() ; 5) 3a−
; 5) 3a− ![]() b. b 2
b. b 2
Розв’язання. 1) Застосувавши теорему про почленне додавання нерівностей, отримуємо:
6 < a < 8
+ 10 < b < 12
![]()
16 < a + b < 20.
2) Помноживши кожну частину нерівності 10 < b < 12 на –1, отримуємо: –10 > –b > –12, тобто –12 < –b < –10. Ураховуючи, що a – b = a + (–b), далі маємо:
6 < a < 8
+ –12 < –b < –10
![]()
–6 < a – b < –2.
3) Оскільки a > 6 і b > 10, то a і b набувають додатних значень. Застосувавши теорему про почленне множення нерівностей, отримуємо:
6 < a < 8
×
10 < b < 12
![]()
60 < ab < 96.
1 1 1 1 1 1
4) ![]()
![]() Оскільки 10 < b < 12, то > > , тобто < < . Ура-
Оскільки 10 < b < 12, то > > , тобто < < . Ура-
10 b 12 12 b 10
a 1
![]() ховуючи, що = aæ , маємо: b b
ховуючи, що = aæ , маємо: b b
6 < a < 8
×
1 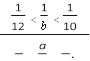 4
4
< <
2 b 5
5) Помножимо кожну частину нерівності 6 < a < 8 на 3, а кожну частину нерівності 10 < b < 12 на −![]() .
.
Отримуємо дві правильні нерівності:
18 < 3a < 24 і −5 > −![]() b > −6.
b > −6.
Додамо отримані нерівності:
18 < 3a < 24
![]() +
+
−6 < −b < −5
![]()
12 < 3a − ![]() b < 19.
b < 19.
Відповідь: 1) 16 < a + b < 20; 2) –6 < a – b < –2; 3) 60 < ab < 96;
1 a 4 1
![]() 4) < < ; 5) 12 < 3a −
4) < < ; 5) 12 < 3a − ![]() b < 19. ◄
b < 19. ◄
2 b 5 2
![]() Приклад 2 Доведіть, що 24 + 47 < 12.
Приклад 2 Доведіть, що 24 + 47 < 12.
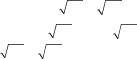 Розв’язання. Оскільки 24 < 5 і 47 < 7, то 24 + 47 < 5 + 7 = 12. ◄
Розв’язання. Оскільки 24 < 5 і 47 < 7, то 24 + 47 < 5 + 7 = 12. ◄
1. сформулюйте теорему про почленне додавання нерівностей.
2.  Поясніть, які нерівності називають нерівностями однакового знака, а які — нерівностями протилежних знаків.
Поясніть, які нерівності називають нерівностями однакового знака, а які — нерівностями протилежних знаків.
3. сформулюйте теорему про почленне множення нерівностей.
4. сформулюйте наслідок з теореми про почленне множення нерівностей.
![]()
3.1.° Запишіть нерівність, яку отримаємо, якщо:
1) додамо почленно нерівності 10 > –6 і 8 > 5;
2) перемножимо почленно нерівності 2 < 7 і 3 < 4;
3) перемножимо почленно нерівності 1,2 > 0,9 і 5 > ![]() .
.
3.2.° Запишіть нерівність, яку отримаємо, якщо:
1) додамо почленно нерівності –9 < –4 і –6 < 4;
2) перемножимо почленно нерівності ![]() і 24 < 27.
і 24 < 27.
3.3.° Дано: –3 < a < 4. Оцініть значення виразу:
1) 2a; 3) a + 2; 5) 3a + 1; 7) –4a; a
2) ![]() ; 4) a – 1; 6) –a; 8) –5a + 3.
; 4) a – 1; 6) –a; 8) –5a + 3.
3
3.4.° Дано: 2 < b < 6. Оцініть значення виразу:
1) ![]() b; 2) b – 6; 3) 2b + 5; 4) 4 – b.
b; 2) b – 6; 3) 2b + 5; 4) 4 – b.
![]() 3.5.° Відомо, що 2,6 < 7 < 2,7. Оцініть значення виразу:
3.5.° Відомо, що 2,6 < 7 < 2,7. Оцініть значення виразу:
![]()
![]()
![]() 1) 3 7; 2) −2 7; 3) 7 + 1 3, ; 4) 0,1 7 + 0,3.
1) 3 7; 2) −2 7; 3) 7 + 1 3, ; 4) 0,1 7 + 0,3.
3.6.° Дано: 5 < a < 6 і 4 < b < 7. Оцініть значення виразу:
1) a + b; 2) ab; 3) a – b.

![]() 3.7.° Відомо, що 2,2 < 5 < 2,3 і 1,7 < 3 < 1,8. Оцініть значення
3.7.° Відомо, що 2,2 < 5 < 2,3 і 1,7 < 3 < 1,8. Оцініть значення
виразу:
![]()
![]() 1) 5 + 3; 2) 5 − 3; 3) 15.
1) 5 + 3; 2) 5 − 3; 3) 15.
1
3.8.° Дано: 2 < x < 4. Оцініть значення виразу .
x
3.9.° Оцініть середнє арифметичне значень a і b, якщо відомо, що 2,5 < a < 2,6 і 3,1 < b < 3,2.
3.10.° Оцініть периметр рівнобедреного трикутника з основою a см і бічною стороною b см, якщо 10 < a < 14 і 12 < b < 18.
3.11.° Оцініть периметр паралелограма зі сторонами a см і b см, якщо 15 m ma 19 і 6 m mb 11.
3.12.• Чи є правильним твердження: 1) якщо a > 2 і b > 7, то a + b > 9; 2) якщо a > 2 і b > 7, то a + b > 8;
3) якщо a > 2 і b > 7, то a + b > 9,2;
4) якщо a > 2 і b > 7, то a – b > –5;
5) якщо a > 2 і b > 7, то b – a > 5;
6) якщо a > 2 і b > 7, то ab > 13;
7) якщо a > 2 і b > 7, то 3a + 2b > 20;
8) якщо a > 2 і b < –7, то a – b > 9;
9) якщо a < 2 і b < 7, то ab < 14;
10) якщо a > 2, то a2 > 4;
11) якщо a < 2, то a2 < 4;
12) 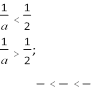 якщо a > 2, то ;
якщо a > 2, то ;
13) якщо a < 2, то
14) якщо –3 < a < 3, то − 1 1 1?
3 a 3
3.13.• Дано: a > 2,4 і b > 1,6. Порівняйте:
1) a + ![]() b і 3,6; 3) (a – 0,4) (b + 1,4) і 6.
b і 3,6; 3) (a – 0,4) (b + 1,4) і 6.
2) (a + b)2 і 16;
3.14.• Відомо, що a > 3 і b > –2. Доведіть, що 5a + 4b > 7.
3.15.• Відомо, що a > 5 і b < 2. Доведіть, що 6a – 7b > 16.
3. 16.• Дано: 5 < a < 8 і 3 < b < 6. Оцініть значення виразу: a 2b
1) 4a + 3b; 2) 3a – 6b; 3) ![]() ; 4)
; 4) ![]() .
.
b 3a
![]()
![]() •1 1
•1 1
![]() 3.17. Дано: < x < і < y <. Оцініть значення виразу:
3.17. Дано: < x < і < y <. Оцініть значення виразу:
2 7
y
1) 6x + 14y; 2) 28y – 12x; 3) ![]() . x
. x
3.18.• Порівняйте значення виразів:
1) 224 і 98; 2) 0,320 і 0,110; 3) 0,001510 і 0,240.
3.19.• Доведіть, що периметр чотирикутника більший за суму його діагоналей.
3.20.• Доведіть, що кожна діагональ опуклого чотирикутника менша від його півпериметра.
3.21.• Доведіть, що сума двох протилежних сторін опуклого чотирикутника менша від суми його діагоналей.
3. 22.• Доведіть твердження:
1) якщо a < b < 0, то a2 > b2;
2) якщо a > 0, b > 0 і a2 > b2, то a > b.
• 1 1
![]() 3.23. Доведіть, що коли a < b < 0, то > .
3.23. Доведіть, що коли a < b < 0, то > .
a b
3. 24.• Відомо, що b > 0 і a > b. Чи є правильною при всіх указаних значеннях a і b нерівність:

3.29. Спростіть вираз: x− 3 x2
1) ![]() æx + ; x+ 3 3 −x
æx + ; x+ 3 3 −x
![]() a ba b+− − a ba b+− : a2ab−b2 . 2)
a ba b+− − a ba b+− : a2ab−b2 . 2)
3.30. Спростіть вираз:
2
1) ![]() 6 3 + 27 − 3 75; 3) (2 − 3 ) .
6 3 + 27 − 3 75; 3) (2 − 3 ) .
2) ![]() ( 50 − 3 2 ) 2;
( 50 − 3 2 ) 2;
3.31. При яких значеннях змінної має зміст вираз:
![]() x2 x − 4 x2 − 4 4 1 1)
x2 x − 4 x2 − 4 4 1 1) ![]() x ; 2)
x ; 2) ![]() 2 ; 3)
2 ; 3) ![]() x2 + 4; 4) x− 4 + x ?
x2 + 4; 4) x− 4 + x ?
+ 4 x − 4
3.32. ![]() У саду ростуть яблуні та вишні, причому вишні становлять 20 % усіх дерев. Скільки відсотків становить кількість яблунь від кількості вишень? готУЄМоСЯ до ВиВЧеннЯ ноВоЇ теМи
У саду ростуть яблуні та вишні, причому вишні становлять 20 % усіх дерев. Скільки відсотків становить кількість яблунь від кількості вишень? готУЄМоСЯ до ВиВЧеннЯ ноВоЇ теМи
3.33. Чи є рівносильними рівняння:
1) 4x + 6 = 2x – 3 і 4x + 3 = 2x – 6;
2) 8x – 4 = 0 і 2x – 1 = 0;
3) x2 + 2x – 3 = 0 і x2 + x = 3 – x; x2 − 1 2
4) ![]() = 0 і x – 1 = 0; x+ 1
= 0 і x – 1 = 0; x+ 1
x2 − 1
5) = 0 і x – 1 = 0; x+ 1
6) x2 + 1 = 0 і 0x = 5?
 УЧиМоСЯ Робити неСтандаРтні кРоки
УЧиМоСЯ Робити неСтандаРтні кРоки
![]() 3.34. Доведіть, що для непарних чисел a, b, c, d, e і f не може виконуватися рівність 1 + 1 + 1 + 1 + 1 + 1 = 1.
3.34. Доведіть, що для непарних чисел a, b, c, d, e і f не може виконуватися рівність 1 + 1 + 1 + 1 + 1 + 1 = 1.
a b c d e f
 Про деякі способи доведення нерівностей
Про деякі способи доведення нерівностей
У п. 1 було доведено кілька нерівностей. Ми використовували такий прийом: розглядали різницю лівої і правої частин нерівності та порівнювали її з нулем.
Проте існує і ряд інших способів доведення нерівностей. Ознайомимося з деякими з них.
Про деякі способи доведення нерівностей
Міркування «від супротивного» Назва цього методу відображає його сутність.
![]() Приклад 1 Для будь-яких чисел a1, a2, b1, b2 доведіть нерівність
Приклад 1 Для будь-яких чисел a1, a2, b1, b2 доведіть нерівність
(ab1 1 + a b2 2)2 m(a12 + a22)(b12 + b22). (*)
Розв’язання. Припустимо, що нерівність, яку доводимо, є неправильною. Тоді знайдуться такі числа a1, a2, b1, b2, що буде правильною нерівність
(ab1 1 + a b2 2)2 > (a12 + a22)(b12 + b22).
Звідси
a b12 12 + 2a1 1 2 2ba b + a b22 22 > a b12 12 + a b12 22 + a b22 12 + a b22 22;
2aba b1 1 2 2 > a b12 22 + a b22 12; a b12 22 − 2aba b1 1 2 2 + a b22 12 < 0;
(a1b2 – a2b1)2 < 0.
Остання нерівність є неправильною. Отримана суперечність означає, що нерівність (*) є правильною. ◄
Нерівність (*) є окремим випадком більш загальної нерівності
(ab1 1 + a b2 2 + ... + a bn n )2 m(a12 + a22 + ... + an2)(b12 + b22 + ... + bn2). (**)
Нерівність (**) називають нерівністю Коші—Буняковського. З її доведенням ви можете ознайомитися на заняттях математичного гуртка.
Метод використання очевидних нерівностей
![]() Приклад 2 Для будь-яких чисел a, b і c доведіть нерівність
Приклад 2 Для будь-яких чисел a, b і c доведіть нерівність
a2 + b2 + c2 lab bc ac+ + .
 Огюстен Луї Коші
Огюстен Луї Коші
(1789–1857)
Видатний французький математик, автор понад 800 наукових праць.
Розв’язання. Очевидно, що при будь-яких значеннях a, b і c виконується така нерівність:
(a b− )2 + (b c− )2 + (c a− )2 l 0.
Звідси отримуємо: a2 − 2ab + b2 + b2 − 2bc c+ 2 + c2 − 2ac a+ 2 l 0;
2a2 + 2b2 + 2c2 l 2ab + 2bc + 2ac; a2 + b2 + c2 lab bc ac+ + . ◄
Метод застосування раніше доведеної нерівності
У п. 1 ми довели, що для будь-яких al0 і bl0 є правильною нерівність
![]()
![]() l ab.
l ab.
Її називають нерівністю Коші для двох чисел.
Розглянемо, як можна використовувати нерівність Коші під час доведення інших нерівностей.
![]() Приклад 3 Доведіть, що для додатних чисел a і b справедлива нерівність
Приклад 3 Доведіть, що для додатних чисел a і b справедлива нерівність
![]() a + 1 b + 1 l 4.
a + 1 b + 1 l 4.
b a
Розв’язання. Застосуємо нерівність Коші для додатних чисел
1
a і ![]() . Отримуємо: b
. Отримуємо: b
1
a +
b ![]() l aæ1.
l aæ1.
2 b
1 a
![]() Звідси a + l 2 . b b
Звідси a + l 2 . b b
1 b
![]() Аналогічно можна довести, що b + l 2 .
Аналогічно можна довести, що b + l 2 .
a a
 Віктор Якович
Віктор Якович
Буняковський
(1804–1889)
Видатний математик ХІХ ст.
Народився на Вінниччині. Протягом багатьох років був віце-президентом Петербурзької академії наук.
Про деякі способи доведення нерівностей
Застосувавши теорему про почленне множення нерівностей, отримаємо:
 a + 1 b + 1 l 4 aæ b .
a + 1 b + 1 l 4 aæ b .
b a b a
Звідси a + 1 b + 1 l 4. ◄
b a
![]() Метод геометричної інтерпретації Приклад 4 Доведіть нерівність:
Метод геометричної інтерпретації Приклад 4 Доведіть нерівність:
99æ101 + 98æ102 + ... + 2æ198 + 1 199æ < ![]() .
.
Розв’язання. Розглянемо чверть кола радіуса 1 із центром O. Впишемо в неї ступінчасту фігуру, яка складається з 99 прямокутників, так, як показано на рисунку 3.1. Маємо:
 99æ101 1æ199 A98 A99
99æ101 1æ199 A98 A99
Звідси випливає нерівність, що до- Рис. 3.1 водиться. ◄
![]()
![]() 1. Доведіть нерівність: 1) (a b+ ) 1 + 1 l 4, якщо a > 0 і b > 0;
1. Доведіть нерівність: 1) (a b+ ) 1 + 1 l 4, якщо a > 0 і b > 0;
a b
2) (a b b c a c+ ) ( + ) ( + ) l 8abc, якщо al 0, bl0 і cl 0;
3) (a3 + b a b) ( + 3) l 4a b2 2, якщо al0 і bl 0;
4) (ab + 1) (a b+ ) l 4ab, якщо al0 і bl 0;
5) ![]() (a + 2) (b + 5) (c + 10) l 80 abc, якщо al 0, bl0 і cl 0;
(a + 2) (b + 5) (c + 10) l 80 abc, якщо al 0, bl0 і cl 0;
1 1
6) ![]() a b+ + + l 4, якщо a>0 і b> 0; a b
a b+ + + l 4, якщо a>0 і b> 0; a b
7) (1 + a1) (1 + a2) ... (1 + an) l 2n, якщо a1, a2, ..., an — додатні числа, добуток яких дорівнює 1.
 4. нерівності з однією змінною
4. нерівності з однією змінною
Розглянемо задачу. Одна зі сторін паралелограма дорівнює 7 см. Якою має бути довжина сусідньої сторони, щоби периметр паралелограма був більшим за 44 см?
Нехай шукана сторона дорівнює x см. Тоді периметр паралелограма дорівнює (14 + 2x) см. Нерівність 14 + 2x > 44 є математичною моделлю задачі про периметр паралелограма.
Якщо в цю нерівність замість змінної x підставити, наприклад, число 16, то отримаємо правильну числову нерівність 14 + 32 > 44. У такому разі говорять, що число 16 є розв’язком нерівності 14 + 2x > 44.
Означення. Розв’язком нерівності з однією змінною називають значення змінної, яке перетворює її в правильну числову нерівність.
![]() Так, кожне із чисел 15,1; 20; 10 3 є розв’язком нерівності
Так, кожне із чисел 15,1; 20; 10 3 є розв’язком нерівності
14 + 2x > 44, а число 10 не є її розв’язком.
Зауваження. Означення розв’язку нерівності аналогічне означенню кореня рівняння. Проте не прийнято говорити «корінь нерівності».
Означення.Розв’язати нерівність означає знайти всі її розв’язки або довести, що розв’язків не існує.
Усі розв’язки нерівності утворюють множину розв’язків нерівності. Якщо нерівність розв’язків не має, то говорять, що множиною її розв’язків є порожня множина. Нагадаємо, що порожню множину позначають символом ∅.
4. Нерівності з однією змінною
Таким чином, можна сказати, що розв’язати нерівність означає знайти множину її розв’язків.
Наприклад, у задачі «розв’яжіть нерівність x2 > 0» відповідь буде такою: «усі дійсні числа, крім числа 0».
Очевидно, що нерівність | x | < 0 розв’язків не має, тобто множиною її розв’язків є порожня множина.
Означення. Нерівності називають рівносильними, якщо вони мають одну й ту саму множину розв’язків.
Наведемо кілька прикладів.
![]() Нерівності x2 m 0 і x m0 є рівносильними. Справді, кожна з них має єдиний розв’язок x = 0.
Нерівності x2 m 0 і x m0 є рівносильними. Справді, кожна з них має єдиний розв’язок x = 0.
Нерівності x2 > –1 і | x | > –2 є рівносильними, оскільки мно жиною розв’язків кожної з них є множина дійсних чисел.
![]() Оскільки кожна з нерівностей x < −1 і 0x < –3 розв’язків не має, то вони також є рівносильними.
Оскільки кожна з нерівностей x < −1 і 0x < –3 розв’язків не має, то вони також є рівносильними.

![]() 4.1.° Які із чисел –4; –0,5; 0;
4.1.° Які із чисел –4; –0,5; 0; ![]() ; 2 є розв’язками нерівності: 1) x >
; 2 є розв’язками нерівності: 1) x > ![]() ; 3) 3x > x – 1; 5) x − 1 > 1;
; 3) 3x > x – 1; 5) x − 1 > 1;
2) xm5; 4) x2 − 9 m 0; 6) 1 > 1? x
4.2.° Яке з наведених чисел є розв’язком нерівності (x – 2)2 (x – 5) > > 0:
1) 3; 2) 2; 3) 6; 4) –1?
4.3.° Чи є розв’язком нерівності 6x + 1 m2 + 7x число:
1) –0,1; 2) –2; 3) 0; 4) –1; 5) 2?
4.4.° Назвіть будь-які два розв’язки нерівності x + 5 > 2x + 3.
¿ 4.5.° Чи є число 1,99 розв’язком нерівності x < 2? Чи існують розв’язки даної нерівності, більші за 1,99? У разі ствердної відповіді наведіть приклад такого розв’язку.
¿ 4.6.° Чи є число 4,001 розв’язком нерівності x > 4? Чи існують розв’язки даної нерівності, менші від 4,001? У разі ствердної відповіді наведіть приклад такого розв’язку.
4.7.° Множиною розв’язків якої з даних нерівностей є порожня множина:
1) (x – 3)2 > 0; 3) (x – 3)2 < 0;
2) (x − 3)2 l 0; 4) (x − 3)2 m 0?
4.8.° Які з наведених нерівностей не мають розв’язків:
1) 0x > –2; 2) 0x < 2; 3) 0x < –2; 4) 0x > 2?
4.9.° Множиною розв’язків якої з наведених нерівностей є множина дійсних чисел:
1) 0x > 1; 2) 0x > 0; 3) 0x > –1; 4) x + 1 > 0?
4.10.° Розв’язком якої з даних нерівностей є будь-яке дійсне число:
![]() 1) x2 > 0; 2) x > –x; 3) −x2 m 0; 4) xl 0?
1) x2 > 0; 2) x > –x; 3) −x2 m 0; 4) xl 0?
4.11.• Серед зазначених нерівностей укажіть нерівність, розв’язком якої є будь-яке дійсне число, і нерівність, що не має розв’язків:
2 2
![]()
![]() x + 1 x − 1 1) 2 l 0; 3) 2 l1; x x − 1 x2 + 1 x2
x + 1 x − 1 1) 2 l 0; 3) 2 l1; x x − 1 x2 + 1 x2
2) x2 + 1 < 1; 4) x2 + 1 l 0.
4.12.• Розв’яжіть нерівність:
1) ![]() 22 + 2 > 0; 7) xx+− 22 2 l 0; x
22 + 2 > 0; 7) xx+− 22 2 l 0; x
2) 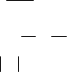 (x + 2)2 > 0; 8) x + 12 < 12 + 2;
(x + 2)2 > 0; 8) x + 12 < 12 + 2;
x x
3) (x + 2)2 m 0; 9) x l −x2; x+ 2 2 4) > 0; 10) | x | > –x ; x+ 2
x+ 2 2
5)  > ; 11) | x | > x; x+ 2 3
> ; 11) | x | > x; x+ 2 3
6) ![]() x+ 2 2 > 0; 12) x l −x.
x+ 2 2 > 0; 12) x l −x.
x− 2
¿ 4.13.• Знайдіть множину розв’язків нерівності:
1) | x | > 0; 4) x m− 1;
2) ![]() x m 0; 5) | x | > –3;
x m 0; 5) | x | > –3;
1
3) ![]() | x | < 0; 6) > −3.
| x | < 0; 6) > −3.
x
4. 14.• Чи рівносильні нерівності:
1 2
1) ![]() < 1 і x > 1; 3) (x + 5) < 0 і | x – 4 | < 0; x
< 1 і x > 1; 3) (x + 5) < 0 і | x – 4 | < 0; x
2)  x lx і xl1; 4) x m0 і x m 0?
x lx і xl1; 4) x m0 і x m 0?
ВПРаВи дЛЯ ПоВтоРеннЯ
4.15. Розв’яжіть рівняння:
1) 9 – 7 (x + 3) = 5 – 6x;
2) ![]() x+ 3 − x− 4 = 1;
x+ 3 − x− 4 = 1;
2 7
3) (x + 7)2 – (x – 2)2 = 15;
4) 5x – 2 = 3 (3x – 1) – 4x – 4; 5) 6x + (x – 2) (x + 2) = (x + 3)2 – 13; 6) (x + 6) (x – 1) – (x + 3) (x – 4) = 5x.
4.16. Велосипедист проїхав із села до озера й повернувся назад, витративши на весь шлях 1 год. Із села до озера він їхав зі швидкістю 15 км/год, а повертався зі швидкістю 10 км/год. Знайдіть відстань від села до озера.
 5. Розв’язування лінійних нерівностей з однією змінною. Числові проміжки
5. Розв’язування лінійних нерівностей з однією змінною. Числові проміжки
Властивості числових рівностей допомагали нам розв’язувати рівняння. Аналогічно властивості числових нерівностей допоможуть розв’язувати нерівності.
Розв’язуючи рівняння, ми заміняли його іншим, простішим рівнянням, рівносильним даному. За аналогічною схемою розв’язують і нерівності.
Під час заміни рівняння на йому рівносильне використовують теореми про перенесення доданків з однієї частини рівняння в другу та про множення обох частин рівняння на одне й те саме відмінне від нуля число.
Аналогічні правила застосовують і під час розв’язування нерівностей.
Якщо який-небудь доданок перенести з однієї частини нерівності в другу, змінивши при цьому його знак на протилежний, то отримаємо нерівність, рівносильну даній.
Якщо обидві частини нерівності помножити (поділити) на одне й те саме додатне число, то отримаємо нерівність, рівносильну даній.
Якщо обидві частини нерівності помножити (поділити) на одне й те саме від’ємне число, змінивши при цьому знак нерівності на протилежний, то отримаємо нерівність, рівносильну даній.
За допомогою цих правил розв’яжемо нерівність, отриману в задачі про периметр паралелограма (див. п. 4).
Маємо: 14 + 2x > 44.
Переносимо доданок 14 у праву частину нерівності:
2x > 44 –14.
Звідси 2x > 30.
Поділивши обидві частини нерівності на 2, отримуємо: x > 15.
Зауважимо, що отримана нерівність рівносильна заданій нерівності. Множина її розв’язків складається з усіх чисел, які більші за 15. Цю множину називають числовим проміжком і позначають так: (15; +∞) (читають: «проміжок від 15 до плюс нескінченності»).
У цій задачі відповідь можна записати одним зі способів: (15; +∞) або x > 15.
Точки координатної прямої, які зображають розв’язки нерівності x > 15, розміщені праворуч від точки, яка зображає число 15, і утворюють промінь, у якого «виколото» початок (рис. 5.1).
![]()
15 15 а б
Рис. 5.1
Зауважимо, що для зображення на рисунку числового проміжку використовують два способи: за допомогою або штриховки (рис. 5.1, а), або дужки (рис. 5.1, б). Ми використовуватимемо другий спосіб.
![]() Приклад 1 Розв’яжіть нерівність 3 +
Приклад 1 Розв’яжіть нерівність 3 + ![]() x m7 + x.
x m7 + x.
2
Розв’язання. Перенесемо доданок x з правої частини нерівності в ліву, а доданок 3 — з лівої частини в праву та зведемо подібні
члени:
−x + x m7 − 3;
2
![]() x
x
−m 4.
2
Помноживши обидві частини останньої нерівності на –2, отримаємо:
xl −8.
![]() Множиною розв’язків цієї нерівності є числовий проміжок, який позначають так:
Множиною розв’язків цієї нерівності є числовий проміжок, який позначають так:
[–8; +∞) (читають: «проміжок від –8 до плюс
–8 нескінченності, включаючи –8»).
Точки координатної прямої, які зобража- Рис. 5.2 ють розв’язки нерівності xl −8, утворюють промінь (рис. 5.2).
Відповідь можна записати одним зі способів: [–8; +∞) або xl −8. ◄
![]() Приклад 2 Розв’яжіть нерівність 2 (2 – 3x) > 3 (x + 6) – 5.
Приклад 2 Розв’яжіть нерівність 2 (2 – 3x) > 3 (x + 6) – 5.
Розв’язання. Запишемо ланцюжок нерівностей, рівносильних даній:
|
|
4 – 6x > 3x + 18 – 5; 4 – 6x > 3x + 13; –3x – 6x > –4 + 13; –9x > 9; x < –1. Множиною розв’язків останньої нерівності є числовий проміжок, який позначають так: |
|
–1 Рис. 5.3 |
(–∞; –1) (читають: «проміжок від мінус нескінченності до –1»). Точки координатної прямої, які зображають розв’язки нерівності x < –1, розміщені ліворуч від точки –1 (рис. 5.3) та |
утворюють промінь, у якого «виколото» початок.
Відповідь можна записати одним зі способів: (–∞; –1) або x < –1. ◄
![]()
![]() Приклад 3 Розв’яжіть нерівність x− 1 + x m 1.
Приклад 3 Розв’яжіть нерівність x− 1 + x m 1.
2 3 6
Розв’язання. Запишемо ланцюжок рівносильних нерівностей:
x− 1 x 1
![]() 6æ + 6æ m6æ ;
6æ + 6æ m6æ ;
2 3 6
3x − 3 + 2xm1; 5xm 4;
xm![]() .
.
Множиною розв’язків останньої нерівності є числовий промі жок, який позначають так: −×; ![]() 54 (читають: «проміжок від мінус не-
54 (читають: «проміжок від мінус не-
скінченності до ![]() , включаючи
, включаючи ![]() »). Точки
»). Точки ![]() координатної прямої, які зображають розв’язки
координатної прямої, які зображають розв’язки ![]() нерівності xm
нерівності xm![]() , утворюють промінь (рис. 5.4).
, утворюють промінь (рис. 5.4).
Рис. 5.4 Відповідь можна записати одним зі способів:
−×; ![]() 54 або xm
54 або xm ![]() 54. ◄
54. ◄
![]() Приклад 4 Розв’яжіть нерівність 3 2( x − 1) + 7 l 2 3( x + 1).
Приклад 4 Розв’яжіть нерівність 3 2( x − 1) + 7 l 2 3( x + 1).
Розв’язання. Маємо: 6x − 3 + 7 l 6x + 2; 6x − 6xl 2 − 4; 0xl −2.
Остання нерівність при будь-якому значенні x перетворюється в правильну числову нерівність 0 l −2. Отже, шукана множина розв’язків збігається з множиною дійсних чисел.
Відповідь: x — будь-яке число. ◄
Цю відповідь можна записати інакше: (–∞; +∞) (читають: «проміжок від мінус нескінченності до плюс нескінченності»). Цей числовий проміжок називають числовою прямою.
![]() Приклад 5 Розв’яжіть нерівність 4 (x – 2) – 1 < 2 (2x – 9). Розв’язання. Маємо:
Приклад 5 Розв’яжіть нерівність 4 (x – 2) – 1 < 2 (2x – 9). Розв’язання. Маємо:
4x – 8 – 1 < 4x – 18; 4x – 4x < 9 – 18; 0x < –9.
Отримана нерівність при будь-якому значенні x перетворюється в неправильну числову нерівність 0 < –9.
У цій задачі відповідь можна записати одним зі способів: розв’язків немає або ∅. ◄
Кожна з нерівностей, які було розглянуто в прикладах 1–5, зводилася до рівносильної нерівності одного із чотирьох видів: ax > b, ax < b, ax bl , ax bm , де x — змінна, a і b — деякі числа. Такі нерівності називають лінійними нерівностями з однією
змінною.
Наведемо таблицю позначень і зображень вивчених числових проміжків:
|
Нерівність |
Проміжок |
Зображення |
|
x > a |
(a; +∞) |
|
|
x < a |
(–∞; a) |
|
|
x al |
[a; +∞) |
|
|
x am |
(–∞; a] |
|
1. сформулюйте правила, за допомогою яких можна отримати нерівність, рівносильну даній.
2. Які нерівності називають лінійними нерівностями з однією змінною?
3. Як записують, читають і зображають проміжок, який є множиною розв’язків нерівності виду x > a? x < a? x al ? x am ?
4.  розв’язком нерівності є будь-яке число. Як у такому випадку записують, читають і називають проміжок, який є множиною розв’язків нерівності?
розв’язком нерівності є будь-яке число. Як у такому випадку записують, читають і називають проміжок, який є множиною розв’язків нерівності?
ВПРаВи
¿ 5.1.° Зобразіть на координатній прямій проміжок:
1) [–5; +∞); 2) (–5; +∞); 3) (–∞; –5); 4) (–∞; –5].
¿ 5.2.° Зобразіть на координатній прямій і запишіть проміжок, який задається нерівністю:
1) x < 8; 2) xm−4; 3) xl −1; 4) x > 0.
¿ 5.3.° Зобразіть на координатній прямій і запишіть проміжок, який задається нерівністю:
1) xm 0; 2) xl![]() ; 3) x > –1,4; 4) x < 16.
; 3) x > –1,4; 4) x < 16.
5.4.° Укажіть найменше ціле число, яке належить проміжку:
1) (6; +∞); 2) [6; +∞); 3) (–3,4; +∞); 4) [–0,9; +∞).
5.5.° Укажіть найбільше ціле число, яке належить проміжку:
1) (–∞; –4); 2) (–∞; –6,2]; 3) (–∞; 1]; 4) (–∞; –1,8).
5.6.° Яким з наведених проміжків належить число –7:
1) (–∞; –7); 2) [–7; +∞); 3) (–∞; 0]; 4) (–∞; –6)?
5.7.° Якому з наведених проміжків не належить число 9:
1) (8,99; +∞); 2) (–∞; 10); 3) (–∞; 8,99]; 4) [9; +∞)?
5.8.° Розв’яжіть нерівність:
1) 6x > 18; 6) –10x < 0; 11) 4 – x < 5;
2) −2xl10; 7) 2![]() xm−1
xm−1![]() ; 12) 5 − 8xl 6;
; 12) 5 − 8xl 6;
3) ![]() x < 9; 8) −7x >
x < 9; 8) −7x > ![]() ; 13) 12 + 4xl 6x;
; 13) 12 + 4xl 6x;
4) ![]() 0,1xl 0; 9) 7x – 2 > 19; 14) 36 – 2x < 4x; x+ 2
0,1xl 0; 9) 7x – 2 > 19; 14) 36 – 2x < 4x; x+ 2
5) x > 24; 10) 5x + 16 m6; 15) ![]() < 2.
< 2.
5
5.9.° Розв’яжіть нерівність:
1) 5x < 30; 5) −3x < ![]() ; 9) 13 − 6xl −23;
; 9) 13 − 6xl −23;
2) −4xm−16; 6) −2![]() x > 1
x > 1![]() ; 10) 5 – 9x > 16;
; 10) 5 – 9x > 16;
3) ![]() xm6; 7) 4x + 5 > –7; 11) 3x + 2 m− 7x;
xm6; 7) 4x + 5 > –7; 11) 3x + 2 m− 7x;
x− 3
4) −12xl 0; 8) 9 − xl 2x; 12) ![]() > −1.
> −1.
4
5.10.° Розв’яжіть нерівність:
1) 0x > 10; 3) 0x > –8; 5) 0xl1; 7) 0xm 0; 2) 0x < 15; 4) 0x < –3; 6) 0xm2; 8) 0x > 0.
5.11.° Знайдіть найменший цілий розв’язок нерівності:
1) 5xl 40; 2) 5x > 40; 3) –2x < –3; 4) –7x < 15.
5.12.° Знайдіть найбільший цілий розв’язок нерівності:
1) 8xm−16; 2) 8x < –16; 3) 3x < 10; 4) –6x > –25.
5.13.° При яких значеннях a вираз 6a + 1 набуває від’ємних значень?
5.14.° При яких значеннях b вираз 7 – 2b набуває додатних значень?
5.15.° При яких значеннях m значення виразу 2 – 4m не менші від –22?
5.16.° При яких значеннях n значення виразу 12n – 5 не більші за –53?
5.17.° При яких значеннях x має зміст вираз:
![]() 1) 4x + 20; 2) 5 − 14x; 3) ?
1) 4x + 20; 2) 5 − 14x; 3) ?
5.18.° Знайдіть область визначення функції:

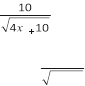 1) f x( ) = 13 − 2x; 2) f x( ) = x .
1) f x( ) = 13 − 2x; 2) f x( ) = x .
− −x 1
|
5.19.° Розв’яжіть нерівність: |
|
|
1) 8x + 2 < 9x – 3; |
4) 3 − 11yl −3y + 6; |
|
2) 6 – 6x > 10 – 4x; |
5) –8p – 2 < 3 – 10p; |
|
3) 6y + 8 m10y − 8; 5.20.° Розв’яжіть нерівність: |
6) 3m − 1 m1,5m + 5. |
|
1) 4 + 11x > 7 + 12x; |
3) 3x – 10 < 6x + 2; |
|
2) 35x − 28 m32x + 2; |
4) 6x − 3 l 2x − 25. |
5.21.° При яких значеннях c значення двочлена 9c – 2 не більші за відповідні значення двочлена 4c + 4?
5.22.° При яких значеннях k значення двочлена 11k – 3 не менші від відповідних значень двочлена 15k – 13?
5.23.° Розв’яжіть нерівність:
1) 4x + x < 11; 3) 5x − x > −4;
3 2 7
![]()
![]() 2x 3x 1 x 1
2x 3x 1 x 1
|
− 3 4 6 5.24.° Розв’яжіть нерівність: |
− 8 4 |
|
6 4 |
10 5 |
2) l ; 4) mx.
5.25.• Розв’яжіть нерівність:
1) 3 − 5 2( x + 4) l7 − 2x; 2) 6x − 3 (x − 1) m2 + 5x;
3) x − 2 (x − 1) l10 + 3 (x + 4);
4) 2 (2x – 3,5) – 3 (2 – 3x) < 6 (1 – x); 5) (x + 1) (x − 2) m (x − 3) (x + 3);
6) (4x − 3)2 + (3x + 2)2 l (5x + 1)2;
2x − 1 3x − 5
7) l ;
4 5
8) ![]() 3x+ 7 − 5x− 2 < x;
3x+ 7 − 5x− 2 < x;
4 2
9) (x − 5) (x + 1) m3 + (x − 2)2;
10) ![]() x+ 1 − x− 3 > 2 + x;
x+ 1 − x− 3 > 2 + x;
2 3 6
11) (6x − 1)2 − 4x x(9 − 3) m1;
12) ![]() x− 3 − x+ 4 > x− 8.
x− 3 − x+ 4 > x− 8.
9 4 6
5.26.• Знайдіть множину розв’язків нерівності:
1) 3 (4x + 9) + 5 > 7 (8 – x); 2) (2 − y) (3 + y) m (4 + y) (6 − y);
3) (y + 3) (y – 5) – (y – 1)2 > –16; x 2x − 6
4) − 1l ;
3
5)  2x − x− 1 − x+ 2 < 0;
2x − x− 1 − x+ 2 < 0;
3 6 2
6) y− 1 − 2y+ 1 − y < 2.
2 8
5.27.• Знайдіть найбільший цілий розв’язок нерівності:
1) 7 (x + 2) – 3 (x – 8) < 10;
2) (x – 4) (x + 4) – 5x > (x – 1)2 – 17.
5.28.• Знайдіть найменший цілий розв’язок нерівності:
1) ![]() 4x+ 13 − 5 + 2x > 6 − 7x − 2;
4x+ 13 − 5 + 2x > 6 − 7x − 2;
10 4 20
2) (x − 1) (x + 1) − (x − 4) (x + 2) l 0.
![]() 5.29.• Скільки цілих від’ємних розв’язків має нерівність x − x+ 7 − 11x+ 30 < x− 5?
5.29.• Скільки цілих від’ємних розв’язків має нерівність x − x+ 7 − 11x+ 30 < x− 5?
4 12 3
5.30.• Скільки натуральних розв’язків має нерівність
![]() 2 − 3xl 1 − 5x+ 6 ?
2 − 3xl 1 − 5x+ 6 ?
4 5 8
5.31.• При яких значеннях x є правильною рівність:
1) | x – 5 | = x – 5; 2) | 2x + 14 | = –2x – 14?
5.32.• При яких значеннях y є правильною рівність:
![]()
![]() 1) y+ 7 = 1; 2) 6 −y = 1? y+ 7 y− 6
1) y+ 7 = 1; 2) 6 −y = 1? y+ 7 y− 6
5.33.• При яких значеннях a рівняння:
1) x2 + 3x – a = 0 не має коренів;
2) 2x2 – 8x + 5a = 0 має хоча б один корінь?
5.34.• При яких значеннях b рівняння:
1) 3x2 – 6x + b = 0 має два різних корені; 2) x2 – x – 2b = 0 не має коренів?
5.35.• Човен проплив деяку відстань за течією річки, а потім повернувся назад, витративши на всю подорож не більше п’яти годин. Швидкість човна в стоячій воді дорівнює 5 км/год, а швидкість течії — 1 км/год. Яку найбільшу відстань міг пропливти човен за течією річки?
5.36.• Беруть чотири послідовних цілих числа та розглядають різницю добутків крайніх і середніх чисел. Чи існують такі чотири послідовних цілих числа, для яких ця різниця більша за нуль?
5.37.• У коробці лежать сині та жовті кулі. Кількість синіх куль відноситься до кількості жовтих як 3 : 4. Яка найбільша кількість синіх куль може бути в коробці, якщо всього куль не більше за 44?
5.38.• У саду ростуть яблуні, вишні та сливи, кількості яких відносяться як 5 : 4 : 2 відповідно. Якою може бути найменша кількість вишень, якщо всього дерев у саду не менше від 120?
5.39.• Сторони трикутника дорівнюють 8 см, 14 см і a см, де a — натуральне число. Якого найбільшого значення може набувати a?
5.40.• Сума трьох послідовних натуральних парних чисел не менша від 85. Знайдіть найменші три числа, які задовольняють цю умову.
5.41.• Сума трьох послідовних натуральних чисел, які кратні 5, не більша за 100. Які найбільші три числа задовольняють цю умову?
5.42.• При яких значеннях x визначена функція:
1)  f x( ) = x + 4 + 1 ; 3) f x( ) = 1 − 8 ; x− 2 3x+ 9 x − 2
f x( ) = x + 4 + 1 ; 3) f x( ) = 1 − 8 ; x− 2 3x+ 9 x − 2
2) ![]() f x( ) = 24 − 8x + 2 6− 16; 4) f x( ) = x + 1 + x24− 1? x
f x( ) = 24 − 8x + 2 6− 16; 4) f x( ) = x + 1 + x24− 1? x
5.43.• При яких значеннях змінної має зміст вираз:
|
5.44.•• Розв’яжіть рівняння: |
6
3x− 21 x |
|
1) | x – 3 | + x = 15; |
3) | 3x – 12 | – 2x = 1; |
|
2) | x + 1 | – 4x = 14; 5.45.•• Розв’яжіть рівняння: |
4) | x + 2 | – x = 1. |
|
1) | x + 5 | + 2x = 7; |
2) | 3 – 2x | – x = 9. |
5.46.•• Побудуйте графік функції:
1) y = | x – 2 |; 3) y = | x – 1 | + x.
2) y = | x + 3 | – 1;
5.47.•• Побудуйте графік функції:
1) y = | x + 4 |; 3) y = | 2x – 6 | – x.
2) y = | x – 5 | + 2;
5.48.•• При яких значеннях a рівняння: 1) 4x + a = 2 має додатний корінь;
2) (a + 6) x = 3 має від’ємний корінь;
3) (a – 1) x = a2 – 1 має єдиний додатний корінь?
5. 49.•• При яких значеннях m рівняння:
1) 2 + 4x = m – 6 має невід’ємний корінь; 2) mx = m2 – 7m має єдиний від’ємний корінь?
5.50.* Знайдіть усі значення a, при яких має два різних корені рівняння:
1) ax2 + 2x – 1 = 0;
2) (a + 1) x2 – (2a – 3) x + a = 0; 3) (a – 3) x2 – 2 (a – 5) x + a – 2 = 0.
5.51.* Знайдіть усі значення a, при яких не має коренів рівняння (a – 2) x2 + (2a + 1) x + a = 0.
5.52.* Чи існує таке значення a, при якому не має розв’язків нерівність (у разі ствердної відповіді вкажіть це значення):
1) ax > 3x + 4; 2) (a2 − a − 2) x am − 2?
5.53.* Чи існує таке значення a, при якому будь-яке число є розв’язком нерівності (у разі ствердної відповіді вкажіть це значення):
1) ax > –1 – 7x; 2) (a2 − 16) x am + 4?
5.54.* Для кожного значення a розв’яжіть нерівність:
1) ax > 0; 3) ax al ; 5) (a – 2) x > a2 – 4; 2) ax < 1; 4) 2 (x – a) < ax – 4; 6) (a + 3) x am 2 − 9.
5.55.* Для кожного значення a розв’яжіть нерівність:
1) a x2 m 0; 2) a + x < 2 – ax; 3) (a + 4) x > 1.
![]() ВПРаВи дЛЯ ПоВтоРеннЯ
ВПРаВи дЛЯ ПоВтоРеннЯ
|
5.56. Розв’яжіть рівняння: |
|
|
1) 6x – 5x2 = 0; |
4) 3x2 + 8x – 3 = 0; |
|
2) 25x2 = 81; |
5) x2 + x – 12 = 0; |
|
3) 4x2 – 7x – 2 = 0; |
6) 2x2 + 6x + 7 = 0. |
5.57. Відомо, що m і n — послідовні цілі числа. Яке з поданих тверджень завжди є правильним: 1) добуток mn більший за m;
2) добуток mn більший за n; 3) добуток mn є парним числом; 4) добуток mn є непарним числом?
5.58. Порівняйте значення виразів:
1)  3 98 і 4 72; 3)
3 98 і 4 72; 3) ![]()
![]() .
.
2) ![]() 68 і 45;
68 і 45;
5.59. Щоб наповнити басейн водою через одну трубу, потрібно в 1,5 раза більше часу, ніж для того, щоб наповнити його через другу трубу. Якщо ж відкрити одночасно обидві труби, то басейн наповниться за 6 год. За скільки годин можна наповнити басейн через кожну трубу окремо?
 УЧиМоСЯ Робити неСтандаРтні кРоки
УЧиМоСЯ Робити неСтандаРтні кРоки
5.60. Трицифрове число n є таким, що числа n – 6, n – 7 і n – 8 кратні числам 7, 8 і 9 відповідно. Знайдіть число n.
 6. Системи лінійних нерівностей з однією змінною
6. Системи лінійних нерівностей з однією змінною
![]() Розглянемо вираз 2x − 1 + 5 − x. Знайдемо множину допустимих значень змінної x, тобто всі значення змінної x, при яких даний вираз має зміст. Цю множину називають областю визначення виразу.
Розглянемо вираз 2x − 1 + 5 − x. Знайдемо множину допустимих значень змінної x, тобто всі значення змінної x, при яких даний вираз має зміст. Цю множину називають областю визначення виразу.
Оскільки підкореневий вираз може набувати тільки невід’ємних значень, то мають одночасно виконуватися дві нерівності: 2x − 1l 0 і 5 − xl 0. Тобто шукані значення змінної x — це всі спільні розв’язки зазначених нерівностей.
![]() Якщо треба знайти всі спільні розв’язки двох або кількох нерівностей, то говорять, що треба розв’язати систему нерівностей. Як і систему рівнянь, систему нерівностей записують за допомогою фігурної дужки. Так, для знаходження області визначення виразу 2x − 1 + 5 − x треба розв’язати систему нерівностей
Якщо треба знайти всі спільні розв’язки двох або кількох нерівностей, то говорять, що треба розв’язати систему нерівностей. Як і систему рівнянь, систему нерівностей записують за допомогою фігурної дужки. Так, для знаходження області визначення виразу 2x − 1 + 5 − x треба розв’язати систему нерівностей
2x − 1l 0,
5 − xl 0. (*)
Означення. Розв’язком системи нерівностей з однією змінною називають значення змінної, яке перетворює кожну нерівність системи в правильну числову нерівність.
Наприклад, числа 2, 3, 4, 5 є розв’язками системи (*), а число 7 не є її розв’язком.
Означення. Розв’язати систему нерівностей означає знайти всі її розв’язки або довести, що розв’язків немає.
Усі розв’язки системи нерівностей утворюють множину розв’язків системи нерівностей. Якщо система розв’язків не має, то говорять, що множиною її розв’язків є порожня множина.
Таким чином, можна сказати, що розв’язати систему нерівностей означає знайти множину її розв’язків.
![]() 0xl − 1, Наприклад, у задачі «Розв’яжіть систему нерівностей » x l 0
0xl − 1, Наприклад, у задачі «Розв’яжіть систему нерівностей » x l 0
відповідь буде такою: «множина дійсних чисел».
xm5,
Очевидно, що множина розв’язків системи нерівностей xl 5
складається з єдиного числа 5.
x > 5,
Система нерівностей x < 5 розв’язків не має, тобто множиною
її розв’язків є порожня множина.
Розв’яжемо систему (*). Перетворюючи кожну нерівність сис-
2xl1, xl ![]() 1,
1,
теми в рівносильну їй, отримуємо: −xl −5; xm52.
Множина розв’язків останньої системи складається з усіх чисел, які не менші від ![]() і не більші за 5, тобто з усіх чисел, які задовольняють нерівність
і не більші за 5, тобто з усіх чисел, які задовольняють нерівність ![]() m mx 5. Ця множина є числовим проміжком,
m mx 5. Ця множина є числовим проміжком,
1 1
який позначають так: ![]() 2; 5 (читають: «проміжок від
2; 5 (читають: «проміжок від ![]() 2 до 5,
2 до 5,
включаючи ![]() і 5»).
і 5»).
Відповідь до задачі про знаходження області визначення виразу
![]() 2x − 1 + 5 − x можна записати одним зі способів:
2x − 1 + 5 − x можна записати одним зі способів: ![]() 12; 5 або
12; 5 або ![]() m mx 5.
m mx 5.
Точки, які зображають розв’язки системи (*), розміщені між 1
точками A ![]() і B (5), включаючи точки A і B (рис. 6.1). Вони 2
і B (5), включаючи точки A і B (рис. 6.1). Вони 2
утворюють відрізок.
![]()
![]() 5
5 ![]() 5
5
Рис. 6.1 Рис. 6.2
![]() 1 +× і (–∞; 5]
1 +× і (–∞; 5]
Зауважимо, що всі спільні точки проміжків 2;
1
утворюють проміжок ![]() 2; 5 (рис. 6.2). Говорять, що проміжок 12; 5 є перерізом проміжків
2; 5 (рис. 6.2). Говорять, що проміжок 12; 5 є перерізом проміжків ![]() 12; +× і (–∞; 5]. Записують:
12; +× і (–∞; 5]. Записують:
![]() 1; +∞(−×; 5] =
1; +∞(−×; 5] = ![]() 12; 5.
12; 5.
2
![]()
![]() Проміжки 12; +× і (–∞; 5] є множинами розв’язків відповідно
Проміжки 12; +× і (–∞; 5] є множинами розв’язків відповідно
нерівностей xl і xm5. Тоді можна сказати, що множина
![]() xl 1,
xl 1,
розв’язків системи 2 є перерізом множин розв’язків кожної
xm5
з нерівностей, які складають систему.
Отже, щоб розв’язати систему нерівностей, треба знайти переріз множин розв’язків нерівностей, які складають систему.
3x − 1 > −7,
![]() Приклад 1 Розв’яжіть систему нерівностей 3 − 4x > −9.
Приклад 1 Розв’яжіть систему нерівностей 3 − 4x > −9.
3x > −6, x > −2,
Розв’язання. Маємо:
|
|
За допомогою координатної прямої знайдемо переріз множин розв’язків нерівностей |
|
–2 3 Рис. 6.3 |
даної системи, тобто переріз проміжків (–∞; 3) і (–2; +∞) (рис. 6.3). Шуканий переріз складається із чисел, які задовольняють нерівність –2 < x < 3. Ця множина є числовим проміж- |
−4x > −12; x < 3.
ком, який позначають (–2; 3) (читають: «проміжок від –2 до 3»).
Відповідь можна записати одним зі способів: (–2; 3) або –2 < x < 3. ◄
4x − 3 < 1,
![]() Приклад 2 Розв’яжіть систему нерівностей
Приклад 2 Розв’яжіть систему нерівностей
|
4x < 4, x < 1, Розв’язання. Маємо: −xm2; xl −2. За допомогою координатної прямої знайдемо переріз проміжків (–∞; 1) і [–2; +∞), |
|
|
які є множинами розв’язків нерівностей даної системи (рис. 6.4). Шуканий переріз складається із чисел, які задовольняють нерівність –2 m x < 1. Ця множина є числовим проміжком, який позначають [–2; 1) (читають: «проміжок від –2 до 1, включаючи –2»). |
–2 1 Рис. 6.4 |
3 − xm5.
Відповідь можна записати одним зі способів: [–2; 1) або –2 m x < 1. ◄
![]() xm1, Приклад 3 Розв’яжіть систему нерівностей x > −2.
xm1, Приклад 3 Розв’яжіть систему нерівностей x > −2.
Множиною розв’язків даної системи є переріз проміжків (–∞; 1] і (–2; +∞) (рис. 6.5). Цей переріз є числовим проміжком, який позначають (–2; 1] (читають: «проміжок від –2 до 1, включаючи 1»). Відповідь: (–2; 1]. ◄
![]()
|
–2 1 |
–5 1 |
|
Рис. 6.5 |
Рис. 6.6 |
![]() Приклад 4 Знайдіть область визначення функції
Приклад 4 Знайдіть область визначення функції
![]() y = 1 + x + 5. x− 1
y = 1 + x + 5. x− 1
Розв’язання. Шукана область визначення — це множина
x − 1 > 0, x > 1,
розв’язків системи нерівностей x + 5 l 0. Маємо: xl −5.
Зобразимо на координатній прямій переріз проміжків (1; +∞) і [–5; +∞) (рис. 6.6). Цим перерізом є проміжок (1; +∞). Відповідь: (1; +∞). ◄
Наведемо таблицю позначень і зображень числових проміжків, вивчених у цьому пункті:
|
Нерівність |
Проміжок |
Зображення |
|
a x bm m |
[a; b] |
|
|
a < x < b |
(a; b) |
|
|
a x b< m |
(a; b] |
|
|
a x bm < |
[a; b) |
|
1. Що називають областю визначення виразу?
2. У яких випадках говорять, що треба розв’язати систему нерівностей?
3. За допомогою якого символу записують систему нерівностей?
4. Що називають розв’язком системи нерівностей з однією змінною?
5. Що означає розв’язати систему нерівностей?
6.  Як записують, читають і зображають проміжок, який є множиною розв’язків нерівності виду a x bm m ? a < x < b? a x b< m ? a x bm < ?
Як записують, читають і зображають проміжок, який є множиною розв’язків нерівності виду a x bm m ? a < x < b? a x b< m ? a x bm < ?
ВПРаВи
6.1.° Які із чисел –6; –5; 0; 2; 4 є розв’язками системи нерівностей:
x − 2 < 0,
−2xm10?
6.2.° Розв’язком якої із систем нерівностей є число –3:
xl −3, x < −4, x > −4, x + 1 > −1,
1) xl 6; 2) x < 8; 3) x < 8; 4) x − 2 < 0?
¿ 6.3.° Зобразіть на координатній прямій проміжок:
1) (–3; 4); 2) [–3; 4]; 3) [–3; 4); 4) (–3; 4].
¿ 6.4.° Зобразіть на координатній прямій і запишіть проміжок, який задано нерівністю:
1) 0 < x < 5; 3) 0,2 mx < 102;
2) ![]() < xm2
< xm2![]() ; 4) −2 4, m mx −1.
; 4) −2 4, m mx −1.
6.5.° Запишіть усі цілі числа, які належать проміжку:
1) [3; 7]; 2) (2,9; 6]; 3) [–5,2; 1); 4) (–2; 2).
6.6.° Укажіть найменше і найбільше цілі числа, які належать проміжку:
1) [–12; –6]; 3) (–10,8; 1,6]; 2) (5; 11]; 4) [–7,8; –2,9].
6.7.° Зобразіть на координатній прямій і запишіть переріз проміжків:
|
1) [–1; 7] і [4; 9]; |
4) (–∞; 2,6) і (2,8; +∞); |
|
2) [3; 6] і (3; 8); |
5) [9; +∞) і [11,5; +∞); |
|
3) (–∞; 3,4) і (2,5; +∞); |
6) (–∞; –4,2] і (–∞; –1,3). |
6.8.° Укажіть на рисунку 6.7 зображення множини розв’язків сис-
x > −1,
теми нерівностей
xm6.
![]()
–1 6 –1 6 а в
![]()
–1 6 –1 6 б г
Рис. 6.7
6.9.° Укажіть на рисунку 6.8 зображення множини розв’язків подвійної нерівності −4 m mx 2.
![]()
–4 2 –4 2 а в
![]()
–4 2 –4 2 б г
Рис. 6.8
6.10.° Який із наведених проміжків є множиною розв’язків систе-
x > −1,
ми нерівностей x > 2:
1) (–∞; –1); 2) (–1; 2); 3) (2; +∞); 4) (–1; +∞)?
6.11.° Відомо, що a < b < c < d. Який із даних проміжків є перерізом проміжків (a; c) і (b; d):
1) (a; d); 2) (b; c); 3) (c; d); 4) (a; b)?
6.12.° Відомо, що m < n < k < p. Який із даних проміжків є перерізом проміжків (m; p) і (n; k):
1) (m; n); 2) (k; p); 3) (n; k); 4) (m; p)?
6.13.° Зобразіть на координатній прямій і запишіть множину розв’язків системи нерівностей:
|
xm2, 1) −1; xm |
x < 2, 3) −1; xl |
x > 2, 5) −1; xl |
xl 2, 7) m2; x |
|
xm2, 2) > −1; x |
xm2, 4) < −1; x |
x > 2, 6) −1; xm |
xl 2, 8) < 2. x |
6.14.° Розв’яжіть систему нерівностей:
x − 4 < 0, x − 2 < 1 + 3x,
1) 2xl −6; 6) 5x − 7 mx + 9;
x − 2 > 3, 3x − 6 mx − 1,
2) −3x < −12; 7) 11x + 13 < x + 3;
x + 6 > 2, 5x + 14 l18 − x,
3) ![]() x4 < 2; 8) 1 5, x + 1 < 3x − 2;
x4 < 2; 8) 1 5, x + 1 < 3x − 2;
6x + 3 l 0, 4x + 19 m5x − 1,
4) 7 − 4x < 7; 9) 10x < 3x + 21.
10x − 1l 3,
5) 7 − 3xl 2x − 3;
6.15.° Розв’яжіть систему нерівностей:
−4xm−12, 2 − 3x < 4x − 12,
|
x + 2 > 6; |
7 + 3xl 2x + 10; |
|
8 − xl 5, 2) − 7 m2; x |
x + 3 l 8, 5) x+ 1 |
1) 4)
3x − 3 < 5x, 5x − 2 l 2x + 1,
3) 7x − 10 < 5x; 6) 2x + 3 m33 − 3x.
6.16.° Знайдіть множину розв’язків нерівності:
|
1) –3 < x – 4 < 7; |
3) 0 8, m6 − 2x < 1 4, ; |
|
2) −2 4, m3x + 0 6, m3; 6.17.° Розв’яжіть нерівність: |
4) 4 < 5 |
|
1) 2 < x + 10 m14; |
3) −1 8, m1 − 7xm36; |
|
2) 10 < 4x – 2 < 18; |
x+ 1 4) 1 m |
4
−2xl −15,
6.18.° Скільки цілих розв’язків має система нерівностей 3x > −10?
6.19.° Знайдіть суму цілих розв’язків системи нерівностей
x + 8 l 4,
5x + 1 m 9.
6.20.° Скільки цілих розв’язків має нерівність −3 m7x − 5 < 16?
6.21.° Знайдіть найменший цілий розв’язок системи нерівностей
x + 8 l17,
x ![]() 2 > 4 5, .
2 > 4 5, .
6.22.° Знайдіть найбільший цілий розв’язок системи нерівностей
2x + 1 < −4, 3x − 6 m−12.
6.23.• Розв’яжіть систему нерівностей:
8 (2 − x) − 2x > 3,
1) −3 6( x − 1) − x < 2x;
![]() x+ 1 − 2x+ 3 > 1,
x+ 1 − 2x+ 3 > 1,
2) 4 3
6 (2x − 1) < 5 (x − 4) − 7;
2 (x − 3) m3x + 4 (x + 1),
3) 2
(x − 3) (x + 3) m (x − 4) − 1;
2 (x + 11) l 3 6( − x),
4) (x − 3) (x + 6) l (x + 5) (x − 4);
![]() 2x − x+ 1 mx+ 1,
2x − x+ 1 mx+ 1,
5) 2 3
(x + 5) (x − 3) + 41l (x − 6)2;
5x + 4 m2x − 8,
6) (x + 2) (x − 1) l (x + 3) (x − 2);
![]() x+ 2 < x+ 1,
x+ 2 < x+ 1,
7) 7 4
(x − 6) (x + 2) + 4x < (x − 7) (x + 7);
![]() 6x+ 1 − 5x− 1 > −1,
6x+ 1 − 5x− 1 > −1,
8) 6 5
2 (x + 8) − 3 (x + 2) < 5 − x.
6.24.• Знайдіть множину розв’язків системи нерівностей:
![]() 2x− 3 − 4x− 9 > 1,
2x− 3 − 4x− 9 > 1,
1) 5 6
5 (x − 1) + 7 (x + 2) > 3;
![]() x+ 1 − x+ 2 < x+ 12,
x+ 1 − x+ 2 < x+ 12,
2) 2 3 6
0 3, x − 19 m1 7, x − 5;
(x − 6)2 < (x − 2)2 − 8,
3)
3 2( x − 1) − 8 < 34 − 3 5( x − 9);
![]() 3x− 2 − 4x+ 1 m1,
3x− 2 − 4x+ 1 m1,
4) 3 4
(x − 1) (x − 2) > (x + 4) (x − 7). 6.25.• Знайдіть цілі розв’язки системи нерівностей:
x
2x − 1 < 1 7, − x, 3 − x4 < 1,
![]() 1) 3x − 2 lx − 8; 2) 2x − xl10.
1) 3x − 2 lx − 8; 2) 2x − xl10.
2
6.26.• Скільки цілих розв’язків має система нерівностей:
4x + 3 l 6x − 7, x − x 3+ 1 − x 6− 2 < 2,
![]() 1) 3 (x + 8) l 4 (8 − x); 2) 2x− 5 l − 3?
1) 3 (x + 8) l 4 (8 − x); 2) 2x− 5 l − 3?
3
6.27.• Знайдіть область визначення виразу:
1) 6x − 9 + 2x − 5; 3) 2x − 4 + 1 − x;
2) ![]() 3x + 5 − 1 ; 4) 12 − 3x − 5 .
3x + 5 − 1 ; 4) 12 − 3x − 5 .
15 − 5x x − 4
6.28.• При яких значеннях змінної має зміст вираз:
![]()
![]() 1) 8 − +x 1 ; 2) 7x − 35 + 2 1 ?
1) 8 − +x 1 ; 2) 7x − 35 + 2 1 ?
2 x x − 5x
6.29.• Розв’яжіть нерівність:
![]() 1) −3 < < 4; 2) −4 m1 −
1) −3 < < 4; 2) −4 m1 − ![]() x − 2 m−3.
x − 2 m−3.
3
6.30.• Розв’яжіть нерівність:
![]() 1) −2 m < 4; 2) 1 2, < 7
1) −2 m < 4; 2) 1 2, < 7![]() − 3x m1 4, .
− 3x m1 4, .
5
6.31.• Розв’яжіть систему нерівностей:
x < 4, 0 4, − 8xl 3 6, ,
1) x > 2, 3) 1 5, x − 2 < 4, x < 3 6, ; 4 1, x + 10 < 1 6, x + 5.
2x − 6 < 8,
2) 4 − 4x < 10,
8x − 9 > 3;
6.32.• Розв’яжіть систему нерівностей:
−x < 2, 3x − 1 < 2x + 2,
1) 2x > 7, 2) 2x + 1 > 8 − 5x,
x < −4; 5x − 25 m 0.
¿ 6.33.• Одна сторона трикутника дорівнює 4 см, а сума двох інших — 8 см. Знайдіть невідомі сторони трикутника, якщо довжина кожної з них дорівнює цілому числу сантиметрів.
6. 34.•• Розв’яжіть нерівність:
1) (x − 3) (x + 4) m 0; 4) 3x+ 6 < 0; x− 9
2x− 1
2) ![]() (x + 1) (2x – 7) > 0; 5) m 0; x+ 2 x− 8 5x+ 4
(x + 1) (2x – 7) > 0; 5) m 0; x+ 2 x− 8 5x+ 4
3) > 0; 6) l 0.
|
|
|
|
x− 1 6.35.•• Розв’яжіть нерівність: |
x− 6 |
|
1) (14 – 7x) (x 3) > 0; |
5x− 6 3) l 0; |
+
x+ 9
![]() 2) x− 8 > 0; 4) 4x+ 1 m 0.
2) x− 8 > 0; 4) 4x+ 1 m 0.
|
|
|
|
3x− 12 6.36.•• Розв’яжіть нерівність: |
x− 10 |
1) ![]() x − 2 m3 6, ; 4) 7 − 3x l1;
x − 2 m3 6, ; 4) 7 − 3x l1;
2) ![]() | 2x + 3 | < 5; 5) x + 3 + 2xl 6;
| 2x + 3 | < 5; 5) x + 3 + 2xl 6;
|
3) | x + 3 | > 9; 637.•• Розв’яжіть нерівність: |
6) | x – 4 | – 6x < 15. |
1) x − 6 l 2 4, ; 3) | x + 5 | – 3x > 4;
2) ![]()
![]() 5x + 8 m2; 4) x − 1 + xm3.
5x + 8 m2; 4) x − 1 + xm3.
6.38.* При яких значеннях a має хоча б один розв’язок система нерівностей:
xl 3, xm3,
1) x a< ; 2) x al ?
6.39.* ![]() a не має розв’язків система нерівностей:
a не має розв’язків система нерівностей:
x > 4, xm1,
1) x a< ; 2) x al ?
6.40.* При яких значеннях a множиною розв’язків системи нерів-
x > −1, ностей є проміжок:
x al
1) (–1; +∞); 2) [1; +∞)?
6.41.* Для кожного значення a розв’яжіть систему нерівностей
x < 2,
x am .
6.42.* Для кожного значення a розв’яжіть систему нерівностей
x < −3, x a> .
6.43.* При яких значеннях a множина розв’язків системи нерівно-
xl7, стей x a< містить рівно чотири цілих числа?
6.44.* При яких значеннях b множина розв’язків системи нерівно-
x < 5, стей містить рівно три цілих числа?
x bl
6.45.* При яких значеннях a найменшим цілим розв’язком системи
xl 6,
нерівностей x a> є число 9?
6.46.* При яких значеннях b найбільшим цілим розв’язком систе-
x bm ,
ми нерівностей x < −2 є число –6?
6.47.* При яких значеннях a корені рівняння x2 – 2ax + a2 – 4 = 0 менші від числа 5?
6.48.* При яких значеннях a корені рівняння
x2 – (4a – 2) x + 3a2 – 4a + 1 = 0
належать проміжку [–2; 8]?
6.49.* При яких значеннях a один із коренів рівняння
3x2 – (2a + 5) x + 2 + a – a2 = 0
менший від –2, а другий — більший за 3?
![]() ВПРаВи дЛЯ ПоВтоРеннЯ
ВПРаВи дЛЯ ПоВтоРеннЯ
6.50. Розв’яжіть рівняння:
x2 3x+ 4 5 8
![]() 1) x2 − 16 = x2 − 16; 2) x− 3 − x = 3.
1) x2 − 16 = x2 − 16; 2) x− 3 − x = 3.
6.51. Спростіть вираз:
1) 0,5 24 − 4 40 − 150 + 54 + 1000;
2) 8b + 0 3, 50b − 3 2b;
3) 1,5 72 − 216 − 0 6, 450 + 0 5, 96.
6.52. Виразіть із даної рівності змінну x через інші змінні:
![]() 1) 2x −
1) 2x − ![]() m = 2; 2) 1 − 1 = 1 . n m x n
m = 2; 2) 1 − 1 = 1 . n m x n
6.53. Відомо, що a — парне число, b — непарне, a > b. Значення якого з даних виразів може бути цілим числом:
![]()
![]() a b a b a b 1) + ; 2) − ; 3)
a b a b a b 1) + ; 2) − ; 3) ![]() ; 4)
; 4) ![]() ? b a b a b a
? b a b a b a
¿ 6.54. Скільки кілограмів солі міститься в 40 кг 9-відсоткового розчину?
¿ 6.55. Руда містить 8 % олова. Скільки потрібно взяти кілограмів руди, щоб отримати 72 кг олова?
¿ 6.56. Який відсотковий вміст солі в розчині, якщо в 350 г розчину міститься 21 г солі?
ЗаВданнЯ № 1 «ПеРеВіРте Себе» В теСтоВій фоРМі
1. Порівняйте числа a і b, якщо a – b = –3,6.
А) a > b;
Б) a < b;
В) a = b;
Г) порівняти неможливо.
2. Відомо, що m > n. Яке з наведених тверджень хибне?
А) m – 2 > n – 2;
Б) 2m > 2n;
В) m + 2 > n + 2;
Г) –2m > –2n.
3. Оцініть периметр P рівностороннього трикутника зі стороною a см, якщо 0,8 < a < 1,2.
А) 1,6 см < P < 2,4 см;
Б) 2,4 см < P < 3,6 см; В) 3,2 см < P < 4,8 см;
Г) 1,2 см < P < 1,8 см.
4. Відомо, що 2 < x < 3 і 1 < y < 4. Оцініть значення виразу xy.
А) 4 < xy < 8;
Б) 3 < xy < 7;
В) 2 < xy < 12;
Г) 6 < xy < 14.
5. Відомо, що –18 < y < 12. Оцініть значення виразу ![]() y + 2.
y + 2.
А) −3 < 1 y + 2 < 4;
6
![]() Б) −1 < 1 y + 2 < 4;
Б) −1 < 1 y + 2 < 4;
6
В) −1 < 1 y + 2 < 2;
Г) −3 < ![]() y + 2 < 2.
y + 2 < 2.
6. Дано: a > 0, b < 0. Яка з наведених нерівностей може бути правильною?
|
А) a2 < b2; |
В) a – b < 0; |
|
a Б) |
Г) a2b3 > 0. |
b
Завдання № 1 «Перевірте себе» в тестовій формі
7. Множиною розв’язків якої з наведених нерівностей є множина дійсних чисел?
А) 2x > –2; В) 0x > –2;
Б) 2x > 0; Г) 0x > 0.
8. Множиною розв’язків якої з наведених нерівностей є проміжок (3; +∞)?
А) xl 3; В) x > 3;
Б) xm3; Г) x < 3.
x 1
9. ![]() Знайдіть розв’язки нерівності m .
Знайдіть розв’язки нерівності m .
4 5
4 4
А) xl![]() ; В) xm
; В) xm![]() ;
;
Б) xl![]() ; Г) xm
; Г) xm![]() .
.
10. Розв’яжіть нерівність −3x + 8 l 5.
А) xm1; В) xm−1;
Б) xl1; Г) xl −1.
11. ![]() Знайдіть найменший цілий розв’язок нерівності 3x− 5 > 8 −x.
Знайдіть найменший цілий розв’язок нерівності 3x− 5 > 8 −x.
2 3
А) 2; В) 4;
Б) 3; Г) визначити неможливо.
12. ![]() Чому дорівнює добуток натуральних чисел, які належать області визначення виразу 14 − 3x ?
Чому дорівнює добуток натуральних чисел, які належать області визначення виразу 14 − 3x ?
А) 4; В) 18;
Б) 10; Г) 24.
13. Яка з наведених систем нерівностей не має розв’язків?
xl −3, xl −3,
А) xm−2; В) xm−3;
x > −3, xl −2,
Б) x > −2; Г) xm−3.
14. Знайдіть множину розв’язків системи нерівностей
x − 1 > 2x − 3,
4x + 5 > x + 17.
|
А) ∅; |
В) (–∞; 4); |
|
Б) (2; +∞); |
Г) (2; 4). |
15. Який із зображених числових проміжків відповідає множині
8 − 7x > 3x− 2,
розв’язків системи нерівностей −2 3( x− 2 6, ) m−2 (−2 6, )?
А) В)
![]()
0 1 1
Б) Г)
![]()
0 0 1
16. Скільки цілих розв’язків має система нерівностей
![]() x − x− 2 l x− 3 − x− 1,
x − x− 2 l x− 3 − x− 1,
3 4 2
1 − 0 5, x x> − 4?
А) 3; В) 5;
Б) 4; Г) 6.
17. Розв’яжіть нерівність −3 < 1![]() − 2x − 2 < 1.
− 2x − 2 < 1.
5
А) (–3; 7); В) (–7; –3);
Б) (–7; 3); Г) (3; 7).
18. При яких значеннях a рівняння 2x2 + 6x + a = 0 не має коренів? А) a < 4,5; В) a > –4,5;
Б) a > 4,5; Г) a < –4,5.
Головне в параграфі 1
 ! гоЛоВне В ПаРагРафі 1
! гоЛоВне В ПаРагРафі 1
Порівняння чисел
Число a вважають більшим за число b, якщо різниця a – b є додатним числом.
Число a вважають меншим від числа b, якщо різниця a – b є від’ємним числом.
Основні властивості числових нерівностей
Якщо a > b і b > c, то a > c.
Якщо a > b і c — будь-яке число, то a + c > b + c.
Якщо a > b і c — додатне число, то ac > bc.
Якщо a > b і c — від’ємне число, то ac < bc.
1 1
![]() Якщо a > b і ab > 0, то < .
Якщо a > b і ab > 0, то < .
a b
Додавання і множення числових нерівностей
Якщо a > b і c > d, то a + c > b + d.
Якщо a > b, c > d і a, b, c, d — додатні числа, то ac > bd.
Розв’язок нерівності з однією змінною
Розв’язком нерівності з однією змінною називають значення змінної, яке перетворює її в правильну числову нерівність.
Рівносильні нерівності
Нерівності називають рівносильними, якщо вони мають одну й ту саму множину розв’язків.
Правила розв’язування нерівностей з однією змінною
• Якщо який-небудь доданок перенести з однієї частини нерівності в другу, змінивши при цьому його знак на протилежний, то отримаємо нерівність, рівносильну даній.
• Якщо обидві частини нерівності помножити (поділити) на одне й те саме додатне число, то отримаємо нерівність, рівносильну даній.
• Якщо обидві частини нерівності помножити (поділити) на одне й те саме від’ємне число, змінивши при цьому знак нерівності на протилежний, то отримаємо нерівність, рівносильну даній.
Розв’язування системи нерівностей з однією змінною
Розв’язком системи нерівностей з однією змінною називають значення змінної, яке перетворює кожну нерівність системи в правильну числову нерівність.
Розв’язати систему нерівностей означає знайти всі її розв’язки або довести, що розв’язків немає, тобто знайти множину її розв’язків.
Числові проміжки
|
Нерівність |
Проміжок |
Зображення |
|
x > a |
(a; +∞) |
|
|
x < a |
(–∞; a) |
|
|
x al |
[a; +∞) |
|
|
x am |
(–∞; a] |
|
|
a x bm m |
[a; b] |
|
|
a < x < b |
(a; b) |
|
|
a x b< m |
(a; b] |
|
|
a x bm < |
[a; b) |
|
§ 2 квадратичНа фуНкція
• У цьому параграфі ви повторите й розширите свої знання про функцію та її властивості.
• ![]() Навчитеся, використовуючи графік функції y = f (x), будувати графіки функцій y = kf (x), y = f (x) + b, y = f (x + a). • Дізнаєтесь, яку функцію називають квадратичною, яка фігура є її графіком, вивчите властивості квадратичної функції.
Навчитеся, використовуючи графік функції y = f (x), будувати графіки функцій y = kf (x), y = f (x) + b, y = f (x + a). • Дізнаєтесь, яку функцію називають квадратичною, яка фігура є її графіком, вивчите властивості квадратичної функції.
• Навчитеся застосовувати властивості квадратичної функції.
• розширите свої знання про системи рівнянь із двома змінними, методи їхнього розв’язування, набудете нових навичок розв’язування систем рівнянь.
 7. Повторення та розширення відомостей про функцію
7. Повторення та розширення відомостей про функцію
У повсякденному житті нам часто доводиться спостерігати процеси, у яких зміна однієї величини (незалежної змінної) призводить до зміни другої величини (залежної змінної). Вивчення цих процесів потребує створення їхніх математичних моделей. Однією з таких найважливіших моделей є функція.
Із цим поняттям ви ознайомилися в 7 класі. Нагадаємо й уточнимо основні відомості.
Нехай X — множина значень незалежної змінної, Y — множина значень залежної змінної. Функція — це правило, за допомогою якого за кожним значенням незалежної змінної з множини X можна знайти єдине значення залежної змінної з множини Y.
Зазвичай незалежну змінну позначають буквою x, залежну — буквою y, функцію (правило) — буквою f. Кажуть, що змінна y функціонально залежить від змінної x. Цей факт позначають так: y = f (x). Незалежну змінну ще називають аргументом функції.
Множину всіх значень, яких набуває аргумент, називають областю визначення функції і позначають D (f) або D (y).
1
![]() Так, областю визначення функції y = є проміжок (0; +×), тобто D (y) = (0; +×).
Так, областю визначення функції y = є проміжок (0; +×), тобто D (y) = (0; +×).
![]() У функціональній залежності кожному значенню аргументу x відповідає певне значення залежної змінної y. Значення залежної змінної ще називають значенням функції і позначають f (x). Множину всіх значень, яких набуває залежна змінна, називають областю значень функції і позначають E (f) або E (y). Так, областю значень функції y = x є проміжок [0; +×), тобто E (y) = [0; +×).
У функціональній залежності кожному значенню аргументу x відповідає певне значення залежної змінної y. Значення залежної змінної ще називають значенням функції і позначають f (x). Множину всіх значень, яких набуває залежна змінна, називають областю значень функції і позначають E (f) або E (y). Так, областю значень функції y = x є проміжок [0; +×), тобто E (y) = [0; +×).
Функцію вважають заданою, якщо вказано її область визначення та правило, за яким можна за кожним значенням незалежної змінної знайти значення залежної змінної.
Функцію можна задати одним із таких способів:
• описово;
• за допомогою формули; • за допомогою таблиці;
• графічно.
Найчастіше функцію задають за допомогою формули. Такий спосіб задання функції називають аналітичним. Якщо при цьому не вказано область визначення, то вважають, що областю визначення функції є область визначення виразу, який входить до фор-
мули. Наприклад, якщо функцію задано формулою f x( ) = 1 , x− 1
1
![]() то її областю визначення є область визначення виразу , тобx − 1
то її областю визначення є область визначення виразу , тобx − 1
то проміжок (1; +×).
У таблиці наведено функції, які ви вивчали в 7 і 8 класах.
|
Функція |
Область визначення |
Область значень |
Графік |
|
y = kx + b |
(–×; +×) |
Якщо k ≠ 0, то (–×; +×); якщо k = 0, то область значень складається з одного числа b |
Пряма |
|
k y = |
Множина, яка складається з проміжків (–×; 0) і (0; +×) |
Множина, яка складається з проміжків (–×; 0) і (0; +×) |
Гіпербола |
|
y = x2 |
(–×; +×) |
[0; +×) |
Парабола |
|
|
[0; +×) |
[0; +×) |
Вітка параболи |
7. Повторення та розширення відомостей про функцію
1. Що таке функція?
2. ![]() Як позначають той факт, що змінна y функціонально залежить від змінної x?
Як позначають той факт, що змінна y функціонально залежить від змінної x?
3. Що називають аргументом функції?
4. Що називають областю визначення функції?
5. Що називають значенням функції?
6. Що називають областю значень функції?
7. Що треба вказати, щоб функція вважалася заданою?
8. Які способи задання функції ви знаєте?
9. Що вважають областю визначення функції, якщо її задано формулою та при цьому не вказано область визначення?
ВПРаВи
7.1.° Функцію задано формулою f (x) = –2x2 + 5x.
1 1) Знайдіть: f (1); f (0); f ![]() ; f (–5).
; f (–5).
2
2) Знайдіть значення аргументу, при яких значення функції дорівнює: 0; 2; –3.
3) Чи є правильною рівність: f (–1) = 7; f (4) = –12?
7.2.° Функцію задано формулою f (x) = 3x – 2.
1) Знайдіть: f (3); f (0); f (–0,2); f (1,6).
2) Знайдіть значення x, при якому: f (x) = 10; f (x) = –6; f (x) = 0.
7.3.° Кожному натуральному числу, більшому за 10, але меншому від 20, поставили у відповідність остачу при діленні цього числа на 5.
1) Яким способом задано цю функцію?
2) Яка область значень цієї функції?3) Задайте цю функцію таблично.
7.4.° Функцію задано формулою y = 0,4x – 2. Заповніть таблицю відповідних значень x і y:
|
x |
2 |
|
–2,5 |
|
|
y |
|
–2 |
|
0,8 |
Рис. 7.1
7.5.° Дано функцію y = −16![]() . Заповніть таблицю відповідних знаx
. Заповніть таблицю відповідних знаx
чень x і y:
|
x |
2 |
|
–0,4 |
|
|
y |
|
0,8 |
|
–32 |
7.6.° На рисунку 7.1 зображено графік функції y = f (x), визначеної на проміжку [–4; 5]. Користуючись графіком, знайдіть: 1) f (–3,5); f (–2,5); f (–1); f (2);
2) значення x, при яких f (x) = –2,5; f (x) = –2; f (x) = 0; f (x) = 2; 3) область значень функції.
7.7.° На рисунку 7.2 зображено графік функції y = f (x), визначеної на проміжку [–4; 4]. Користуючись графіком, знайдіть:
1) f (–4); f (–1); f (1); f (2,5);
2) значення x, при яких f (x) = –1; f (x) = 0; f (x) = 2; 3) область значень функції.
Рис. 7.2
7. Повторення та розширення відомостей про функцію
![]()
7.8.° Знайдіть область визначення функції:
1) f (x) = 7x – 15; 5) f x( ) = 1 ;
2) ![]() f x( ) = 8 ; 6) f x( ) =
f x( ) = 8 ; 6) f x( ) =
x+ 5
3) ![]() f x( ) = x− 10; 7) f x( ) =
f x( ) = x− 10; 7) f x( ) =
6
4) f x( ) = x − 9; 8) f x(
7.9.° Знайдіть область визначення функції:
1) f x( ) = x+ 3; 4) f x(
x− 4
2) ![]() f x( ) = x2 9+ 16; 5) f x(
f x( ) = x2 9+ 16; 5) f x(
3) f x( ) = x25−x6+x1+ 8; 6) f x(
7.10.° Побудуйте графік функції:
1) f (x) = –2x + 3; 3) f (x) = 3;
2) f x( ) = − ![]() 1 x; 4) f x( ) = −
1 x; 4) f x( ) = − ![]() 6 .
6 .
4 x
7.11.° Побудуйте графік функції:
1) f x( ) = 4 − ![]() 1 x; 2) f x( ) =
1 x; 2) f x( ) = ![]() 8 .
8 .
3 x
7.12.° Знайдіть, не виконуючи побудови, точки перетину з осями координат графіка функції:
1) f x( ) = 1 x − 7; 3) g (x) = 9 – x2;
6
2) ![]() f x( ) = 20 + 4x; 4) j (x) = x2 + 2x – 3.
f x( ) = 20 + 4x; 4) j (x) = x2 + 2x – 3.
3x− 5
7.13.° Знайдіть, не виконуючи побудови, точки перетину з осями координат графіка функції:
2 x2 − 2
1) h (x) = 9 – 10x; 2) p (x) = 4x + x – 3; 3) s x( ) = ![]() x2 + 2.
x2 + 2.
3x − 1, якщо xm−1,
7.14.• Дано функцію f x( ) = x2 − 5, якщо −1 < x < 4, 11, якщо xl 4.
Знайдіть: 1) f (–3); 2) f (–1); 3) f (2); 4) f (6,4).
6, якщо xm−3,
7. 15.• Побудуйте графік функції f x( ) = x2, якщо −3 < x < 1, x, якщо xl1.
• −![]() x4 , якщо x < −2,
x4 , якщо x < −2,
7.16. Побудуйте графік функції f x( ) = −x, якщо −2 m mx 0,
![]() x, якщо x > 0.
x, якщо x > 0.
7.17.• Знайдіть область визначення функції:
1) ![]() f x( ) = x − 2 + x+ 2; 3) f x( x− 5
f x( ) = x − 2 + x+ 2; 3) f x( x− 5
2) ![]() f x( ) = x ; 4) f x( ) =
f x( ) = x ; 4) f x( ) =
x − 7
7.18.• Знайдіть область визначення функції:
1) f x( ) = x + 4 + 2 ; 2) f x( ) =
x+ 1
7.19.• Знайдіть область значень функції:
1) f x( ) = x − 1; 3) f (x) = –7;
2) f (x) = 5 – x2; 4) f (x) = | x | + 2;
7.20.• Знайдіть область значень функції:
![]() 1) f (x) = x2 + 3; 2) f x( ) = 6 − x;
1) f (x) = x2 + 3; 2) f x( ) = 6 − x;
7.21.• Задайте формулою яку-небудь функцію, областю визначення якої є:
1) множина дійсних чисел, крім чисел 1 і 2;
2) множина всіх чисел, не менших від 5;
3) множина всіх чисел, не більших за 10, крім числа –1;4) множина, яка складається з одного числа –4.
7.22.•• Знайдіть область визначення функції та побудуйте її графік:
1) f x( ) = ![]() x2 +− 16; 2) f x( ) = 12
x2 +− 16; 2) f x( ) = 12![]() 2x−−672x ; 3) f x( ) =
2x−−672x ; 3) f x( ) = ![]() xx22 −− 99. x 4 x
xx22 −− 99. x 4 x
7. 23.•• Знайдіть область визначення функції та побудуйте її графік: x2 + 4x+ 4 x3
1) f x( ) = ![]() ; 2) f x( ) =
; 2) f x( ) = ![]() . x+ 2 x
. x+ 2 x
З історії розвитку поняття функції
![]()
7.24. Розкладіть на множники квадратний тричлен:
1) x2 – x – 12; 3) 6x2 + 11x – 2; 2) –x2 + 2x + 35; 4) ![]() x2 + 3x − 6.
x2 + 3x − 6.
7.25. Обчисліть значення виразу:
1) (103 2) æ10−8; 3) 81−2−æ2 35 ;
![]() 9 −3 3 3 2
9 −3 3 3 2
25 æ5 0 125, æ32
2) ![]() −5 ; 4) −2 .
−5 ; 4) −2 .
5 0 5,
7.26. Ціна двох шаф була однаковою. Ціну першої шафи спочатку підвищили на 20 %, а потім знизили на 10 %. Ціну другої шафи, навпаки, спочатку знизили на 10 %, а потім підвищили на 20 %. Ціна якої шафи стала більшою?
7.27. Відстань між містами A і B становить 120 км. Через 2 год після виїзду з міста A вантажний автомобіль затримався біля залізничного переїзду на 6 хв. Щоби прибути в місто B у запланований час, він збільшив швидкість на 12 км/год. З якою швидкістю рухався автомобіль після затримки?
 УЧиМоСЯ Робити неСтандаРтні кРоки
УЧиМоСЯ Робити неСтандаРтні кРоки
7.28. Натуральне число n має рівно 100 різних натуральних дільників (включаючи 1 і n). Знайдіть їхній добуток.
 З історії розвитку поняття функції
З історії розвитку поняття функції
Означення функції, яким ви користуєтеся на даному етапі вивчення математики, з’явилося порівняно нещодавно — у першій половині ХІХ ст. Воно формувалося більше 200 років під впливом бурхливих суперечок видатних математиків кількох поколінь.
Досліджувати функціональні залежності між величинами почали ще стародавні вчені. Цей пошук знайшов відображення у відкритті формул для обчислення площ і об’ємів деяких фігур. Прикладами табличного задання функцій можуть слугувати астрономічні таблиці вавилонян, стародавніх греків і арабів.

П’єр Ферма Рене Декарт
(1601–1665) (1596–1650)
Проте лише в першій половині ХVІІ ст. своїм відкриттям методу координат видатні французькі математики П’єр Ферма і Рене Декарт заклали основи для виникнення поняття функції. У своїх працях вони досліджували зміну ординати точки залежно від зміни її абсциси.
![]() Значну роль у формуванні поняття функції відіграли роботи великого англійського вченого Ісаака Ньютона. Під функцією він розумів величину, яка змінює своє значення з плином часу.
Значну роль у формуванні поняття функції відіграли роботи великого англійського вченого Ісаака Ньютона. Під функцією він розумів величину, яка змінює своє значення з плином часу.
Термін «функція» (від латин. func tio — здійснення, виконання) запровадив німецький математик Готфрід Вільгельм Лейбніц. Він і його учень, швейцарський математик Йоганн Бернуллі, під функцією розуміли формулу, яка пов’язує одну змінну з іншою, тобто вони ототожнювали функцію з одним зі способів її задання.
Подальшому розвиткові поняття функції багато в чому сприяло з’ясу вання істини в багаторічному спо-
рі видатних математиків Леонарда Ісаак Ньютон Ейлера і Жана Лерона д’Аламбера, (1643–1727)
З історії розвитку поняття функції

Готфрід Вільгельм Лейбніц Йоганн Бернуллі
(1646–1716) (1667–1748)
одним із предметів якого було з’ясування сутності цього поняття. У результаті було сформовано більш загальний погляд на функцію як залежність однієї змінної величини від другої, у якому це поняття жорстко не пов’язувалося зі способом задання функції.

Леонард Ейлер Жан Лерон д’Аламбер
(1707–1783) (1717–1783)
У 30-х рр. ХІХ ст. ідеї Ейлера набули подальшого розвитку в роботах видатних учених: російського математика Миколи Лобачев ського та німецького математика Петера Густава Лежена Діріхле. Саме тоді з’явилося таке означення: змінну величину y називають функцією змінної величини x, якщо кожному значенню величини x відповідає єдине значення величини y.
Микола Лобачевський Петер Діріхле
(1792–1856) (1805–1859)
Таке означення функції можна й сьогодні зустріти в шкільних підручниках. Проте більш сучасний погляд — це трактування функції як правила, за допомогою якого за значенням незалежної змінної можна знайти єдине значення залежної змінної.
Коли на межі ХІХ і ХХ ст. виникла теорія множин і стало зрозумілим, що елементами області визначення та області значень зовсім не обов’язково мають бути числа, то під функцією стали розуміти правило, яке кожному елементу множини X ставить у відповідність єдиний елемент множини Y.

Часто про властивості об’єкта можна робити висновки за його зображенням: фотографією, рентгенівським знімком, рисунком тощо.
«Зображенням» функції може слугувати її графік. Покажемо, як графік функції дає змогу визначити певні її властивості.
Рис. 8.1
На рисунку 8.1 зображено графік деякої функції y = f (x).
Її областю визначення є проміжок [–4; 7], а областю значень — проміжок [–4; 4].
При x = –3, x = 1, x = 5 значення функції дорівнюють нулю.
Означення. Значення аргументу, при якому значення функції дорівнює нулю, називають нулем функції.
Так, числа –3, 1, 5 є нулями даної функції.
Зауважимо, що на проміжках [–4; –3) і (1; 5) графік функції f розташований над віссю абсцис, а на проміжках (–3; 1) і (5; 7] — під віссю абсцис. Це означає, що на проміжках [–4; –3) і (1; 5) функція набуває додатних значень, а на проміжках (–3; 1) і (5; 7] — від’ємних.
Кожний із зазначених проміжків називають проміжком знакосталості функції f.
Означення. Проміжок, на якому функція набуває значень однакового знака, називають проміжком знакосталості функції.
Зазначимо, що, наприклад, проміжок (0; 5) не є проміжком знакосталості даної функції.
Зауваження. Під час пошуку проміжків знакосталості функції прийнято вказувати проміжки максимальної довжини. Наприклад, проміжок (–2; –1) є проміжком знакосталості функції f (рис. 8.1), але до відповіді потрібно включити проміжок (–3; 1), який містить проміжок (–2; –1).
Якщо переміщатися по осі абсцис від –4 до –1, то можна помітити, що графік функції «йде вниз», тобто значення функції зменшуються. Говорять, що на проміжку [–4; –1] функція спадає. Зі збільшенням x від –1 до 3 графік функції «йде вгору», тобто значення функції збільшуються. Говорять, що на проміжку [–1; 3] функція зростає.
Означення. Функцію f називають зростаючою на деякому проміжку, якщо для будьяких двох значень аргументу x1 і x2 із цього проміжку таких, що x2 > x1, виконується нерівність f (x2) > f (x1).
Означення. Функцію f називають спадною на деякому проміжку, якщо для будьяких двох значень аргументу x1 і x2 із цього проміжку таких, що x2 > x1, виконується нерівність f (x2) < f (x1).
Часто використовують і такі формулювання.
Означення. Функцію називають зростаючою на деякому проміжку, якщо для будьяких значень аргументу із цього проміжку більшому значенню аргументу відповідає більше значення функції.
Означення. Функцію називають спадною на деякому проміжку, якщо для будьяких значень аргументу із цього проміжку більшому значенню аргументу відповідає менше значення функції.
Якщо функція зростає на всій області визначення, то її називають зростаючою. Якщо функція спадає на всій області визначення, то її називають спадною.
![]() Наприклад, на рисунку 8.2 зображено графік функції y = x. Ця функція є зростаючою. На рисунку 8.3 зображено графік спадної функції y = –x. На рисунку 8.1 зображено графік функції, яка не є ні зростаючою, ні спадною.
Наприклад, на рисунку 8.2 зображено графік функції y = x. Ця функція є зростаючою. На рисунку 8.3 зображено графік спадної функції y = –x. На рисунку 8.1 зображено графік функції, яка не є ні зростаючою, ні спадною.
Рис. 8.2 Рис. 8.3
![]() Приклад 1 Доведіть, що функція y = x2 спадає на проміжку (–×; 0].
Приклад 1 Доведіть, що функція y = x2 спадає на проміжку (–×; 0].
Розв’язання. Нехай x1 і x2 — довільні значення аргументу з проміжку (–×; 0], причому x2 > x1. Покажемо, що x22 < x12, тобто більшому значенню аргументу відповідає менше значення функції.
Маємо: x2 > x1; звідси –x2 < –x1. Обидві частини останньої нерівності є невід’ємними числами. Тоді за властивістю числових нерівностей можна записати, що (–x2)2 < (–x1)2, тобто x22 < x12. ◄
Зазначимо, що в подібних випадках говорять: проміжок (–×; 0] є проміжком спадання функції y = x2. Аналогічно можна довести, що проміжок [0; +×) є проміжком зростання функції y = x2.
У задачах на пошук проміжків зростання і спадання функції прийнято вказувати проміжки максимальної довжини.
![]() Приклад 2 Доведіть, що функція f x( ) =
Приклад 2 Доведіть, що функція f x( ) = ![]() 1 спадає на кожному x
1 спадає на кожному x
з проміжків (–×; 0) і (0; +×).
Розв’язання. Нехай x1 і x2 — довільні значення аргументу з проміжку (0; +×), причому x2 > x1. Тоді за властивістю числових
1 1
![]() нерівностей < . Отже, дана функція спадає на проміжку x2 x1
нерівностей < . Отже, дана функція спадає на проміжку x2 x1
(0; +×).
Аналогічно можна довести, що функція f (x) спадає на проміжку (–×; 0). ◄
1
Проте не можна стверджувати, що функція f x( ) = ![]() спадає на x
спадає на x
всій області визначення, тобто є спадною. Справді, якщо, напри-
1 1
![]() клад, x1 = –2, x2 = 3, то з нерівності x2 > x1 не випливає, що < .
клад, x1 = –2, x2 = 3, то з нерівності x2 > x1 не випливає, що < .
x2 x1
![]() Приклад 3 Доведіть, що лінійна функція f (x) = kx + b є зростаючою при k > 0 і спадною при k < 0.
Приклад 3 Доведіть, що лінійна функція f (x) = kx + b є зростаючою при k > 0 і спадною при k < 0.
Розв’язання. Нехай x1 і x2 — довільні значення аргументу, причому x2 > x1.
Маємо: f (x2) – f (x1) = (kx2 + b) – (kx1 + b) = kx2 – kx1 = k (x2 – x1).
Оскільки x2 > x1, то x2 – x1 > 0.
Тоді якщо k > 0, то k (x2 – x1) > 0, тобто f (x2) > f (x1). Отже, при k > 0 дана функція є зростаючою.
Якщо k < 0, то k (x2 – x1) < 0, тобто f (x2) < f (x1). Отже, при k < 0 дана функція є спадною. ◄

8.1.° На рисунку 8.4 зображено графік функції y = f (x), визначеної на множині дійсних чисел. Користуючись графіком, знайдіть: 1) нулі функції;
2) при яких значеннях аргументу значення функції є додатними; 3) проміжки зростання та проміжки спадання функції.
8.2.° На рисунку 8.5 зображено графік функції y = f (x), визначеної на множині дійсних чисел. Користуючись графіком, знайдіть: 1) нулі функції;
2) при яких значеннях аргументу значення функції є від’ємними; 3) проміжки зростання та проміжки спадання функції.
8.3.° На рисунку 8.6 зображено графік функції, визначеної на проміжку [–1; 4]. Користуючись графіком, знайдіть:
1) нулі функції;
2) при яких значеннях x значення функції є від’ємними; 3) проміжки зростання та проміжки спадання функції.
Рис. 8.6 Рис. 8.7
8.4.° На рисунку 8.7 зображено графік функції y = f (x), визначеної на множині дійсних чисел. Які з даних тверджень є правильними:
1) функція спадає на проміжку (–×; –9]; 2) f (x) < 0 при −5 m mx 1;
3) функція зростає на проміжку [–2; +×);
4) f (x) = 0 при x = –5 і при x = 1;
5) функція на області визначення набуває найменшого значення при x = –2?
![]() 8.5.° На рисунку 8.8 зображено графік функції y = f (x), визначеної на множині дійсних чисел. Користуючись графіком, знайдіть:
8.5.° На рисунку 8.8 зображено графік функції y = f (x), визначеної на множині дійсних чисел. Користуючись графіком, знайдіть:
1) нулі функції;
2) значення x, при яких y < 0; 3) проміжок спадання функції; 4) область значень функції.
Рис. 8.8
8.6.° Зростаючою чи спадною є функція:
1) y = 9x – 4; 3) y = 12 – 3x; 5) y = ![]() x; 2) y = –4x + 10; 4) y = –x; 6) y = 1 – 0,3x?
x; 2) y = –4x + 10; 4) y = –x; 6) y = 1 – 0,3x?
8.7.° Знайдіть нулі функції:
|
1) f (x) = 0,2x + 3; |
4) h x( ) = |
|
2) g (x) = 35 – 2x – x2; |
5) f (x) = x3 – 4x; |
|
8.8.° Знайдіть нулі функції: |
6) f (x) = x2 + 1. |
x2 − −x 6
1) f x( ) = ![]() x + 12; 4) f (x) = –5;
x + 12; 4) f (x) = –5;
|
2) f (x) = 6x2 + 5x + 1; |
5) f x( ) = |
|
|
6) f (x) = x2 – x. |
8.9.° Знайдіть проміжки знакосталості функції:
1) y = 5x – 15; 3) y = x2 – 2x + 1;
2) y = –7x – 28; 4) y = ![]() 9 .
9 .
3 −x
8.10.° Знайдіть проміжки знакосталості функції:
![]() 1) y = –4x + 8; 2) y = –x2 – 1; 3) y = x + 2.
1) y = –4x + 8; 2) y = –x2 – 1; 3) y = x + 2.
8.11.• Накресліть графік якої-небудь функції, визначеної на множині дійсних чисел, нулями якої є числа: 1) –2 і 5; 2) –4, –1, 0 і 4.
8.12.• Накресліть графік якої-небудь функції, визначеної на проміжку [–5; 5], нулями якої є числа –3, 0 і 3.
8.13.• Накресліть графік якої-небудь функції, визначеної на проміжку [–4; 3], такої, що:
1) функція зростає на проміжку [–4; –1] і спадає на проміжку [–1; 3];
2) функція спадає на проміжках [–4; –2] і [0; 3] та зростає на проміжку [–2; 0].
8.14.• Накресліть графік якої-небудь функції, визначеної на множині дійсних чисел, яка зростає на проміжках (–×; 1] і [4; +×) та спадає на проміжку [1; 4].
2x + 8, якщо xm−2,
8.15.• Побудуйте графік функції f x( ) = x2, якщо −2 < x < 2, −2x + 8, якщо xl 2.
Користуючись побудованим графіком, укажіть нулі даної функції, її проміжки знакосталості, проміжки зростання та проміжки спадання.
x4 , якщо x < −1,
![]() 8.16.• Побудуйте графік функції f x( ) = x, якщо − 1 m mx 1,
8.16.• Побудуйте графік функції f x( ) = x, якщо − 1 m mx 1,
4
4
x, якщо x > 1.
Користуючись побудованим графіком, укажіть нулі даної функції, її проміжки знакосталості, проміжки зростання та проміжки спадання.
8.17.• При яких значеннях a функція y = x2 + (2a – 1) x + a2 + a має два нулі?
8.18.• При яких значеннях a функція y = x2 + 6x + a не має нулів?
8.19.• При якому найбільшому цілому значенні n функція y = = (8 – 3n) x – 7 є зростаючою?
8.20.• При яких значеннях m функція y = mx – m – 3 + 2x є спадною?
8.21.• Функція y = f (x) є спадною. Зростаючою чи спадною є функція (відповідь обґрунтуйте):
1) y = 3f (x); 2) y = ![]() f x( ); 3) y = –f (x)?
f x( ); 3) y = –f (x)?
8.22.• Функція y = f (x) зростає на деякому проміжку. Зростаючою чи спадною на цьому проміжку є функція (відповідь обґрун-
туйте):
1) y = ![]() f x( ); 2) y = –2f (x)?
f x( ); 2) y = –2f (x)?
8.23.•• Доведіть, що функція:
1) y = ![]() 6 зростає на проміжку (3; +×);
6 зростає на проміжку (3; +×);
3 −x
2) y = x2 – 4x + 3 спадає на проміжку (–×; 2].
8. 24.•• Доведіть, що функція:
1) y = ![]() 7 спадає на проміжку (–5; +×); x+ 5
7 спадає на проміжку (–5; +×); x+ 5
2) y = 6x – x2 зростає на проміжку (–×; 3].
•• k
8.25. Доведіть, що функція y = ![]() спадає на кожному з проміжків x
спадає на кожному з проміжків x
(–×; 0) і (0; +×) при k > 0 та зростає на кожному із цих проміжків при k < 0.
8.26.* При яких значеннях a функція f (x) = (a – 1) x2 + 2ax + 6 – a має єдиний нуль?
8.27.* Побудуйте графік функції f (x) = x2, визначеної на проміжку [a; 2], де a < 2. Для кожного значення a знайдіть найбільше і найменше значення функції.
![]() ВПРаВи дЛЯ ПоВтоРеннЯ
ВПРаВи дЛЯ ПоВтоРеннЯ
8.28. Скоротіть дріб:
![]() x2 + −x 6 m2 − 16m+ 63 1) ; 3)
x2 + −x 6 m2 − 16m+ 63 1) ; 3) ![]() m2 − 81 ; 2) ; 4)
m2 − 81 ; 2) ; 4) ![]() .
.
|
8.29. Виконайте множення: |
|
|
1) ( 11 + 6 )( 11 − 6 ); 2) |
|
8.30. Два екскаватори різних моделей вирили котлован за 8 год. Перший екскаватор, працюючи самостійно, може вирити такий котлован у 4 рази швидше, ніж другий. За скільки годин може вирити такий котлован кожний екскаватор, працюючи самостійно?
¿ 8.31. До розчину масою 200 г, який містив 12 % солі, додали 20 г солі. Яким став відсотковий вміст солі в новому розчині?
 9. Як побудувати графік функції y = kf (x), якщо відомо графік функції y = f (x)
9. Як побудувати графік функції y = kf (x), якщо відомо графік функції y = f (x)
![]() У 8 класі ви ознайомилися з функцією y = x2 і дізналися, що її графіком є фігура, яку називають параболою (рис. 9.1).
У 8 класі ви ознайомилися з функцією y = x2 і дізналися, що її графіком є фігура, яку називають параболою (рис. 9.1).
Покажемо, як за допомогою графіка функції y = x2 побудувати графік функції y = ax2, де a ≠ 0.
Побудуємо, наприклад, графік функції y = 2x2.
Складемо таблицю значень функцій y = x2 і y = 2x2 при одних і тих самих
значеннях аргументу: Рис. 9.1
|
x |
–3 |
–2,5 |
–2 |
–1,5 |
–1 |
–0,5 |
0 |
0,5 |
1 |
1,5 |
2 |
2,5 |
3 |
|
y = x2 |
9 |
6,25 |
4 |
2,25 |
1 |
0,25 |
0 |
0,25 |
1 |
2,25 |
4 |
6,25 |
9 |
|
y = 2x2 |
18 |
12,5 |
8 |
4,5 |
2 |
0,5 |
0 |
0,5 |
2 |
4,5 |
8 |
12,5 |
18 |
Ця таблиця підказує, що кожній точці (x0; y0) графіка функції y = x2 відповідає єдина точка (x0; 2y0) графіка функції y = 2x2.
А кожна точка (x1; y1) графіка функції y = 2x2 є відповідною єдиній y1 графіка функції y = x2. Тому всі точки графіка функ-
точці x1; 2
ції y = 2x2 можна отримати, замінивши кожну точку графіка функції y = x2 на точку з тією самою абсцисою та з ординатою, помноженою на 2 (рис. 9.2).
Використовуючи графік функції y = x2, побудуємо графік функції y = ![]() x2.
x2.
Зрозуміло, що всі точки графіка функції y = ![]() x2 можна отримати, замінивши кожну точку графіка функції y = x2 на точку з тією самою абсцисою та з ординатою, помноженою на
x2 можна отримати, замінивши кожну точку графіка функції y = x2 на точку з тією самою абсцисою та з ординатою, помноженою на ![]()
(рис. 9.3).
Розглянуті приклади підказують, як, використовуючи графік функції y = f (x), можна побудувати графік функції y = kf (x), де k > 0.
Графік функції y =kf (x), де k > 0, можна отримати, замінивши кожну точку графіка функції y =f (x) на точку з тією самою абсцисою та з ординатою, помноженою на k.
На рисунках 9.4, 9.5 показано, як «працює» це правило для
Говорять, що графік функції y = kf (x) отримано з графіка функції y = f (x) у результаті розтягнення в k разів від осі абсцис, якщо
k > 1, або в результаті стискання в ![]() 1 раза до осі абсцис, якщо k 0 < k < 1.
1 раза до осі абсцис, якщо k 0 < k < 1.
3
Так, графік функції y = ![]() отримано в результаті розтягнення x
отримано в результаті розтягнення x
1
графіка функції y = ![]() у 3 рази від осі абсцис, а графік функції x
у 3 рази від осі абсцис, а графік функції x
![]()
![]() y =
y = ![]() x отримано в результаті стискання графіка функції y = x
x отримано в результаті стискання графіка функції y = x
у 3 рази до осі абсцис.
Розглянемо функції y = x2 і y = –x2. Кожній точці (x0; y0) графіка функції y = x2 відповідає єдина точка (x0; –y0) графіка функції y = –x2. А кожна точка (x1; y1) графіка функції y = –x2 є відповідною єдиній точці (x1; –y1) графіка функції y = x2. Тому всі точки графіка функції y = –x2 можна отримати, замінивши кожну точку графіка функції y = x2 на точку з тією самою абсцисою та з ординатою, помноженою на –1 (рис. 9.6).
Тепер стає зрозумілим, що правило побудови графіка функції y = kf (x), де k < 0, є таким самим, як і для випадку, коли k > 0.
Наприклад, на рисунку 9.7 показано, як можна за допомогою графіка функції y = x2 побудувати графік функції y = −![]() x2.
x2.
![]() Рисунок 9.8 ілюструє, як за допомогою графіка функції y = x можна побудувати графіки функцій
Рисунок 9.8 ілюструє, як за допомогою графіка функції y = x можна побудувати графіки функцій  y = − x і y = −2 x.
y = − x і y = −2 x.
Зауважимо, що при k ≠ 0 функції y = f (x) і y = kf (x) мають одні й ті самі нулі. Отже, графіки цих функцій перетинають вісь абсцис в одних і тих самих точках. Цей факт проілюстровано на рисунку 9.9.
Рис. 9.9
Рис. 9.10
На рисунку 9.10 зображено графіки функцій y = ax2 при деяких значеннях a. Кожний із цих графіків, як і графік функції y = x2, називають параболою. Точка (0; 0) є вершиною кожної із цих парабол.
Якщо a > 0, то вітки параболи напрямлені вгору, якщо a < 0, то вітки параболи напрямлені вниз.
Часто замість вислову «Дано функцію y = ax2» уживають вислів «Дано параболу y = ax2».
У таблиці наведено властивості функції y = ax2, a ≠ 0.
|
Властивість |
a > 0 |
a < 0 |
|
Область визначення |
(–×; +×) |
(–×; +×) |
|
Область значень |
[0; +×) |
(–×; 0] |
|
Нулі функції |
x = 0 |
x = 0 |
|
Проміжки знакосталості |
y > 0 на кожному з проміжків (–×; 0) і (0; +×) |
y < 0 на кожному з проміжків (–×; 0) і (0; +×) |
|
Зростає на проміжку |
[0; +×) |
(–×; 0] |
|
Спадає на проміжку |
(–×; 0] |
[0; +×) |
1. Як можна отримати графік функції y = kf (x), де k≠ 0, використову ючи графік функції y = f (x)?
2. Яка фігура є графіком функції y = ax2, де a ≠ 0?
3. Яка точка є вершиною параболи y = ax2?
4. Як напрямлені вітки параболи y = ax2 при a > 0? при a < 0?
5. Яка область визначення функції y = ax2, де a ≠ 0?
6. Яка область значень функції y = ax2 при a > 0? при a < 0?
7. ![]() На якому проміжку зростає, а на якому проміжку спадає функція y = ax2 при a > 0? при a < 0?
На якому проміжку зростає, а на якому проміжку спадає функція y = ax2 при a > 0? при a < 0?
![]()
![]() 9.1.° Чи належить графіку функції y = –25x2 точка: − 1; −1; 1) A (2; –100); 3) C
9.1.° Чи належить графіку функції y = –25x2 точка: − 1; −1; 1) A (2; –100); 3) C
5
2) B (–2; 100); 4) D (–1; 25)?
9.2.° У яких координатних чвертях знаходиться графік функції y = ax2 при a > 0? при a < 0?
9.3.° Не виконуючи побудови, знайдіть координати точок перетину параболи y = 3x2 і прямої:
1) y = 300; 3) y = –150x; 2) y = 42x; 4) y = 6 – 3x.
9.4.° Не виконуючи побудови, знайдіть координати точок перетину графіків функцій:
1) y = ![]() x2 і y = 3; 2) y =
x2 і y = 3; 2) y = ![]() x2 і y = x + 4.
x2 і y = x + 4.
9.5.° При яких значеннях a точка A (a; 16) належить графіку функції y = 4x2?
9.6.° При яких значеннях b точка B (–2; b) належить графіку функції y = –0,2x2?
9.7.° Відомо, що точка M (3; –6) належить графіку функції y = ax2. Знайдіть значення a.
9.8.° Відомо, що точка K (–5; 10) належить графіку функції y = ax2.
Знайдіть значення a.
9.9.• На рисунку 9.11 зображено графік функції y = ax2. Знайдіть значення a.
а б
Рис. 9.11
9.10.• На рисунку 9.12 зображено графік функції y = ax2. Знайдіть значення a.
а б
Рис. 9.12
9.11.• На рисунку 9.13 зображено графік функції y = f (x). Побудуйте графік функції:
1) y = ![]() f x( ); 2) y = –f (x); 3) y = –2f (x).
f x( ); 2) y = –f (x); 3) y = –2f (x).
9.12.• На рисунку 9.14 зображено графік функції y = g (x). Побудуйте графік функції:
1) y = ![]() g x( ); 2) y = −
g x( ); 2) y = −![]() g x( ).
g x( ).
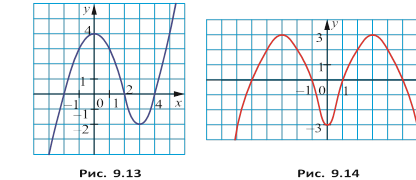
9.13.• Побудуйте графік функції y = x2. Використовуючи цей графік, побудуйте графік функції:
1) y = 3x2; 2) y = −![]() x2.
x2.
![]() 9.14.• Побудуйте графік функції y = x. Використовуючи цей графік, побудуйте графік функції:
9.14.• Побудуйте графік функції y = x. Використовуючи цей графік, побудуйте графік функції:
![]() 1) y = 4 x; 2) y = − x.
1) y = 4 x; 2) y = − x.
9.15.• Доведіть, що функція y = ax2 при a > 0 спадає на проміжку (–×; 0] і зростає на проміжку [0; +×).
9.16.• Доведіть, що функція y = ax2 при a < 0 зростає на проміжку (–×; 0] і спадає на проміжку [0; +×).
9.17.• Побудуйте графік функції: x2, якщо xm−2, y = −2x, якщо −2 < x < 2, −x2, якщо xl 2.
Користуючись побудованим графіком, знайдіть проміжки зростання та проміжки спадання функції.
9. 18.• Побудуйте графік функції: −2, якщо x < −1, y = −2x2, якщо −1 m mx 0, 2x2, якщо x > 0.
Користуючись побудованим графіком, знайдіть проміжки зростання та проміжки спадання функції.
![]()
9.19. Доведіть тотожність:
![]() mm n2 +− − m 2 : m3 −n2mn2 + m n1+ = n m−n .
mm n2 +− − m 2 : m3 −n2mn2 + m n1+ = n m−n .
mn mn n+
9.20. Спростіть вираз:
2 (m− 5)4
1) ![]() (a b− ) , якщо b al ; 3) 2 ;
(a b− ) , якщо b al ; 3) 2 ;
m − 10m+ 25
2 x2 − 2x+ 1
2) c + 6c + 9, якщо cl −3; 4) , якщо x < 1.
(x− 1)6
9.21. Для перевезення 45 т вантажу планували взяти автомобіль певної вантажопідйомності. Проте через його несправність довелося взяти інший автомобіль, вантажопідйомність якого на 2 т менша, ніж першого. Через це знадобилося зробити на 6 рейсів більше, ніж було заплановано. Знайдіть вантажопідйомність автомобіля, який перевіз вантаж.
9.22. Якого найменшого значення може набути даний вираз і при якому значенні змінної:
1) (x – 6)2 + 3; 3) x2 + 2x – 6; 2) (x + 4)2 – 5; 4) x2 – 10x + 18?
 УЧиМоСЯ Робити неСтандаРтні кРоки
УЧиМоСЯ Робити неСтандаРтні кРоки
9.23. Щоби пофарбувати одну грань кубика, потрібно 10 с. За який найменший час 6 людей можуть пофарбувати 101 кубик? (Двоє людей не можуть одночасно фарбувати один кубик.)
 10. Як побудувати графіки функцій y = f (x) + b і y = f (x + a), якщо відомо графік функції y = f (x)
10. Як побудувати графіки функцій y = f (x) + b і y = f (x + a), якщо відомо графік функції y = f (x)
Покажемо, як, використовуючи графік функції y = x2, можна побудувати графік функції y = x2 + 2.
Складемо таблицю значень цих функцій при одних і тих самих значеннях аргументу.
|
x |
–3 |
–2,5 |
–2 |
–1,5 |
–1 |
–0,5 |
0 |
0,5 |
1 |
1,5 |
2 |
2,5 |
3 |
|
y = x2 |
9 |
6,25 |
4 |
2,25 |
1 |
0,25 |
0 |
0,25 |
1 |
2,25 |
4 |
6,25 |
9 |
|
y = x2 + 2 |
11 |
8,25 |
6 |
4,25 |
3 |
2,25 |
2 |
2,25 |
3 |
4,25 |
6 |
8,25 |
11 |
Ця таблиця підказує, що кожній точці (x0; y0) графіка функції y = x2 відповідає єдина точка (x0; y0 + 2) графіка функції y = x2 + 2. А кожна точка (x1; y1) графіка функції y = x2 + 2 є відповідною єдиній точці (x1; y1 – 2) графіка функції y = x2. Тому всі точки графіка функції y = x2 + 2 можна отримати, замінивши кожну точку графіка функції y = x2 на точку з тією самою абсцисою та з ординатою, збільшеною на 2 (рис. 10.1).
Говорять, що графік функції y = x2 + 2 отримано в результаті паралельного перенесення[1] графіка функції y = x2 на дві одиниці вгору вздовж осі ординат.
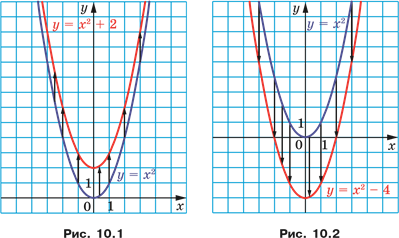
Аналогічно, графік функції y = x2 – 4 можна отримати в результаті паралельного перенесення графіка функції y = x2 на 4 одиниці вниз уздовж осі ординат (рис. 10.2).
Ці приклади підказують, як можна, використовуючи графік функції y = f (x), побудувати графік функції y = f (x) + b.
Графік функції y =f (x) +b можна отримати в результаті паралельного перенесення графіка функції y = f (x) уздовж осі ординат на b одиниць угору, якщо b > 0, і на –b одиниць униз, якщо b < 0.
На рисунках 10.3, 10.4 показано, як «працює» це правило для
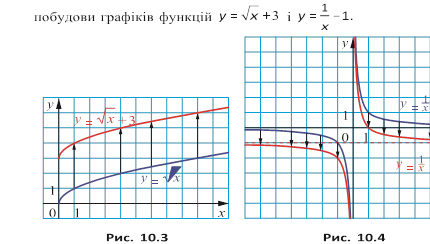
Очевидно, що в результаті паралельного перенесення отримуємо фігуру, яка дорівнює фігурі, що є графіком початкової функції. Наприклад, кожний із графіків функцій y = x2 + 2 і y = x2 – 4 дорівнює параболі y = x2. Тому графіками функцій y = x2 + 2 і y = x2 – 4 також є параболи.
Покажемо, як можна за допомогою графіка функції y = x2 побудувати графік функції y = (x + 2)2.
Нехай точка (x0; y0) належить графіку функції y = x2, тобто x02 = y0. Доведемо, що точка (x0 – 2; y0) належить графіку функції y = (x + 2)2. Знайдемо значення цієї функції у точці з абсцисою x0 – 2. Маємо: ((x0 – 2) + 2)2 = x02 = y0. Отже, кожній точці (x0; y0) графіка функції y = x2 відповідає єдина точка (x0 – 2; y0) графіка функції y = (x + 2)2. Аналогічно можна показати, що кожна точка (x1; y1) графіка функції y = (x + 2)2 є відповідною єдиній точці (x1 + 2; y1) графіка функції y = x2.
Тому всі точки графіка функції y = (x + 2)2 можна отримати, замінивши кожну точку графіка функції y = x2 на точку з тією самою ординатою та з абсцисою, зменшеною на 2 (рис. 10.5).
Говорять, що графік функції y = (x + 2)2 отримано в результаті паралельного перенесення графіка функції y = x2 уздовж осі абсцис на 2 одиниці вліво.
Покажемо, як за допомогою графіка функції y = x2 побудувати графік функції y = (x – 2)2. Легко встановити (зробіть це самостійно), що кожній точці (x0; y0) графіка функції y = x2 відповідає єдина точка (x0 + 2; y0) графіка функції y = (x – 2)2 і кожна точка (x1; y1)
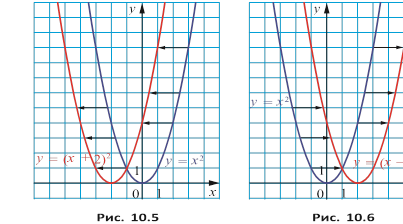
графіка функції y = (x – 2)2 є відповідною єдиній точці (x1 – 2; y1) графіка функції y = x2. Тому графік функції y = (x – 2)2 можна отримати в результаті паралельного перенесення графіка функції y = x2 уздовж осі абсцис на 2 одиниці вправо (рис. 10.6).
Ці приклади підказують, як можна, використовуючи графік функції y = f (x), побудувати графік функції y = f (x + a).
Графік функції y =f (x +a) можна отримати в результаті паралельного перенесення графіка функції y =f (x) уздовж осі абсцис на a одиниць уліво, якщо a > 0, і на –a одиниць управо, якщо a < 0.
На рисунках 10.7, 10.8 показано, як «працює» це правило для
Зауважимо, що графіками функцій y = (x + 2)2 і y = (x – 2)2 є параболи, які дорівнюють параболі y = x2.
![]() Приклад 1 Побудуйте графік функції y = (x – 1)2 + 3.
Приклад 1 Побудуйте графік функції y = (x – 1)2 + 3.
Розв’язання. 1) Побудуємо графік функції y = x2.
2) Паралельно перенесемо графік функції y = x2 уздовж осі абсцис на 1 одиницю вправо. Отримаємо графік функції y = (x – 1)2 (рис. 10.9).
3) Паралельно перенесемо графік функції y = (x – 1)2 уздовж осі ординат на 3 одиниці вгору. Отримаємо графік функції y = = (x – 1)2 + 3 (див. рис. 10.9).
Описаний алгоритм побудови подамо у вигляді такої схеми:
|
y = x2 |
управо на 1 од. |
угору на 3 од. y = (x – 1)2 |
y = (x – 1)2 + 3 |
◄
Рис. 10.9 Рис. 10.10
![]() Приклад 2 Побудуйте графік функції y =
Приклад 2 Побудуйте графік функції y = ![]() (x + 3)2 − 1.
(x + 3)2 − 1.
1 2
Розв’язання. 1) Побудуємо графік функції y = ![]() x (рис. 10.10).
x (рис. 10.10).
2) Паралельно перенесемо графік функції y =![]() x2 уздовж осі абсцис на 3 одиниці вліво. Отримаємо графік функції y =
x2 уздовж осі абсцис на 3 одиниці вліво. Отримаємо графік функції y = ![]() (x + 3)2 (див. рис. 10.10).
(x + 3)2 (див. рис. 10.10).
3) Паралельно перенесемо графік функції y = ![]() (x + 3)2 уздовж осі ординат на 1 одиницю вниз. Отримаємо шуканий графік (див. рис. 10.10).
(x + 3)2 уздовж осі ординат на 1 одиницю вниз. Отримаємо шуканий графік (див. рис. 10.10).
Схема побудови має такий вигляд:
|
|
|
y = |
З описаних перетворень випливає, що графіком функції y =
= ![]() (x + 3)2 − 1 є парабола, яка дорівнює параболі y =
(x + 3)2 − 1 є парабола, яка дорівнює параболі y = ![]() x2 і вершиною
x2 і вершиною
якої є точка (–3; –1). ◄
Із цього прикладу стає зрозумілим алгоритм побудови графіка функції y = kf (x + a) + b, зокрема функції y = k (x + a)2 + b.
Графіком функції y =k (x +a)2+b, k ≠0, є парабола, яка дорівнює параболі y = kx2 і вершиною якої є точка (–a; b).
![]() Приклад 3 Побудуйте графік функції y = –2x2 – 20x – 47.
Приклад 3 Побудуйте графік функції y = –2x2 – 20x – 47.
Розв’язання. Маємо: y = –2x2 – 20x – 47 = –2x2 – 20x –
– 50 + 3 = –2 (x + 5)2 + 3.
Ми представили формулу, що задає дану функцію, у вигляді y = kf (x + a) + b, де f (x) = x2, k = –2, a = 5, b = 3. Схема побудови має такий вигляд:
|
уліво на 5 од. y = –2x2 |
угору на 3 од. y = –2 (x + 5)2 |
y = –2 (x + 5)2 + 3 |
Побудований графік є параболою, яка дорівнює параболі y = –2x2 і вершиною якої є точка (–5; 3) (рис. 10.11). ◄
Рис. 10.11
1. ![]() Як можна отримати графік функції y = f (x) + b, використовуючи графік функції y = f (x)?
Як можна отримати графік функції y = f (x) + b, використовуючи графік функції y = f (x)?
2. Яка фігура є графіком функції y = x2 + b?
3. Які координати вершини параболи y = x2 + b?
4. Як можна отримати графік функції y = f (x + a), використовуючи графік функції y = f (x)?
5. Яка фігура є графіком функції y = (x + a)2?
6. Які координати вершини параболи y = (x + a)2?
7. Яка фігура є графіком функції y = k (x + a)2 + b, де k ≠ 0?
8. Які координати вершини параболи y = k (x + a)2 + b?
ВПРаВи
10.1.° Графік якої функції отримаємо, якщо графік функції y = x2 паралельно перенесемо:
1) на 6 одиниць угору вздовж осі ординат;
2) на 9 одиниць управо вздовж осі абсцис;
3) на 12 одиниць униз уздовж осі ординат;
4) на 7 одиниць уліво вздовж осі абсцис;
5) на 2 одиниці вправо вздовж осі абсцис і на 3 одиниці вниз уздовж осі ординат;
6) на 1 одиницю вліво вздовж осі абсцис і на 1 одиницю вгору вздовж осі ординат?
10.2.° Графік якої з наведених функцій отримаємо, якщо паралельно перенесемо графік функції y = x2 уздовж осі абсцис на 4 одиниці вправо:
1) y = x2 + 4; 2) y = x2 – 4; 3) y = (x + 4)2; 4) y = (x – 4)2?
10.3.° Графік якої з наведених функцій отримаємо, якщо паралельно перенесемо графік функції y = x2 уздовж осі ординат на 5 одиниць угору:
1) y = x2 + 5; 2) y = x2 – 5; 3) y = (x + 5)2; 4) y = (x – 5)2?
10.4.° Які координати має вершина параболи:
1) y = x2 + 8; 5) y = (x – 4)2 + 3;
2) y = x2 – 8; 6) y = (x + 4)2 + 3;
3) y = (x + 8)2; 7) y = (x – 4)2 – 3;
4) y = (x – 8)2; 8) y = (x + 4)2 – 3?
10.5.° У якій координатній чверті знаходиться вершина параболи:
1) y = (x + 10)2 – 16; 3) y = (x + 15)2 + 4;
2) y = (x – 11)2 + 15; 4) y = (x – 11)2 – 9?
5
10.6.° Як треба паралельно перенести графік функції y = ![]() , щоб x
, щоб x
отримати графік функції y = ![]() 5 :
5 :
x− 8
1) на 8 одиниць угору вздовж осі ординат;
2) на 8 одиниць униз уздовж осі ординат;
3) на 8 одиниць управо вздовж осі абсцис;4) на 8 одиниць уліво вздовж осі абсцис?
![]()
![]() 10.7.° Як треба паралельно перенести графік функції y = x, щоб отримати графік функції y = x+ 3:
10.7.° Як треба паралельно перенести графік функції y = x, щоб отримати графік функції y = x+ 3:
1) на 3 одиниці вгору вздовж осі ординат;
2) на 3 одиниці вниз уздовж осі ординат;
3) на 3 одиниці вправо вздовж осі абсцис;4) на 3 одиниці вліво вздовж осі абсцис?
10.8.• На рисунку 10.12 зображено графік функції y = f (x). Побудуйте графік функції:
1) y = f (x) – 2; 3) y = f (x – 3); 5) y = –f (x);
Рис. 10.12
![]() 10.9.• На рисунку 10.13 зображено графік функції y = f (x). Побудуйте графік функції:
10.9.• На рисунку 10.13 зображено графік функції y = f (x). Побудуйте графік функції:
1) y = f (x) + 5; 4) y = f (x – 2);
2) y = f (x) – 3; 5) y = –f (x);
3) y = f (x + 1); 6) y = –f (x) – 1. Рис. 10.13
10.10.• Побудуйте графік функції y = x2. Використовуючи цей графік, побудуйте графік функції:
1) y = x2 – 3; 3) y = (x – 5)2; 5) y = (x – 1)2 + 2; 2) y = x2 + 4; 4) y = (x + 2)2; 6) y = (x + 3)2 – 2.
10.11.• Побудуйте графік функції y = –x2. Використовуючи цей графік, побудуйте графік функції:
1) y = –x2 + 1; 3) y = –(x – 2)2; 5) y = –(x + 1)2 – 1; 2) y = –x2 – 2; 4) y = –(x + 4)2; 6) y = –(x – 3)2 + 4.
10. 12.• Побудуйте графік функції y = − ![]() 6 . Використовуючи цей x
6 . Використовуючи цей x
графік, побудуйте графік функції:
![]() 1) y = −
1) y = − ![]() 6 + 5; 2) y = − 6 ; 3) y = −
6 + 5; 2) y = − 6 ; 3) y = − ![]() 6 − 2. x x− 2 x+ 4
6 − 2. x x− 2 x+ 4
• 2
10.13. Побудуйте графік функції y = . Використовуючи цей граx
|
фік, побудуйте графік функції: |
|
|
1) y = |
3) y = x− 3 |
![]() 10.14.• Побудуйте графік функції y = x. Використовуючи цей графік, побудуйте графік функції:
10.14.• Побудуйте графік функції y = x. Використовуючи цей графік, побудуйте графік функції:
![]()
![]() 1) y = x − 4; 2) y = x − 4; 3) y = x − 1 + 3.
1) y = x − 4; 2) y = x − 4; 3) y = x − 1 + 3.
10.15.• Побудуйте графік функції y = (x + 5)2 – 9. Користуючись графіком, знайдіть:
1) нулі функції;
2) при яких значеннях аргументу функція набуває додатних значень;
3) проміжок зростання та проміжок спадання функції;4) область значень функції.
10.16.• Побудуйте графік функції y = (x – 4)2 + 4. Користуючись графіком, знайдіть:
1) нулі функції;
2) при яких значеннях аргументу функція набуває від’ємних значень;
3) проміжок зростання та проміжок спадання функції;4) область значень функції.
10.17.• Задайте формулою виду y = ax2 + n функцію, графік якої зображено на рисунку 10.14.
10.18.• Задайте формулою виду y = ax2 + n функцію, графік якої зображено на рисунку 10.15.
10.19.• Задайте формулою виду y = a (x + m)2 функцію, графік якої зображено на рисунку 10.16.
а б
Рис. 10.14
а б
Рис. 10.15
а б
Рис. 10.16
10.20.• Задайте формулою виду y = a (x + m)2 функцію, графік якої зображено на рисунку 10.17.
а б
Рис. 10.17
10.21.• Задайте формулою виду y = a (x + m)2 + n функцію, графік якої зображено на рисунку 10.18.
Рис. 10.18
10.22.• Задайте формулою виду y = a (x + m)2 + n функцію, графік якої зображено на рисунку 10.19.
10. 23.• Розв’яжіть графічно рівняння:
![]() 1) (x − 1)2 =
1) (x − 1)2 = ![]() 2 ; 2) 1 − x2 = x − 1.
2 ; 2) 1 − x2 = x − 1.
x
• 3
10.24. Розв’яжіть графічно рівняння = x + 2. x
а б
Рис. 10.19
10.25.• Прямі m і n, зображені на рисунку 10.20, паралельні, причому пряма n є графіком функції y = f (x). Яке з тверджень є правильним:
1) пряма m є графіком функції y = f (x) + b;
2) пряма m є графіком функції y = f (x – a)?
Рис. 10.20
10.26.•• Задайте дану функцію формулою виду y = a (x – m)2 + n і побудуйте її графік, використовуючи графік функції y = ax2: 1) y = x2 – 4x + 6;
2) y = –x2 + 6x – 6;
3) y = 2x2 – 4x + 5; 4) y = 0,2x2 – 2x – 4.
10.27.•• Задайте дану функцію формулою виду y = a (x – m)2 + n і побудуйте її графік, використовуючи графік функції y = ax2: 1) y = x2 – 2x – 8;
2) y = –2x2 + 8x – 3.
10.28.•• Задайте дану функцію формулою виду y = k + b і побуx a+
k
дуйте її графік, використовуючи графік функції y = : x
1) y = ![]() 3x+ 8; 2) y =
3x+ 8; 2) y = ![]() 2x+ 14; 3) y = −2x . x x+ 3 x− 1
2x+ 14; 3) y = −2x . x x+ 3 x− 1
10. ![]() 29.•• Задайте дану функцію формулою виду y = k + b і побуx a+
29.•• Задайте дану функцію формулою виду y = k + b і побуx a+
k
дуйте її графік, використовуючи графік функції y = :
x
|
1) y =
10.30. Спростіть вираз: |
2) y = 7 x− 2 |
|
5a− 3 1) + a+ 9; 8a 4a 5a− 6b 2) ab bc 10.31. Скоротіть дріб: |
8a+ 5b 3) 2 − 2a−27b; 5ab 2a b
4) 4 4 − 5 2 . 8m n 6m n |
![]() 9 + m 5m + 7n
9 + m 5m + 7n
1) ![]() ; 3) ; m− 81 5m + 2 35mn + 7n
; 3) ; m− 81 5m + 2 35mn + 7n
![]() 25m
25m
2) ; 4) + 10n 3m + 3n2 .
5 m n+ 3
10.32. Чисельник звичайного дробу на 1 менший від його знаменника. Якщо чисельник і знаменник дробу зменшити на 1, то значення дробу зменшиться на ![]() . Знайдіть цей дріб.
. Знайдіть цей дріб.
10.33. Доведіть, що при додатних значеннях a і b виконується нерівність a3 + b3 la2b ab+ 2.
 11. квадратична функція, її графік і властивості
11. квадратична функція, її графік і властивості
Означення. Функцію, яку можна задати формулою виду y =ax2 + bx + c, де x — незалежна змінна, a, b і c — деякі числа, причому a ≠0, називають квадратичною.
Квадратична функція не є для вас новою. Так, у 8 класі ви вивчали її окремий випадок, а саме функцію y = x2. Функціональна залежність площі S круга від його радіуса r визначає квадратичну функцію S (r) = pr2, яка є функцією виду y = ax2. Із цією функцією ви ознайомилися в п. 9.
gt2
На уроках фізики ви ознайомилися з формулою h v t= 0 − ![]() ,
,
2
яка задає залежність висоти h, на якій знаходиться тіло, що його кинули вертикально вгору з початковою швидкістю v0, від часу
gt2
руху t. Ця формула задає квадратичну функцію h t( ) = v t0 − ![]() .
.
2
Покажемо, як можна отримати графік квадратичної функції y = ax2 + bx + c із графіка функції y = ax2.
![]()
![]() Ви вже будували графіки функцій виду y = ax2 + bx + c, виділяючи квадрат двочлена (див. приклад 3 п. 10). Використаємо цей прийом у загальному вигляді. Маємо: ax2 + bx c a x+ = 2 + abx + c = a x 2 + 2xæ b + b22 − b22 + ac =
Ви вже будували графіки функцій виду y = ax2 + bx + c, виділяючи квадрат двочлена (див. приклад 3 п. 10). Використаємо цей прийом у загальному вигляді. Маємо: ax2 + bx c a x+ = 2 + abx + c = a x 2 + 2xæ b + b22 − b22 + ac =
a 2a 4a 4a
![]()
![]() = a x + 2ba 2 + 4ac b4a−2 2 = a x + 2ba 2 + 4ac b4a− 2 .
= a x + 2ba 2 + 4ac b4a−2 2 = a x + 2ba 2 + 4ac b4a− 2 .
b 4ac b− 2
Уведемо позначення x0 = − , y0 = .
2a 4a
Тоді формулу y = ax2 + bx + c можна подати у вигляді y = a (x – x0)2 + y0.
Отже, схема побудови шуканого графіка є такою:
|
управо угору або вліво або вниз на | x0 | од. на | y0 | од. y = ax2 |
Рис. 11.1 Рис. 11.2
На рисунку 11.1 показано побудову для випадку, коли a > 0, x0 > 0, y0 < 0. На рисунку 11.2 показано побудову для випадку, коли a < 0, x0 < 0, y0 > 0.
Тепер можна зробити такий висновок: графіком квадратичної функції y = ax2 + bx + c є парабола, яка дорівнює параболі y = ax2,
b 4ac b− 2
з вершиною в точці (x0; y0), де x0 = − ![]() , y0 =
, y0 = ![]() .
.
2a 4a
Вітки параболи y = ax2 + bx + c напрямлені так само, як і вітки параболи y = ax2: якщо a > 0, то вітки параболи напрямлені вгору, якщо a < 0, то вітки параболи напрямлені вниз.
Загальне уявлення про графік квадратичної функції дають координати вершини параболи та напрям її віток. Це уявлення буде тим повнішим, чим більше точок, які належать графіку, ми знатимемо. Тому можна будувати графік квадратичної функції, не використовуючи паралельних перенесень, за такою схемою:
1) знайти абсцису вершини параболи за формулою x0 = − ![]() b ;
b ;
2a
2) знайти ординату вершини параболи за формулою[2]
4ac b− [3] D
![]() y0 = = − ,
y0 = = − ,
4a 4a
де D — дискримінант квадратного тричлена ax2 + bx + c, і позначити на координатній площині вершину параболи;
![]() D
D
3) визначити напрям віток параболи;
4) знайти координати ще кількох точок, які належать шуканому графіку, зокрема координати точок перетину параболи з віссю абсцис (якщо дана функція має нулі), координати точки перетину параболи з віссю ординат; позначити ці точки на координатній площині;
5) провести через усі позначені точки плавну неперервну лінію.
![]() Приклад Побудуйте графік функції f (x) = x2 + 4x – 5. Користуючись графіком функції, знайдіть область її значень, проміжки зростання і спадання, проміжки знакосталості, найменше і найбільше значення функції.
Приклад Побудуйте графік функції f (x) = x2 + 4x – 5. Користуючись графіком функції, знайдіть область її значень, проміжки зростання і спадання, проміжки знакосталості, найменше і найбільше значення функції.
Розв’язання. Дана функція є квадратичною. Її графіком є парабола, вітки якої напрямлені вгору.
Знайдемо абсцису й ординату вершини параболи. Маємо: x0 = −![]() = −2, ордината вершини y0 = f (x0) = f (–2) = –9.
= −2, ордината вершини y0 = f (x0) = f (–2) = –9.
Отже, точка (–2; –9) — вершина параболи.
Знайдемо координати точок перетину параболи з віссю абсцис.
Для цього розв’яжемо рівняння: x2 + 4x – 5 = 0.
Звідси x1 = –5, x2 = 1.
Отже, парабола перетинає вісь абсцис у точках (–5; 0) і (1; 0).
![]() Знайдемо точку перетину параболи з віссю ординат. Маємо: f (0) = –5. Парабола перетинає вісь ординат у точці (0; –5).
Знайдемо точку перетину параболи з віссю ординат. Маємо: f (0) = –5. Парабола перетинає вісь ординат у точці (0; –5).
Позначимо знайдені чотири точки параболи на координатній площині
(рис. 11.3).
Тепер бачимо, що доцільно знайти значення даної функції в точках –1, –3, –4 та позначити відповідні точки на координатній площині.
Маємо: f (–3) = f (–1) = –8; f (–4) = = f (0) = –5.
Сполучимо всі позначені точки плав-
Рис. 11.3 ною неперервною лінією.
Рис. 11.4
Шуканий графік зображено на рисунку 11.4.
Областю значень функції є множина E (f) = [–9; +×).
Функція зростає на проміжку [–2; +×) і спадає на проміжку (–×; –2].
Маємо: f (x) > 0 на кожному з проміжків (–×; –5) і (1; +×); f (x) < 0 на проміжку (–5; 1).
Найменше значення функції дорівнює –9, найбільшого значення не існує. ◄
1. Яку функцію називають квадратичною?
2. Яка фігура є графіком квадратичної функції?
3. ![]() За якою формулою можна знайти абсцису вершини параболи y = = ax2 + bx + c?
За якою формулою можна знайти абсцису вершини параболи y = = ax2 + bx + c?
4. Який напрям мають вітки параболи y = ax2 + bx + cзалежно від значення a?
5. опишіть схему побудови графіка квадратичної функції.
ВПРаВи
11.1.° Які з даних функцій є квадратичними:
1) y = 4x2 + 3x + 6; 3) y = ![]() ; 2) y = 4x + 3; 4) y = 6x2 – 5x?
; 2) y = 4x + 3; 4) y = 6x2 – 5x?
11.2.° Обчисліть значення функції f (x) = 5x2 – 7x + 2, якщо аргумент x дорівнює 1; –2; 4.
11.3.° Дано функцію f (x) = x2 – 2x – 15. Знайдіть значення аргументу x, при якому:
1) f (x) = 0; 2) f (x) = –7; 3) f (x) = 33.
11.4.° Графік функції y = –6x2 + x + c перетинає вісь ординат у точці M (0; –8). Знайдіть значення c.
11.5.° Визначте напрям віток і координати вершини параболи: 1) y = x2 – 12x + 3; 3) y = 0,3x2 + 2,4x – 5; 2) y = –x2 + 4x – 6; 4) y = –5x2 + 10x + 2.
11.6.° Побудуйте графік функції:
1) y = x2 – 4x – 5; 5) y = x2 – 2x + 4; 2) y = –x2 + 2x + 3; 6) y = −![]() x2 + 3x − 4;
x2 + 3x − 4;
|
3) y = 6x – x2; |
7) y = x2 – 6x + 5; |
|
4) y = 2x2 – 8x + 8; |
8) y = 2x2 – 5x + 2. |
11.7.° Побудуйте графік функції:
1) y = x2 + 2x – 8; 3) y = –x2 + 4x – 5; 2) y = x2 – 2x; 4) y = 2x2 – 2x – 4.
11.8.• Побудуйте графік функції f (x) = x2 – 6x + 8. Користуючись графіком, знайдіть:
1) f (6); f (1);
2) значення x, при яких f (x) = 8; f (x) = –1; f (x) = –2;
3) найбільше і найменше значення функції;
4) область значень функції;
5) проміжок зростання та проміжок спадання функції;
6) при яких значеннях аргументу функція набуває додатних значень, а при яких — від’ємних.
11.9.• Побудуйте графік функції f (x) = –x2 – 6x – 5. Користуючись графіком, знайдіть: 1) область значень функції;
2) проміжок зростання функції;
3) множину розв’язків нерівності f (x) > 0.
11.10.• Побудуйте графік функції f (x) = x – 0,5x2. Користуючись графіком, знайдіть: 1) область значень функції;
2) проміжок зростання функції;
3) при яких значеннях x виконується нерівність f x( ) m 0.
11.11.• Побудуйте графік функції f (x) = 3x2 – 6x. Користуючись графіком, знайдіть: 1) область значень функції;
2) проміжок спадання функції;
3) при яких значеннях x виконується нерівність f x( ) l 0.
11.12.• Розв’яжіть графічно рівняння x2 − 3x − 1 = − .
![]() 11.13.• Розв’яжіть графічно рівняння −
11.13.• Розв’яжіть графічно рівняння −![]() x2 + x + 2 = x.
x2 + x + 2 = x.
11.14.• Побудуйте в одній системі координат графіки функцій y = f (x) і y = g (x) та визначте кількість коренів рівняння f (x) = g (x):
1) ![]() f (x) = –x2 + 6x – 7, g x( ) = − x;
f (x) = –x2 + 6x – 7, g x( ) = − x;
2) f (x) = 4x – 2x2, g x( ) = − 4 .
x
11.15.• Побудувавши в одній системі координат графіки функцій
2 6
y = x + 4x + 1 і y = ![]() , визначте кількість коренів рівняння x
, визначте кількість коренів рівняння x
x2 + 4x + 1 = ![]() 6 . x
6 . x
11.16.• Знайдіть координати точки параболи y = –x2 + 9x + 9, у якої:
1) абсциса й ордината рівні;
2) сума абсциси й ординати дорівнює 25.
11.17.• Знайдіть координати точки параболи y = 2x2 – 3x + 6, у якої ордината на 12 більша за абсцису.
11.18.• Знайдіть область значень і проміжки зростання та спадання функції:
1) f (x) = 4x2 – 8x + 3; 3) f (x) = 4 – 12x – 0,3x2;
2) f x( ) = −![]() x2 + 2x − 6; 4) f (x) = 7x2 + 21x.
x2 + 2x − 6; 4) f (x) = 7x2 + 21x.
11.19.• Знайдіть область значень і проміжки зростання та спадання функції:
1) f (x) = 2x2 – 12x + 8; 2) f (x) = 9 + 8x – 0,2x2.
11.20.• Побудуйте графік даної функції, укажіть її область значень і проміжки зростання та спадання:
3 −x, якщо xm−2,
y = x2 − 2x− 3, якщо − <2 x < 2, −3, якщо xl 2.
11.21.• Побудуйте графік даної функції, укажіть її область значень і проміжки зростання та спадання:
x, якщо xm 0,
y = 4x x− 2, якщо 0 < x < 5, x− 10, якщо xl 5.
11.22.• Задайте формулою яку-небудь квадратичну функцію, яка:
1) спадає на проміжку (–×; 1] і зростає на проміжку [1; +×); 2) зростає на проміжку (–×; –2] і спадає на проміжку [–2; +×).
11.23.• Знайдіть найменше значення функції y = 3x2 – 18x + 2 на проміжку:
1) [–1; 4]; 2) [–4; 1]; 3) [4; 5].
11.24.• Знайдіть найбільше значення функції y = –x2 – 8x + 10 на проміжку:
1) [–5; –3]; 2) [–1; 0]; 3) [–11; –10].
11.25.• При яких значеннях p і q графік функції y = x2 + px + q проходить через точки M (–1; 4) і K (2; 10)?
11.26.• При яких значеннях a і b нулями функції y = ax2 + bx + 7 є числа –2 і 3?
11.27.• При яких значеннях a і b парабола y = ax2 + bx – 4 проходить через точки C (–3; 8) і D (1; 4)?
11.28.• Нехай D — дискримінант квадратного тричлена ax2 + + bx + c. Зобразіть схематично графік квадратичної функції y = ax2 + bx + c, якщо:
1) a > 0, D > 0, c > 0, − b > 0;
2a
2) a > 0, D = 0, − b < 0;
2a
3) ![]() a < 0, D < 0, − b > 0; 2a
a < 0, D < 0, − b > 0; 2a
4) a < 0, c = 0, − b < 0.
2a
11.29.• Нехай D — дискримінант квадратного тричлена ax2 + + bx + c. Зобразіть схематично графік квадратичної функції y = ax2 + bx + c, якщо:
1) a > 0, D < 0, − ![]() b < 0; 3) a < 0, D = 0, −
b < 0; 3) a < 0, D = 0, − ![]() b < 0.
b < 0.
2a 2a
2) a < 0, D > 0, c < 0, − ![]() b > 0;
b > 0;
2a
11.30.• При якому значенні b проміжок (–×; 2] є проміжком зростання функції y = –4x2 – bx + 5?
11.31.• При якому значенні b проміжок (–×; –3] є проміжком спадання функції y = 3x2 + bx – 8?
11.32.• При якому значенні a функція y ax= 2 + (a − 2) x + ![]() є ква-
є ква-
дратичною та її графік має з віссю абсцис одну спільну точку?
11.33.•• При яких значеннях a функція y = 0,5x2 – 3x + a набуває невід’ємних значень при всіх дійсних значеннях x?
11.34.•• При яких значеннях a функція y = –4x2 – 16x + a набуває від’ємних значень при всіх дійсних значеннях x?
11.35.•• При якому значенні c найбільше значення функції y = = –5x2 + 10x + c дорівнює –3?
11.36.•• При якому значенні c найменше значення функції y = = 0,6x2 – 6x + c дорівнює –1?
11.37.•• На рисунку 11.5 зображено графік квадратичної функції y = ax2 + bx + c. Визначте знаки коефіцієнтів a, b і c.
Рис. 11.5 Рис. 11.6
11.38.•• На рисунку 11.6 зображено графік квадратичної функції y = ax2 + bx + c. Визначте знаки коефіцієнтів a, b і c.
11.39.•• При яких значеннях p і q вершиною параболи y = x2 + px + q є точка A (2; 5)?
11.40.•• Парабола y = ax2 + bx + c має вершину в точці C (4; –10) і проходить через точку D (1; –1). Знайдіть значення коефіцієнтів a, b і c.
11.41.•• Знайдіть ординату вершини параболи, фрагмент якої зображено на рисунку 11.7.
Квадратична фунКція
а б
Рис. 11.7
11.42.•• Знайдіть ординату вершини параболи, фрагмент якої зображено на рисунку 11.8.
Рис. 11.8 Рис. 11.9
11.43.•• Сума двох чисел дорівнює 10. Знайдіть:
1) якого найбільшого значення може набувати добуток цих чисел;
2) якого найменшого значення може набувати сума квадратів цих чисел.
11.44.•• Із пункту B у пункт A, відстань між якими дорівнює 13 км, вирушив турист зі швидкістю 6 км/год. Одночасно з ним із пункту A в перпендикулярному напрямку (рис. 11.9) вирушив зі швидкістю 4 км/год другий турист. Через який час після початку руху відстань між туристами буде найменшою?
11.45.•• Ділянку землі прямокутної форми треба обгородити парканом завдовжки 160 м. Яку найбільшу площу може мати ця ділянка?
11.46.•• Побудуйте графік функції:
1) y = 8x+ 2x2 −x3 ; 3) y = xx42−−164 ;
![]()
![]() x4 + 4x2 − 5
x4 + 4x2 − 5
2) y =4) y = x2 − 1 .
11.47.•• Побудуйте графік функції:
1) ![]() y = (x++33)3 ; 3) y = 1
y = (x++33)3 ; 3) y = 1![]() x4−−x12 .
x4−−x12 .
x
x3 − 6x2 + 8x
2) y =;
x
11.48.•• Побудуйте графік функції:
1) y = x | x |; 3) y = x2 – 4 | x | + 3;
2) ![]()
![]() y =(x2 − x − 6); 4) y x= 2 + 3xæ x− 3 − 4. x− 3
y =(x2 − x − 6); 4) y x= 2 + 3xæ x− 3 − 4. x− 3
11.49.•• Побудуйте графік функції:
x3 2
1) y =+ 4x; 2) y = 6 | x | – x .
![]()
11.50.•• Побудуйте графік функції y = x2 + 2x – 3. Користуючись побудованим графіком, установіть, при яких значеннях a рівняння x2 + 2x – 3 = a:
1) має два корені; 2) має один корінь; 3) не має коренів.
11. 51.•• Побудуйте графік функції y = –x2 – 4x + 5. Користуючись побудованим графіком, установіть, скільки коренів має рівняння –x2 – 4x + 5 = a залежно від значення a.
11.52.* Нехай x1 і x2 — нулі функції y = –3x2 – (3a – 2) x + 2a + 3. При яких значеннях a виконується нерівність x1 < –2 < x2?
11.53.* Відомо, що x1 і x2 — нулі функції y = 2x2 – (3a – 1) x + a – 4, x1 < x2. При яких значеннях a число 1 належить проміжку
[x1; x2]?
![]()
11.54. Розв’яжіть рівняння:
1) x4 – 13x2 + 36 = 0; 3) x4 + 9x2 + 8 = 0; 2) x4 – 5x2 – 6 = 0; 4) x4 – 16x2 = 0.
11.55. Знайдіть суму та добуток коренів рівняння:
1) x2 – 5x – 10 = 0; 2) 2x2 + 6x – 7 = 0;
3) −![]() x2 + 8x − 1 = 0.
x2 + 8x − 1 = 0.
11.56. Виконайте дії:
1) ![]() b+ 3 + b− 2; 3) x − x+ 1 . b− 3 b+ 2 2x+ 3 2x− 3 p+ 4 p− 20
b+ 3 + b− 2; 3) x − x+ 1 . b− 3 b+ 2 2x+ 3 2x− 3 p+ 4 p− 20
2) − ; p− 1 p+ 5
11.57. Спростіть вираз:
1) (2 a + 3 b)(4a − 6 ab + 9b) − 9 9b3 ;
2) ![]() (3 2 − 2 28 + 4 63 )æ 7 − 126; 3) (2 − 3 + 6 )(2 + 3 − 6 ).
(3 2 − 2 28 + 4 63 )æ 7 − 126; 3) (2 − 3 + 6 )(2 + 3 − 6 ).
11.58. Моторний човен вирушив по річці від однієї пристані до другої і повернувся назад через 2,5 год, витративши на стоянку 25 хв. Знайдіть швидкість течії річки, якщо власна швидкість човна дорівнює 20 км/год, а відстань між пристанями — 20 км.
11.59. Через одну з двох труб можна наповнити бак водою на 10 хв швидше, ніж через другу. Якщо одночасно відкрити обидві труби, то за 8 хв буде заповнено ![]() бака. За який час можна заповнити цей бак через кожну з труб?
бака. За який час можна заповнити цей бак через кожну з труб?
 УЧиМоСЯ Робити неСтандаРтні кРоки
УЧиМоСЯ Робити неСтандаРтні кРоки
11.60. На дошці записано число 1001. Двоє грають у таку гру. За один хід гравець стирає записане на дошці число, а замість нього записує різницю цього числа й будь-якого його дільника. Гравці роблять ходи по черзі. Програє той, після ходу якого на дошці буде записано число 0. Хто з гравців може забезпечити собі виграш?
 Про деякі перетворення графіків функцій
Про деякі перетворення графіків функцій
Як побудувати графік функції y = f (–x), якщо відомо графік функції y = f (x)
Зазначимо, що коли точка (x0; y0) належить графіку функції y = f (x), то точка (–x0; y0) належить графіку функції y = f (–x).
Справді, f (–(–x0)) = f (x0) = y0.
Тому всі точки графіка функції y = f (–x) можна отримати, замінивши кожну точку графіка функції y = f (x) на точку з такою самою ординатою та протилежною абсцисою.[4]
На рисунку 11.10 показано, як за допомогою графіка функції
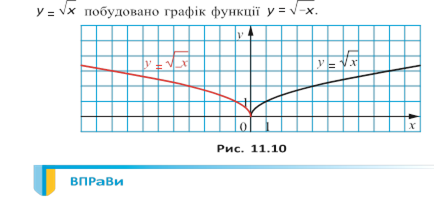
1. Використовуючи графік функції y = f (x), зображений на рисунку 11.11, побудуйте графік функції y = f (–x).
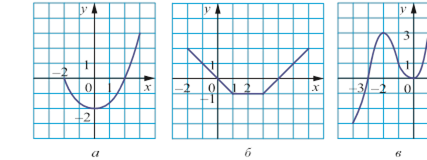
Рис. 11.11
2. ![]() Побудуйте графік функції y = x − 2. Використовуючи отриманий графік, побудуйте графік функції y = −x − 2.
Побудуйте графік функції y = x − 2. Використовуючи отриманий графік, побудуйте графік функції y = −x − 2.
Як побудувати графік функції y = f (| x |), якщо відомо графік функції y = f (x)
Скориставшись означенням модуля, запишемо:
![]() f x( ), якщо xl 0, y f x= () = f x(− ), якщо x < 0.
f x( ), якщо xl 0, y f x= () = f x(− ), якщо x < 0.
Звідси робимо висновок, що графік функції y = f (| x |) при x l 0 збігається з графіком функції y = f (x), а при x < 0 — з графіком функції y = f (–x).
Тоді побудову графіка функції y = f (| x |) можна проводити за такою схемою:
1) побудувати ту частину графіка функції y = f (x), усі точки якої мають невід’ємні абсциси;
2) побудувати ту частину графіка функції y = f (–x), усі точки якої мають від’ємні абсциси.
Об’єднання цих двох частин і складатиме графік функції y = f (| x |).
На рисунку 11.12 показано, як за допомогою графіка функції y = (x – 2)2 побудовано графік функції y = (| x | – 2)2.
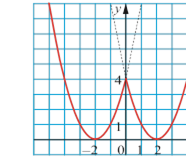
Рис. 11.12
![]()
1. Використовуючи графік функції y = f (x), зображений на рисунку 11.11, побудуйте графік функції y = f (| x |).
2. Використовуючи графік функції y = x + 2, побудуйте графік функції y = | x | + 2.
3. Побудуйте графік функції:
1) ![]() y = | x | – 3; 5) y = ;
y = | x | – 3; 5) y = ;
2) y = x2 – 4 | x |; 6) y =
3) y = x2 + 2 | x | – 3; 7) y = ;
4) y = 2 | x | – x2; 8) y =
Як побудувати графік функції y = | f (x) |, якщо відомо графік функції y = f (x)
Для функції y = | f (x) | можна записати:
![]() f x( ), якщо f x( ) l 0, y = f x( ) = −f x( ), якщо f x( ) < 0.
f x( ), якщо f x( ) l 0, y = f x( ) = −f x( ), якщо f x( ) < 0.
Звідси випливає, що графік функції y = | f (x) | при всіх x, для яких f (x) l 0, збігається з графіком функції y = f (x), а при всіх x, для яких f (x) < 0, — з графіком функції y = –f (x).
Тоді побудову графіка функції y = | f (x) | можна проводити за такою схемою:
1) усі точки графіка функції y = f (x) з невід’ємними ординатами залишити незмінними;
2) точки з від’ємними ординатами замінити на точки з тими самими абсцисами, але протилежними ординатами.
На рисунку 11.13 показано, як за допомогою графіка функції y = x2 – x – 2 побудовано графік функції y = | x2 – x – 2 |.
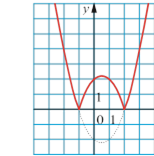
Рис. 11.13
![]()
![]() Приклад 1 Побудуйте графік функції y = x + 1 − 2 .
Приклад 1 Побудуйте графік функції y = x + 1 − 2 .
Розв’язання. Побудову шуканого графіка можна провести за такою схемою:
|
y = |
|
|
|
|
(рис. 11.14). ◄
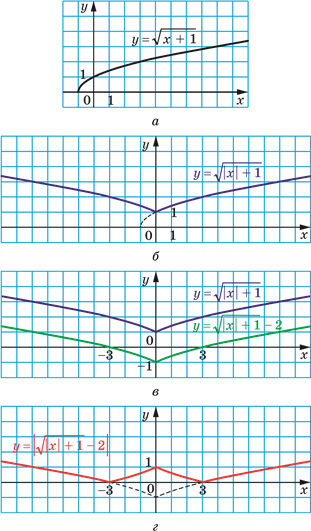
Рис. 11.14
![]()
![]() Приклад 2 Побудуйте графік функції y = | x + 1 | − 1 .
Приклад 2 Побудуйте графік функції y = | x + 1 | − 1 .
Розв’язання. Побудову шуканого графіка можна провести за такою схемою:
![]()
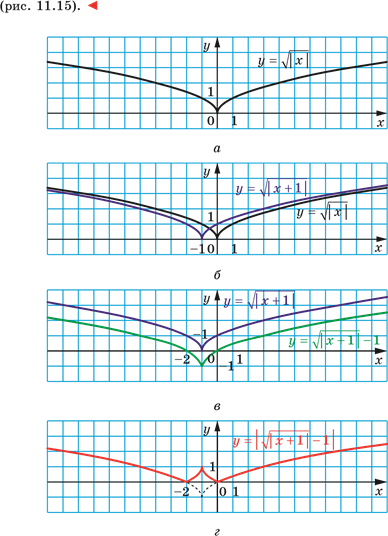
Рис. 11.15
![]()
1. Використовуючи графік функції y = f (x), зображений на рисунку 11.11, побудуйте графік функції:
1) y = | f (x) |; 2) y = | f (| x |) |.
2. Використовуючи графік функції y = x + 2, побудуйте графік функції y = | x + 2 |.
3. Побудуйте графік функції:
1) y = | x – 3 |; 4) y = | 2x – x2 |;
2) y = | x2 – 4x |; 5) y =
3) ![]() y = | x2 + 2x – 3 |; 6) y =.
y = | x2 + 2x – 3 |; 6) y =.
|
4. Побудуйте графік функції: |
|
|
1) y = | | x | – 3 |; |
4) y = | 2 | x | – x2 |; |
2) ![]()
![]() y = | x2 – 4 | x | |; 5) y =
y = | x2 – 4 | x | |; 5) y =
3) y = | x2 + 2 | x | – 3 |; 6) y =
5. Побудуйте графік функції:
1) y =4) y =
2) y = 3 − 5) y = 3 −
3) y =; 6) y =.
Завдання № 2 «Перевірте себе» в тестовій формі
ЗаВданнЯ № 2 «ПеРеВіРте Себе» В теСтоВій фоРМі
1. Чому дорівнює значення функції f (x) = 2x2 – 1 у точці x0 = –3?
А) –19; В) 11;
Б) –13; Г) 17.
2. Серед наведених функцій укажіть квадратичну.
А) y = 2x – 5; В) y = 2x2 – 5;
![]() Б) y = 2 x − 5; Г) y =
Б) y = 2 x − 5; Г) y = ![]() 22 − 5. x
22 − 5. x
3. Областю визначення якої з функцій є проміжок (–×; 6)?
А) y =В) y = 1 ;
6 +x
![]()
![]() Б) y = ; Г) y = 6 − x.
Б) y = ; Г) y = 6 − x.
7
4. Як потрібно паралельно перенести графік функції y = ![]() , щоб x
, щоб x
отримати графік функції y = ![]() 7 ?
7 ?
x− 5
А) На 5 одиниць угору вздовж осі ординат;
Б) на 5 одиниць уліво вздовж осі абсцис;
В) на 5 одиниць управо вздовж осі абсцис;
Г) на 5 одиниць униз уздовж осі ординат.
5. ![]() Графік функції y = x паралельно перенесли на 2 одиниці вліво та на 7 одиниць униз. Графік якої функції було отримано?
Графік функції y = x паралельно перенесли на 2 одиниці вліво та на 7 одиниць униз. Графік якої функції було отримано?
Квадратична фунКція
7. ![]() Графік якої функції зображено на рисунку?
Графік якої функції зображено на рисунку?
А) y = x2 – 1; Б) y = x2 + 1;
В) y = (x – 1)2;
Г) y = (x + 1)2.
8. Укажіть координати вершини параболи y = 3 (x – 4)2 – 5.
А) (4; 5); В) (4; –5); Б) (–4; 5); Г) (–4; –5).
9. ![]() На рисунку зображено графік функції y = f (x), визначеної на множині дійсних чисел. Користуючись рисунком, укажіть проміжок спадання функції.
На рисунку зображено графік функції y = f (x), визначеної на множині дійсних чисел. Користуючись рисунком, укажіть проміжок спадання функції.
А) [–4; 1]; В) [–2; 3];
Б) [–3; 3]; Г) [–3; 1].
10. Знайдіть абсцису вершини параболи y = 2x2 – 12x + 3.
А) 6; В) 3;
Б) –6; Г) –3.
11. Вершина якої з парабол належить осі абсцис?
![]() А) y = x2 – 6; В) y = (x – 6)2; Б) y = x2 – 6x; Г) y = (x – 6)2 + 2.
А) y = x2 – 6; В) y = (x – 6)2; Б) y = x2 – 6x; Г) y = (x – 6)2 + 2.
12. На рисунку зображено графік функції y = –x2 + 2x + 4. Користую чись рисунком, знайдіть область значень функції.
А) (–×; +×);
Б) (–×; 1];
В) [1; +×); Г) (–×; 5].
13. На рисунку зображено графік функції y = x2 + 4x + 1. Користуючись рисунком, укажіть проміжок зростання функції.
А) (–×; –2];
Б) [–2; +×);
В) [–3; +×);
Г) визначити неможливо.
14. Знайдіть нулі функції y = 2x2 + x – 6. А) –1,5; –2; В) –1,5; 2;
Б) 1,5; 2; Г) 1,5; –2.
Завдання № 2 «Перевірте себе» в тестовій формі
15. При яких значеннях b і c вершина параболи y = x2 + bx + c знаходиться в точці M (3; 8)?
А) b = 6, c = –19;
Б) b = –6, c = 17;
![]() В) b = –3, c = 8; Г) визначити неможливо.
В) b = –3, c = 8; Г) визначити неможливо.
16. На рисунку зображено графік квадратичної функції y = ax2 + bx + c. Укажіть правильне твердження, якщо D — дискримінант квадратного тричлена ax2 + bx + c.
А) b > 0, D > 0; В) b < 0, D < 0; Б) b > 0, D < 0; Г) b > 0, D = 0.
17. При якому значенні a найменше значення функції y = 3x2 – 6x + a дорівнює 4?
А) –5; Б) 4; В) 7; Г) 8.
18. Відомо, що m – n = 8. Знайдіть множину значень виразу mn.
А) [–16; +×);
Б) [8; +×);
В) (–×; +×);
Г) визначити неможливо.
 12. Розв’язування квадратних нерівностей
12. Розв’язування квадратних нерівностей
На рисунку 12.1 зображено графік деякої функції y = f (x), областю визначення якої є множина дійсних чисел.
![]() За допомогою цього графіка легко визначити проміжки знакосталості функції f, а саме: y > 0 на кожному з проміжків (–5; –2) і (1; +×); y < 0 на кожному з проміжків (–×; –5) і (–2; 1).
За допомогою цього графіка легко визначити проміжки знакосталості функції f, а саме: y > 0 на кожному з проміжків (–5; –2) і (1; +×); y < 0 на кожному з проміжків (–×; –5) і (–2; 1).
Знайшовши проміжки знакосталос-
Рис. 12.1 ті функції f, ми тим самим розв’язали нерівності f (x) > 0 і f (x) < 0.
Проміжки (–5; –2) і (1; +×) разом
складають множину розв’язків нерівності f (x) > 0. У таких ви падках говорять, що множина розв’язків нерівності f (x) > 0 є об’єднанням зазначених проміжків. Об’єднання проміжків записують за допомогою спеціального символу Ÿ.
Тоді множину розв’язків нерівності f (x) > 0 можна записати так: (−5; −2) Ÿ (1; +×).
Множину розв’язків нерівності f (x) < 0 можна записати так: (−×; −5) Ÿ (−2; 1).
Такий метод розв’язування нерівностей f (x) > 0 і f (x) < 0 за допомогою графіка функції y = f (x) називають графічним.
Покажемо, як за допомогою цього методу розв’язують квадратні нерівності.
Означення. Нерівності виду ax2 + bx + c > 0, ax2 + bx + c < 0, ax bx c2 + + l 0, ax bx c2 + + m0, де x — змінна, a, b і c — деякі чис
ла, причому a ≠ 0, називають квадратними.
З’ясуємо, як визначити положення графіка квадратичної функції y = ax2 + bx + c відносно осі абсцис.
Наявність і кількість нулів квадратичної функції y = ax2 + bx + c визначають за допомогою дискримінанта D квадратного тричлена ax2 + bx + c: якщо D > 0, то нулів у функції два; якщо D = 0, то нуль один; якщо D < 0, то нулів немає.
Знак старшого коефіцієнта квадратного тричлена ax2 + bx + c визначає напрям віток параболи y = ax2 + bx + c. При a > 0 вітки напрямлені вгору, при a < 0 — униз.
Схематичне розміщення параболи y = ax2 + bx + c відносно осі абсцис залежно від знаків чисел a і D відображено в таблиці (x1 і x2 — нулі функції, x0 — абсциса вершини параболи).
|
|
D > 0 |
D = 0 |
D < 0 |
|
a > 0 |
|
|
|
|
a < 0 |
|
|
|
Пояснимо, як використовувати цю таблицю для розв’язування квадратних нерівностей.
![]() Нехай, наприклад, потрібно розв’язати нерівність ax2 + bx + c > 0, де a < 0 і D > 0. Цим умовам відповідає клітинка 4 таблиці. Тоді зрозуміло, що відповіддю буде проміжок (x1; x2), на якому графік відповідної квадратичної функції розміщено над віссю абсцис.
Нехай, наприклад, потрібно розв’язати нерівність ax2 + bx + c > 0, де a < 0 і D > 0. Цим умовам відповідає клітинка 4 таблиці. Тоді зрозуміло, що відповіддю буде проміжок (x1; x2), на якому графік відповідної квадратичної функції розміщено над віссю абсцис.
![]() Приклад 1 Розв’яжіть нерівність 2x2 – x – 1 > 0.
Приклад 1 Розв’яжіть нерівність 2x2 – x – 1 > 0.
Розв’язання. Для квадратного тричлена 2x2 – x – 1 маємо:
![]() a = 2 > 0, D = 9 > 0. Цим умовам відповідає клітинка 1 таблиці.
a = 2 > 0, D = 9 > 0. Цим умовам відповідає клітинка 1 таблиці.
Розв’яжемо рівняння 2x2 – x – 1 = 0. Отримаємо x1 = −![]() , x2 = 1.
, x2 = 1.
Тоді схематично графік функції y = 2x2 – x – 1 можна зобразити так, як показано на рисунку 12.2.
![]() Із рисунка 12.2 видно, що відповідна квадратична функція набуває додатних значень на кожному з проміжків −×; −
Із рисунка 12.2 видно, що відповідна квадратична функція набуває додатних значень на кожному з проміжків −×; − ![]() 1 і (1; +×).
1 і (1; +×).
2
![]() −×; − 1 ∪ (1; +×). ◄ Рис. 12.2
−×; − 1 ∪ (1; +×). ◄ Рис. 12.2
Відповідь:
2
![]() Приклад 2 Розв’яжіть нерівність –9x2 + 6x – 1 < 0.
Приклад 2 Розв’яжіть нерівність –9x2 + 6x – 1 < 0.
Розв’язання. Маємо: a = –9, D = 0. Цим умовам відповідає 1
![]() клітинка 5 таблиці. Установлюємо, що x0 =
клітинка 5 таблиці. Установлюємо, що x0 = ![]() . Тоді схематично
. Тоді схематично
3
графік функції y = –9x2 + 6x – 1 можна зобразити так, як показано на рисунку 12.3.
![]() Із рисунка 12.3 видно, що розв’язками нерівності є всі числа, крім
Із рисунка 12.3 видно, що розв’язками нерівності є всі числа, крім ![]() .
.
Зауважимо, що цю нерівність можна розв’язати іншим способом. Перепишемо дану Рис. 12.3 нерівність так: 9x2 – 6x + 1 > 0.
Тоді (3x – 1)2 > 0.
Звідси отримуємо той самий результат.
![]() Відповідь: −×; 1 ∪ 1; +×. ◄
Відповідь: −×; 1 ∪ 1; +×. ◄
3 3
Приклад 3 Розв’яжіть нерівність 3x2 – x + 1 < 0.
![]() Розв’язання. Маємо: a = 3 > 0, D = –11 < 0. Цим умовам відповідає клітинка 3 таблиці. У цьому випадку графік функції
Розв’язання. Маємо: a = 3 > 0, D = –11 < 0. Цим умовам відповідає клітинка 3 таблиці. У цьому випадку графік функції
y = 3x2 – x + 1 не має точок з від’ємними ординатами. Відповідь: розв’язків немає. ◄
![]() Приклад 4 Розв’яжіть нерівність 0 2, x2 + 2x + 5 m 0.
Приклад 4 Розв’яжіть нерівність 0 2, x2 + 2x + 5 m 0.
![]() Розв’язання. Оскільки a = 0,2, D = 0, то даному випадку відповідає клітинка 2 таблиці, причому x0 = –5. Але в цьому випадку квадратична функція набуває тільки невід’ємних значень. Отже, дана нерівність має єдиний розв’язок x = –5. Відповідь: –5. ◄
Розв’язання. Оскільки a = 0,2, D = 0, то даному випадку відповідає клітинка 2 таблиці, причому x0 = –5. Але в цьому випадку квадратична функція набуває тільки невід’ємних значень. Отже, дана нерівність має єдиний розв’язок x = –5. Відповідь: –5. ◄
1. За допомогою якого символу записують об’єднання проміжків?
2. Які нерівності називають квадратними?
3. ![]() Які можливі випадки розміщення параболи y = ax2 + bx + cвідносно осі абсцис залежно від знаків a і D, де D — дискримінант квадратного тричлена ax2 + bx + c? Зобразіть схематично ці випадки.
Які можливі випадки розміщення параболи y = ax2 + bx + cвідносно осі абсцис залежно від знаків a і D, де D — дискримінант квадратного тричлена ax2 + bx + c? Зобразіть схематично ці випадки.
![]()
12.1.° Які із чисел –2; 0; 1 є розв’язками нерівності:
1) x2 – x – 2 < 0; 2) x2 + xl 0; 3) –3x2 – x + 2 > 0?
![]() 12.2.° На рисунку 12.4 зображено графік функції y = x2 + 4x – 5. Знайдіть множину розв’язків нерівності:
12.2.° На рисунку 12.4 зображено графік функції y = x2 + 4x – 5. Знайдіть множину розв’язків нерівності:
1) x2 + 4x – 5 < 0; 3) x2 + 4x – 5 > 0;
2) x2 + 4x − 5 m 0; 4) x2 + 4x − 5 l 0.
12.3.° На рисунку 12.5 зображено графік функції y = –3x2 – 6x. Знайдіть множину розв’язків нерівності:
1) –3x2 – 6x < 0; 3) –3x2 – 6x > 0; Рис. 12.4
12.4.° На рисунку 12.6 зображено графік функції y = x2 – 4x + 4.
Знайдіть множину розв’язків нерівності: 1) x2 – 4x + 4 < 0; 3) x2 – 4x + 4 > 0;
2) x2 − 4x + 4 m 0; 4) x2 − 4x + 4 l 0.
12.5.° На рисунку 12.7 зображено графік функції y = –x2 + 2x – 2. Знайдіть множину розв’язків нерівності: 1) –x2 + 2x – 2 < 0; 3) –x2 + 2x – 2 > 0;
2) −x2 + 2x − 2 m 0; 4) −x2 + 2x − 2 l 0.
12.6.° Розв’яжіть нерівність:
1) x2 + 6x – 7 < 0; 5) 3x2 − 7x + 4 m 0;
2) x2 − 2x − 48 l 0; 6) 2x2 + 3x + 1 > 0;
3) –x2 – 6x – 5 > 0; 7) 4x2 − 12xm 0;
4) –x2 + 4x – 3 < 0; 8) 4x2 – 9 > 0;
|
9) x2 – 12x + 36 > 0; |
13) 2x2 – x + 3 > 0; |
|
10) 4x2 − 12x + 9 l 0; |
14) 3x2 − 4x + 5 m 0; |
|
11) x2 + 4x + 4 < 0; |
15) –4x2 + 5x – 7 > 0; |
|
12) 49x2 − 14x + 1 m 0; 12.7.° Розв’яжіть нерівність: |
16) −2x2 + 3x − 2 m 0. |
|
1) x2 + 4x + 3 > 0; |
7) 5x2 − 3x + 1l 0; |
|
2) x2 − 3x + 2 m 0; |
8) –3x2 + 6x – 4 > 0; |
3) –x2 + 12x + 45 < 0; 9) ![]() x2 − 2x + 3 m 0;
x2 − 2x + 3 m 0;
4) −3x2 − 5x− 2 l 0; 10) −x2 + ![]() x −
x − ![]() > 0;
> 0;
5) x2 – 5x > 0; 11) 2x2 – 2x + 0,5 < 0.
6) −25x2 + 16 m 0;
12.8.° Знайдіть множину розв’язків нерівності:
1) x2 m 49; 2) x2 > 5; 3) 7x2 m 4x; 4) 0,9x2 < –27x.
12.9.° Знайдіть множину розв’язків нерівності:
1) x2 > 1; 2) x2 < 3; 3) −3x2 l − 12x; 4) –2x2 < –128.
12.10.• Розв’яжіть нерівність:
1) x (x + 5) – 2 < 4x;
2) 11 − (x + 1)2 mx;
3) (2x + 1)2 − (x + 1) (x − 7) m5;
4) 5x (x + 4) – (2x – 3) (2x + 3) > 30;
5) (3x – 7) (x + 2) – (x – 4) (x + 5) > 30;
![]() 2x2 − 1 3 − 4x 8x− 5
2x2 − 1 3 − 4x 8x− 5
6) ![]() − + m.
− + m.
4 6 8
12.11.• Розв’яжіть нерівність: 1) 2 (x2 + 2) lx x( + 5);
2) x – (x + 4) (x + 5) > –5;
3) (6x – 1) (6x + 1) – (12x – 5) (x + 2) < 7 – 3x; x− 1 2x− 3 x2 + 3x
4) ![]() − < .
− < .
4 2 8
12.12.• При яких значеннях x:
1) значення тричлена –3x2 + 6x + 1 більші за −![]() ;
;
2) значення тричлена –5x2 + 11x + 2 не більші за −![]() ?
?
12.13.• При яких значеннях x:
1) значення тричлена x2 – 2x – 11 менші від ![]() ;
;
2) значення тричлена –3x2 + 8x + 6 не менші від −![]() ?
?
12.14.• При яких значеннях аргументу значення функції
y = −![]() x2 +
x2 + ![]() x + 9
x + 9
більші за відповідні значення функції y = 2x – 1? 12.15.• При яких значеннях аргументу значення функції y = ![]() x2 − 7x + 1
x2 − 7x + 1
менші від відповідних значень функції y = −![]() x2 − 4?
x2 − 4?
12.16.• Знайдіть цілі розв’язки нерівності:
1) x2 + 5xm 0; 3) 6x2 + x − 2 m 0;
2) x2 – 10 < 0; 4) −![]() x2 + x + 3 > 0.
x2 + x + 3 > 0.
12.17.• Скільки цілих розв’язків має нерівність:
1) 20 – 8x – x2 > 0; 2) 4x2 – 15x – 4 < 0?
12.18.• Знайдіть найменший цілий розв’язок нерівності: 1) 42 – x2 – x > 0; 2) 2x2 – 3x – 20 < 0.
12.19.• Знайдіть найбільший цілий розв’язок нерівності: 1) 1,5x2 – 2x – 2 < 0; 2) −2x2 − 15x − 25 l 0.
12.20.• Складіть яку-небудь квадратну нерівність, множина розв’язків якої:
1) є об’єднанням проміжків (–×; –4) і (8; +×);
2) є проміжком [–2; 9];
3) складається з одного числа 7.
12.21.• Знайдіть область визначення функції:
1) y = −x2 + 3x + 4; 3) y = 1 ;
x2 + 4x− 12
2) ![]()
![]() y = 2x2 + 5x − 3; 4) y = x+ 2 .
y = 2x2 + 5x − 3; 4) y = x+ 2 .
6x− 2x2
12.22.• Знайдіть область визначення виразу:
![]() 1) 2x2 − 9x − 18; 2)
1) 2x2 − 9x − 18; 2) ![]() .
.
12.23.• Чи рівносильні нерівності:
1) x2 – 2x – 15 > 0 і x2 − 2x − 15 l 0;
2) ![]() x2 − −x1 20 < 0 і
x2 − −x1 20 < 0 і ![]() x2 − x1 − 20 m 0;
x2 − x1 − 20 m 0;
3) x2 – 6x + 10 > 0 і −x2 + x − 1 m 0; 4) x2 + 2x + 3 < 0 і –2x2 – 4 > 0?
12.24.• При яких значеннях a не має коренів рівняння:
1) x2 – ax + 4 = 0; 3) 4,5x2 – (4a + 3) x + 3a = 0?
2) x2 + (a – 2) x + 25 = 0;
12.25.• При яких значеннях b має два різних корені рівняння:
1) x2 – 8bx + 15b + 1 = 0; 2) 2x2 + 2 (b – 6) x + b – 2 = 0?
12.26.•• Розв’яжіть систему нерівностей:
x2 − x − 6 m 0, x2 − 9x − 10 m 0,
1) x > 0; 3) 6x x− 2 < 0;
2x2 − 11x − 6 l 0, x2 − x − 12 l 0, 2) x + 4 l 0; 4) x2 + 3x − 10 < 0.
12.27.•• Розв’яжіть систему нерівностей:
−6x2 + 13x − 5 m 0, x2 − 7x − 18 < 0, 1) 6 − 2x > 0; 2) 5x x− 2 m 0.
12.28.•• Знайдіть цілі розв’язки системи нерівностей:
![]()
![]() −2x2 − 5x + 18 l 0, x2 − ( 5 − 3)x − 3 5 m 0, 1) x2 + 4x − 5 m 0; 2) x2 + x > 0.
−2x2 − 5x + 18 l 0, x2 − ( 5 − 3)x − 3 5 m 0, 1) x2 + 4x − 5 m 0; 2) x2 + x > 0.
12.29.•• Знайдіть область визначення функції:
1) ![]()
![]() y = x2 − 54x− 12 + x + 1; 3) y = x2 − 5x − 14 − x2 9− 81;
y = x2 − 54x− 12 + x + 1; 3) y = x2 − 5x − 14 − x2 9− 81;
2) y = x− 3 + 8 ; 4) y = 1 + 2 .
18 + 3x x− 2 x− 5 6 − 7x− 3x2 x+ 1
12.30.•• Знайдіть область визначення функції:
1) y = 20 + 4x − 3x2 + 3 ; 2) y = x+ 5 + x− 1 .
8 − 4x 35 + 2x x− 2 | x | − 6
12.31.•• Знайдіть множину розв’язків нерівності:
1) x2 – 8 | x | – 33 < 0; 2) 8x2 + 7 x − 1l 0.
12.32.•• Знайдіть множину розв’язків нерівності:
![]() 1) 5x2 − 7 x + 2 l 0; 2) x2 + 10 x − 24 m 0;
1) 5x2 − 7 x + 2 l 0; 2) x2 + 10 x − 24 m 0;
12. 33.•• Розв’яжіть нерівність:
1) x æ(x2 + 3x − 10) < 0; 4) (x + 5)2 (x2 – 2x – 15) > 0;
2) ![]() x x( 2 + 2x − 8) m 0; 5) x2 +−7x4)−2 8 l 0;
x x( 2 + 2x − 8) m 0; 5) x2 +−7x4)−2 8 l 0;
(x
![]() 2 2 x2 + 10x− 11
2 2 x2 + 10x− 11
3) (x – 2) (x – 8x – 9) < 0; 6) m 0.
|
12.34.•• Розв’яжіть нерівність: |
(x+ 3)2 |
1) x æ(x2 − 5x + 6) > 0; 3) (x + 3)2 (x2 – x – 6) > 0;
2
2) ![]() x x( 2 + 6x − 40) > 0; 4) 3x − 8x2− 3 m 0.
x x( 2 + 6x − 40) > 0; 4) 3x − 8x2− 3 m 0.
(x − 1)
12.35.* Розв’яжіть нерівність:
![]()
![]() 1) (x + 4) x2 − 2x − 15 > 0; 3) (x + 4) x2 − 2x − 15 < 0; 2) (x + 4) x2 − 2x − 15 l 0; 4) (x + 4) x2 − 2x − 15 m 0.
1) (x + 4) x2 − 2x − 15 > 0; 3) (x + 4) x2 − 2x − 15 < 0; 2) (x + 4) x2 − 2x − 15 l 0; 4) (x + 4) x2 − 2x − 15 m 0.
12.36.* Розв’яжіть нерівність:
1) (x − 3) 14 + 5x x− 2 > 0; 3) (x − 3) 14 + 5x x− 2 < 0; 2) (x − 3) 14 + 5x x− 2 l 0; 4) (x − 3) 14 + 5x x− 2 m 0.
12.37.* При яких значеннях a дана нерівність виконується при всіх дійсних значеннях x:
1) x2 – 4x + a > 0;
2) x2 + (a − 1) x + 1 − a a− 2 l 0;
3) −![]() x2 + 5ax − 9a2 − 8a < 0;
x2 + 5ax − 9a2 − 8a < 0;
4) (a – 1) x2 – (a + 1) x + a + 1 > 0?
12.38.* При яких значеннях a не має розв’язків нерівність: 1) –x2 + 6x – a > 0;
2) x2 – (a + 1) x + 3a – 5 < 0;
3) ax2 + (a – 1) x + (a – 1) < 0?
12.39.* Для кожного значення a розв’яжіть систему нерівностей:
x2 − 5x + 4 > 0, 4x2 − 3x− 1 m 0,
1) 2)
x a> ; x a< .
12.40.* Для кожного значення a розв’яжіть систему нерівностей:
x2 − x − 72 < 0, x2 − 9x + 8 > 0,
1) 2)
x a> ; x a< .
![]()
12.41. Спростіть вираз:
x2 + 3xy x2 − 9y2 4a2 − 12ab+ 9b2 2a2 − 8ab+ 8b2
![]()
![]() 1) x+ 6 : 2x+ 12 ; 2) 2a2 − 8b2 æ 6a− 9b .
1) x+ 6 : 2x+ 12 ; 2) 2a2 − 8b2 æ 6a− 9b .
12.42. Знайдіть значення виразу, використовуючи властивості арифметичного квадратного кореня:
1) ![]() 20æ æ66 330; 3) 2 18æ3 30æ5 15;
20æ æ66 330; 3) 2 18æ3 30æ5 15;
2) ![]() 35æ123 ; 4) 6 10æ æ45 50.
35æ123 ; 4) 6 10æ æ45 50.
12.43. Перша бригада може зібрати врожай за 12 днів. Другій бригаді для виконання цієї ж роботи потрібно 75 % цього часу. Після того як перша бригада пропрацювала 5 днів, до неї приєдналася друга бригада, і вони разом закінчили роботу. Скільки днів бригади працювали разом?
12.44. ![]() Під час першої поїздки автомобіля витратили 10 % бензину, який був у баку, а під час другої — 25 % решти. Після цього в баку залишилося на 13 л менше бензину, ніж було спочатку. Скільки літрів бензину було в баку до першої поїздки? готУЄМоСЯ до ВиВЧеннЯ ноВоЇ теМи
Під час першої поїздки автомобіля витратили 10 % бензину, який був у баку, а під час другої — 25 % решти. Після цього в баку залишилося на 13 л менше бензину, ніж було спочатку. Скільки літрів бензину було в баку до першої поїздки? готУЄМоСЯ до ВиВЧеннЯ ноВоЇ теМи
12.45. Чи є пара чисел (2; –3) розв’язком рівняння:
1) 4x – 3y = 17; 2) x2 + 5 = y2; 3) xy = 6?
12.46. Графік рівняння 5x – y = 2 проходить через точку A (4; b). Чому дорівнює значення b?
12.47. Побудуйте графік рівняння:
1) 4x + y = 3; 6) x2 + y2 = 4;
2) 2x – 3y = 6; 7) x2 + 2x + y2 – 6y + 10 = 0; 3) xy = –8; 8) (x – 3) (y – x) = 0;
2 2 y x−
4) (x – 2) + y = 0; 9) ![]() y2 − 1 = 0.
y2 − 1 = 0.
5) (x – 2)2 + (y + 1)2 = 9;
12.48. Яка з пар чисел (–2; 1), (2; –1), (6; 4) є розв’язком системи
3x − 8y = −14, рівнянь 4x y+ = 28?
12.49. Розв’яжіть графічно систему рівнянь:
x − 2y = 1, x y+ = −5,
1) y x− = −2; 2) 4x y− = −5.
12.50. Розв’яжіть систему рівнянь:
|
2x y+ = 10, 1) − 7y = 2; 4x |
2x − 9y = 11, 3) + 9y = 25; 7x |
|
4y x− = 11, 2) − 2y = 17; 5x |
3x − 2y = 1, 4) + 7y = −26. 12x |
 13. Системи рівнянь із двома змінними
13. Системи рівнянь із двома змінними
У 7 класі ви ознайомилися з графічним методом розв’язування систем рівнянь. Нагадаємо, що його сутність полягає в пошуку координат спільних точок графіків рівнянь, які входять до системи. На уроках геометрії ви дізналися, що графіком рівняння (x – a)2 + + (y – b)2 = R2, де R > 0, є коло радіуса R із центром (a; b). Ви також навчилися будувати графік квадратичної функції. Усе це розширює можливості застосування графічного методу для розв’язування систем рівнянь.
![]() Приклад 1 Розв’яжіть графічно систему рівнянь
Приклад 1 Розв’яжіть графічно систему рівнянь
x2 − 4x y− + 3 = 0,
![]()
y − x + 1 = 0.
Розв’язання. Перше рівняння системи рівносильне такому: y = x2 – 4x + 3. Його графіком є парабола, зображена на рисунку 13.1.
Графіком другого рівняння є пряма, яка перетинає побудовану параболу у двох точках: (1; 0) і (4; 3) (див. рис. 13.1).
Як відомо, графічний метод не гарантує того, що отриманий результат є точ-
ним. Тому знайдені розв’язки потрібно Рис. 13.1 перевірити. Перевірка підтверджує, що пари чисел (1; 0) і (4; 3) справді є розв’язками даної системи.
Відповідь: (1; 0), (4; 3). ◄
Зауважимо, що ця система є «зручною» для графічного методу: координати точок перетину графіків виявилися цілими числами. Зрозуміло, що така ситуація трапляється далеко не завжди. Тому графічний метод є ефективним тоді, коли потрібно визначити кількість розв’язків або достатньо знайти їх наближено.
Систему, що розглядається, можна розв’язати й не звертаючись до графіків рівнянь. Готуючись до вивчення цієї теми, ви повторили метод підстановки для розв’язування систем лінійних рівнянь. Цей метод є ефективним і для розв’язування більш складних систем, у яких тільки одне рівняння є лінійним, і для деяких систем, у яких узагалі лінійних рівнянь немає.
x2 − 4x y− + 3 = 0, Розв’яжемо систему методом підстановки.
y − x + 1 = 0
Виразимо змінну y через змінну x у другому рівнянні системи: y = x – 1.
Підставимо в перше рівняння замість y вираз x – 1: x2 – 4x – (x – 1) + 3 = 0.
Отримали рівняння з однією змінною. Спростивши його, отримаємо квадратне рівняння x2 – 5x + 4 = 0.
Звідси x1 = 1, x2 = 4.
Значення y, які відповідають отриманим значенням x, знайдемо з рівняння y = x – 1. Маємо:
y1 = 1 – 1 = 0, y2 = 4 – 1 = 3.
Отже, ми ще раз установили, що пари чисел (1; 0) і (4; 3) є розв’язками розглядуваної системи рівнянь.
![]() Приклад 2 Визначте кількість розв’язків системи рівнянь
Приклад 2 Визначте кількість розв’язків системи рівнянь
x2 + y2 = 9,
7
xy = ![]() 2.
2.
Розв’язання. Графіком першого рівняння системи є коло радіуса 3 із центром (0; 0).
3,5
Друге рівняння рівносильне такому: y = ![]() . Графіком цього x
. Графіком цього x
рівняння є гіпербола.
Зобразимо коло та гіперболу на одній координатній площині (рис. 13.2). Бачимо, що графіки перетинаються в чотирьох точках. Отже, дана система має чотири розв’язки. ◄
![]() Рисунок 13.2 також дає змогу знайти наближені значення розв’язків даної системи.
Рисунок 13.2 також дає змогу знайти наближені значення розв’язків даної системи.
Не звертаючись до графічного методу, можна знайти точні значення розв’язків цієї системи.
Готуючись до вивчення цієї теми, ви повторили метод додавання для розв’язування систем лінійних рівнянь. Покажемо, як цей метод «пра-
цює» під час розв’язування більш Рис. 13.2 складних систем.
Помножимо друге рівняння розглядуваної системи на 2. Отри-
x2 + y2 = 9,
маємо:
2xy = 7.
Додамо почленно ліві та праві частини рівнянь. Отримуємо: x2 + y2 + 2xy = 16. Звідси (x + y)2 = 16; x + y = 4 або x + y = –4.
Зрозуміло, що для розв’язування заданої системи досить розв’язати дві простіші системи.
x y+ = 4, y = 4 − x, y = 4 − x,
1) 2xy = 7. Звідси 2x (4 − x) = 7; 2x2 − 8x + 7 = 0.
Розв’язуючи друге рівняння цієї системи, отримуємо: x1 = ![]() , x2 =
, x2 = ![]() .
.
Тоді y1 = ![]() , y2 =
, y2 = ![]() .
.
x y+ = −4, y = −4 − x, y = −4 − x,
2) 2xy = 7. Звідси 2x (−4 − x) = 7; 2x2 + 8x + 7 = 0.
![]()
![]()
![]() Розв’язуючи друге рівняння цієї системи, отримуємо: x3 =
Розв’язуючи друге рівняння цієї системи, отримуємо: x3 = ![]() , x4 =
, x4 = ![]() .
.
Очевидно, що знайти такі розв’язки графічним способом неможливо.
У 8 класі ви ознайомилися з методом заміни змінних для розв’язування рівнянь. Цей метод застосовують і для розв’язування цілої низки систем рівнянь.
![]() x y+ + x y− = 5,
x y+ + x y− = 5,
![]() Приклад 3 Розв’яжіть систему рівнянь − x y+ 2
Приклад 3 Розв’яжіть систему рівнянь − x y+ 2
x y
x2 + y2 = 10.
x y+ x y− 1
![]() Розв’язання. Нехай
Розв’язання. Нехай ![]() = t. Тоді = .
= t. Тоді = .
x y− x y+ t
![]() Тепер перше рівняння системи можна записати так: t + 1 = 5. t 2
Тепер перше рівняння системи можна записати так: t + 1 = 5. t 2
Звідси 2t2 – 5t + 2 = 0; t1 = 2, t2 = ![]() .
.
Для розв’язування заданої системи досить розв’язати дві простіші системи.
![]()
xx yx y2+−+ y=2 2=,10. Звідси x y2++ y=2 2=x10−;2y, 10x =y23y=,10.
1)
x
З другого рівняння отримуємо: y1 = 1, y2 = –1. Тоді x1 = 3, x2 = –3.
![]() xx y2+−+ y=2 12=,10. Звідси 2x2 ++y22y x y==10−; , 10x = −y2 3=y10, .
xx y2+−+ y=2 12=,10. Звідси 2x2 ++y22y x y==10−; , 10x = −y2 3=y10, .
2) x y
x
З другого рівняння отримуємо: y3 = 1, y4 = –1. Тоді x3 = –3, x4 = 3.
Відповідь: (3; 1), (–3; –1), (–3; 1), (3; –1). ◄
2x + 2y xy+ = 8,
![]() Приклад 4 Розв’яжіть систему рівнянь x2 + y2 + 3x + 3y = 14.
Приклад 4 Розв’яжіть систему рівнянь x2 + y2 + 3x + 3y = 14.
Розв’язання. Зауважимо, що дана система не зміниться, якщо замінити x на y, а y на x. У таких випадках може виявитися ефективною заміна x + y = u, xy = v.
Перепишемо дану систему так:
2 (x y+ ) + xy = 8,
(x y+ )2 − 2xy + 3 (x y+ ) = 14.
Виконаємо зазначену заміну. Отримаємо систему:
2u + v = 8,
2
u − 2v + 3u = 14.
Її можна розв’язати методом підстановки (зробіть це самостійно). Отримуємо:
u = 3, u = −10,
v = 2 або v = 28.
Залишається розв’язати дві системи:
x y+ = 3, x y+ = −10,
xy = 2 і xy = 28.
Кожну з них можна розв’язати методом підстановки. Проте тут зручно скористатися теоремою, оберненою до теореми Вієта. Так,
x y+ = 3,
для системи xy = 2 можна вважати, що x і y — корені квадрат
ного рівняння t2 – 3t + 2 = 0. Звідси t1 = 1, t2 = 2. Отже, пари чисел (1; 2) і (2; 1) є розв’язками цієї системи. Використовуючи теорему, обернену до теореми Вієта, легко
x y+ = −10,
переконатися (зробіть це самостійно), що система xy = 28
розв’язків не має.
Відповідь: (1; 2), (2; 1). ◄
1. Які методи розв’язування систем рівнянь ви знаєте?
2. ![]() Поясніть сутність графічного методу розв’язування систем рівнянь.
Поясніть сутність графічного методу розв’язування систем рівнянь.
3. У яких випадках графічний метод є найбільш ефективним?
ВПРаВи
13.1.° Розв’яжіть графічно систему рівнянь:
x y+ = 5, x2 + y2 = 4,
1) xy = 6; 3) x y+ = 2;
y x+ 2 = 3, x2 + y2 = 25,
2) 4)
y x= − 1; xy = −12.
13.2.° Розв’яжіть графічно систему рівнянь:
y x= + 2, y x= 2 − 4, x y+ = 3,
1) xy = 8; 2) 2x y+ = −1; 3) x2 + y2 = 9.
13.3.° Розв’яжіть методом підстановки систему рівнянь:
y x= + 3, y x− = 2, xy = 15,
1) x2 − 2y = 9; 3) x2 − 2xy = 3; 5) 2x y− = 7;
x y+ = 5, x − 4y = 2, x y− = 4,
2) xy = 4; 4) xy + 2y = 8; 6) x2 + y2 = 8.
13.4.° Розв’яжіть методом підстановки систему рівнянь:
x y− = 3, y − 2x2 = 2,
1) xy = 28; 3) 3x y+ = 1;
y2 − x = 14, x2 − 2y2 = 8,
2) 4)
x y− = −2; x y+ = 6.
13.5.• Установіть графічно кількість розв’язків системи рівнянь:
![]() x2 + y2 = 3, y = x, xy = −6,
x2 + y2 = 3, y = x, xy = −6,
1) y x= ; 3) x y− = 2; 5) 2x y− = 3;
x2 + y2 = 4, y x= 2 − 3, x2 − 4x y+ = −1,
2) 2 4) 2 6)
y = 2 − x ; y = 6 − x ; xy = 4.
13.6.• Установіть графічно кількість розв’язків системи рівнянь:
y = (x − 5)2, y x− 2 = 1,
1) 3) 2
|
x2 + y2 = 1, 2) y x− = 3; 13.7.• Розв’яжіть систему рівнянь: |
x2 + y2 = 6, 4) xy = 1. |
|
3x + 4y = 24, 1) = 12; xy |
x y+ = 5, 4) − 3) (y + 5) = 6; (x |
|
y + 2x = 0, 2) 2 2 x + y − 6y = 0; |
4y − 3x = 4, 5) 2 5x + 16y = 60; |
|
x2 − xy − y2 = 19, 3) x y− = 7; 13.8.• Розв’яжіть систему рівнянь: |
x2 + 3xy + y2 − x − 2y = 3, 6) x y+ = 3. |
|
x2 − xy + y2 = 63, 1) y x− = 3; |
(x − 1) (y − 2) = 2, 3) + = 6; x y |
xy = 5; x + y = 4x;
x + 2y = 1,
2) 2 2 x + xy + 2y = 1;
5x − 2y = 3,
4) 2
3x − 8y = −5.
13.9.• Не виконуючи побудови, знайдіть координати точок перетину: 1) прямої 3x – y = 1 і параболи y = 3x2 + 8x – 3;
4
2) прямої 2x – y = 2 і гіперболи y = ![]() ;
;
x
3) прямої x + y = 1 і кола (x – 1)2 + (y + 4)2 = 16; 4) парабол y = x2 – 4x + 7 і y = 3 + 4x – 2x2.
13.10.• Доведіть, що пряма y – x = 3 є дотичною до кола (x + 5)2 + + y2 = 2, і знайдіть координати точки дотику.
13.11.• Доведіть, що:
1) пряма y = –2x – 4 і парабола y = 6x2 – 7x – 2 не перетинаються;
2) парабола y = 4x2 – 3x + 6 і пряма y = x + 5 мають одну спільну точку, знайдіть координати цієї точки;
3) параболи y = 4x2 – 3x – 24 і y = 2x2 – 5x мають дві спільні точки, знайдіть їхні координати.
13.12.• Розв’яжіть систему рівнянь:
![]()
![]() 1 − 1 = 1 , 4 + 3 = 1,
1 − 1 = 1 , 4 + 3 = 1,
1) x y 12 2) x y 2x y− = 2; x + 5y = 3.
13.13.• Розв’яжіть систему рівнянь:
![]()
![]() 1 + 1 = 3, 1 − 1 = 4,
1 + 1 = 3, 1 − 1 = 4,
1) x y 2 2) x y 5 x y− = 1; 3x y+ = 8.
13.14.• Розв’яжіть систему рівнянь:
y
x y xy+ − = 1, x + xy = −10,
|
|
x |
|
2) x y 10 x y+ = 3; |
x y2 2 + xy = 6, 6) 2x y− = 3; |
|
3) y x x2 + 4xy − 3y2 = 18; |
3 (x y+ )2 + 2 (x − 2y)2 = 5, 7) 2 (x − 2y) − x y− = 1. |
![]() 1) xy x y( + ) = 20; 5) 5y − 2xy = 13;
1) xy x y( + ) = 20; 5) 5y − 2xy = 13;
![]() x1 + 1y = 56,
x1 + 1y = 56,
4)
1 − 1 = 1;
x y 6
13.15.• Розв’яжіть систему рівнянь:
|
1) y x 2x − 3y = 3; |
4) y x 3 x2 − y2 = 72; |
|
2) x y+ x− 2y 4 4x + 5y = 3; 1 + 4 = 4, |
4 (x y− )2 + 7 (x y− ) = 15, 5) 2x + 5y = 1; |
x y (x − y)2 + 2x = 35 + 2y,
![]() 3) 6) 2 1 − 2 = 10; (x y+ ) + 2y = 3 − 2x.
3) 6) 2 1 − 2 = 10; (x y+ ) + 2y = 3 − 2x.
y x
13.16.•• Розв’яжіть систему рівнянь:
x3 + y3 = 1, x2 − y2 = 7,
1) 3)
x y+ = 1; xy = 12;
x3 − y3 = 28, 3x2 − 2y2 = 19,
2) 2 2 4)
x + xy y+ = 7; xy = −6.
13.17.•• Розв’яжіть систему рівнянь:
x3 − y3 = 56, 5x2 − y2 = −4,
1) 2)
x y− = 2; xy = 3.
13.18.•• Розв’яжіть систему рівнянь:
3y − 2xy = 2, x2 + y2 + x + y = 18,
1) x + 2xy = 5; 3) x2 − y2 + x y− = 6;
xy y+ = 30, 2x2 − 5xy + 3x − 2y = 10,
2) xy x+ = 28; 4) 5xy − 2x2 + 7x − 8y = 10.
13.19.•• Розв’яжіть систему рівнянь:
x y xy+ − = 1, xy x− = 24,
1) x y xy+ + = 9; 3) xy y− = 25;
3xy + 2x = −4, 2x2 + y2 = 66,
2) 3xy y+ = −8; 4) 2x2 − y2 = 34.
13.20.•• Розв’яжіть систему рівнянь:
|
x2 − 12xy + 36y2 = 36, 1) x + 6y = 8; |
x2 + y2 = 25, 3) xy = 12; |
|
y2 − 2xy = 32, 2) 2 2 x + 6xy + 9y = 100; |
9x2 + y2 = 10, 4) xy = −1. |
13. 21.•• Розв’яжіть систему рівнянь:
|
x2 + 10xy + 25y2 = 49, 1) x − 5y = −3; |
x2 + y2 = 10, 3) xy = 3; |
|
x2 + 4xy + 4y2 = 4x + 2y, 2) x + 2y = 4; |
x2 + 25y2 = 104, 4) xy = −4. |
•• x2 + y2 = 9,
13.22. При яких значеннях a система рівнянь
x y− = a
1) має один розв’язок; 3) не має розв’язків? 2) має два розв’язки;
•• y x− 2 = 4,
13.23. При яких значеннях k система рівнянь y kx= + 3
1) має один розв’язок; 3) не має розв’язків?
2) має два розв’язки;
13.24.* Скільки розв’язків залежно від значення a має система рівнянь:
![]() y = x , x2 + y2 = a2, y x− = 1, x2 + y2 = 4,
y = x , x2 + y2 = a2, y x− = 1, x2 + y2 = 4,
![]() 1) x2 + y a= ; 2) x = 4; 3) xy = a; 4) y x= 2 + a?
1) x2 + y a= ; 2) x = 4; 3) xy = a; 4) y x= 2 + a?
13.25.* Скільки розв’язків залежно від значення a має система рівнянь:
x2 + y2 = a, x2 + y2 = 9, x2 + y2 = a2,
1) 2) 3)
![]()
![]() y = 1; y a= − x ; xy = 4?
y = 1; y a= − x ; xy = 4?
13.26.* Дано два рівняння ax2 + x + 1 = 0 і x2 + ax + 1 = 0. Знайдіть усі значення a, при яких ці рівняння мають принаймні один спільний корінь.
![]()
13.27. Доведіть, що значення виразу 2510 – 517 кратне числу 31.
13.28. ![]() Спростіть вираз 5aa2 −+a5 : aa2+−31 − a21+a .
Спростіть вираз 5aa2 −+a5 : aa2+−31 − a21+a .
13.29. Розв’яжіть систему нерівностей: 2 (x − 3) l −3 (x + 2),
7x x
![]() 3 m1 − 2 .
3 m1 − 2 .
13.30. Відомо, що x1 і x2 — корені рівняння x2 + 6x – 2 = 0. Знайдіть значення виразу x12 + x22.
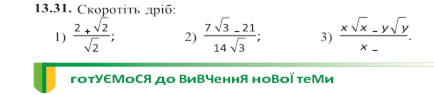
13.32. (Зі старовинного китайського трактату «Дев’ять відділів мистецтва рахунку») 5 волів і 2 барани коштують 11 таелів, а 2 воли та 8 баранів — 8 таелів. Скільки коштують окремо віл і баран?
13.33. (Задача Леонардо Пізанського (Фібоначчі)) Один говорить другому: «Дай мені 7 динаріїв, і я буду в 5 разів багатшим за тебе». А другий говорить: «Дай мені 5 динаріїв, і я буду в 7 разів багатшим за тебе». Скільки грошей у кожного?
13.34. Із села A в село B, відстань між якими дорівнює 140 км, виїхав мотоцикліст. За 20 хв до цього назустріч йому із села B у село A виїхала велосипедистка, яка зустрілася з мотоциклістом через 2 год після свого виїзду. Знайдіть швидкість кожного з них, якщо мотоцикліст за 2 год проїжджає на 104 км більше, ніж велосипедистка за 4 год.
 УЧиМоСЯ Робити неСтандаРтні кРоки
УЧиМоСЯ Робити неСтандаРтні кРоки
13.35. Чи існують 100 таких натуральних чисел, що будь-яка сума кількох із них не є квадратом натурального числа?
 Перша Всеукраїнська олімпіада юних математиків
Перша Всеукраїнська олімпіада юних математиків
Сподіваємося, що задача 13.26 вам сподобалася, і ви відчули радість успіху, розв’язавши її. Ця задача варта уваги ще й тому, що в 1961 р. її було запропоновано учасникам першої Всеукраїнської олімпіади юних математиків.
Узагалі, математичні олімпіади в Україні мають давню традицію. Перша міська олімпіада юних математиків відбулася в 1935 р.
Перша Всеукраїнська олімпіада юних математиків
у Києві. Відтоді минуло понад 80 років, і за цей час математичні олімпіади стали для багатьох талановитих школярів першим кроком на шляху до наукової творчості. Сьогодні такі імена, як О. В. Погорєлов, С. Г. Крейн, М. О. Красносельський, В. Г. Дрінфельд, відомі всьому науковому світові. Усі вони в різні роки були переможцями математичних олімпіад в Україні.
Хочемо із задоволенням зазначити, що й зараз математичні олімпіади в Україні дуже популярні. Десятки тисяч школярів нашої країни на різних етапах беруть участь у цьому математичному змаганні. До організації та проведення олімпіад залучають найкращих учених, методистів, учителів. Саме завдяки їхньому ентузіазму та професіоналізму команда України гідно представляє нашу країну на міжнародних математичних олімпіадах.
Радимо й вам, любі діти, брати участь у математичних олімпіадах. Нижче ми наводимо деякі задачі першої Всеукраїнської олімпіади юних математиків. Випробуйте свої сили.
1. Рівняння x2 + ax + b = 0 і x2 + px + q = 0 мають спільний корінь. Скласти квадратне рівняння, коренями якого є інші корені цих рівнянь.
2. ![]() Розв’язати рівняння x − 2 x − 1 + x + 3 − 4 x − 1 = 1.
Розв’язати рівняння x − 2 x − 1 + x + 3 − 4 x − 1 = 1.
3. Відстань від A до B — 999 км. Уздовж дороги стоять кілометрові стовпи, на яких відстані до A і до B написано так:
|
0 |
999 |
|
1 |
998 |
|
2 |
997 |
... |
999 |
0 |
Скільки серед цих стовпів таких, на яких є тільки дві різні цифри?

|
Олексій Васильович Погорєлов (1919 – 2002) |
Селім Григорович Крейн (1917 – 1999) |
Марк Олександрович Красносельський (1920 – 1997) |
Володимир Гершонович Дрінфельд (1954 р. н.) |
 14. Система двох рівнянь із двома змінними як математична модель прикладної задачі
14. Система двох рівнянь із двома змінними як математична модель прикладної задачі
Мабуть, немає сьогодні такої галузі знань, де б не застосовувалися досягнення математики. Фізики та хіміки, астрономи та біологи, географи та економісти, навіть мовознавці та історики використовують математичний апарат.
![]() У чому ж полягає секрет універсальності «математичного інструмента»?
У чому ж полягає секрет універсальності «математичного інструмента»?
«Ключ до розв’язання багатьох наукових задач — їх вдалий переклад мовою математики». Таку відповідь на поставлене запитання дав один із засновників і перший директор Інституту математики Академії наук України академік Д. О. Граве.
Справді, формулювання задач із різних галузей знань містять нематематичні поняття.
|
Дмитро Олександрович Граве (1863 – 1939) |
Якщо математик бере участь у розв’язуванні такої задачі, то він насамперед прагне перекласти її своєю «рідною» математичною мовою, тобто мовою виразів, формул, рівнянь, нерівно- |
стей, функцій, графіків тощо. Результат такого
перекладу називають математичною моделлю, а саму задачу — прикладною задачею.
Термін «модель» (від латин. modulus — зразок) ми використовуємо дуже часто: модель літака, модель атомного ядра, модель Сонячної системи, модель якогось процесу або явища тощо. Вивчаючи властивості моделі об’єкта, ми тим самим вивчаємо властивості самого об’єкта.
Галузь математики, яка займається побудовою та вивченням математичних моделей, називають математичним моделюванням.
Розглянемо задачі, у яких системи рівнянь другого степеня використовують як математичні моделі реальних ситуацій.
![]() Приклад 1 Із двох пунктів, відстань між якими дорівнює 18 км, вирушили одночасно назустріч одна одній дві туристки й зустрілися через 2 год. З якою швидкістю йшла кожна туристка, якщо для подолання всієї відстані між пунктами одній із них потрібно на 54 хв більше, ніж другій?
Приклад 1 Із двох пунктів, відстань між якими дорівнює 18 км, вирушили одночасно назустріч одна одній дві туристки й зустрілися через 2 год. З якою швидкістю йшла кожна туристка, якщо для подолання всієї відстані між пунктами одній із них потрібно на 54 хв більше, ніж другій?
Розв’язання. Нехай швидкість першої туристки дорівнює x км/год, а другої — y км/год, x < y. До зустрічі перша туристка пройшла 2x км, а друга — 2y км. Разом вони пройшли 18 км. Тоді 2x + 2y = 18.
Усю відстань між пунктами перша туристка проходить за
18 18
![]() год, а друга — за
год, а друга — за ![]() год. Оскільки першій туристці для проx y
год. Оскільки першій туристці для проx y
ходження цієї відстані потрібно на 54 хв = ![]() год =
год = ![]() год більше,
год більше,
![]() ніж другій, то 18 − 18 = 9 .
ніж другій, то 18 − 18 = 9 .
x y 10
Отримуємо систему рівнянь: 2x + 2y = 18,
![]() 18x − 18y = 109 .
18x − 18y = 109 .
x y+ = 9, x = 9 − y,
![]() Тоді x2 − 2y = 1 ; 9 2−y − 2y = 101 .
Тоді x2 − 2y = 1 ; 9 2−y − 2y = 101 .
10
Розв’язавши друге рівняння останньої системи, отримуємо: y1 = 5, y2 = –36. Корінь –36 не підходить за змістом задачі. Отже, y = 5, x = 4.
Відповідь: 4 км/год, 5 км/год. ◄
![]() Приклад 2 Двоє робітників можуть разом виконати деяку роботу за 10 днів. Після 6 днів спільної роботи одного з них перевели на іншу роботу, а другий продовжував працювати. Через 2 дні самостійної роботи другого з’ясувалося, що зроблено
Приклад 2 Двоє робітників можуть разом виконати деяку роботу за 10 днів. Після 6 днів спільної роботи одного з них перевели на іншу роботу, а другий продовжував працювати. Через 2 дні самостійної роботи другого з’ясувалося, що зроблено ![]() всієї роботи. За скільки днів кожний робітник може виконати всю роботу?
всієї роботи. За скільки днів кожний робітник може виконати всю роботу?
Розв’язання. Нехай перший робітник може виконати всю роботу за x днів, а другий — за y днів. За 1 день перший робітник
1 10 виконує ![]() частину роботи, а за 10 днів —
частину роботи, а за 10 днів — ![]() частину роботи. x x
частину роботи. x x
1
Другий робітник за 1 день виконує ![]() частину роботи, а за y
частину роботи, а за y
10
10 днів — ![]() частину роботи. Оскільки за 10 днів спільної праці y
частину роботи. Оскільки за 10 днів спільної праці y
![]() вони виконують усю роботу, то 10 + 10 = 1.
вони виконують усю роботу, то 10 + 10 = 1.
x y
6
Перший робітник працював 6 днів і виконав ![]() частину роботи, x
частину роботи, x
8
а другий працював 8 днів і виконав ![]() частину роботи. Оскільки y
частину роботи. Оскільки y
![]() внаслідок цього було виконано
внаслідок цього було виконано ![]() 2 роботи, то 6 + 8 = 2.
2 роботи, то 6 + 8 = 2.
3 x y 3
Отримали систему рівнянь 10 + 10 = 1,
x y
![]() 6 + 8 = 2,
6 + 8 = 2,
x y 3
розв’язком якої є пара чисел x = 15, y = 30. Отже, перший робітник може виконати всю роботу за 15 днів, а другий — за 30 днів. Відповідь: 15 днів, 30 днів. ◄
![]() Приклад 3 При діленні двоцифрового числа на добуток його цифр одержимо неповну частку 5 і остачу 2. Різниця цього числа і числа, отриманого перестановкою його цифр, дорівнює 36. Знайдіть це число.
Приклад 3 При діленні двоцифрового числа на добуток його цифр одержимо неповну частку 5 і остачу 2. Різниця цього числа і числа, отриманого перестановкою його цифр, дорівнює 36. Знайдіть це число.
Розв’язання. Нехай шукане число містить x десятків і y одиниць. Тоді воно дорівнює 10x + y. Оскільки при діленні цього числа на число xy отримуємо неповну частку 5 і остачу 2, то 10x + y = 5xy + 2.
Число, отримане перестановкою цифр даного, дорівнює 10y + x.
За умовою (10x + y) – (10y + x) = 36.
Отримуємо систему рівнянь
10x y+ = 5xy + 2, (10x y+ ) − (10y x+ ) = 36,
розв’язками якої є дві пари чисел: x = 6, y = 2 або x = 0,2, y = –3,8.
Проте друга пара не підходить за змістом задачі. Отже, шукане число дорівнює 62. Відповідь: 62. ◄
1. ![]() Що називають математичною моделлю задачі?
Що називають математичною моделлю задачі?
2. Яку задачу називають прикладною?
3. Що називають математичним моделюванням?
![]()
14.1.° Різниця двох натуральних чисел дорівнює 3, а їхній добуток на 87 більший за їхню суму. Знайдіть ці числа.
14.2.° Різниця квадратів двох натуральних чисел дорівнює 20, а сума більшого з них і подвоєного другого числа дорівнює 14. Знайдіть ці числа.
14.3.° Навколо прямокутної ділянки землі площею 2400 м2 поставили огорожу завдовжки 220 м. Знайдіть довжину та ширину ділянки.
14.4.° Периметр прямокутника дорівнює 32 см, а сума площ квадратів, побудованих на двох його сусідніх сторонах, — 130 см2. Знайдіть сторони прямокутника.
14.5.• Яке двоцифрове число в 4 рази більше за суму своїх цифр і у 2 рази більше за їхній добуток?
14.6.• Якщо деяке двоцифрове число поділити на суму його цифр, то отримаємо неповну частку 7 і остачу 6, а якщо поділити це число на добуток цифр, то отримаємо неповну частку 5 і остачу 2. Знайдіть дане число.
14.7.• Двоцифрове число в 7 разів більше за суму своїх цифр і на 52 більше за добуток цифр. Знайдіть це число.
14.8.• Різниця двох натуральних чисел дорівнює 12, а сума чисел, обернених до них, дорівнює ![]() . Знайдіть ці числа.
. Знайдіть ці числа.
14.9.• Сума двох натуральних чисел дорівнює 15, а різниця чисел, обернених до них, дорівнює ![]() . Знайдіть ці числа.
. Знайдіть ці числа.
14.10.• Гіпотенуза прямокутного трикутника дорівнює 13 см, а його площа — 30 см2. Знайдіть катети цього трикутника.
14.11.• Периметр прямокутного трикутника дорівнює 40 см, а один із катетів — 8 см. Знайдіть другий катет трикутника та його гіпотенузу.
14.12.• Площа прямокутника дорівнює 180 см2. Якщо одну його сторону зменшити на 3 см, а другу — на 2 см, то його площа дорівнюватиме 120 см2. Знайдіть початкові розміри прямокутника.
14.13.• Якщо довжину прямокутника зменшити на 3 см, а ширину збільшити на 2 см, то його площа збільшиться на 6 см2. Якщо довжину прямокутника зменшити на 5 см, а ширину збільшити на 3 см, то площа прямокутника не зміниться. Знайдіть сторони даного прямокутника.
14.14.• Із металевого листа прямокутної форми виготовили відкриту коробку. Для цього в кутах листа вирізали квадрати зі стороною 4 см. Знайдіть довжину та ширину листа, якщо його периметр дорівнює 60 см, а об’єм коробки — 160 см3.
14.15.• Два мотоциклісти виїхали одночасно з міст A і B назустріч один одному. Через годину вони зустрілися та, не зупиняючись, продовжили рухатися з тією самою швидкістю. Один із них прибув у місто A на 35 хв раніше, ніж другий — у місто B. Знайдіть швидкість кожного мотоцикліста, якщо відстань між містами становить 140 км.
14.16.• Зі станції M до станції N, відстань між якими дорівнює 300 км, вирушив товарний поїзд. Через 40 хв після цього зі станції N до станції M вийшов швидкий поїзд, який зустрівся з товарним через 2 год після свого виходу. Товарний поїзд долає відстань між станціями M і N на 3 год 20 хв довше, ніж швидкий. Знайдіть швидкість кожного поїзда.
14.17.• З одного міста в друге, відстань між якими дорівнює 240 км, виїхали одночасно автобус і автомобіль. Автобус прибув до пункту призначення на 1 год пізніше за автомобіль. Знайдіть швидкість автомобіля та швидкість автобуса, якщо за 2 год автобус проїжджає на 40 км більше, ніж автомобіль за одну годину, а їхні швидкості не перевищують 90 км/год.
14.18.• По круговій доріжці завдовжки 800 м в одному напрямі рухаються двоє ковзанярів. Один ковзаняр пробігає коло на 24 с швидше за другого й наздоганяє його через кожні 8 хв. Знайдіть швидкість кожного ковзаняра.
14.19.• Дві бригади, працюючи разом, можуть виконати виробниче завдання за 8 днів. Якщо перша бригада, працюючи самостійно, виконає ![]() завдання, а потім її змінить друга бригада, то завдання буде виконане за 20 днів. За скільки днів кожна бригада може виконати дане виробниче завдання, працюючи самостійно?
завдання, а потім її змінить друга бригада, то завдання буде виконане за 20 днів. За скільки днів кожна бригада може виконати дане виробниче завдання, працюючи самостійно?
14.20.• Дві бригади, працюючи разом, можуть розвантажити товарний поїзд за 6 год. Перша бригада виконала ![]() всієї роботи, потім її змінила друга бригада, яка й закінчила розвантаження. Уся робота була виконана за 12 год. Скільки часу потрібно кожній бригаді для самостійного розвантаження поїзда?
всієї роботи, потім її змінила друга бригада, яка й закінчила розвантаження. Уся робота була виконана за 12 год. Скільки часу потрібно кожній бригаді для самостійного розвантаження поїзда?
14.21.• Якщо відкрити одночасно дві труби, то басейн буде наповнено водою за 12 год. Якщо спочатку наповнювати басейн тільки через першу трубу протягом 5 год, а потім тільки через другу протягом 9 год, то водою буде наповнено половину басейну. За скільки годин можна наповнити басейн через кожну трубу?
14.22.• Два трактористи, працюючи разом, можуть зорати поле за 6 год. Якщо перший тракторист працюватиме самостійно 4 год, а потім його змінить другий, то цей тракторист закінчить оранку за 9 год. За який час, працюючи самостійно, може зорати поле кожен тракторист?
14.23.• При послідовному з’єднанні двох провідників опір в електричному колі становитиме 150 Ом, а при паралельному — 36 Ом. Знайдіть опір кожного провідника.
14.24.• При послідовному з’єднанні трьох провідників одного виду та одного провідника другого виду опір в електричному колі становитиме 18 Ом. Якщо паралельно з’єднати по одному провіднику першого та другого видів, то за напруги 24 В сила струму в електричному колі становитиме 10 А. Знайдіть опір провідника кожного виду.
14.25.•• Човен проплив по річці від пристані A до пристані B і повернувся назад за 6 год. Знайдіть швидкість течії річки, якщо 2 км за течією річки човен пропливає за той самий час, що й 1 км проти течії, а відстань між пристанями A і B становить 16 км.
14.26.•• Катер проходить 48 км проти течії річки та 30 км за течією річки за 3 год, а 15 км за течією — на 1 год швидше, ніж 36 км проти течії. Знайдіть власну швидкість катера та швидкість течії.
14.27.•• Із міст A і B, відстань між якими 40 км, одночасно назустріч одна одній виїхали на велосипедах Галина та Катерина. Галина прибула до міста B через 40 хв, а Катерина — до міста A через 1,5 год після зустрічі. Знайдіть швидкість руху кожної дівчини.
144
14.28.•• З одного села одночасно в одному напрямі вирушили пішки Петро та Василь. Швидкість руху Петра становила 3 км/год, а Василя — 4 км/год. Через півтори години із цього села виїхала на велосипеді Ірина, яка наздогнала Василя через 15 хв після того, як наздогнала Петра. Знайдіть швидкість руху Ірини.
14.29.•• Відстань між пристанями A і B дорівнює 28 км. Вирушивши від пристані A до пристані B, через 2 год після початку руху катер зустрів пліт, відправлений від пристані B за течією річки за 2 год до початку руху катера. Знайдіть швидкість течії річки та власну швидкість катера, якщо катер проходить відстань від A до B і повертається назад за 4 год 48 хв.
14.30.•• Маса зливка одного металу дорівнює 336 г, а зливка другого — 320 г. Об’єм зливка першого металу на 10 см3 менший від об’єму другого, а густина першого — на 2 г/см3 більша за густину другого. Знайдіть густину кожного металу.
14.31.•• Модуль рівнодіючої двох сил, що прикладені до однієї точки під прямим кутом, дорівнює 25 Н. Якщо модуль однієї сили зменшити на 8 Н, а другої збільшити на 4 Н, то модуль їхньої рівнодіючої не зміниться. Знайдіть модулі даних сил.
14. 32.•• По двох сторонах прямого кута в напрямку до його вершини рухаються два тіла. Перше тіло рухається зі швидкістю 12 м/хв, а друге — зі швидкістю 16 м/хв. У певний момент часу відстань між тілами становила 100 м. Через 2 хв після цього відстань між тілами стала дорівнювати 60 м. На якій відстані від вершини прямого кута знаходилося кожне тіло в перший зафіксований момент часу?
![]()
14.33. Спростіть вираз:
1) ![]() a2 2− 3a − a2 1+ 3a − aa2+−19;
a2 2− 3a − a2 1+ 3a − aa2+−19;
3 3b− 2 b2 + 16b+ 12
2) b− 2 − b2 + 2b+ 4 − b3 − 8 .
14.34. Звільніться від ірраціональності в знаменнику дробу:
4a 3 5 2
1) ; 2) ; 3) ; 4) .
![]()
![]()
![]()
![]() 5 a b − 1 6 − 1 2 7 − 3 2
5 a b − 1 6 − 1 2 7 − 3 2
14.35. Розв’яжіть нерівність: 1) 1 1 5, ( x − 4) m 0 2 10, ( x + 13);
![]() 2) 0 6, − 5y < 0 5, − 5y.
2) 0 6, − 5y < 0 5, − 5y.
4 6
14.36. Знайдіть найбільший цілий розв’язок нерівності (2x + 1) (x + 4) – 3x (x + 2) > 0.
14.37. При яких значеннях змінної має зміст вираз
![]() 12 − 5x + 2x + 1?
12 − 5x + 2x + 1?
14.38. Знайдіть проміжок спадання функції:
1) y = 2x2 + 10x – 9; 2) y = 5x – 3x2.
14.39. 14 грудня 1840 року в Парижі комісія у складі академіківматематиків зібралася для вивчення математичних здібностей хлопчика Анрі Мондьо, який феноменально виконував обчислення. Розв’яжіть одну із запропонованих Мондьо задач, яку хлопчик розв’язав усно: «Які два натуральних числа треба взяти,
щоб різниця їхніх квадратів дорівнювала 133?»
ЗаВданнЯ № 3 «ПеРеВіРте Себе» В теСтоВій фоРМі
1. При яких значеннях x виконується нерівність x2 > 4?
А) x > 2; В) x < –2 або x > 2;
Б) x > 2 або x > –2; Г) –2 < x < 2.
2. Яка множина розв’язків нерівності x2 + 8x − 9 l 0?
А) (−×; −9) Ÿ (1; +×); В) (−×; −1) Ÿ (9; +×);
Б) (−×; −9] Ÿ [1; +×); Г) (−×; −1] Ÿ [9; +×).
3. Скільки цілих розв’язків має нерівність 3x2 + 5x – 8 < 0?
А) 3; Б) 4; В) 5; Г) 6.
4. Яка з даних нерівностей виконується при всіх дійсних значеннях змінної?
А) x2 – 14x + 49 > 0; В) x2 – 3x + 4 > 0; Б) −3x2 + x + 2 m 0; Г) –x2 + 7x – 10 < 0.
5. Яка область визначення функції f x( ) = ![]() ?
?
А) (−×; 0] Ÿ [2; +×); В) [0; 2];
Б) (−×; 0) Ÿ (2; +×); Г) (0; 2).
6. Укажіть нерівність, яка не має розв’язків.
А) x2 – 6x + 10 < 0; В) –3x2 + 8x + 3 < 0;
Б) –5x2 + 3x + 2 > 0; Г) –x2 – 10x > 0.
7. Пари чисел (x1; y1) і (x2; y2) є розв’язками системи рівнянь y x− = 2,
xy − y = 10. Чому дорівнює значення виразу x1y1 + x2y2?
А) 23; Б) 7; В) 35; Г) –26.
x2 + y2 = 5,
8. Які фігури є графіками рівнянь системи xy = −3?
А) Пряма та парабола; В) коло та гіпербола; Б) коло та парабола; Г) парабола та гіпербола.
x2 − y = 4,
9. Скільки розв’язків має система рівнянь
x y+ = 1?
А) Жодного розв’язку; В) два розв’язки;
Б) один розв’язок; Г) чотири розв’язки.
Завдання № 3 «Перевірте себе» в тестовій формі 10. Якого найбільшого значення набуває вираз x + y, якщо пара
x y− = 5,
чисел (x; y) є розв’язком системи рівнянь x2 + 2xy y− 2 = −7?
А) 1; Б) 6; В) 0; Г) –5.
x2 + 1y = 4,
11. ![]() Пара чисел (a; b) є розв’язком системи рівнянь Знай1 − 3 = 9.
Пара чисел (a; b) є розв’язком системи рівнянь Знай1 − 3 = 9.
x y
діть значення виразу a – b.
А) 5; Б) 1; В) ![]() ; Г)
; Г) ![]() .
.
12. Пари чисел (x1; y1) і (x2; y2) є розв’язками системи рівнянь 2x xy− = 5,
y xy+ = 6. Знайдіть значення виразу | x1y1 – x2y2 |.
А) 1; Б) 11; В) 70; Г) 10.
13. Периметр прямокутника дорівнює 34 см, а його діагональ — 13 см. Нехай сторони прямокутника дорівнюють x см і y см. Яка з наведених систем рівнянь є математичною моделлю ситуації, описаної в умові?
|
x y+ = 34, А) 2 2 x + y = 13; |
x y+ = 34, В) 2 2 x + y = 169; |
2 (x y+ ) = 34, 2 (x y+ ) = 34,
Б) x2 + y2 = 13; Г) x2 + y2 = 169.
14. Відстань між двома містами, яка дорівнює 120 км, легковий автомобіль проїжджає на 30 хв швидше, ніж вантажівка. Відомо, що за 2 год вантажівка проїжджає на 40 км більше, ніж легковий автомобіль за 1 год.
Нехай швидкість вантажівки дорівнює x км/год, а легкового автомобіля — y км/год. Яка з наведених систем рівнянь є математичною моделлю ситуації, описаної в умові?
|
А) x y 2x y− = 40; |
В) x y 2 2x y− = 40; |
|
Б) y x 2x y− = 40; |
Г) y x 2 2x y− = 40. |
15. Дві працівниці можуть виконати комп’ютерний набір тексту підручника алгебри за 8 днів. Якщо перша працівниця набере ![]() тексту, а потім друга працівниця завершить набір, то весь
тексту, а потім друга працівниця завершить набір, то весь
текст підручника буде набрано за 16 днів.
Нехай перша працівниця може набрати текст підручника за x днів, а друга — за y днів. Яка з наведених систем рівнянь є математичною моделлю ситуації, описаної в умові?
|
x y+ = 8, А) 2 1 x + y = 16; |
x y+ = 8, В) 1 2 x + y = 16; |
3 3 3 3
![]()
![]() x1 + 1y = 18, x1 + 1y = 18,
x1 + 1y = 18, x1 + 1y = 18,
Б) Г)
2 + 1 = 1 ; 23 x + 13 y = 16.
3x 3y 16
16. При яких значеннях b рівняння 3x2 – bx + 3 = 0 не має коренів?
А) –6 < b < 6; В) b > 6; Б) b < 6; Г) b < –6 або b > 6.
x2 + y2 = 25,
17. При якому значенні a система рівнянь має єдиний x y− = a
розв’язок?
А) a = 5; В) a = –5 або a = 5;
![]()
![]()
![]() Б) a = 5 2; Г) a = −5 2 або a = 5 2.
Б) a = 5 2; Г) a = −5 2 або a = 5 2.
18. При яких значеннях a нерівність ax2 – 2x + a < 0 не має розв’язків?
А) a < –1 або a > 1; В) –1 < a < 1;
Б) al1; Г) таких значень не існує.
Головне в параграфі 2
 ! гоЛоВне В ПаРагРафі 2
! гоЛоВне В ПаРагРафі 2
Функція
Нехай X — множина значень незалежної змінної, Y — множина значень залежної змінної. Функція — це правило, за допомогою якого за кожним значенням незалежної змінної з множини X можна знайти єдине значення залежної змінної з множини Y.
Нуль функції
Значення аргументу, при якому значення функції дорівнює нулю, називають нулем функції.
Проміжок знакосталості функції
Проміжок, на якому функція набуває значень однакового знака, називають проміжком знакосталості функції.
Зростання і спадання функції
Функцію називають зростаючою на деякому проміжку, якщо для будь-яких значень аргументу із цього проміжку більшому значенню аргументу відповідає більше значення функції. Функцію називають спадною на деякому проміжку, якщо для будь-яких значень аргументу із цього проміжку більшому значенню аргументу відповідає менше значення функції.
Побудова графіка функції y = kf (x)
Графік функції y = kf (x) можна отримати з графіка функції y = f (x) у результаті розтягнення в k разів від осі абсцис, якщо 1
k > 1, або в результаті стискання в ![]() раза до осі абсцис, якщо k
раза до осі абсцис, якщо k
0 < k < 1.
Побудова графіка функції y = f (x) + b
Графік функції y = f (x) + b можна отримати в результаті паралельного перенесення графіка функції y = f (x) уздовж осі ординат на b одиниць угору, якщо b > 0, і на –b одиниць униз, якщо b < 0.
Побудова графіка функції y = f (x + a)
Графік функції y = f (x + a) можна отримати в результаті паралельного перенесення графіка функції y = f (x) уздовж осі абсцис на a одиниць уліво, якщо a > 0, і на –a одиниць управо, якщо a < 0.
Квадратична функція
Функцію, яку можна задати формулою виду y = ax2 + bx + c, де x — незалежна змінна, a, b і c — деякі числа, причому a ≠ 0, називають квадратичною.
Квадратні нерівності
Нерівності виду ax2 + bx + c > 0, ax2 + bx + c < 0, ax2 + bx c+ l 0, ax2 + bx c+ m 0, де x — змінна, a, b і c — деякі числа, причому
a ≠ 0, називають квадратними.
Схематичне розміщення параболи y = ax2 + bx + c відносно осі абсцис
|
|
D > 0 |
D = 0 |
D < 0 |
|
a > 0 |
|
|
|
|
a < 0 |
|
|
|
§ 3 числові ПослідовНості
• ![]() Ви ознайомитеся з такими новими поняттями, як послідовність, n-й член послідовності, арифметична й геометрична прогресії, скінченні та нескінченні послідовності; дізнаєтеся, які є способи задання числових послідовностей.
Ви ознайомитеся з такими новими поняттями, як послідовність, n-й член послідовності, арифметична й геометрична прогресії, скінченні та нескінченні послідовності; дізнаєтеся, які є способи задання числових послідовностей.
• Навчитеся знаходити члени прогресій, обчислювати суми nперших членів прогресій.
15. Числові послідовності
Часто в повсякденному житті нам трапляються об’єкти, з якими зручно мати справу, якщо їх попередньо пронумерувати. Наприклад, номери мають місяці та квартали року, дні тижня, під’їзди та квартири будинку, вагони поїзда, і навіть кожен учень вашого класу має свій порядковий номер у класному журналі.
Об’єкти, які пронумеровано поспіль натуральними числами 1, 2, 3, ..., n, ..., утворюють послідовності.
Так, можна говорити про послідовності сторінок у книзі, букв у слові, поверхів у будинку тощо.
Об’єкти, які утворюють послідовність, називають членами послідовності. Кожний член послідовності має свій номер. Наприклад, січень — це перший член послідовності місяців року, число 3 — другий член послідовності простих чисел. Узагалі, якщо член послідовності має номер n, то його називають nм членом послідовності.
Якщо членами послідовності є числа, то таку послідовність називають числовою.
Наведемо приклади числових послідовностей.
1, 2, 3, 4, 5, ... — послідовність натуральних чисел;
2, 4, 6, 8, 10, ... — послідовність парних чисел;
0,3; 0,33; 0,333; ... — послідовність десяткових наближень дробу ![]() ;
;
19, 38, 57, 76, 95 — послідовність двоцифрових чисел, кратних 19; –1, –2, –3, –4, –5, ... — послідовність від’ємних цілих чисел.
Надалі ми розглядатимемо тільки числові послідовності.
Послідовності бувають скінченними і нескінченними. Наприклад, послідовність парних натуральних чисел — це нескінченна послідовність, а послідовність двоцифрових чисел, кратних 19, — це скінченна послідовність.
Для позначення членів послідовності використовують букви з індексами:
a1, a2, a3, ..., an, ... .
Індекс указує порядковий номер члена послідовності. Для позначення самої послідовності використовують запис (an). Наприклад, якщо (pn) — послідовність простих чисел, то p1 = 2, p2 = 3, p3 = 5, p4 = 7, p5 = 11 і т. д.
Послідовність вважають заданою, якщо кожний її член можна визначити за його номером.
Ознайомимося з основними способами задання послідовності.
Розглянемо послідовність, у якої перший член дорівнює 1, а кожний наступний член на 3 більший за попередній. Такий спосіб задання послідовності називають описовим. Його можна проілюструвати за допомогою запису з трьома крапками, виписавши кілька перших членів послідовності у порядку зростання номерів:
1, 4, 7, 10, 13, 16, 19, ... .
Цей запис доцільно застосовувати тоді, коли зрозуміло, які числа мають бути записані замість трьох крапок.
Наприклад, у послідовності, яку ми розглядаємо, зрозуміло, що після числа 19 має бути записано число 22.
Якщо послідовність є скінченною, то її можна задати за допомогою таблиці. Наприклад, наведена таблиця задає послідовність кубів одноцифрових натуральних чисел:
|
n |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
an |
1 |
8 |
27 |
64 |
125 |
216 |
343 |
512 |
729 |
Послідовності можна задавати за допомогою формул. Наприклад, рівність xn = 2n, де змінна n набуває всіх натуральних значень, задає послідовність (xn) натуральних степенів числа 2:
2, 4, 8, 16, 32, ... .
У таких випадках говорять, що послідовність задано за допомогою формули nго члена послідовності.
Розглянемо кілька прикладів.
Формула an = 2n – 1 задає послідовність натуральних непарних чисел:
1, 3, 5, 7, 9, ... .
15. Числові послідовності
![]()
Формула yn = (–1)n задає послідовність (yn), у якій усі члени з непарними номерами дорівнюють –1, а з парними номерами дорівнюють 1:
–1, 1, –1, 1, –1, ... .
Формула cn = 7 задає послідовність (cn), усі члени якої дорівнюють числу 7:
7, 7, 7, 7, 7, ... .
Наведені способи задання послідовностей допомагають простежити зв’язок між поняттями «функція» і «послідовність».
Розглянемо функцію y = f (x), областю визначення якої є множина натуральних чисел або множина n перших натуральних чисел. Тоді функція f задає нескінченну послідовність f (1), f (2), ..., f (n), ... або скінченну послідовність f (1), f (2), ..., f (n).
Наприклад, якщо функцію f, областю визначення якої є множина натуральних чисел, задано формулою f (x) = x2, то ця функція задає послідовність квадратів натуральних чисел:
1, 4, 9, 16, 25, ... .
Нерідко послідовність задають правилом, яке дає змогу знайти наступний член, знаючи попередній.
Розглянемо послідовність (an), перший член якої дорівнює 1, а кожний наступний член послідовності в 3 рази більший за попередній. Маємо:
1, 3, 9, 27, 81, ... .
Цю саму послідовність також можна визначити такими умовами: a1 = 1, an + 1 = 3an.
Ці рівності вказують перший член послідовності та правило, користуючись яким за кожним членом послідовності можна знайти наступний за ним член:
a1 = 1,
a2 = 3a1 = 3, a3 = 3a2 = 9,
a4 = 3a3 = 27, і т. д.
Формулу, яка виражає член послідовності через один або кілька попередніх членів, називають рекурентною формулою (від латин. recurro — повертатися). У наведеному прикладі це формула an + 1 = 3an. Умови, які визначають перший або кілька перших членів, називають початковими умовами. У розглядуваному прикладі початкова умова — це рівність a1 = 1.
Спосіб задання послідовності за допомогою початкових умов і рекурентної формули називають рекурентним способом задання послідовності.
При рекурентному способі задання послідовності перший або кілька перших членів послідовності є заданими, а всі інші обчислюють один за одним. Із цієї точки зору спосіб задання послідовності формулою n-го члена видається більш зручним: за його допомогою можна одразу знайти потрібний член послідовності, знаючи лише його номер.
![]() Приклад Послідовність (cn) задано формулою n-го члена cn = 37 – 3n. Чи є членом цієї послідовності число: 1) 19; 2) –7? У разі ствердної відповіді вкажіть номер цього члена.
Приклад Послідовність (cn) задано формулою n-го члена cn = 37 – 3n. Чи є членом цієї послідовності число: 1) 19; 2) –7? У разі ствердної відповіді вкажіть номер цього члена.
Розв’язання. 1) Якщо число 19 є членом даної послідовності, то існує таке натуральне значення n, при якому виконується рівність 37 – 3n = 19. Звідси 3n = 18; n = 6. Отже, число 19 є шостим членом послідовності (cn).
2) Маємо: 37 – 3n = –7; 3n = 44; n = 14![]() . Оскільки число 14
. Оскільки число 14![]() не є натуральним, то число –7 не є членом даної послідовності.
не є натуральним, то число –7 не є членом даної послідовності.
Відповідь: 1) Так, n = 6; 2) ні. ◄
1. ![]() Що утворюють об’єкти, які пронумеровано поспіль натуральними числами?
Що утворюють об’єкти, які пронумеровано поспіль натуральними числами?
2. Як називають об’єкти, які утворюють послідовність?
3. Як називають член послідовності, який має номер n?
4. Яку послідовність називають числовою?
5. У якому разі послідовність вважають заданою?
6. Які способи задання послідовності ви знаєте?
7. Поясніть, що таке формула n-го члена послідовності.
8. Який зв’язок між поняттями «функція» і «послідовність»?
9. Поясніть, що таке рекурентна формула.
ВПРаВи
15.1.° Запишіть у порядку зростання п’ять перших членів послідовності:
1) двоцифрових чисел, кратних числу 4;
2) неправильних звичайних дробів із чисельником 11; 3) натуральних чисел, що дають при діленні на 8 остачу 5.
Укажіть, скінченними чи нескінченними є ці послідовності.
15. Числові послідовності
![]()
15.2.° Послідовність (an) є послідовністю трицифрових чисел, кратних числу 5, узятих у порядку зростання. Заповніть таблицю:
|
n |
1 |
2 |
3 |
4 |
5 |
6 |
|
an |
|
|
|
|
|
|
15.3.° Знайдіть чотири перших члени послідовності (an), заданої формулою n-го члена:
1) an = n + 4; 2) an = 4n – 3; 3) an = ![]() n2n+ 1; 4) an =
n2n+ 1; 4) an = ![]() 2nn .
2nn .
15.4.° Знайдіть другий, сьомий і сотий члени послідовності (bn), заданої формулою n-го члена:
![]() 10 2 + 2n; 4) bn = (–1)n + 1.
10 2 + 2n; 4) bn = (–1)n + 1.
1) bn = ; 2) bn = 5 – 2n; 3) bn = n n
15.5.° Послідовність (cn) задано формулою n-го члена cn = (–1)n . 5.
Знайдіть:
1) c1; 2) c8; 3) c2k; 4) c2k + 1; 5) ck + 2.
15.6.° Послідовність (xn) задано формулою n-го члена xn = 3n + 1. Знайдіть:
1) x1; 2) x7; 3) x20; 4) x300; 5) xk + 1.
15.7.° Знайдіть п’ять перших членів послідовності (an), якщо:
1) a1 = 4, an + 1 = an + 3;
2) a1 = –2, a2 = 6, an + 2 = 3an + an + 1.
15.8.° Знайдіть п’ять перших членів послідовності (bn), якщо:
bn ;
1) b1 = 18, bn+1 = −
3
2) b1 = –1, b2 = 2, bn + 2 = bn2 + 2bn + 1.
15.9.• Послідовність (an) задано формулою n-го члена an = 7n + 2. Чи є членом цієї послідовності число: 1) 23; 2) 149; 3) 47? У разі ствердної відповіді вкажіть номер цього члена.
15.10.• Послідовність (bn) задано формулою n-го члена bn = n2 – 4. Чи є членом цієї послідовності число: 1) 5; 2) 16; 3) 77? У разі ствердної відповіді вкажіть номер цього члена.
15.11.• Скільки від’ємних членів містить послідовність (xn), задана формулою n-го члена xn = 6n – 50?
15.12.• Знайдіть номер першого від’ємного члена послідовності (yn), заданої формулою n-го члена yn = 38 – 3n.
15.13.•• Послідовність (an) задано формулою n-го члена an = = n2 – 3n – 8. Знайдіть номери членів цієї послідовності, які менші від 10.
15.14.•• Послідовність (bn) задано формулою n-го члена bn = –n2 + + 15n – 20. Скільки членів цієї послідовності більші за 16?
15.15.•• Підберіть одну з можливих формул n-го члена послідовності, першими членами якої є числа:
1 2 3 4
1) ![]() 1, 4, 9, 25, ...; 3) 0, , , , , ...;
1, 4, 9, 25, ...; 3) 0, , , , , ...;
2 3 4 5
2) 5, 8, 11, 14, 17, ...; 4) 0, 2, 0, 2, 0, ... .
15. 16.•• Підберіть одну з можливих формул n-го члена послідовності, першими членами якої є числа:
![]()
![]() 3x2 − 7x+ 2 5xy− 5x− 2y+ 2 1) 2 − 6x ; 2) 10x2 − 9x+ 2 .
3x2 − 7x+ 2 5xy− 5x− 2y+ 2 1) 2 − 6x ; 2) 10x2 − 9x+ 2 .
15.18. Знайдіть область визначення функції:
2 −x 6 − 5x x− 2
1) y = ; 2) y = . x+ 2 x− 1
15.19. Графіком квадратичної функції є парабола з вершиною в по-
чатку координат, яка проходить через точку A −1; − ![]() 1 . За-
1 . За-
4
дайте цю функцію формулою.
15.20. Робітник планував за деякий час виготовити 160 деталей. Проте він закінчив роботу на 3 год раніше, ніж планував, оскільки виготовляв щогодини на 12 деталей більше, ніж було заплановано. Скільки деталей виготовляв робітник щогодини?
15.21. Морська вода містить 5 % солі. Скільки прісної води треба додати до 40 кг морської води, щоб концентрація солі склала 2 %?
15.22. За перший день хлопчик прочитав 25 % усієї книжки, за другий — 72 % від кількості сторінок, що залишилася, а за третій — решту 84 сторінки. Скільки сторінок у книжці?
Про кролів, соняшники, соснові шишки та золотий переріз
![]()
15.23. Розглядаються квадратичні функції y = x2 + px + q, для яких p + q = 5. Доведіть, що параболи, які є графіками цих функцій, перетинаються в одній точці.
![]() Про кролів, соняшники, соснові шишки
Про кролів, соняшники, соснові шишки
та золотий переріз
Розглянемо послідовність (un), яку задано рекурентно такими співвідношеннями:
u1 = u2 = 1, un + 2 = un + 1 + un.
Запишемо кілька її перших членів:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, ... .
Члени цієї послідовності називають числами Фібоначчі. Така назва пов’язана з тим, що італійський математик Леонардо Пізанський (Фібоначчі), розв’язуючи популярну в XII ст. задачу про чисельність потомства пари кролів, першим звернув увагу на чудові властивості цієї послідовності. У цій задачі чисельність потомства кролів збільшується так: кожна доросла пара кролів щомісяця приводить пару кроленят, які через місяць також починають давати потомство. На рисунку 15.1 кількість пар кролів відповідає послідовності чисел Фібоначчі.
На числа Фібоначчі можна натрапити в різних ситуаціях. Уявіть собі, що ви йдете доріжкою, вимощеною квадратними плитками в один ряд, ступаючи кожного разу на наступну плитку або через
Леонардо Пізанський (Фібоначчі)
![]() (12–13 ст.)
(12–13 ст.)
Італійський математик. Подорожуючи країнами
Сходу, ознайомився з досягненнями арабських математиків і сприяв поширенню цих знань у Європі. Його основні праці: «Liber Abaci» (1202) — трактат про арифметику й алгебру,
«Practica Geometriae» (1220) започаткували застосування алгебраїчних методів у геометрії.
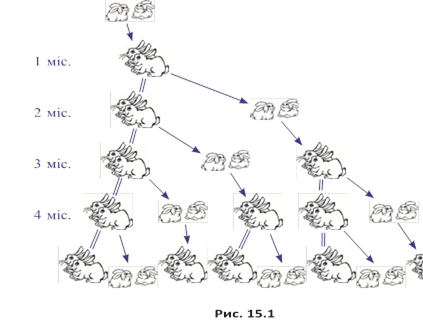
одну. Тоді кількість способів пройти доріжку з n плиток дорівнює n-му члену послідовності Фібоначчі (перевірте це самостійно, наприклад, для випадку n = 8).
Навіть деякі явища природи пов’язані із числами Фібоначчі.
Якщо подивитися на насіння в голівці соняшника або ромашки, то можна побачити, що зернятка розміщені у вигляді двох сімейств спіралей, які закручуються в протилежних напрямках. Кількість спіралей у цих сімействах є сусідніми членами послідовності Фібоначчі. Зазвичай для соняшника ці числа дорівнюють 34 і 55, проте трапляються й гіганти з 89 і 144 спіралями. Подібну властивість[5] можна виявити в структурі соснових шишок. Те саме явище спостерігається й на плодах ананаса, де спіралей, як правило, буває 8 і 13.
Якщо в послідовності Фібоначчі для кожного натурального n
un+1 обчислити відношення ![]() , то отримаємо послідовність 1; 2; 1,5; un
, то отримаємо послідовність 1; 2; 1,5; un
1,(6); 1,6; 1,625; 1,(615384); 1,61(904761); ... .

Цій послідовності притаманна така властивість: зі зростанням номерів її члени все менше й менше відрізняються від числа
![]() , .
, .
Ще в давнину із цим числом люди пов’язували своє уявлення про красу та гармонію. Грецькі скульптори добре знали про відповідність правильних пропорцій людського тіла цьому магічному числу. І недаремно античні зодчі використовували його у своїх безсмертних творіннях. Так, відношення довжини Парфенона[6] до його висоти наближено дорівнює 1,618. Геній епохи Відродження Леонардо да Вінчі вважав, що з багатьох відношень, які використовує Творець, існує одне, єдине й неповторне. Саме його він назвав «золотим перерізом».
Французький учений Жак Біне (1786–1856) указав формулу n-го члена послідовності Фібоначчі:
![]() n n
n n
un = .
Важко повірити, що ця формула задає натуральні числа. Проте це так.

Розглянемо такі послідовності:
2, 7, 12, 17, 22, 27, ...;
1; 1,5; 2; 2,5; 3; 3,5; ...; 3, 1, –1, –3, –5, –7, ... .
Їм притаманна така характерна особливість: кожний наступний член послідовності отримано в результаті додавання до попереднього одного й того самого числа. Для першої послідовності це число дорівнює 5, для другої це число дорівнює 0,5, для третьої це число дорівнює –2.
З подібними послідовностями людям доводилося мати справу ще в давні часи, коли вони рахували предмети парами, п’ятірками, десятками, дюжинами тощо. Такі послідовності називають арифметичними прогресіями (від лат. progressio — рух уперед).
Означення. Арифметичною прогресією називають послідовність, кожний член якої, починаючи з другого, дорівнює попередньому члену, до якого додано одне й те саме число.
Число, яке дорівнює різниці наступного й попереднього членів послідовності, називають різницею арифметичної прогресії та позначають буквою d (першою буквою латинського слова differentia —
різниця).
Отже, якщо (an) — арифметична прогресія з різницею d, то d = a2 – a1 = a3 – a2 = a4 – a3 = ...,
тобто для будь-якого натурального n виконується рівність an + 1 – an = = d. Звідси
an + 1 = an + d.
Отже, арифметичну прогресію можна задати рекурентно:
a1 = a, an + 1 = an + d
Таким чином, щоб задати арифметичну прогресію, потрібно вказати її перший член і різницю.
Наведемо кілька прикладів.
Якщо a1 = 2 і d = 5, то отримаємо арифметичну прогресію, подану на початку пункту:
2, 7, 12, 17, 22, 27, ... .
Якщо a1 = 1 і d = 2, то отримаємо арифметичну прогресію — послідовність непарних чисел:
1, 3, 5, 7, 9, 11, ... .
Ми навели приклади арифметичних прогресій, у яких різниця є додатним числом. Проте різниця може бути від’ємним числом і навіть нулем. Так, послідовність 5, 5, 5, 5, ..., усі члени якої рівні між собою, є арифметичною прогресією, у якої a1 = 5, d = 0.
Покажемо, як можна задати арифметичну прогресію за допомогою формули n-го члена.
З означення арифметичної прогресії (an) випливає: a2 = a1 + d;
a3 = a2 + d = (a1 + d) + d = a1 + dæ2;
a4 = a3 + d = (a1 + dæ2) + d = a1 + dæ3; a5 = a4 + d = (a1 + dæ3) + d = a1 + dæ4.
Ці приклади допомагають побачити таку закономірність: щоб знайти деякий член арифметичної прогресії, можна до першого члена додати добуток різниці d і числа, яке на 1 менше від номера шуканого члена. Звідси, наприклад, a6 = a1 + dæ5, a7 = a1 + dæ6, і взагалі
an = a1 + d (n – 1)
Записану рівність називають формулою nго члена арифметичної прогресії.
Установимо важливу властивість членів арифметичної прогре-
сії (an).
Маємо:
a1 +a3 . a2 – a1 = a3 – a2, звідси 2a2 = a1 + a3; a2 =
2
a2 +a4 . a3 – a2 = a4 – a3, звідси 2a3 = a2 + a4; a3 =
2
Узагалі, для будь-якого натурального n, більшого за 1, можна записати: an – an – 1 = an + 1 – an, звідки
|
a a = n_1 +an+1
n 2 |
Будь-який член арифметичної прогресії, крім першого (і останнього, якщо прогресія є скінченною), дорівнює середньому арифметичному двох сусідніх із ним членів.
![]() Приклад Доведіть, що послідовність (an), задана формулою n-го члена an = 9n – 2, є арифметичною прогресією.
Приклад Доведіть, що послідовність (an), задана формулою n-го члена an = 9n – 2, є арифметичною прогресією.
Розв’язання. Розглянемо різницю двох довільних послідовних членів послідовності:
an + 1 – an = 9 (n + 1) – 2 – (9n – 2) = 9n + 9 – 2 – 9n + 2 = 9.
Отже, при будь-якому натуральному n виконується рівність an + 1 = an + 9, тобто кожний член даної послідовності, починаючи з другого, дорівнює попередньому члену, до якого додано одне й те саме число 9. Таким чином, дана послідовність є арифметичною прогресією. ◄
1. Яку послідовність називають арифметичною прогресією?
2. ![]() Яке число називають різницею арифметичної прогресії? Як позначають це число?
Яке число називають різницею арифметичної прогресії? Як позначають це число?
3. Що потрібно вказати, щоб задати арифметичну прогресію?
4. Як можна задати арифметичну прогресію рекурентно?
5. Який вигляд має формула n-го члена арифметичної прогресії?
6. Як пов’язані між собою будь-який член арифметичної прогресії та сусідні з ним члени?
ВПРаВи
16.1.° Серед поданих послідовностей укажіть арифметичні прогресії:
1) 3, –6, 12, –24; 3) 5, 10, 5, 10; 5) –5, –3, –1, 1; 2) 4, 8, 12, 16; 4) 42, 39, 36, 33; 6) 1,2; 1,3; 1,5; 1,6.
16.2.° Чи є арифметичною прогресією послідовність (у разі ствердної відповіді вкажіть різницю прогресії):
1) 24, 22, 20, 18; 2) 16, 17, 19, 23; 3) –3, 2, 7, 12?
16.3.° Знайдіть чотири перші члени арифметичної прогресії, перший член якої дорівнює 1,2, а різниця становить –0,3.
16.4.° Перший член арифметичної прогресії дорівнює –7,4, а різниця становить 1,8. Знайдіть п’ять перших членів прогресії.
16.5.° Перший член арифметичної прогресії (an) дорівнює 4, а різниця становить 0,4. Знайдіть: 1) a3; 2) a11; 3) a32.
16.6.° Перший член арифметичної прогресії (an) дорівнює 17, а різниця становить –2. Знайдіть: 1) a4; 2) a15; 3) a60.
16.7.° Знайдіть різницю та двісті перший член арифметичної прогресії 2,6; 2,9; 3,2; ... .
16.8.° Чому дорівнює різниця арифметичної прогресії (an), якщо a6 = –2, a7 = 6?
16.9.° Знайдіть різницю арифметичної прогресії (an), якщо a8 = 3, a9 = –12.
16.10.° Знайдіть різницю арифметичної прогресії (xn), якщо x1 = 2, x8 = –47.
16.11.° Знайдіть перший член арифметичної прогресії (yn), якщо y17 = 22, а різниця прогресії d = 0,5.
16.12.• Знайдіть формулу n-го члена арифметичної прогресії:
1) –5, –7, –9, –11, ...; 3) a2, 2a2, 3a2, 4a2, ...;
1 1 1
2) ![]() 2, 2 , 2 , 2 , ...; 4) a + 3, a + 1, a – 1, a – 3, ... .
2, 2 , 2 , 2 , ...; 4) a + 3, a + 1, a – 1, a – 3, ... .
6 3 2
16.13.• Чи є членом арифметичної прогресії (cn):
1) число 20,4, якщо c1 = 11,4, а різниця прогресії d = 0,6; 2) число 38, якщо c1 = 8, а різниця прогресії d = 1,4?
У разі ствердної відповіді вкажіть номер цього члена.
16.14.• Знайдіть номер члена арифметичної прогресії 8,1; 8,5; 8,9; 9,3; ..., який дорівнює 13,7.
16.15.• Знайдіть другий член арифметичної прогресії, якщо перший і третій члени дорівнюють відповідно –6 і 12.
16.16.• Восьмий і десятий члени арифметичної прогресії дорівнюють відповідно 3,5 і 2,7. Чому дорівнює дев’ятий член прогресії?
16.17.• Знайдіть перший член арифметичної прогресії (bn), якщо b5 = 11, b11 = –7.
16.18.• Чому дорівнює різниця арифметичної прогресії (xn), якщо x8 = 58, x15 = 16?
16.19.• Як зміниться різниця скінченної арифметичної прогресії, якщо переставити її члени у зворотному порядку?
16.20.• Скільки додатних членів містить арифметична прогресія 5,2; 4,9; 4,6; ...?
16.21.• Який номер має перший додатний член арифметичної прогресії –10,2; –9,5; –8,8; ...?
16.22.• Знайдіть перший від’ємний член арифметичної прогресії
7,2; 6,6; 6; ... .
16.23.• Між числами –6 і 3 вставте п’ять таких чисел, щоб вони разом із даними числами утворювали арифметичну прогресію.
16.24.• Які чотири числа треба вставити між числами 4 і –5, щоб вони разом із даними числами утворювали арифметичну прогресію?
16.25.• Знайдіть перший член і різницю арифметичної прогресії (an), якщо:
1) a3 + a7 = 30 і a6 + a16 = 60;
2) a4 + a10 = 36 і a a5æ 11 = 340.
16.26.• Знайдіть перший член і різницю арифметичної прогресії (an), якщо:
1) a5 + a12 = 41 і a10 + a14 = 62;
2) a7 + a13 = –104 і a a2æ 6 = −240.
16.27.• У яких випадках для членів арифметичної прогресії виконується рівність a a1 4 = a22 ?
16.28.• Доведіть, що значення виразів (a + b)2, a2 + b2,
|
сторін опуклого чотирикутника (рис. 16.1), узяті в послідовності a, b, d і c, утворюють арифметичну прогресію, то в цей чотирикутник можна вписати коло? |
d Рис. 16.1 |
![]() (a – b)2 є послідовними членами арифметичної b прогресії.
(a – b)2 є послідовними членами арифметичної b прогресії.
16.29.• Чи є правильним твердження: якщо довжини a
16.30.• Величини кутів трикутника утворюють арифметичну прогресію. Яка градусна міра середнього за величиною кута трикутника?
16.31.• Чи є послідовність (an) арифметичною прогресією, якщо її задано формулою n-го члена:
1) an = –6n + 3; 2) an = 2n2 – n; 3) an = –2,8n; 4) an = ![]() n ? n+ 1
n ? n+ 1
У разі ствердної відповіді вкажіть перший член і різницю прогресії.
16.32.• Чи є послідовність (an) арифметичною прогресією, якщо її задано формулою n-го члена:
2n− 1 1
1) an = 6 + 7n; 2) an = ![]() ; 3) an =
; 3) an = ![]() + 2?
+ 2?
5 n
У разі ствердної відповіді вкажіть перший член і різницю прогресії.
16.33.• З арифметичної прогресії вилучили члени з непарними номерами. Чи утворюють члени, що залишилися, арифметичну прогресію?
16.34.• Дано дві нескінченні арифметичні прогресії. Якщо від кожного члена однієї прогресії відняти відповідний член другої, то чи буде утворена послідовність арифметичною прогресією?
16.35.• Якщо в арифметичній прогресії, різниця якої не дорівнює нулю, вилучити її члени, номери яких кратні 3, то чи буде утворена послідовність арифметичною прогресією?
16.36.• Кожний член арифметичної прогресії помножили на 4. Чи буде утворена послідовність арифметичною прогресією?
16.37.• Доведіть, що числа, які дорівнюють відповідно сумам кутів трикутника, чотирикутника, п’ятикутника й т. д., утворюють арифметичну прогресію.
16.38.• При якому значенні x значення виразів x2 – 4, 5x + 3 і 3x + 2 будуть послідовними членами арифметичної прогресії? Знайдіть члени цієї прогресії.
16.39.• При якому значенні y значення виразів y2 + 1, y2 + y і 8y – 10 будуть послідовними членами арифметичної прогресії? Знайдіть члени цієї прогресії.
16.40.•• При якому значенні y значення виразів y2 – 2y, 3y + 5, 4y + 13 і 2y2 – y + 25 будуть послідовними членами арифметичної прогресії? Знайдіть члени цієї прогресії.
16. 41.•• При якому значенні x значення виразів 3x + 4, 2x + 3, x2 і 2x2 + x будуть послідовними членами арифметичної прогресії? Знайдіть члени цієї прогресії.
16.42.* Доведіть, що коли числа a, b і c — три послідовних члени арифметичної прогресії, то:
1) a2 + 8bc = (2b + c)2;
2) ![]() (a b c+ + )3 = a b c2 ( + ) + b a c2 ( + ) + c a b2 ( + ).
(a b c+ + )3 = a b c2 ( + ) + b a c2 ( + ) + c a b2 ( + ).
16.43.* Доведіть, що коли додатні числа a, b і c — три послідовних члени арифметичної прогресії, то 1 + 1 = 2 .
16.44.* Доведіть, що коли значення виразів ![]() є b c+ a c+ a b+
є b c+ a c+ a b+
послідовними членами арифметичної прогресії, то значення виразів a2, b2 і c2 також є послідовними членами арифметичної прогресії.
![]()
16.45. Розв’яжіть систему рівнянь:
x2 − 3y2 = 46, x2 − 2y2 = −4, 1) x y+ = 6; 2) x2 + 2y2 = 12.
16.46. Яка з наведених нерівностей рівносильна нерівності –5x < 10: 1) 5x < –10; 2) 10x > –20; 3) 10x < –20; 4) 5x > 10?
16.47. Чому дорівнює найменший цілий розв’язок нерівності 3 (x – 1)2 – 3x (x – 5) > –40?
16.48. Спростіть вираз:
![]()
![]() 1) (2 6 − 2 54 + 6 96 )æ2 3; 2) (5 20 − 6 10 + 2 40 )æ3 5.
1) (2 6 − 2 54 + 6 96 )æ2 3; 2) (5 20 − 6 10 + 2 40 )æ3 5.
16.49. Доведіть, що коли всі цифри трицифрового числа однакові, то це число кратне 37.
16.50. Робітник мав за певний строк виготовити 216 деталей. Перші три дні він виконував установлену щоденну норму, а потім став робити щодня 8 деталей понад норму. За день до кінця строку було виготовлено 232 деталі. Скільки деталей мав щоденно виготовляти робітник за нормою?
16.51. (Задача Безу[7].) Дехто купив коня і через деякий час продав його за 24 пістолі. При продажу він втратив стільки відсотків, скільки коштував йому кінь. Питання: за яку суму він купив коня?
16.52. Упровадження нових технологій дало змогу зменшити час на виготовлення однієї деталі з 12 хв до 10 хв. На скільки відсотків буде виконуватися при цьому план, якщо норму часу не буде змінено?
 17. Сума n перших членів арифметичної прогресії
17. Сума n перших членів арифметичної прогресії
Розглянемо скінченну арифметичну прогресію a1, a2, a3, ...,
an – 2, an – 1, an.
Суму членів цієї прогресії позначимо Sn. Маємо:
Sn = a1 + a2 + a3 + ... + an – 2 + an – 1 + an. (*) Виведемо формулу для знаходження цієї суми.
Спочатку розглянемо задачу, розв’язання якої підкаже, як вивести шукану формулу.
Розглянемо арифметичну прогресію
1, 2, 3, ..., 98, 99, 100
і знайдемо суму її членів.
Запишемо шукану суму двома способами та додамо отримані рівності:
S100 = 1 + 2 + 3 + ... + 98 + 99 + 100
+ S100 = 100 + 99 + 98 + ... + 3 + 2 + 1
![]()
2S
100 = 101 + 101 + 101 +...+ 101 + 101 + 101
100 доданків
Маємо: 2S100 = 101æ100; S100 = 5050.
![]() Розповідають, що видатний німецький математик Карл Фрідріх Гаусс придумав таке розв’язання у віці 5 років.
Розповідають, що видатний німецький математик Карл Фрідріх Гаусс придумав таке розв’язання у віці 5 років.
Скористаємося описаним прийомом для знаходження суми (*).
Запишемо суму Sn двома способами. Спочатку запишемо суму, перший доданок якої дорівнює a1, а кожний наступний доданок отримано з попереднього додаванням різниці d. Потім запишемо суму, перший доданок якої дорівнює an, а кожний наступний доданок отримано з попереднього
|
відніманням різниці d. Маємо: |
Карл Фрідріх Гаусс (1777–1855) |
Sn = a1 + (a1 + d) + (a1 + 2d) + ... + (a1 + (n – 2) d) + (a1 + (n – 1) d),
Sn = an + (an – d) + (an – 2d) + ... + (an – (n – 2) d) + (an – (n – 1) d).
Додавши ці рівності, отримаємо:
2Sn = (a1 + an) + (a1 + an) + ... + (a1 + an) + (a1 + an).
Вираз, записаний у правій частині останньої рівності, є сумою n доданків, кожний з яких дорівнює a1 + an. Тоді 2Sn = (a1 + an) n, тобто
a a1 + næn
Sn =
2
Отриману рівність називають формулою суми n перших членів арифметичної прогресії.
Підставивши до цієї формули замість an вираз a1 + d (n – 1), отримаємо:
Sn = ![]() a1 +a1 +d n( − 1)æn. 2
a1 +a1 +d n( − 1)æn. 2
Звідси
|
|
Останньою формулою зручно користуватися тоді, коли задано перший член і різницю прогресії.
![]() Приклад 1 Знайдіть суму всіх трицифрових чисел, які кратні 6.
Приклад 1 Знайдіть суму всіх трицифрових чисел, які кратні 6.
Розв’язання. Дані числа утворюють арифметичну прогресію,
перший член якої a1 = 102, а різниця d = 6. Тоді an = 102 + 6 (n – 1) = = 6n + 96. Знайдемо кількість членів цієї прогресії. Оскільки an < 1000, то шукана кількість — це найбільший натуральний розв’язок нерівності 6n + 96 < 1000. Маємо: 6n < 904; n < 150![]() .
.
Отже, n = 150. Тепер знайдемо шукану суму:
S150 = ![]() æ150 = 82 350.
æ150 = 82 350.
Відповідь: 82 350. ◄
![]() Приклад 2 Сума сімдесяти п’яти перших членів арифметичної прогресії дорівнює 450. Знайдіть тридцять восьмий член прогресії. Розв’язання. Нехай перший член прогресії та її різниця дорівнюють a1 і d відповідно. Тоді можна записати:
Приклад 2 Сума сімдесяти п’яти перших членів арифметичної прогресії дорівнює 450. Знайдіть тридцять восьмий член прогресії. Розв’язання. Нехай перший член прогресії та її різниця дорівнюють a1 і d відповідно. Тоді можна записати:
S75 = ![]() 2a1 + 74dæ75 = 75 (a1 + 37d) = 450.
2a1 + 74dæ75 = 75 (a1 + 37d) = 450.
2
Оскільки a38 = a1 + 37d, то шуканий член дорівнює a38 = 450 : 75 = 6.
Відповідь: 6. ◄
1. Як знайти суму n перших членів арифметичної прогресії, якщо відомо її перший і останній члени?
2. ![]() Як знайти суму nперших членів арифметичної прогресії, якщо відомо її перший член і різницю?
Як знайти суму nперших членів арифметичної прогресії, якщо відомо її перший член і різницю?
![]()
17.1.° Чому дорівнює сума семи перших членів арифметичної прогресії (an), якщо a1 = 9 і a7 = 15?
17.2.° Чому дорівнює сума шести перших членів арифметичної прогресії (bn), якщо b1 = 19 і b6 = 14?
17.3.° Знайдіть суму дванадцяти перших членів арифметичної прогресії, у якої a1 = –6 і d = 4.
17.4.° Обчисліть суму двадцяти перших членів арифметичної прогресії –8, –6, –4, ... .
17.5.° Місця в секторі цирку розташовано так, що в першому ряду 6 місць, а в кожному наступному на 3 місця більше, ніж у попередньому. Скільки місць у секторі, якщо в ньому 16 рядів?
17.6.° Дмитро взяв у бібліотеці книжку. За перший день він прочитав 40 сторінок, а кожного наступного дня читав на 10 сторінок більше, ніж попереднього. Скільки сторінок у книжці, якщо Дмитро прочитав її за 7 днів?
17.7.° Арифметичну прогресію (an) задано формулою n-го члена an = –4n + 1. Знайдіть суму тридцяти двох перших членів прогресії.
17.8.° Арифметичну прогресію (cn) задано формулою n-го члена cn = 5n – 2. Знайдіть суму двадцяти шести перших членів прогресії.
17.9.• Знайдіть суму дванадцяти перших членів арифметичної прогресії (an), якщо:
1) a1 = 6, a9 = 22; 2) a6 = 49, a20 = 7.
17.10.• Чому дорівнює сума сорока перших членів арифметичної прогресії (xn), якщо x8 = –14, x30 = –3?
17.11.• Скільки ударів зробить годинник протягом доби, якщо він відбиває тільки кількість цілих годин від 1 до 12?
17.12.• Знайдіть суму двадцяти п’яти перших членів арифметичної прогресії (an), якщо a10 = 44, а різниця прогресії d = 4.
17.13.• Знайдіть суму двадцяти перших членів арифметичної прогресії (an), якщо a6 + a8 – a14 = –17 і a5 + a22 = 101.
17.14.• Знайдіть суму тридцяти трьох перших членів арифметичної прогресії (an), якщо a3 + a5 + a13 = 33 і a15 – a8 – a10 = –1.
17.15.• При будь-якому n суму n перших членів деякої арифметичної прогресії можна обчислити за формулою Sn = 3n2 + 5n. Знайдіть три перших члени цієї прогресії.
17.16.• При будь-якому n суму n перших членів деякої арифметичної прогресії можна обчислити за формулою Sn = 9n – 2n2. Знайдіть сьомий член цієї прогресії.
17.17.• (Стародавня єгипетська задача) Сто мір хліба треба розділити між п’ятьма людьми так, щоб другий отримав на стільки ж більше за першого, на скільки третій отримав більше за другого, четвертий більше за третього та п’ятий більше за четвертого. Окрім того, двоє перших повинні отримати в 7 разів менше, ніж троє останніх. Скільки треба дати кожному?
17.18.• Чому дорівнює сума n перших:
1) натуральних чисел; 2) непарних чисел?
17.19.• Чому дорівнює сума n перших парних чисел?
17.20.•• Яке натуральне число дорівнює сумі всіх попередніх йому натуральних чисел?
17.21.•• Знайдіть суму всіх від’ємних членів арифметичної прогресії –6,2; –5,9; –5,6; ... .
17.22.•• Знайдіть суму всіх додатних членів арифметичної прогресії 8,4; 7,8; 7,2; ... .
17.23.•• Знайдіть суму всіх натуральних чисел, які кратні 5 і не більші за 240.
17.24.•• Знайдіть суму всіх натуральних чисел, які кратні 4 і менші від 130.
17.25.•• Знайдіть суму всіх натуральних чисел, які кратні 12 і менші від 200.
17.26.•• Знайдіть суму всіх трицифрових чисел, які кратні 8.
17.27.•• Знайдіть суму всіх трицифрових чисел, які кратні 7.
17.28.•• Знайдіть різницю арифметичної прогресії, перший член якої дорівнює 8,5, а сума шістнадцяти перших членів становить 172.
17.29.•• Знайдіть перший член арифметичної прогресії, різниця якої дорівнює –4, а сума дев’яти перших членів становить –54.
17.30.•• Перший член арифметичної прогресії дорівнює –9, а різниця становить 6. Скільки треба взяти перших членів прогресії, щоб їхня сума дорівнювала 960?
17.31.•• Яку найменшу кількість послідовних непарних натуральних чисел, починаючи із числа 7, треба додати, щоб одержати суму, більшу за 315?
17.32.•• Чи може сума яких-небудь п’яти послідовних членів арифметичної прогресії 3, 7, 11, ... дорівнювати 135? У разі ствердної відповіді знайдіть ці члени.
17.33.•• Чи може сума яких-небудь чотирьох послідовних членів арифметичної прогресії 2, 8, 14, ... дорівнювати 176? У разі ствердної відповіді знайдіть ці члени.
17.34.•• Під час вільного падіння тіло за першу секунду проходить 4,9 м, а за кожну наступну — на 9,8 м більше, ніж за попередню, якщо не враховувати опір повітря. Знайдіть час падіння тіла з висоти 490 м (опором повітря знехтувати).
17.35.•• Сума непарних номерів сторінок книжки є непарним числом, яке більше за 400 і менше від 500. Скільки сторінок у книжці?
17.36.•• Знайдіть суму членів арифметичної прогресії з восьмого по двадцять шостий включно, якщо перший член прогресії дорівнює 24, а різниця прогресії дорівнює –8.
17.37.•• Знайдіть суму членів арифметичної прогресії (xn) з десятого по двадцять п’ятий включно, якщо x1 = –3 і x11 = 12.
17.38.•• Сума перших шести членів арифметичної прогресії дорівнює 39, а сума перших чотирнадцяти членів дорівнює –77. Знайдіть перший член і різницю прогресії.
17.39.•• Перший член арифметичної прогресії дорівнює 100, а сума шести перших членів у 5 разів більша за суму наступних шести членів. Чому дорівнює різниця прогресії?
17.40.•• Різниця арифметичної прогресії дорівнює 28, а сума п’яти перших членів у 4 рази менша від суми наступних шести членів. Чому дорівнює перший член прогресії?
17.41.•• Дванадцятий член арифметичної прогресії дорівнює 30. Знайдіть суму двадцяти трьох перших членів прогресії.
17.42.•• Знайдіть суму двадцяти перших членів арифметичної прогресії (an), якщо a5 + a10 + a12 + a15 = 50.
17.43.•• Розв’яжіть рівняння:
1) 7 + 13 + 19 + ... + (6n + 1) = 480, де n — натуральне число; 2) 5 + 8 + 11 + ... + x = 124, де x — натуральне число.
17.44.•• Розв’яжіть рівняння:
1) 11 + 19 + 27 + ... + (8n + 3) = 470, де n — натуральне число; 2) 1 + 5 + 9 + ... + x = 630, де x — натуральне число.
17.45.•• Знайдіть перший член і різницю арифметичної прогресії, у якої середнє арифметичне n перших членів при будь-якому n дорівнює їхній кількості.
17.46.•• (Задача Гіпсикла Александрійського[8]) Доведіть, що в арифметичній прогресії з парною кількістю членів, яка складається із цілих чисел, сума другої половини більша за суму першої половини на число, яке кратне квадрату половини кількості членів.
17.47.•• Доведіть, що коли сума n перших членів послідовності обчислюється за формулою Sn = n2 – 3n, то ця послідовність є арифметичною прогресією. Знайдіть перший член і різницю цієї прогресії.
17. 48.•• Знайдіть суму всіх двоцифрових чисел, які не діляться націло ні на 3, ні на 5.
![]()
17.49. Побудуйте графік функції:
1) y = x2 – 4x + 4; 2) y = 2x2 + 8x + 8.
Користуючись побудованим графіком, знайдіть область значень, проміжки зростання і спадання функції.
17.50. Обчисліть:
349 48 54æ117 125
1) ![]() 25 ; 2)
25 ; 2) ![]() 4 ; 3)
4 ; 3) ![]() 6 ; 4)
6 ; 4) ![]() 3 .
3 .
9 8 55 18
17.51. При якому значенні k графіки функцій y = kx – 3 і y = x2 перетинаються в точці, абсциса якої дорівнює –2?
17.52. Спростіть вираз:
![]() d− 49 4 d + 24
d− 49 4 d + 24
1) ![]() ; 2) æ .
; 2) æ .
d+ 12 d + 36 3 d + 21
17.53. Велосипедист щохвилини проїжджає на 600 м менше, ніж мотоцикліст, тому на шлях 120 км він витрачає на 3 год більше за мотоцикліста. Знайдіть швидкість велосипедиста.
17.54. Одна вишивальниця може вишити набір серветок за 6 год, а друга — за 4 год. Якщо ж вони працюватимуть разом, то продуктивність праці кожної з них підвищиться на 20 %. За який час вони вишиють цей набір, працюючи разом?
17.55. Змішали 30-відсотковий розчин соляної кислоти з 10-відсотковим розчином і отримали 800 г 15-відсоткового розчину. Скільки грамів кожного розчину взяли для цього?
 УЧиМоСЯ Робити неСтандаРтні кРоки
УЧиМоСЯ Робити неСтандаРтні кРоки
17.56. Знайдіть усі пари чисел (x; y), які задовольняють рівняння

Розглянемо послідовності:
1, 3, 9, 27, 81, 243, ...,
1 1 1 1
![]() 2, 1, , , , , ...,
2, 1, , , , , ...,
2 4 8 16
5; –0,5; 0,05; –0,005; 0,0005; ... .
Їм притаманна така характерна особливість: кожний наступний член послідовності отримано в результаті множення попереднього члена на одне й те саме число. Для першої послідовності це число дорівнює 3, для другої це число дорівнює ![]() , для третьої це число дорівнює –0,1.
, для третьої це число дорівнює –0,1.
З подібними послідовностями можна зустрітися, наприклад, під час вивчення зростання колонії бактерій, при щомісячній оцінці суми грошей на рахунку, що покладені в банк під відсотки. Такі послідовності називають геометричними прогресіями.
Означення. Геометричною прогресією називають послідовність із відмінним від нуля першим членом, кожний член якої, починаючи з другого, дорівнює попередньому члену, помноженому на одне й те саме відмінне від нуля число.
Число, що дорівнює відношенню наступного і попереднього членів послідовності, називають знаменником геометричної прогресії та позначають буквою q (першою буквою французького слова quotient — частка).
Отже, якщо (bn) — геометрична прогресія зі знаменником q, то
b2 b3 b4 ..., q = = = = b1 b2 b3
bn+1 тобто для будь-якого натурального n виконується рівність ![]() = q.
= q.
bn Звідси отримуємо рекурентну формулу bn + 1 = bnq.
Таким чином, геометричну прогресію можна задати реку- рентно:
b1 = b, bn + 1 = bnq
Отже, щоб задати геометричну прогресію, потрібно вказати її перший член і знаменник.
Наведемо кілька прикладів.
Якщо b1 = 1 і q = 3, то отримаємо геометричну прогресію, подану на початку пункту:
1, 3, 9, 27, 81, 243, ... .
Якщо b1 = 2 і q = 2, то отримаємо геометричну прогресію, яка є послідовністю натуральних степенів числа 2:
2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, ... .
Зауважимо, що геометрична прогресія зі знаменником, який дорівнює 1, є послідовністю, усі члени якої рівні. Так, послідовність 5, 5, 5, 5, ... є геометричною прогресією, у якої b1 = 5, q = 1. Разом із цим цю послідовність можна розглядати як арифметичну прогресію, у якої a1 = 5, d = 0.
Узагалі, будь-яка послідовність, усі члени якої рівні між собою та відмінні від нуля, є одночасно і геометричною, і арифметичною прогресією. Послідовність 0, 0, 0, 0, ..., усі члени якої дорівнюють нулю, є лише арифметичною прогресією.
Покажемо, як можна задати геометричну прогресію за допомогою формули n-го члена.
З означення геометричної прогресії випливає:
b2 = b q1æ ;
b3 = b q2æ = (bq q bq1 )æ = 1 2; b4 = b q3æ = (bq1 2)æq bq= 1 3;
b5 = b q4æ = (bq1 3)æq bq= 1 4.
Ці приклади допомагають помітити таку закономірність: щоб знайти деякий член геометричної прогресії, можна перший член помножити на степінь з основою q і показником, який на 1 менший від номера шуканого члена. Звідси, наприклад, b6 = b1q5, b7 = b1q6, і взагалі
bn = b1qn – 1
Записану рівність називають формулою nго члена геометричної прогресії.
Установимо важливу властивість членів геометричної прогре- сії (bn).
Маємо:
b2 = b3 , звідси b22 = b b1æ 3; b1 b2
b3 = b4 , звідси b32 = b b2æ 4. b2 b3
![]() Узагалі, для будь-якого натурального n, більшого за 1, можна записати: bn = bn+1 . Звідси bn−1 bn
Узагалі, для будь-якого натурального n, більшого за 1, можна записати: bn = bn+1 . Звідси bn−1 bn
bn2 = bn−1æbn+1
Квадрат будь-якого члена геометричної прогресії, крім першого (і останнього, якщо прогресія є скінченною), дорівнює добутку двох сусідніх із ним членів.
Якщо всі члени геометричної прогресії (bn) є додатними, то рів-
ність bn2 = bn−1æbn+1 можна переписати так:
![]() bn = bn−1æbn+1 .
bn = bn−1æbn+1 .
Отже, кожний член такої послідовності, крім першого (і останнього, якщо послідовність є скінченною), є середнім геометричним двох сусідніх із ним членів.
Розглянемо дві послідовності.
Арифметична прогресія (an), у якої a1 = 1, d = 2:
1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, ... .
Геометрична прогресія (bn), у якої b1 = 1, q = 2:
1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, ... .
У цих прогресій перші члени є рівними. Обидві ці послідовності конструюються за допомогою одного й того самого числа 2 (d = q = 2). Разом з тим, порівнюючи відповідні члени цих послідовностей, ми бачимо, що геометрична прогресія «зростає» набагато швидше, ніж арифметична. Наприклад, в арифметичній прогресії a20 = 1 + 2æ19 = 39, у геометричній b20 = 1æ219 = 524 288.
Ви знаєте, що бактерії розмножуються поділом: одна бактерія ділиться на дві. Тепер стає зрозумілим, чому так швидко зростає чисельність бактерій, якщо їх помістити в сприятливе середовище.
Можливо, із цим прикладом пов’язано те, що нерідко в повсякденному житті, коли хочуть підкреслити швидке зростання якоїсь величини, кажуть: «зростає в геометричній прогресії».
![]() Приклад 1 У геометричній прогресії (bn) зі знаменником q =
Приклад 1 У геометричній прогресії (bn) зі знаменником q = ![]() знайдіть b1, якщо b6 =
знайдіть b1, якщо b6 = ![]() .
.
Розв’язання. Оскільки b6 = b1q5, то
![]() b1 = b q6 : 5 = 5 : 13 5 = 354æ35 = 5æ3 = 15.
b1 = b q6 : 5 = 5 : 13 5 = 354æ35 = 5æ3 = 15.
81 Відповідь: 15. ◄
![]() Приклад 2 Знайдіть четвертий член і знаменник геометричної прогресії (bn), якщо b3 = 36, b5 = 49.
Приклад 2 Знайдіть четвертий член і знаменник геометричної прогресії (bn), якщо b3 = 36, b5 = 49.
![]()
![]() Розв’язання. За властивістю геометричної прогресії b42 = b b3 5, звідси b4 = b b3 5 = 36æ49 = 6æ7 = 42 або b4 = − b b3 5 = −42.
Розв’язання. За властивістю геометричної прогресії b42 = b b3 5, звідси b4 = b b3 5 = 36æ49 = 6æ7 = 42 або b4 = − b b3 5 = −42.
Якщо b4 = 42, то знаменник прогресії q b b= 4 : 3 = ![]() = ; якщо b4 = –42, то q = −
= ; якщо b4 = –42, то q = −![]() .
.
Відповідь: b4 = 42, q = ![]() або b4 = –42, q = −
або b4 = –42, q = −![]() . ◄
. ◄
![]() Приклад 3 Знайдіть перший член і знаменник геометричної прогресії (bn), якщо b3 + b6 = 504 і b4 – b5 + b6 = 378.
Приклад 3 Знайдіть перший член і знаменник геометричної прогресії (bn), якщо b3 + b6 = 504 і b4 – b5 + b6 = 378.
Розв’язання. Нехай q — знаменник даної прогресії. Маємо систему двох рівнянь із двома змінними b1 і q:
bq1 2 + b1q5 = 504,
bq1 3 − bq1 4 + bq1 5 = 378.
Поділимо почленно ліві і праві частини рівнянь системи:
![]() b q13 2 (− +1 q q+q3 ) ) = 504378.
b q13 2 (− +1 q q+q3 ) ) = 504378.
2 b q1 (1 Далі отримуємо:
![]() b q1 2 (13+q) (− +q q1 − +q q) 2 ) = 43;
b q1 2 (13+q) (− +q q1 − +q q) 2 ) = 43;
2 b q1 (1
1 +q 4
= ;
q 3
4q = 3 + 3q; q = 3.
Підставивши значення q у перше рівняння системи, отримуємо:
9b1 + 243b1 = 504; звідси 252b1 = 504; b1 = 2. Відповідь: b1 = 2, q = 3. ◄
![]() Приклад 4 При якому значенні x значення виразів 3x, 7 – x і 5x + 7 будуть послідовними членами геометричної прогресії? Знай діть ці числа.
Приклад 4 При якому значенні x значення виразів 3x, 7 – x і 5x + 7 будуть послідовними членами геометричної прогресії? Знай діть ці числа.
Розв’язання. Якщо значення виразів 3x, 7 – x і 5x + 7 є послідовними членами геометричної прогресії, то має виконуватися рівність (7 – x)2 = 3x (5x + 7).
Далі отримуємо:
49 – 14x + x2 = 15x2 + 21x;
14x2 + 35x – 49 = 0; 2x2 + 5x – 7 = 0; x = 1 або x = −![]() .
.
Якщо x = 1, то отримуємо таку геометричну прогресію: 3, 6, 12. Якщо x = −![]() , то отримуємо таку геометричну прогресію: −
, то отримуємо таку геометричну прогресію: −![]() ,
,
![]() , −
, −![]() .
.
Відповідь: при x = 1 маємо: 3, 6, 12; при x = −![]() маємо: −
маємо: −![]() ,
,
![]() , −
, −![]() . ◄
. ◄
Розглянемо прикладну задачу, яку часто доводиться розв’язувати банківським працівникам, а також тим, хто зберігає гроші в банку під відсотки.
![]() Приклад 5 Нехай вкладник поклав у банк 100 000 грн під 10 % річних. Яка сума буде на його рахунку через 7 років за умови, що вкладник протягом цього строку не знімає гроші з рахунку?
Приклад 5 Нехай вкладник поклав у банк 100 000 грн під 10 % річних. Яка сума буде на його рахунку через 7 років за умови, що вкладник протягом цього строку не знімає гроші з рахунку?
Розв’язання. Нехай a0 — початковий капітал вкладника, тобто a0 = 100 000 грн.
Позначимо через a1, a2, ..., a7 кількість грошей на рахунку відповідно в кінці першого, другого, ..., сьомого років. Очевидно, що послідовність a0, a1, a2, ..., a7 є геометричною прогресією, знаменник якої дорівнює 110 %, тобто 1,1.
Тоді a7 = a0æ1 1, 7 = 100 000æ1 1, 7 = 194 871 71, (грн). Відповідь: 194 871,71 грн. ◄
Аналогічно розв’язують цю задачу в загальному вигляді, коли початковий капітал, який дорівнює a0, поклали в банк під p % річних. Тоді в кінці n-го року матимемо:
|
p n an = a0 1+ 100 |
Отриману формулу називають формулою складних відсотків.
1. Яку послідовність називають геометричною прогресією?
2. Яке число називають знаменником геометричної прогресії?
3. Який вигляд має формула n-го члена геометричної прогресії?
4. ![]() Як пов’язані між собою три послідовних члени геометричної прогресії?
Як пов’язані між собою три послідовних члени геометричної прогресії?
5. Який вигляд має формула складних відсотків? Поясніть її.
ВПРаВи
18.1.° Серед наведених послідовностей укажіть геометричні прогресії, перший член і знаменник кожної з них:
1) 2, 6, 18, 36; 4) 81, 27, 9, 3; 7) –9, –9, –9, –9;
2) 4, 8, 16, 32; 5) 2, –2, 2, –2; 8) 1, 2, 3, 5;
1 1
3) ![]()
![]()
![]() 10, 20, 30, 40; 6) − , , –1, 2; 9) 2, 2, 2 2, 4.
10, 20, 30, 40; 6) − , , –1, 2; 9) 2, 2, 2 2, 4.
4 2
18.2.° Шостий член геометричної прогресії (bn) дорівнює 8, а знаменник дорівнює –4. Знайдіть сьомий член прогресії.
18.3.° Знайдіть сьомий член геометричної прогресії (bn), якщо b8 = 16, а знаменник прогресії q = ![]() .
.
18.4.° Чому дорівнює знаменник геометричної прогресії (bn), якщо:
![]() 1) b1 = 6, b2 = –3; 2) b7 = –9, b8 = 15; 3) b10 = 3 3, b11 = 9?
1) b1 = 6, b2 = –3; 2) b7 = –9, b8 = 15; 3) b10 = 3 3, b11 = 9?
18.5.° Знайдіть знаменник геометричної прогресії (bn), якщо:
![]() 1) b12 = 24, b13 = 4; 2) b4 = − , b5 =
1) b12 = 24, b13 = 4; 2) b4 = − , b5 = ![]() 4 .
4 .
15
18.6.° Чому дорівнює перший член геометричної прогресії (bn), якщо b2 = 12, а знаменник прогресії q = ![]() ?
?
18.7.° Сьомий член геометричної прогресії дорівнює ![]() , а її знаменник дорівнює 4. Знайдіть шостий член прогресії.
, а її знаменник дорівнює 4. Знайдіть шостий член прогресії.
18.8.° Знайдіть чотири перших члени геометричної прогресії (xn), якщо x1 = 0,2, а знаменник прогресії q = –5.
18.9.° Перший член геометричної прогресії дорівнює −![]() , а знаменник дорівнює 3. Знайдіть п’ять перших членів прогресії.
, а знаменник дорівнює 3. Знайдіть п’ять перших членів прогресії.
18.10.° У геометричній прогресії (yn) перший член y1 = 64, а знаменник q = −![]() . Знайдіть: 1) y3; 2) y6; 3) y10.
. Знайдіть: 1) y3; 2) y6; 3) y10.
18.11.° У геометричній прогресії (cn) перший член c1 = 9, а знаменник q = –1. Знайдіть: 1) c21; 2) c50.
1
18.12.° Перший член геометричної прогресії b1 = ![]() , а її знаменник
, а її знаменник
125
q = 5. Знайдіть: 1) b4; 2) b7.
18.13.° Знайдіть знаменник і п’ятий член геометричної прогресії
1 1 1
![]() , , , ... .
, , , ... .
216 36 6
18.14.° Знайдіть знаменник і шостий член геометричної прогресії 18, 12, 8, ... .
18.15.° Доведіть, що коли послідовність (xn) — геометрична прогресія, то x3x13 = x5x11.
18.16.° Доведіть, що коли послідовність (yn) — геометрична прогресія, то y4y21 = y8y17.
18.17.° Вкладник поклав до банку 5000 грн під 8 % річних. Скільки грошей буде на його рахунку через три роки?
18.18.° Чотири роки тому завод виготовляв 10 000 одиниць певного виробу за рік. Завдяки модернізації виробництва та підвищенню продуктивності праці досягли щорічного приросту обсягів виробництва на 20 %. Скільки одиниць указаного виробу буде виготовлено цього року?
18.19.° Після двох послідовних знижень ціни на 10 % канцелярський стіл став коштувати 2916 грн. Знайдіть початкову ціну стола.
18.20.° Після двох послідовних підвищень ціни на 25 % люстра стала коштувати 937 грн 50 к. Знайдіть початкову ціну люстри.
18.21.° Населення міста за два роки збільшилося із 40 000 мешканців до 44 100. Знайдіть середній щорічний відсоток приросту населення в цьому місті.
18.22.° Унаслідок двох послідовних знижень ціни на одну й ту саму кількість відсотків ціна стільця знизилася з 800 грн до 578 грн. На скільки відсотків кожного разу знижували ціну?
18.23.• Виразіть члени b8, b13 і b60 геометричної прогресії (bn) через b7 і знаменник q.
18.24.• Виразіть члени c18, c36 і c50 геометричної прогресії (cn) через c12 і знаменник q.
18.25.• Знайдіть знаменник геометричної прогресії (bn), якщо:
1
1) b1 = ![]() , b8 = 64; 2) b6 = 75, b8 = 27.
, b8 = 64; 2) b6 = 75, b8 = 27.
2
18.26.• Знайдіть перший член геометричної прогресії (cn), якщо:
1) c4 = ![]() , а знаменник q =
, а знаменник q = ![]() ; 2) c6 = 100, c9 = 100 000.
; 2) c6 = 100, c9 = 100 000.
18. 27.• Число 486 є членом геометричної прогресії 2, 6, 18, ... . Знайдіть номер цього члена.
• 3 3 3
![]() 18.28. Число 96 є членом геометричної прогресії , , , ... .
18.28. Число 96 є членом геометричної прогресії , , , ... .
8 4 2
Знайдіть номер цього члена.
18.29.• Які два числа треба вставити між числами 6 і 750, щоб вони разом із даними числами утворили геометричну прогресію?
18.30.• Які чотири числа треба вставити між числами 0,5 і 16, щоб вони разом із даними числами утворили геометричну прогресію?
18.31.• Послідовність (bn) задано формулою n-го члена bn = 5æ4n−2. Чи є ця послідовність геометричною прогресією? У разі ствердної відповіді вкажіть її перший член і знаменник.
18.32.• Доведіть, що послідовність (xn), задана формулою n-го члена xn = 7n + 1, є геометричною прогресією, та вкажіть її перший член і знаменник.
18.33.• Послідовність (bn) є геометричною прогресією. Знайдіть:
1) b5, якщо b4 = 9, b6 = 25; 3) b17, якщо b16 = 2, b18 = 10.
2) b20, якщо b19 = –3, b21 = –12;
18.34.• При якому значенні змінної x числа x, 3x і 18 будуть послідовними членами геометричної прогресії?
18.35.• При якому значенні змінної y числа –1, 2y і –8 будуть послідовними членами геометричної прогресії?
18.36.• Другий член геометричної прогресії дорівнює 6. Знайдіть добуток трьох перших членів цієї прогресії.
18.37.• Третій член геометричної прогресії дорівнює 3. Знайдіть добуток п’яти перших членів цієї прогресії.
![]() 18.38.• Доведіть, що в скінченній геометричній прогресії добуток членів, рівновіддалених від її кінців, дорівнює добутку крайніх членів.
18.38.• Доведіть, що в скінченній геометричній прогресії добуток членів, рівновіддалених від її кінців, дорівнює добутку крайніх членів.
18.39.• У правильний трикутник зі стороною a послідовно вписано трикутники так, що вершини кожного наступного трикутника є серединами сторін попереднього (рис. 18.1). Доведіть, що периметри цих трикутників утворюють геометричну прогресію, і запишіть Рис. 18.1 формулу n-го члена цієї прогресії.
18.40.• Чи є геометричною прогресією послідовність:
1) 2–n, 2–2n, 2–3n, 2–4n; 3) 2n, 2n + 1, 2n + 2, 2n + 3?
2) 2n, 2n2 , 2n3 , 2n4 ;
У разі ствердної відповіді вкажіть знаменник прогресії.
18.41.• Послідовність (bn) є геометричною прогресією зі знаменником
q. Чи є геометричною прогресією послідовність:
1) b1, b3, ..., b2n – 1; 3) b1 + b2, b2 + b3, ..., bn – 1 + bn;
1 1 1
2) ![]() 2b1, 2b2, ..., 2bn; 4) , , ..., ?
2b1, 2b2, ..., 2bn; 4) , , ..., ?
b1 b2 bn
У разі ствердної відповіді вкажіть знаменник прогресії.
18.42.• Послідовність (bn) є геометричною прогресією зі знаменником
q. Чи є геометричною прогресією послідовність:
1) b2, b4, ..., b2n; 2) b1b3, b2b4, b3b5, ..., bn – 2bn?
У разі ствердної відповіді вкажіть знаменник прогресії.
18.43.•• Між числами 80 і 5 вставте три такі числа, щоб вони разом із даними числами утворювали геометричну прогресію.
18.44.•• Між числами 6 і 486 вставте три такі числа, щоб вони разом із даними числами утворювали геометричну прогресію.
18.45.•• Знайдіть перший член і знаменник геометричної прогресії (bn), якщо:
1) b5 = 3b3 і b6 – b2 = 48; 3) b5 – b4 = 168 і b3 + b4 = –28.
2) b4 + b7 = ![]() і b5 − b6 + b7 =
і b5 − b6 + b7 = ![]() ;
;
18.46.•• Знайдіть перший член і знаменник геометричної прогресії (bn), якщо:
1) b4 – b2 = 30 і b4 – b3 = 24;
2) b2 – b5 = 78 і b3 + b4 + b5 = –117.
18.47.•• При якому значенні x значення виразів 2x + 1, x + 5 і x + 11 будуть послідовними членами геометричної прогресії? Знайдіть члени цієї прогресії.
18.48.•• При якому значенні x значення виразів x + 6, x + 2 і 3x – 4 будуть послідовними членами геометричної прогресії? Знайдіть члени цієї прогресії.
18.49.•• Доведіть, що коли члени послідовності (bn) відмінні від нуля та при будь-якому натуральному n > 1 виконується рівність bn2 = bn−1æbn+1, то послідовність (bn) є геометричною прогресією.
18.50.•• Знайдіть геометричну прогресію, яка містить 6 членів, якщо сума трьох перших її членів дорівнює 168, а сума трьох останніх дорівнює 21.
18.51.•• Дано три додатних числа, які утворюють арифметичну прогресію. Їхня сума дорівнює 21. Якщо до цих чисел додати відповідно 2, 3 і 9, то отримані числа утворять геометричну прогресію. Знайдіть дані числа.
18.52.•• Дано три числа, які утворюють арифметичну прогресію. Їхня сума дорівнює 30. Якщо від першого числа відняти 5, від другого відняти 4, а третє залишити без змін, то отримані числа утворять геометричну прогресію. Знайдіть дані числа.
18.53.•• Дано три числа, які утворюють геометричну прогресію. Їхня сума дорівнює 65. Якщо від першого із цих чисел відняти 1, друге залишити без змін, а від третього відняти 19, то отримані числа утворять арифметичну прогресію. Знайдіть дані числа.
18. 54.•• Дано три числа, які утворюють геометричну прогресію. Їхня сума дорівнює 26. Якщо до цих чисел додати відповідно 1, 6 і 3, то отримані числа утворять арифметичну прогресію.
Знайдіть дані числа.
![]()
18.55. Знайдіть значення виразу:
79 1253 325 398
1) ![]() 10 ; 2)
10 ; 2) ![]() 4 ; 3)
4 ; 3) ![]() 4 ; 4)
4 ; 4) ![]() 10 7 .
10 7 .
7 25 64 3 æ13
|
18.56. Перетворіть у дріб вираз: |
|
|
|
2
x y+ x y− a− 4 |
a− 1
a− 6 |
c− 7 c− 3
|
18.58. Доведіть тотожність:
![]() 2b : 1 −b + 2 æb2 − 2b+ 1 : b− 1 = 1.
2b : 1 −b + 2 æb2 − 2b+ 1 : b− 1 = 1.
b3 + 1 b2 − +b 1 b− 1 4 b+ 1 2
18.59. Доведіть, що значення виразу є раціональним числом:
1) ![]()
![]() 10 − 10 ; 2) 2 − 5 + 2 + 5 .
10 − 10 ; 2) 2 − 5 + 2 + 5 .
10 + −9 3 10 + +9 3 2 + 5 2 − 5
18.60. Троє робітників викопали картоплю за 3 дні, працюючи щодня по 8 год. За скільки днів її викопають 6 робітників, працюючи щодня по 6 год, якщо продуктивність праці всіх робітників однакова?
18.61. До сплаву міді та цинку, який містив міді на 12 кг більше, ніж цинку, додали 6 кг міді. Унаслідок цього відсотковий вміст цинку в сплаві зменшився на 5 %. Скільки кілограмів цинку та скільки кілограмів міді містив сплав спочатку?
18.62. До сплаву магнію та алюмінію, який містив 12 кг алюмінію, додали 5 кг магнію, після чого відсотковий вміст магнію у сплаві збільшився на 20 %. Скільки кілограмів магнію було в сплаві спочатку?
18.63. Вкладник поклав у банк 4000 грн. За перший рік йому було нараховано певний відсоток річних, а другого року банківський відсоток було збільшено на 4 %. На кінець другого року на рахунку стало 4664 грн. Скільки відсотків становила банківська ставка в перший рік?
18.64. Вкладник поклав у банк 10 000 грн. За перший рік йому було нараховано певний відсоток річних, а другого року банківський відсоток було зменшено на 2 %. На кінець другого року на рахунку стало 11 880 грн. Скільки відсотків становила банківська ставка в перший рік?
![]() Як уникнути неоднозначності в задачах
Як уникнути неоднозначності в задачах
на відсоткові розрахунки
Задачі, у яких йдеться про зміну процентних ставок, можуть викликати певні ускладнення. Типовим прикладом є задачі 18.62, 18.63, у яких йдеться про збільшення (зменшення) «банківського відсотка». Відсоткова ставка — така сама величина, як і інші змінні величини — швидкість, відстань, ціна тощо. Єдина відмінність полягає в тому, що сама ця величина виражена також у відсотках. Тому ситуація, коли доводиться говорити про зміни цієї величини, припускає неоднозначне тлумачення. Порівняємо:
|
Підвищення ціни x |
Підвищення відсоткової ставки x |
Математична модель, що описує нове значення |
|
Ціна підвищилася на 10 грн |
Відсоткова ставка підвищилася на 10 % |
x + 10 |
|
Ціна підвищилася на 10 % |
Відсоткова ставка підвищилася на 10 % |
1,1x |
Бачимо, що у випадку відсоткової ставки словесний опис для різних математичних моделей виявився однаковим.
Щоб уникнути цієї неоднозначності, в економіці та інших областях, де широко застосовуються відсоткові розрахунки, використовують поняття «процентні пункти».
Наведемо характерний приклад.
У дев’ятих класах навчається 100 дітей, з яких 20 % на початок навчального року були відмінниками.
Якщо ми скажемо, що на кінець року кількість відмінників зросла на 5 %, то ця фраза означає, що кількість відмінників (виражена кількістю людей) збільшилася на 5 % від цієї величини. Кількість відмінників у цьому прикладі становила 20 осіб; коли ця кількість зросла на 5 %, то вже становила 21 особу.
Якщо ж ми хочемо сказати, що показник «20 %» збільшився й тепер дорівнює «25 %», то потрібно вживати слова «процентних пунктів»: «на кінець року кількість відмінників збільшилася на 5 процентних пунктів». За такого формулювання кількість відмінників на кінець року становитиме 25 осіб.
19. сума n перших членів геометричної прогресії
Тепер ми можемо переформулювати задачі так, щоб уникнути хибного тлумачення.
18.62. Вкладник поклав у банк 4000 грн. За перший рік йому було нараховано певний відсоток річних, а другого року банківський відсоток було збільшено на 4 процентних пункти. На кінець другого року на рахунку стало 4664 грн. Скільки відсотків становила банківська ставка в перший рік?
![]()
19. Сума n перших членів геометричної прогресії
Розглянемо скінченну геометричну прогресію b1, b2, b3, ..., bn – 1, bn. Суму членів цієї прогресії позначимо Sn. Маємо:
Sn = b1 + b2 + b3 + ... + bn – 1 + bn. (*)
Виведемо формулу для знаходження цієї суми.
Спочатку розглянемо задачу, розв’язання якої підкаже, як вивести шукану формулу.
Розглянемо геометричну прогресію 1, 2, 22, ..., 262, 263 і знайдемо суму її членів S64:
S64 = 1 + 2 + 22 + ... + 262 + 263.
Помножимо обидві частини записаної рівності на знаменник прогресії — число 2:
2S64 = 2 + 22 + ... + 262 + 263 + 264. Знайдемо різницю 2S64 – S64:
– 2SS6464 == 1 + 2 +2 + 2222 + 2+ 233 + ... + 2+ ... + 26363 + 264
![]()
2S64 – S64 = –1 + 0 + 0 + 0 + ... + 0 + 264
Звідси S64 = 264 – 1.
У вас може виникнути природне запитання: чому як приклад ми обрали саме прогресію 1, 2, 22, ..., 262, 263?
Із цією послідовністю пов’язана старовинна легенда. Індійський мудрець, який придумав гру в шахи, попросив за свій винахід у раджі скромну на перший погляд винагороду: за першу клітинку шахової дошки 1 пшеничне зернятко, за другу — 2, за третю — 4 і т. д. — за кожну наступну клітинку вдвічі більше зерняток, ніж за попередню.
Зрозуміло, що загальна кількість зерен, яку попросив винахідник, дорівнює S64 = 264 – 1.
Багатий раджа був приголомшений, коли дізнався, що він не в змозі задовольнити «скромне» бажання мудреця. Річ у тім, що значення виразу 264 – 1 дорівнює 18 446 744 073 709 551 615.
Щоб зрозуміти, наскільки величезним є це число, уявимо, що зерно зберігають у коморі площею 12 га. Тоді її висота була би більшою за відстань від Землі до Сонця.
Скористаємося описаним прийомом для знаходження суми (*). Перепишемо рівність (*) так:
Sn = b1 + b1q + b1q2 + b1q3 + ... + b1qn – 2 + b1qn – 1. Помножимо обидві частини цієї рівності на q:
Snq = b1q + b1q2 + b1q3 + b1q4 + ... + b1qn – 1 + b1qn. Знайдемо різницю Snq – Sn:
– Snq = b1q + b1q2 + b1q3 + ... + b1qn – 1 +b1qn Sn = b1 + b1q + b1q2 + b1q3 + ... + b1qn – 1
![]()
Snq – Sn = – b1 + 0 + 0 + 0 + ... + 0 +b1qn
Отже,
Snq – Sn = b1qn – b1.
Звідси Sn (q – 1) = b1 (qn – 1). При q ≠ 1 отримуємо:
|
b q( n −
q−1 |
Цю рівність називають формулою суми n перших членів геометричної прогресії зі знаменником, відмінним від 1.
Якщо q = 1, то всі члени прогресії дорівнюють першому члену. Тоді Sn = nb1.
![]() Приклад При будь-якому натуральному n сума n перших членів геометричної прогресії обчислюється за формулою Sn = 10 (2n – 1). Знайдіть перший член і знаменник цієї прогресії.
Приклад При будь-якому натуральному n сума n перших членів геометричної прогресії обчислюється за формулою Sn = 10 (2n – 1). Знайдіть перший член і знаменник цієї прогресії.
Розв’язання. Нехай b1 — перший член даної прогресії, q — її знаменник.
Тоді b1 = S1 = 10 (2 – 1) = 10; b1 + b2 = S2 = 10 (22 – 1) = 30. Звід-
b2 2. си b2 = 30 – b1 = 20; q = =
b1
Відповідь: b1 = 10, q = 2. ◄
19. сума n перших членів геометричної прогресії

19.1.° Знайдіть суму n перших членів геометричної прогресії (bn) зі знаменником q, якщо: 1) b1 = 10, q = 3, n = 4;
2) b1 = –4, q = –1, n = 10;
3) b1 = 0,6, q = 2, n = 5;
4) b1 = 4,5, q = ![]() , n = 8;
, n = 8;
5) ![]() b1 = –9, q = 3, n = 6;
b1 = –9, q = 3, n = 6;
6) b1 = 8, q = −![]() , n = 4.
, n = 4.
19.2.° Знайдіть суму n перших членів геометричної прогресії (bn) зі знаменником q, якщо: 1) b1 = 1, q = 2, n = 9;
2) b1 = 15, q = ![]() , n = 3;
, n = 3;
3) b1 = 18, q = −![]() , n = 5;
, n = 5;
4) ![]() b1 = 4, q = − 2, n = 4.
b1 = 4, q = − 2, n = 4.
19.3.° Знайдіть суму п’яти перших членів геометричної прогресії:
1 1 1
![]() 1) 12, 72, 432, ...; 2) , − , , ... .
1) 12, 72, 432, ...; 2) , − , , ... .
16 8 4
19.4.° Знайдіть суму чотирьох перших членів геометричної прогресії:
1) –0,6; 3; –15; ...; 2) 56; 42; 31,5; ... .
19.5.• Знайдіть суму шести перших членів геометричної прогресії (cn), якщо:
1) c4 = 216, а знаменник прогресії q = –3;
2) ![]()
![]() c1 = 5 5, c5 = 125 5, а знаменник прогресії q > 0.
c1 = 5 5, c5 = 125 5, а знаменник прогресії q > 0.
19.6.• Знайдіть суму семи перших членів геометричної прогресії (xn), якщо x3 = 24, x8 = 768.
19.7.• Геометричну прогресію (bn) задано формулою n-го члена bn = 10æ3n−1. Знайдіть суму п’яти перших членів прогресії.
19.8.• Геометричну прогресію (yn) задано формулою n-го члена
(−2)n+1
yn = ![]() . Знайдіть суму десяти перших членів прогресії. 20
. Знайдіть суму десяти перших членів прогресії. 20
19.9.• Знаменник геометричної прогресії дорівнює ![]() , а сума чотирьох перших членів дорівнює 65. Знайдіть перший член прогресії.
, а сума чотирьох перших членів дорівнює 65. Знайдіть перший член прогресії.
19.10.• Сума трьох перших членів геометричної прогресії дорівнює 516, а перший член дорівнює 12. Знайдіть знаменник прогресії.
19.11.• Сума членів скінченної геометричної прогресії дорівнює 605. Знайдіть кількість членів прогресії, якщо її перший член b1 = 5, а знаменник прогресії q = 3.
19.12.• Бактерія, потрапляючи в сприятливе середовище, наприкінці двадцятої хвилини ділиться на дві бактерії, кожна з яких наприкінці наступних 20 хв ділиться знову на дві й т. д. Скільки бактерій утворюється з однієї бактерії протягом доби?
19.13.• При будь-якому n сума перших n членів геометричної прогресії Sn = 4 (3n – 1). Знайдіть третій член цієї прогресії.
19.14.• При будь-якому n сума перших n членів геометричної прогресії Sn = 6 − ![]() 12 n − 1. Знайдіть четвертий член цієї прогресії.
12 n − 1. Знайдіть четвертий член цієї прогресії.
![]()
![]() 19.15.•• Знайдіть суму квадратів шести перших членів геометричної прогресії, перший член якої дорівнює 2 3, а знаменник дорівнює 3.
19.15.•• Знайдіть суму квадратів шести перших членів геометричної прогресії, перший член якої дорівнює 2 3, а знаменник дорівнює 3.
19.16.•• Знайдіть суму кубів чотирьох перших членів геометричної прогресії (bn), якщо b1 = 3 і b2 = –6.
19.17.•• Доведіть тотожність an – 1 = (a – 1) (an – 1 + an – 2 + ... + a + 1).
19. 18.•• Доведіть тотожність a2n + 1 + 1 = (a + 1) (a2n – a2n – 1 + ... + a2 – a + 1).
19. Геометрична прогресія
19.19.* Знайдіть кількість членів скінченної геометричної прогресії, знаменник якої q = 3, останній член cn = 162, а сума всіх членів Sn = 242.
![]()
19.20. Розв’яжіть систему нерівностей:
(x + 2) (x − 6) m (x + 2) (x + 1) + 4, 1) 2 6( x − 1) l7 (2x − 4);
![]() x− 1 − x− 2 l x− 3 − x,
x− 1 − x− 2 l x− 3 − x,
2) 2 3 4
1 − x > 0 5, x − 5.
19.21. Знайдіть проміжок зростання функції:
1) f (x) = 0,5x2 – 3x + 4; 2) f (x) = –3x2 – 2x + 4.
19.22. Побудуйте графік функції:
1) ![]() y = − + 3; 3) y = −
y = − + 3; 3) y = − ![]() 6 + 3.
6 + 3.
x+ 3
2) y = −;
x+ 3
19.23. За перший день двоє робітників виготовили 90 деталей. За другий день перший робітник виготовив деталей на 10 % більше, а другий — на 15 % більше, ніж за перший день. Усього за другий день вони виготовили 101 деталь. Скільки деталей виготовив кожний із них за перший день?
19.24. Спростіть вираз:
1) ![]() (a b− )2 + 16a2 , якщо a < 0 і b > 0;
(a b− )2 + 16a2 , якщо a < 0 і b > 0;
2) (x y− )2 − 9y2 , якщо x > 0 і y < 0.
19.25. Костюм коштував 600 грн. Після того як ціну було знижено двічі, він став коштувати 432 грн, причому відсоток зниження другого разу був у 2 рази більший, ніж першого. На скільки відсотків кожного разу знижувалася ціна?
19.26. Певний товар коштував 200 грн. Спочатку його ціну підвищили на кілька відсотків, а потім знизили на стільки ж відсот ків, після чого вартість його становила 192 грн. На скільки відсотків кожного разу відбувалася зміна ціни товару?
 УЧиМоСЯ Робити неСтандаРтні кРоки
УЧиМоСЯ Робити неСтандаРтні кРоки
19.27. На площині розташовано 100 точок. Відомо, що через кожні чотири з них проходить графік деякої квадратичної функції. Доведіть, що всі 100 точок належать графіку однієї квадратичної функції.
![]()
Разом з кожною послідовністю a1, a2, a3, ..., an, ... можна розглядати й таку послідовність (Sn):
S1 = a1, S2 = a1 + a2, S3 = a1 + a2 + a3, ..., Sn = a1 + a2 + ... + an, ... .
Знаходження формули n-го члена послідовності (Sn) називають сумуванням перших n членів послідовності (an).
Оскільки ви знаєте формули для обчислення суми n перших членів арифметичної і геометричної прогресій, то тим самим умієте сумувати перші n членів цих послідовностей.
За допомогою грецької літери S (сигма) суму a1 + a2 + ... + an
n
записують так: ∑ ak.
k=1
n
Наприклад, 12 + 22 + 32 + ... + n2 = ∑ k2;
k=1
n
13 + 23 + 33 + ... + n3 = ∑ k3.
k=1
Одним з ефективних способів сумування є використання раніше доведених формул.
n
![]()
![]() ПРикЛад 1 Знайдіть суму + + + ... +
ПРикЛад 1 Знайдіть суму + + + ... + ![]() 2 ænn + 1.
2 ænn + 1.
2
2kæk+ 1 1
![]() Розв’язання. Маємо: k = k + k .
Розв’язання. Маємо: k = k + k .
2 2
Тоді дану суму можна переписати так:
1 + ![]() 211 + 2 +
211 + 2 + ![]() 212 + 3 +
212 + 3 + ![]() 213 + ... + n +
213 + ... + n + ![]() 21n .
21n .
Звідси
1 + ![]() 11 +2 +
11 +2 + ![]() 212 +3 +
212 +3 + ![]() 213 + ... +n+
213 + ... +n+ ![]() 21n =
21n =
2
Сумування
![]()
![]() 2 2 2 2
2 2 2 2
![]() .
.
Отже, ![]()
![]() n . ◄ k=1 2 2 2
n . ◄ k=1 2 2 2
![]() Приклад 2 Знайдіть суму 7 + 77 + 777 + +... 77... 7.
Приклад 2 Знайдіть суму 7 + 77 + 777 + +... 77... 7.
n
Розв’язання. Оскільки 77 ...7= 7æ11...1, то для розв’язання
n n
задачі достатньо знайти суму Sn = 1 + 11 + 111 + ... + 11...1 і отрима-
n
ний результат помножити на 7. Маємо:
![]() 10 − 1 102 − 1 103 − 1
10 − 1 102 − 1 103 − 1
Sn = + + + ... +=
= ![]()
![]() 19 (1 + 1 + ... + 1) =
19 (1 + 1 + ... + 1) =
n
![]() = 1æ10 (10n − 1) − n = 10 (10n − 1) − n.
= 1æ10 (10n − 1) − n = 10 (10n − 1) − n.
9 10 − 1 9 81 9
70 (10n − 1) 7n
![]() Шукана сума дорівнює − . ◄
Шукана сума дорівнює − . ◄
81 9
Якщо для даної послідовності (an) вдається знайти таку послі-
n
довність (bn), що an = bn + 1 – bn, тоді суму ∑ ak знайти легко.
k=1
Справді, a1 + a2 + ... + an = (b2 – b1) + (b3 – b2) + (b4 – b3) + ... + + (bn + 1 – bn) = bn + 1 – b1.
![]() Приклад 3 Знайдіть суму 1 1æ ! + 2æ2! + 3æ3! + +... n næ !. Розв’язання. Маємо: n næ ! = (n + 1)! − n!.
Приклад 3 Знайдіть суму 1 1æ ! + 2æ2! + 3æ3! + +... n næ !. Розв’язання. Маємо: n næ ! = (n + 1)! − n!.
Тепер можна записати:
n
∑ k kæ ! = (2! − 1!) + (3! − 2!) + (4! − 3!) + ... + ((n + 1)! − n!) = (n + 1)! − 1. ◄
k=1
![]() ПРикЛад 4 Доведіть, що коли послідовність (an) — арифметична прогресія з ненульовими членами, то
ПРикЛад 4 Доведіть, що коли послідовність (an) — арифметична прогресія з ненульовими членами, то
1 1 1 n
![]() + + ... + = .
+ + ... + = .
a a1 2 a a2 3 a an n+1 a a1 n+1
![]() Розв’язання. Маємо: a a1 = a1n − an1+1 æd1 , де d — різниця
Розв’язання. Маємо: a a1 = a1n − an1+1 æd1 , де d — різниця
n n+1
прогресії. Тоді
![]()
![]() a a1 21 + a a2 31 + ... + a an n1 +1 = a11 − a12 ⋅ d1 + a12 − a13 ⋅ d1 + + 1 − 1 æd1 =
a a1 21 + a a2 31 + ... + a an n1 +1 = a11 − a12 ⋅ d1 + a12 − a13 ⋅ d1 + + 1 − 1 æd1 =
... an an+1
![]() = 1 1 − a12 + a12 − a13 + ... + a1n − an1+1 = d a1 11 − an1+1 = d a 1
= 1 1 − a12 + a12 − a13 + ... + a1n − an1+1 = d a1 11 − an1+1 = d a 1
an+1 −a1 = a1 +dn a− 1 = n . ◄
= ![]()
![]() da a1æ n+1 da a1æ n+1 a a1 n+1
da a1æ n+1 da a1æ n+1 a a1 n+1
5 13 25 2n2 + 2n + 1
![]()
![]() ПРикЛад 5 Знайдіть суму + + + ... + .
ПРикЛад 5 Знайдіть суму + + + ... + .
1æ2 2æ3 3æ4 n n( + 1)
Розв’язання. Маємо:
2n2 + 2n+ 1 2n n( + 1) + 1 1 1 1
![]() = = 2 + = 2 + − .
= = 2 + = 2 + − . 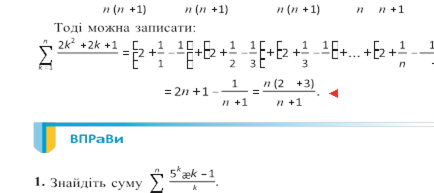 k k( + 1) 2 4
k k( + 1) 2 4
k=1 5
n 3k+1æk2 + 3kæk+ 1
2. ![]() Знайдіть суму ∑ k .
Знайдіть суму ∑ k .
k=1 3
3. Знайдіть суму:
1) 9 + 99 + 999 + ... + 99... 9;
n
2) 5 + 55 + 555 + ... + 55...5.
n
сумування
4. Доведіть, що коли послідовність (an) — арифметична прогресія з додатними членами, то
1 1 1 n
+ + ... + = .
![]()
5. Знайдіть суму:
1) ![]() ;
;
2) ![]() ... ;
... ;
1æ2 2æ3 3æ4 ( + 1)
3)
4) + + + ... + 2 2 .
4 36 144 n n( + 1)
6. Знайдіть суму:
1) ;
2) ![]()
![]() + + + ... + .
+ + + ... + .
n n( + 1) n 1
7. ![]() Знайдіть суму ∑ .
Знайдіть суму ∑ .
k=1
8. Знайдіть суму + .
1æ æ2 3 2æ æ3 4 n n( + 1) (n + 2)
9. Знайдіть суму Sn = 1 + 2a + 3a2 + 4a3 + ... + næan−1, де a ≠ 1.
ЗаВданнЯ № 4 «ПеРеВіРте Себе» В теСтоВій фоРМі
1. Серед поданих послідовностей укажіть арифметичну прогресію. А) 6, 9, 12, 13; В) 2, 8, 14, 21;
Б) 2, 9, 16, 23; Г) 2, 9, 16, 21.
2. Яка з поданих послідовностей є геометричною прогресією?
А) 3, 6, 9, 12; В) 3, 6, 12, 24;
Б) 3, 5, 7, 14; Г) 5, 8, 12, 16.
3. Чому дорівнює шостий член арифметичної прогресії, перший член якої дорівнює 12, а різниця дорівнює 0,4?
А) 14,4; Б) 14; В) 13,6; Г) 13.
4. Знайдіть різницю арифметичної прогресії (an), якщо a1 = –7, a2 = 5.
А) –2; Б) 2; В) –12; Г) 12.
5. Обчисліть суму десяти перших членів арифметичної прогресії, перший член якої a1 = –16, а різниця d = 3.
А) –10; Б) –15; В) –20; Г) –25.
6. Знайдіть четвертий член геометричної прогресії, перший член якої b1 = −![]() , а знаменник q = –2.
, а знаменник q = –2.
А) –2; Б) –1; В) 1; Г) 2.
7. Чому дорівнює знаменник геометричної прогресії (bn), якщо b1 = 36, b2 = 9?
А) ![]() ; Б) 4; В) 27; Г) –27.
; Б) 4; В) 27; Г) –27.
8. Обчисліть суму чотирьох перших членів геометричної прогресії, перший член якої b1 = 2, а знаменник q = 3.
А) 56; Б) 80; В) 96; Г) 192.
9. Знайдіть суму п’ятнадцяти перших членів арифметичної прогресії (an), заданої формулою n-го члена an = –4n + 13.
А) –300; Б) –285; В) –275; Г) –250.
10. Який номер члена арифметичної прогресії (an), що дорівнює 6,2, якщо a1 = 0,2, а різниця d = 0,4?
А) 14; Б) 15; В) 16; Г) 17.
11. Скільки додатних членів містить арифметична прогресія (an), якщо a1 = 41 і a2 = 38?
А) 13; Б) 14; В) 15; Г) 16.
Завдання № 4 «Перевірте себе» в тестовій формі
12. Знайдіть різницю арифметичної прогресії (an), якщо a1 + a5 = 28 і a2 + a3 = 24.
А) 4; Б) 3; В) 2,5; Г) 2.
13. Вкладник поклав у банк 4000 грн під 10 % річних. Скільки грошей буде на його рахунку через 2 роки?
А) 4840 грн; Б) 4800 грн; В) 4080 грн; Г) 4440 грн.
14. Шафа коштувала 15 000 грн. Після двох послідовних знижень її ціни на одну й ту саму кількість відсотків вона стала коштувати 9600 грн. На скільки відсотків щоразу знижували ціну?
А) 25 %; Б) 10 %; В) 15 %; Г) 20 %.
15. Знайдіть суму всіх натуральних чисел, які кратні 9 і менші від 120.
А) 810; Б) 702; В) 819; Г) 882.
16. Чому дорівнює сума дев’яти перших членів арифметичної прогресії (an), якщо a1 + a4 + a10 = 18?
А) 48; В) 72;
Б) 54; Г) знайти неможливо.
17. При якому значенні x значення виразів 7x – 8, 2x + 1 і x + 6 є послідовними членами арифметичної прогресії?
А) 1; В) –1;
Б) 2; Г) такого значення не існує.
18. При якому додатному значенні x значення виразів x + 1, 3x – 1 і 2x + 10 є послідовними членами геометричної прогресії?
А) 1,5; В) 3;
Б) 4; Г) такого значення не існує.
 ! гоЛоВне В ПаРагРафі 3
! гоЛоВне В ПаРагРафі 3
Послідовність
Об’єкти, які пронумеровано поспіль натуральними числами 1, 2, 3, ..., n, ..., утворюють послідовності.
Арифметична прогресія
Послідовність, кожний член якої, починаючи з другого, дорівнює попередньому члену, до якого додано одне й те саме число, називають арифметичною прогресією.
Формула nго члена арифметичної прогресії
an = a1 + d (n – 1)
Властивість членів арифметичної прогресії
Будь-який член арифметичної прогресії, крім першого (і останнього, якщо прогресія є скінченною), дорівнює середньому арифметичному двох сусідніх із ним членів:
an−1 +an+1 an = ![]() .
.
2
Формули суми n перших членів арифметичної прогресії
Sn = a1 +anæn;
2
Sn = ![]() æn
æn
Геометрична прогресія
Геометричною прогресією називають послідовність із відмінним від нуля першим членом, кожний член якої, починаючи з другого, дорівнює попередньому члену, помноженому на одне й те саме відмінне від нуля число.
Головне в параграфі 3
Формула nго члена геометричної прогресії
bn = b1qn – 1
Властивість членів геометричної прогресії
Квадрат будь-якого члена геометричної прогресії, крім першого (і останнього, якщо прогресія є скінченною), дорівнює добутку двох сусідніх із ним членів:
bn2 = b bn−1 n+1.
Формула суми n перших членів геометричної прогресії
Sn = b q1 ( n − 1)
![]()
q− 1
 20. Вправи для повторення курсу алгебри 9 класу
20. Вправи для повторення курсу алгебри 9 класу
20.1. Запишіть у вигляді нерівності твердження:
1) a — додатне число;
2) b — від’ємне число;
3) модуль числа c — невід’ємне число;
4) модуль суми двох раціональних чисел a і b не більший за суму модулів цих чисел.
20.2. Доведіть нерівність:
1) 3a (a + 6) < (3a + 6) (a + 4);
2) (2b – 1) (3b + 2) < (3b – 1) (2b + 1);
3) 25m2 + n2 l10mn;
4) 2a2 – 4a + 5 > 0;
5) x2 + x + 1 > 0;
6) 4y2 − 12 l12y − 21;
7) a2 + b2 + 2 l 2 (a + b);
8) a2 + b2 + c2 + 3 l 2 (a b c+ + );
9) 2a2 + 5b2 + 2ab + 1 > 0;
10) x2 + y2 + 15 > 6x + 4y.
20.3. Доведіть, що є правильною нерівність:
1) a5 − 5 l 5a4 −a, якщо al 5;
2) b3 + b + 2 l 0, якщо bl −1;
3) c3 +cm3c2 + 3, якщо cm3.
20.4. Відомо, що a > 3. Порівняйте з нулем значення виразу:
|
1) 2a – 6; |
4) (a – 3) (2 – a); |
|
2) 15 – 5a; |
a − 2 5) ; |
a − 1
![]() 3) 2a – 4; 6) −4 .
3) 2a – 4; 6) −4 .
3 − a
20.5. Відомо, що b < 2. Порівняйте з нулем значення виразу: b − 3
1) 4b – 8; 3) ![]() .
.
(2 − b b) ( − 4)
2) (b – 2)2 (b – 3);
20.6. Доведіть, що коли a > b > 1, то a2b + b2 + a > ab2 + a2 + b.
20.7. Доведіть, що коли a < b < 2, то
a2b + 2b2 + 4a < ab2 + 2a2 + 4b.
20.8. Порівняйте з нулем число a, якщо:
1) 6a < 5a; 3) 9a > 4a;
2) –2a < 2a; 4) –37a > –3a.
20.9. Доведіть, що коли a > 7 і b > 3, то: 1) 4a + b > 31; 2) 10a + 3b > 75.
20.10. Доведіть, що коли a > 5 і b < –2, то: 1) 3a – b > 17; 2) 5b – 2a < –10.
20.11. Порівняйте, якщо можливо:
1) 4a + b і 12, якщо a > 2 і b > 5;
2) b – 2a і 0, якщо a > 4 і b < 6; 3) b – 3a і 1, якщо a < 6 і b < 0; 4) a – 5b і 1, якщо a < 12 і b > 2.
20.12. Додатні числа a, b, c і d такі, що a > b, d < b і c > a. Розташуй-
1 1 1 1
![]() те в порядку зростання числа , , і .
те в порядку зростання числа , , і .
a b c d
20.13. Відомо, що 5 < a < 8. Оцініть значення виразу:
1) 0,4a; 3) 2a + 1;
2) a – 3; 4) –3a + 2.
![]() 20.14. Відомо, що 3,1 < 10 < 3,2. Оцініть значення виразу:
20.14. Відомо, що 3,1 < 10 < 3,2. Оцініть значення виразу:
![]()
![]() 1) 2 10; 2) −4 10; 3) 3 10 − 5.
1) 2 10; 2) −4 10; 3) 3 10 − 5.
20.15. Відомо, що 3 < m < 4 і –3 < n < –2. Оцініть значення виразу:
1) 2m + 3n; 3) –5m + 4n; m 2) 0,2m – n; 4) m − ![]() . n
. n
20.16. Розв’яжіть нерівність:
4 − 3x
1) 16 − 4nl 8; 4) ![]() < 1;
< 1;
7 2) 10x > 13x + 6; 5) 3x + 4 < 5x – 4; 3) 6x + 3 > 5x – 2; 6) 4x – 7 > 7x – 6.
20.17. ![]() Знайдіть суму натуральних чисел, які належать області визначення функції y = 10 − 3x.
Знайдіть суму натуральних чисел, які належать області визначення функції y = 10 − 3x.
20.18. Дано функцію f (x) = 3x + 12. При яких значеннях аргументу функція набуває: 1) додатних значень;
2) від’ємних значень;
3) значень, які належать проміжку [–4; 7]?
20.19. Придумайте нерівність виду ax + b > 0, де x — змінна, a і b — деякі числа, множиною розв’язків якої є: 1) проміжок (−3; +×);
2) проміжок (−×; −1 6, ); 3) множина дійсних чисел; 4) порожня множина.
20.20. Знайдіть множину розв’язків нерівності:
1) (2x − 3)2 m (4x − 1) (x − 2) + 7;
2) (x − 2) (2 + x) l 2 − (x + 4) (1 − x);
![]() 1 −x
1 −x
3) + 3 < 3x −;
4) ![]() − 9 > 7 − 2x + 2x;
− 9 > 7 − 2x + 2x;
5) 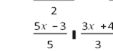 .
.
20.21. Чому дорівнює найменший цілий розв’язок нерівності
![]() x+ x− 2
x+ x− 2
− 1 m ![]() + x?
+ x?
3
20.22. Чому дорівнює найбільший цілий розв’язок нерівності
![]() 3x+ 5 < 8 −x ?
3x+ 5 < 8 −x ?
2 3
20.23. Чи є рівносильними нерівності:
1) ![]() x+ 1 + x− 1 < 1 і 3 (x + 1) + 2 (x – 1) < 1;
x+ 1 + x− 1 < 1 і 3 (x + 1) + 2 (x – 1) < 1;
2 3
2) (x + 3) (x2 + 4) > 0 і x + 3 > 0;
3) x – 1 > 3 і x − 1 + 1 > 3 + 1 ;
![]() x− 5 x− 5
x− 5 x− 5
4) x + 2 < 1 і x + 2 + 1 < 1 + 1 ? x x
20.24. Розв’яжіть систему нерівностей:
x − 3 < 2x − 3, (x − 5)2 − 15 l (x − 3) (x − 4) − 50,
1) 4x + 5 > 10 − x; 3) 4 (x + 7) − 16 l 2 − x;
x− 1
9 + 2xm3x + 7, 4 + x+31 7, l 3x5+ 1,
2) ![]() x − 2 > 2x − 5; 4) x+ 2 − x+ 8 < 3x− 1.
x − 2 > 2x − 5; 4) x+ 2 − x+ 8 < 3x− 1.
4 5 10
20.25. Знайдіть суму цілих розв’язків системи нерівностей:
3x − 5 < 23 − 4x,
1) 7x − 9 m 9x + 1;
2 3( x − 4) < 3 (4x − 5) + 23, 2) 4 (x + 1) m3x + 5.
20.26. Придумайте систему двох лінійних нерівностей з однією змінною, множиною розв’язків якої є:
1) проміжок (−2; +×);
2) проміжок −4; ![]() 13 ;
13 ;
3) проміжок (−×; −10];
4) порожня множина;
5) множина, яка складається з одного числа 8; 6) множина дійсних чисел.
20.27. Відомо, що 1 m ma 4. Скількох цілих значень може набувати вираз 0,5a – 3?
20.28. Розв’яжіть подвійну нерівність:
1) −3 m2x − 1 < 5; 3) 2 < 7 – 4x < 11;
2) −1 < 3x − 9 m6; 4) −2 m 1![]() − x m1.
− x m1.
3
20.29. При яких значеннях a має хоча б один розв’язок система нерівностей:
|
x < 4, 1) > ; x a |
xm−3, 3) l ; x a |
|
xm2, 2) > ; x a |
xl1, 4) m ? x a |
20.30. При яких значеннях a не має розв’язків система нерівностей:
x < 6, xm−8,
1) x a> ; 3) x al ;
xm5, x > 0,
2) x a> ; 4) x am ?
20.31. При яких значеннях a множиною розв’язків системи не-
xl 3, рівностей x a> є:
|
1) проміжок [7; +×); |
3) проміжок (−2; +×); |
|
2) проміжок [3; +×); |
4) порожня множина? |
20.32. При яких значеннях a рівняння x2 – (2a + 2) x – 2a – 3 = 0
має два різних від’ємних корені?
20.33. При яких значеннях a рівняння x2 – (2a – 1) x + a2 – a – 6 = 0
має два різних корені, які належать проміжку [–3; 2]?
20.34. На рисунку 20.1 зображено графік функції y = f (x), визначеної на множині дійсних чисел. Користуючись рисунком, укажіть:
1) нулі функції;
2) проміжки зростання і спадання функції; 3) множину розв’язків нерівності f (x) > 0.
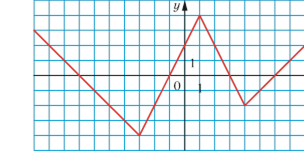
Рис. 20.1
20.35. На рисунку 20.2 зображено графік функції y = g (x), визначеної на проміжку [–5; 6]. Користуючись рисунком, укажіть:
1) область значень функції;
2) нулі функції;
3) проміжки зростання і спадання функції; 4) множину розв’язків нерівності g x( ) m 0.
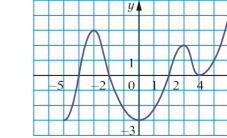
Рис. 20.2
20.36. Укажіть, які з наведених лінійних функцій є зростаючими, а які — спадними:
x
1) y = –4x; 3) y = ![]() ;
;
4
2) y = 4x – 7; 4) y = 4 – x.
20.37. Яка з наведених функцій є спадною:
1) y = x2; 3) y = –2x;
2
2) y = ![]() ; 4) y = 2x?
; 4) y = 2x?
x
20.38. Розв’яжіть графічно рівняння:
1) ![]() (x + 1)2 = − 2 ; 4) 6 = x + 3; x x− 2
(x + 1)2 = − 2 ; 4) 6 = x + 3; x x− 2
2) x2 − 2 = − x; 5) (x + 2)2 = x + 4;
3) ![]() x + 1 = 5 − x; 6)
x + 1 = 5 − x; 6) ![]() 5 + 3 = (x − 3) .2 x
5 + 3 = (x − 3) .2 x
20.39. Чому дорівнює абсциса вершини параболи:
1) y = 4x2 – 12x + 1; 2) y = –0,2x2 – 2x + 3?
20.40. Укажіть, вершина якої з даних парабол належить осі ординат, а якої — осі абсцис:
1) y = x2 – 4x + 3; 3) y = x2 – 6x + 9; 2) y = x2 – 8; 4) y = x2 + 2x.
20.41. Знайдіть значення b і c, при яких функція y = x2 + bx + c:
1) має єдиний нуль у точці x = –3;
2) набуває найменшого значення, що дорівнює 4, у точці x = 0; 3) має нулі в точках x = –2 і x = 5.
20.42. Побудуйте графік даної функції, знайдіть її область значень, проміжки зростання і спадання:
1) y = –2x2 + 1; 5) y = –x2 + 4x – 3; 2) y = 0,5x2 – 2; 6) y = x2 – 4x + 5;
3) y = x2 + 6x + 5; 7) y = 2x2 – 3x – 2;
4) y = 4x – x2; 8) y = –3x2 + 8x + 3.
20.43. При якому значенні c графік функції y = x2 – 6x + c:
1) проходить через початок координат;
2) має з віссю абсцис тільки одну спільну точку; 3) перетинає вісь ординат у точці A (0; –4); 4) перетинає вісь абсцис у точці B (2; 0)?
20.44. При якому значенні b графік функції y = x2 + bx + 2:
1) має з віссю абсцис тільки одну спільну точку;
2) не має з віссю абсцис спільних точок;
3) перетинає вісь абсцис у точках, відстань між якими дорівнює 4?
20.45. Графік функції y = x2 + px + q проходить через точки A (1; 1) і B (2; 2). Чи проходить цей графік через точку: 1) C (–1; –1); 2) D (3; 5)?
20.46. Парабола y = ax2 + bx + c проходить через точку (0; 10), а вершиною параболи є точка (6; –2). Знайдіть коефіцієнти a, b і c.
20.47. Значення квадратичної функції y = ax2 + bx + c у точці x = –1 дорівнює 0, а при x = ![]() функція набуває найменшого значення, яке дорівнює −
функція набуває найменшого значення, яке дорівнює −![]() . Знайдіть коефіцієнти a, b і c.
. Знайдіть коефіцієнти a, b і c.
20.48. При якому значенні m:
1) найменше значення функції y = x2 – 6x + m дорівнює –8; 2) найбільше значення функції y = –x2 + 4x – m дорівнює 12?
20.49. Побудуйте графік функції:
1) y = x3 + 4x2 − 5x; 3) y = xx42 −− 11;
![]()
![]() x4 − 13x2 + 36
x4 − 13x2 + 36
2) y =4) y = x2 − 9 .
20.50. При якому значенні a сума квадратів коренів рівняння x2 + ax + a – 2 = 0 набуватиме найменшого значення?
20.51. Відомо, що a + 3b = 10. Якого найменшого значення може набувати вираз a2 + b2 і при яких значеннях a і b?
20.52. Розв’яжіть нерівність:
1) x2 – 4x + 3 > 0; 5) –3x2 + 2x + 1 > 0;
2) x2 − 6x − 40 m 0; 6) x – x2 < 0;
3) x2 + x + 1l 0; 7) x2 + 25 l 0;
4) x2 – x + 1 < 0; 8) 0 1, x2 − 2 m 0.
20.53. Знайдіть цілі розв’язки нерівності:
1) ![]() x2 + 3x + 6 < 0; 2) −4x2 + 3x + 1l 0.
x2 + 3x + 6 < 0; 2) −4x2 + 3x + 1l 0.
20.54. При яких значеннях c тричлен 2x2 – 2x + 5c набуває додатного значення при будь-якому значенні x?
20.55. Розв’яжіть систему нерівностей:
x2 − 5x − 6 < 0, 6x2 + x − 2 > 0,
1) 5)
x > −1 2, ; x > 1;
x2 − 5x − 6 < 0, 6x2 + x − 2 > 0,
2) 6) 1
x > 0; x > − ![]() 3;
3;
x2 − 5x − 6 < 0, 6x2 + x − 2 > 0,
3) 7)
xl 6; x > −2;
x2 − 5x − 6 m 0, 6x2 + x − 2 l 0,
4) 8) 1 xl 6; xm ![]() 2.
2.
20.56. Розв’яжіть нерівність:
x2 − 16 x2 − 5x − 14
![]()
![]() 1) m 0; 2) l 0. x+ 1 x − 8
1) m 0; 2) l 0. x+ 1 x − 8
20.57. Знайдіть область визначення функції:
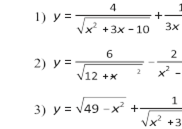
20.58. При яких значеннях a має два різних корені рівняння:
1) 2x2 + ax + a – 2 = 0;
2) (2a – 1) x2 + (a – 3) x + 1 = 0; 3) ax2 – (3a + 1) x + a = 0?
20.59. При яких значеннях a множиною розв’язків нерівності є множина дійсних чисел:
1) 5x2 – x + a > 0;
2) ax2 – 10x – 5 < 0;
3) ax2 − 2 (a − 1) x + 4am 0;
4) (a – 1) x2 – (a + 1) x + a + 1 > 0?
20.60. Розв’яжіть графічно систему рівнянь:
y x− 2 = 3, y x= 2 − 4,
1) 3) 2
x y+ = 5; y = −x + 4x − 4;
x y− = 7, x2 + y2 = 25,
2) xy = −12; 4) y x= 2 − 5.
20.61. Розв’яжіть систему рівнянь:
|
x − 4y = −6, 1) 2 2 x + 4y = 8; |
x2 − xy + y2 = 7, 6) x y− = 1; |
|
3x y+ = −2, 2) 2 3x − 2xy = 28; |
(x − 1) (y − 1) = −2, 7) + = 1; x y |
|
x + 2y = 13, 3) = 15; xy |
(x − 2) (y + 1) = 1, 8) − = 3; x y |
|
3x − 2y = 18, 4) = −12; xy |
9) x y 8 x y+ = 12; |
|
x2 − y2 = 21, |
|
|
|
|
5) 10) x y 5
x y+ = −3; y x− = 4.
20.62. Знайдіть розв’язки системи рівнянь:
|
x2 + y2 = 5, 1) xy = 2; |
2x2 − y2 = 14, 6) xy = −6; |
|
xy x+ + y = 11, 2) + = 30; xy x y( ) |
7) x y 10 xy = 50; |
|
x xy+ + y = 5, 3) − + = 1; x xy y |
8) y x 15 x2 − y2 = 16; |
|
x y− = 2,
y x 6 |
9) y x 12 x2 + y2 = 25; |
x2 + 2xy + y2 = 25, x2 + 2xy = 5,
5) 2 10) 2
x − 3xy = 4; y − 4xy = −4.
20.63. Знайдіть координати точок перетину:
1) прямої 3x – y – 5 = 0 і параболи y = ![]() x2 − 2x + 4;
x2 − 2x + 4;
2) прямої 2x – 3y – 3 = 0 і гіперболи xy = 3; 3) кола x2 + y2 = 13 і гіперболи xy = 6.
20.64. При якому значенні a має єдиний розв’язок система рівнянь:
x y− = 2, x2 + y2 = 6,
1) xy = a; 2) x y+ = a?
20.65. Діагональ прямокутника дорівнює 17 см, а його площа — 120 см2. Знайдіть сторони прямокутника.
20.66. Гіпотенуза прямокутного трикутника дорівнює 41 см, а його площа — 180 см2. Знайдіть катети трикутника.
20.67. Із двох міст, відстань між якими дорівнює 240 км, виїхали одночасно назустріч один одному два автомобілі. Через 2 год після початку руху відстань між автомобілями становила 40 км, причому зустріч автомобілів уже відбулася. Знайдіть швидкість кожного автомобіля, якщо весь шлях між містами один із них проїхав на годину швидше, ніж другий.
20.68. Із двох сіл, відстань між якими дорівнює 20 км, вирушили одночасно назустріч один одному два пішоходи, які зустрілися через 2 год. Знайдіть швидкість, з якою йшов кожний із них, якщо один пішохід долає відстань між селами на 1 год 40 хв швидше за другого.
20.69. Із пунктів A і B одночасно назустріч один одному вирушили відповідно велосипедистка і пішохід, які зустрілися через 1 год після початку руху. Знайдіть швидкість кожного з них, якщо велосипедистка прибула до пункту B на 2 год 40 хв раніше, ніж пішохід до пункту A, а відстань між цими пунктами становить 16 км.
20.70. Із міста A до міста B одночасно вирушили автобус і автомобіль. Через 1 год 30 хв після початку руху автомобіль випереджав автобус на 30 км. Коли автомобіль прибув у місто B, автобус знаходився на відстані 80 км від цього міста. Знайдіть швидкість автобуса і швидкість автомобіля, якщо відстань між містами A і B становить 300 км.
20.71. До басейну підведено дві труби. Якщо відкрити обидві труби, то басейн буде наповнено водою за 1,5 год, а якщо половину басейну наповнити через одну трубу, а решту після цього — через другу, то басейн буде наповнено за 4 год. За який час можна наповнити басейн через кожну трубу?
20.72. Двоє робітниць можуть виконати певне завдання за 9 год. Якби перша робітниця пропрацювала 1 год 12 хв, а потім друга — 2 год, то було б виконано 20 % завдання. За який час може виконати самостійно це завдання кожна робітниця?
20.73. Човен проходить 15 км за течією річки за той самий час, що й 12 км проти течії. Чому дорівнює швидкість течії, якщо 1 км за течією і 1 км проти течії човен проходить за 27 хв?
20.74. Велосипедист проїхав від села до залізничної станції по шосе завдовжки 10 км, а повернувся по ґрунтовій дорозі завдовжки 5 км, витративши на весь шлях 1 год 5 хв. Знайдіть швидкість руху велосипедиста по шосе та його швидкість руху по ґрунтовій дорозі, якщо на зворотний шлях він витратив на 15 хв менше, ніж на дорогу до станції.
20.75. Із міст A і B, відстань між якими дорівнює 180 км, виїхали одночасно назустріч один одному автобус і вантажівка. Після їхньої зустрічі автобус, який виїхав з міста A, прибув у місто B через 1 год, а вантажівка прибула в місто A через 2 год 15 хв. Знайдіть швидкість автобуса і швидкість вантажівки.
20.76. Послідовність (an) задано формулою n-го члена an = n2 – 4n + 4. Знайдіть шість перших членів цієї послідовності. Чи є членом цієї послідовності число: 1) 256; 2) 361; 3) 1000; 4) 10 000? У разі ствердної відповіді вкажіть номер цього члена.
20.77. Знайдіть кількість членів скінченної арифметичної прогресії (an), якщо a1 = 4, різниця прогресії d = –5, а останній член прогресії дорівнює –36.
20.78. Останній член арифметичної прогресії, яка містить 7 членів, дорівнює 3![]() . Знайдіть перший член цієї прогресії, якщо її різниця дорівнює
. Знайдіть перший член цієї прогресії, якщо її різниця дорівнює ![]() .
.
20.79. Який номер має перший від’ємний член арифметичної прогресії 2; 1,9; 1,8; 1,7; ...?
20.80. Які номери мають члени арифметичної прогресії 8, 11, 14, ..., які більші за 100, але менші від 200?
20.81. Сума скількох перших членів арифметичної прогресії 105, 98, 91, ... дорівнює нулю?
20.82. Знайдіть величини кутів опуклого чотирикутника, якщо вони утворюють арифметичну прогресію з різницею 54°.
20.83. Довжини сторін прямокутного трикутника утворюють арифметичну прогресію. Знайдіть катети трикутника, якщо його гіпотенуза дорівнює 4 см.
20.84. Відомо, що нескінченна послідовність a1, a2, a3, ... є арифметичною прогресією з різницею d ≠ 0. Чи є арифметичною прогресією послідовність:
1) –a2, –a4, –a6, –a8, ...;
2) a1 + 5, a2 + 5, a3 + 5, ...;
3) 1 – a1, 1 – a2, 1 – a3, ...;
4) a12, a22, a32, ...;
1 1 1
5) ![]() , , , ...; a1 a2 a3
, , , ...; a1 a2 a3
6) a1 + a2, a2 + a3, a3 + a4, ...;
7) a1 + a2, a3 + a4, a5 + a6, ...?
У разі ствердної відповіді вкажіть, чому дорівнює різниця прогресії.
20.85. Сума трьох чисел, які утворюють арифметичну прогресію, дорівнює 12, а сума їхніх квадратів дорівнює 80. Знайдіть ці числа.
20.86. Доведіть, що коли числа a, b і c є послідовними членами арифметичної прогресії, то значення виразів a2 + ab + b2, a2 + ac + c2, b2 + bc + c2 теж є послідовними членами деякої арифметичної прогресії.
20.87. Доведіть, що:
1) коли довжини a, b і c сторін трикутника утворюють арифметичну прогресію, то ac = 6Rr, де R і r — відповідно радіуси описаного та вписаного кіл трикутника;
2) коли довжини сторін прямокутного трикутника утворюють арифметичну прогресію, то її різниця дорівнює радіусу вписаного кола цього трикутника;
3) коли довжини сторін трикутника з кутом 120° утворюють арифметичну прогресію, то вони відносяться як 3 : 5 : 7.
20.88. Знайдіть суму n перших членів послідовності:
1) ![]() a − 1, a − 3, a − 5, ...; a a a
a − 1, a − 3, a − 5, ...; a a a
a b− 3a b− 5a b−
2) , , , ... . a b+ a b+ a b+
20.89. Третій член арифметичної прогресії дорівнює 11, а сьомий дорівнює 27. Скільки членів цієї прогресії потрібно взяти, щоб їхня сума дорівнювала 253?
20.90. Нехай Sn — сума n перших членів арифметичної прогресії (an). Знайдіть перший член і різницю прогресії, якщо:
1) a3 + a5 + a8 = 18 і a2 + a4 = –2;
2) a5 – a3 = –4 і a2a4 = –3;
3) a2 + a4 + a6 = 36 і a2a3 = 54; 4) S5 – S2 – a5 = 0,1 і a7 + S4 = 0,1; 5) S4 = 9 і S6 = 22,5.
20.91. Сума трьох перших членів скінченної арифметичної прогресії дорівнює 3, сума чотирьох перших членів дорівнює 16, а сума всіх членів дорівнює 220. Знайдіть кількість членів цієї прогресії.
20.92. Чому дорівнює сума сімнадцяти перших членів арифметичної прогресії, якщо її дев’ятий член дорівнює 15?
20.93. Довжини сторін прямокутного трикутника утворюють арифметичну прогресію, а його менший катет дорівнює a. Знайдіть площу трикутника.
20.94. Знайдіть суму двадцяти перших непарних чисел, при діленні яких на 3 остача дорівнює 1.
20.95. Чому дорівнює сума всіх двоцифрових чисел, які не діляться націло ні на 3, ні на 5?
20.96. Чи можуть довжини сторін прямокутного трикутника утворювати геометричну прогресію? У разі ствердної відповіді знайдіть знаменник цієї прогресії.
20.97. Після двох послідовних знижень ціни на одну й ту саму кількість відсотків ціна каструлі знизилася з 300 грн до 192 грн. На скільки відсотків знижували кожного разу ціну?
20.98. Дано геометричну прогресію (bn) зі знаменником q. Знайдіть: 1) b1, якщо b5 = −![]() , q = −
, q = −![]() ;
;
![]() 2
2
2) q, якщо b1 = ![]() , b4 = ;
, b4 = ;
3
3) суму семи перших членів прогресії, якщо b7 = 192, q = 2;
4) ![]() суму п’яти перших членів прогресії, якщо b5 = 9 6, q = 3.
суму п’яти перших членів прогресії, якщо b5 = 9 6, q = 3.
20.99. Сума трьох перших членів геометричної прогресії, яка містить 6 членів, у 8 разів менша від суми трьох останніх. Чому дорівнює знаменник прогресії?
20.100. Знайдіть 4 числа, які утворюють геометричну прогресію, якщо сума її крайніх членів дорівнює ![]() , а сума середніх дорівнює 10.
, а сума середніх дорівнює 10.
20.101. Відомо, що нескінченна послідовність b1, b2, b3, ... є геометричною прогресією зі знаменником q ≠ 1. Чи є геометричною прогресією послідовність:
1) b2, b4, b6, ...;
2) b1 + 1, b2 + 1, b3 + 1, ...;
3) b12, b22, b32, ...;
4) –b1, –b3, –b5, ...;
5) b1 + b2, b2 + b3, b3 + b4, ...;
1 1 1
6) ![]() , , , ...?
, , , ...?
b1 b2 b3
У разі ствердної відповіді вкажіть, чому дорівнює знаменник цієї прогресії.
для тих, хто хоче знати більше

Скількома способами учні вашого класу можуть стати один за одним у черзі до буфету? Скількома способами можна вибрати у вашому класі старосту та його заступника? Скількома способами можуть бути розподілені золоті, срібні та бронзові медалі на чемпіонаті світу з футболу?
Відповідаючи на ці запитання, потрібно підрахувати, скільки різних комбінацій, утворених за певним правилом, можна скласти з елементів заданої скінченної множини. Галузь математики, яка займається розв’язуванням подібних задач, називають комбінаторикою.
В основі розв’язування більшості комбінаторних задач лежать два правила: правило суми та правило добутку.
Розглянемо такий приклад. Туриста зацікавили 5 маршрутів по Наддніпрянщині та 7 маршрутів по Карпатах. З’ясуємо, скількома способами він може організувати свою відпустку, маючи час лише на один маршрут.
Оскільки всього є 5 + 7 = 12 різних маршрутів, то один із них можна вибрати 12 способами.
Узагальненням цього прикладу є таке правило.
Правило суми. Якщо множина A складається з m елементів, а множина B — з k елементів, причому ці множини не мають спільних елементів, то вибір «a або b», де a ∈A, b ∈B, можна здійснити m +k способами.
Правило суми можна узагальнити для трьох і більше множин. Наприклад, якщо множини A, B і C складаються відповідно з m, k і n елементів, причому жодні дві з цих множин не мають спільних елементів, то вибір «a або b або c», де a ∈ A, b ∈ B, c ∈ C, можна здійснити m + k + n способами.
Знову звернемося до прикладу з вибором маршрутів. Якщо турист має час на два маршрути та хоче побувати спочатку на Наддніпрянщині, а потім у Карпатах, то він може організувати свій відпочинок 35 способами. Справді, якщо вибрати один маршрут по Наддніпрянщині, то парою до нього може бути будь-який із
21. основні правила комбінаторики
7 карпатських маршрутів. Оскільки маршрутів по Наддніпрянщині 5, то кількість пар (маршрут по Наддніпрянщині; маршрут по Карпатах) дорівнює 7 + 7 + 7 + 7 + 7 = 7 . 5 = 35. Ці міркування ілюструє така таблиця:
|
|
|
Маршрути по Карпатах |
||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
||
|
Маршрути по Наддніпрянщині |
1 |
(1; 1) |
(1; 2) |
(1; 3) |
(1; 4) |
(1; 5) |
(1; 6) |
(1; 7) |
|
2 |
(2; 1) |
(2; 2) |
(2; 3) |
(2; 4) |
(2; 5) |
(2; 6) |
(2; 7) |
|
|
3 |
(3; 1) |
(3; 2) |
(3; 3) |
(3; 4) |
(3; 5) |
(3; 6) |
(3; 7) |
|
|
4 |
(4; 1) |
(4; 2) |
(4; 3) |
(4; 4) |
(4; 5) |
(4; 6) |
(4; 7) |
|
|
5 |
(5; 1) |
(5; 2) |
(5; 3) |
(5; 4) |
(5; 5) |
(5; 6) |
(5; 7) |
|
Узагальненням цього прикладу є таке правило.
Правило добутку. Якщо елемент a можна вибрати m способами і після кожного такого вибору елемент b можна вибрати k способами[9], то вибір «a і b» у вказаному порядку можна здійснити mk способами.
Правило добутку також природно узагальнити. Наприклад, якщо елемент a можна вибрати m способами, після кожного такого вибору елемент b можна вибрати k способами, і після того, як вибрано елементи a і b, елемент c можна вибрати n способами, то вибір «a і b і c» можна здійснити mkn способами.
![]() Приклад 1 Із класу, у якому навчаються 28 учнів, потрібно вибрати трьох чергових по одному на кожний із трьох поверхів школи. Скількома способами можна це зробити?
Приклад 1 Із класу, у якому навчаються 28 учнів, потрібно вибрати трьох чергових по одному на кожний із трьох поверхів школи. Скількома способами можна це зробити?
Розв’язання. Існує 28 способів вибрати чергового по першому поверху. Після того як цей вибір буде зроблено, залишиться 27 учнів, кожний з яких може стати черговим по другому поверху. Після вибору чергових для першого та другого поверхів чергового по третьому поверху можна вибрати 26 способами.
Таким чином, за правилом добутку кількість способів вибору трьох чергових дорівнює: 28 . 27 . 26 = 19 656.
Відповідь: 19 656 способами. ◄
Для тих, хто хоче знати більше
![]() Приклад 2 На рисунку 21.1 показано схему шляхів, що прокладено з міста A до міста B. Скількома способами можна проїхати з міста A до міста B?
Приклад 2 На рисунку 21.1 показано схему шляхів, що прокладено з міста A до міста B. Скількома способами можна проїхати з міста A до міста B?
![]() Розв’язання. Скориставшися правилом добутку, доходимо висновку, що
Розв’язання. Скориставшися правилом добутку, доходимо висновку, що
AB на дістатися 3з міста A до міста . 2 =B 6 через місто способами, а через M мож-
місто N — 4 . 3 = 12 способами. Тоді за правилом суми загальна кількість способів дорівнює: 6 + 12 = 18 способів.
Рис. 21.1 Відповідь: 18 способами. ◄

21.1.° Підніжжя гори та її вершину сполучають три стежки. Скільки є маршрутів від підніжжя до вершини й потім униз до підніжжя?
21.2.° Команді пропонують футболки трьох кольорів: червоного, зеленого та блакитного, а також труси двох кольорів — білого та жовтого. Скільки варіантів вибрати форму є в команди?
21.3.° Тетянка має п’ять суконь і три пари черевичків. Скільки варіантів вибрати вбрання є в Тетянки?
21.4.° У класі є 10 хлопчиків і 7 дівчинок. Скільки існує способів скласти пару для танців з одного хлопчика та однієї дівчинки?
21.5.°Скільки різних трицифрових чисел можна скласти із цифр:
1) 1 і 2; 2) 0 і 1
(цифри можуть повторюватися)?
21.6.° Із міста A до міста B проходять 4 шляхи, а з міста B до міста C проходять 3 шляхи (рис. 21.2). Скількома способами можна проїхати з міста A до міста C?

Рис. 21.2
21. Основні правила комбінаторики
21.7.° Кафе пропонує меню з 3 перших страв, 6 других страв і 5 третіх страв. Скільки є способів вибрати обід з трьох страв (по одній страві кожного виду)?
21.8.° Будемо розглядати склади з двох букв, перша з яких позначає приголосний звук, а друга — голосний. Скільки таких різних складів можна скласти з букв слова:
1) Полтава; 2) Миколаїв?
21.9.•Скільки чотирицифрових чисел, усі цифри яких різні, можна скласти із цифр 1, 2, 3, 4, якщо ці числа мають починатися: 1) із цифри 4; 2) із запису «23»?
21.10.• Скільки трицифрових чисел можна записати за допомогою цифр 0, 1, 2, 3, 4?
21.11.•Скільки існує двоцифрових чисел, усі цифри яких парні?
21.12.•Скільки існує двоцифрових чисел, усі цифри яких непарні?
21.13.•Монету підкидають 3 рази. Скільки різних послідовностей гербів і цифр можна отримати?
21.14.• Гральний кубик кидають 3 рази. Скільки різних послідовностей очок можна отримати?
21.15.•Кожну клітинку квадрата 2 × 2 можна пофарбувати в блакитний або червоний колір. Скільки існує способів пофарбувати цей квадрат?
21.16.•Скількома способами можна вибрати на шаховій дошці білу та чорну клітинки, які не лежать на одній і тій самій вертикалі та горизонталі?
21.17.••Скільки існує парних п’ятицифрових чисел?
21.18.••Скільки існує п’ятицифрових чисел, які кратні 10?
21.19.••Один колекціонер має для обміну 11 марок і 8 монет, другий — 9 марок і 7 монет. Скількома способами колекціонери можуть обміняти марку на марку або монету на монету?
21.20.••Скільки існує п’ятицифрових чисел, усі цифри яких мають однакову парність?
 22. Частота та ймовірність випадкової події
22. Частота та ймовірність випадкової події
Нам нерідко доводиться проводити спостереження, досліди, брати участь в експериментах або випробуваннях. Часто подібні дослідження завершуються деяким результатом, який заздалегідь передбачити неможливо.
Розглянемо кілька характерних прикладів.
• Якщо відкрити книгу навмання, то неможливо знати заздалегідь, який номер сторінки ви побачите.
• Неможливо до початку футбольного матчу визначити, з яким рахунком закінчиться гра.
• Ви не можете бути впевненим у тому, що коли натиснете на кнопку вимикача, то засвітиться настільна лампа.
• Немає гарантії, що з курячого яйця, покладеного до інкубатора, виведеться курча.
Як правило, спостереження або експеримент визначається якимось комплексом умов. Наприклад, футбольний матч повинен проходити за правилами; курячі яйця мають знаходитися в інкубаторі не менше ніж 21 день із дотриманням визначеної методики зміни температури та вологості повітря.
Результат спостереження, досліду, експерименту називають подією.
Випадковою подією називають такий результат спостереження або експерименту, який при дотриманні даного комплексу умов може відбутися, а може й не відбутися.
Наприклад, якщо кидати монету, то випадковою подією є випадіння герба. Виявлення листа при перевірці поштової скриньки також є випадковою подією.
Уявимо, що випущено 1 000 000 лотерейних білетів і розігрується один автомобіль. Чи можна, придбавши один лоте рейний білет, виграти цей приз? Звісно, можна, хоча ця подія малоймовірна. А якщо розігруватимуться 10 авто мобілів? Зрозуміло, що ймовірність виграшу збіль шиться. Якщо ж уявити, що розігруються 999 999 авто мобілів, то ймо вірність виграшу стає набагато більшою.
Отже, ймовірності випадкових подій можна порівнювати. Однак для цього слід домовитися, яким чином кількісно оцінювати можливість появи тієї чи іншої події.
Підставою для такої числової оцінки можуть бути результати численних спостережень або експериментів. Так, люди давно помітили, що багато подій відбувається з тією чи іншою, на подив постійною, частотою.
Демографам[10] добре відоме число 0,512. Статистичні дані, отримані в різні часи та в різних країнах, свідчать про те, що на 1000 новонароджених припадає в середньому 512 хлопчиків. Число 0,512 називають частотою випадкової події «народження хлопчика».
Воно визначається формулою
ʳëüê³ñòü íîâîíàðîäæåíèõ õëîï÷èê³â
×àñòîòà = .
ʳëüê³ñòü óñ³õ íîâîíàðîäæåíèõ
Наголосимо, що це число отримано в результаті аналізу багатьох спостережень. У таких випадках говорять, що ймовірність події «народження хлопчика» приблизно дорівнює 0,512.
![]() Ви знаєте, що куріння шкідливе для здоров’я. За даними організацій охорони здоров’я курці складають приблизно 92 % від усіх хворих на рак легенів. Число 0,92 — це частота випадкової події «той, хто захворів на рак легенів, — курив», яка визначається таким відношенням:
Ви знаєте, що куріння шкідливе для здоров’я. За даними організацій охорони здоров’я курці складають приблизно 92 % від усіх хворих на рак легенів. Число 0,92 — це частота випадкової події «той, хто захворів на рак легенів, — курив», яка визначається таким відношенням:
×àñòîòà = ʳëüê³ñòü êóðö³âñåðåäòèõ,õòîçàõâîð³âíà ðàêëåãåí³â. ʳëüê³ñòü óñ³õ ëþäåé, ÿê³çàõâîð³ëèíà ðàêëåãåí³â
У таких випадках говорять, що ймовірність натрапити на курця серед тих, хто захворів на рак легенів, приблизно дорівнює 0,92 (або 92 %).
Щоб детальніше ознайомитися з поняттям ймовірності випадкової події, звернемося до класичного прикладу з киданням монети.
Припустимо, що в результаті двох підкидань монети двічі випав герб. Тоді у даній серії, яка складається з двох випробувань, частота випадіння герба дорівнює:
×àñòîòà= ![]() ʳëüê³ñòü âèïàä³íü ãåðáà = =2 1. ʳëüê³ñòü êèäê³â 2
ʳëüê³ñòü âèïàä³íü ãåðáà = =2 1. ʳëüê³ñòü êèäê³â 2
Чи це означає, що ймовірність випадіння герба дорівнює 1?
Звісно, ні.
Для того щоб за частотою випадкової події можна було оцінювати її ймовірність, кількість випробувань має бути достатньо великою.
Починаючи з ХVІІІ ст. багато дослідників проводили серії випробувань із підкиданням монети.
У таблиці наведено результати деяких таких випробувань.
|
Дослідник |
Кількість підкидань монети |
Кількість випадінь герба |
Частота випадіння герба |
|
Жорж-Луї де Бюффон (1707–1788) |
4040 |
2048 |
0,5069 |
|
Аугустус де Морган (1806–1871) |
4092 |
2048 |
0,5005 |
|
Вільям Джевонс (1835–1882) |
20 480 |
10 379 |
0,5068 |
|
Всеволод Романовський (1879–1954) |
80 640 |
39 699 |
0,4923 |
|
Карл Пірсон (1857–1936) |
24 000 |
12 012 |
0,5005 |
|
Вільям Феллер (1906–1970) |
10 000 |
4979 |
0,4979 |
За наведеними даними простежується закономірність: при багаторазовому підкиданні монети частота появи герба незначно відхиляється від числа 0,5.
Отже, можна вважати, що ймовірність події «випадіння герба» приблизно дорівнює 0,5.
У кожному з розглянутих прикладів використовувалося поняття частота випадкової події. Цю величину ми обчислювали за формулою:
×àñòîòà= ʳëüê³ñòü ïîÿâ ïî䳿, ÿêà ö³êàâèòü .
![]()
ʳëüê³ñòü âèïðîáóâàíü (ñïîñòåðåæåíü)
Звернемося знову до таблиці, наведеної вище. Чи можна на основі її даних гарантовано стверджувати, що ймовірність випадкової події «випадіння герба» дорівнює числу 0,5? Відповідь на це запитання заперечна. Справді, на основі цих даних можна сказати, що частота появи герба незначно відхиляється від числа 0,502 або від числа 0,4997, тобто число 0,5 не має жодних переваг перед числом 0,502 або числом 0,4997.
Таким чином, частота випадкової події дає змогу лише наближено оцінити ймовірність випадкової події. Чим більше випробувань провести, тим точнішою буде оцінка ймовірності випадкової події за її частотою.
Таку оцінку ймовірності випадкової події називають статистичною. Її використовують у різних галузях діяльності людини: фізиці, хімії, біології, страховому бізнесі, соціології, економіці, охороні здоров’я, спорті тощо.
Ймовірність події позначають буквою P (першою буквою французького слова probabilité — ймовірність).
Якщо в першому прикладі подію «народження хлопчика» позначити буквою A, то отриманий результат записують так:
P (A) ≈ 0,512.
Ураховуючи наближений характер статистичної оцінки, отримані дані можна округлити. Наприклад, коли частота випадкової події дорівнює 0,512, то можна записати, що P (A) ≈ 0,51 або P (A) ≈ 0,5. Якщо подію «випадіння герба» позначити буквою B, то P (B) ≈ 0,5.
На закінчення цього пункту зазначимо таке. Нерідко в повсякденному житті ми приймаємо правильні й опти мальні рішення, використовуючи ймовірнісні властивості нав колишніх явищ або об’єктів. Наведемо кілька прикладів.
• Якщо ви хочете дізнатися, як розв’язувати задачу з домашнього завдання, то, скоріш за все, зателефонуєте однокласнику, який добре знає математику. Цей вибір базується на тому, що для сильного учня ймовірність розв’язати задачу більша, ніж для слабкого.
• Товари популярних фірм дорожчі за аналогічні товари маловідомих фірм. Проте нерідко ми купляємо дорожчий товар. Таке рішення багато в чому визначається тим, що ймовірність купити неякісний виріб у відомої фірми менша, ніж у маловідомої фірми.
• Нехай контрольна робота складається з десяти завдань у тестовій формі з вибором відповіді. Припустимо, що ви впоралися з дев’ятьма задачами, а десяту розв’язати не можете. Залишається лише одне — відповідь угадувати. Скоріш за все, ви не вибиратимете літеру, що позначає варіант відповіді, яка в попередніх де в’яти завданнях трапилася частіше за інші. Ці міркування ба зу ються на тому, що укладачі тестових завдань навряд чи розташували варіанти відповідей так, щоб якась літера, що позначає правильну відповідь, траплялася набагато частіше за інші.
Наголосимо, що окремо взятий вибір, який зроблено на основі ймовірнісної оцінки, може виявитися невдалим. Незважаючи на це, під час прийняття подальших аналогічних рішень не варто відкидати вибрану стратегію керуватися ймовірнісними характеристиками, оскільки такий підхід збільшує шанси на успіх.
1. Наведіть приклади випадкових подій.
2. опишіть, що таке частота випадкової події.
3. ![]() За яких умов частота випадкової події може оцінювати ймовірність випадкової події?
За яких умов частота випадкової події може оцінювати ймовірність випадкової події?
4. Як позначають ймовірність події A?
ВПРаВи
22.1.° Наведіть приклади випробувань, результатом яких, на вашу думку, є: 1) малоймовірна подія; 2) дуже ймовірна подія.
22.2.° Чи можна вважати малоймовірною подію:
1) при підкиданні монети 200 разів поспіль випав герб;
2) наступного тижня вас викличуть до дошки хоча б один раз;
3) у футбольному матчі «Шахтар» — «Динамо» (Київ) зафіксовано результат 1 : 1;
4) натискаючи навмання клавіші клавіатури комп’ютера, отримали слово «математика»?
![]() 22.3.° Експеримент полягає у підкиданні кнопки. Кнопка може впасти як вістрям донизу, так і на шляпку (рис. 22.1). Підкиньте кнопку: 1) 10 разів; 2) 20 разів; 3) 50 разів; 4) 100 разів; 5) 200 разів.
22.3.° Експеримент полягає у підкиданні кнопки. Кнопка може впасти як вістрям донизу, так і на шляпку (рис. 22.1). Підкиньте кнопку: 1) 10 разів; 2) 20 разів; 3) 50 разів; 4) 100 разів; 5) 200 разів.
Результати, отримані в п’яти серіях екс- Рис. 22.1 периментів, занесіть у таблицю.
|
Номер серії |
1 |
2 |
3 |
4 |
5 |
|
Кількість експериментів (підкидань) у серії |
10 |
20 |
50 |
100 |
200 |
|
Кількість випадінь кнопки вістрям униз |
|
|
|
|
|
|
Кількість випадінь кнопки вістрям догори |
|
|
|
|
|
У кожній із п’яти серій експериментів підрахуйте частоту випадіння кнопки вістрям догори й оцініть ймовірність настання цієї події. Яка подія більш ймовірна: «кнопка впаде вістрям униз» або «кнопка впаде вістрям догори»?
22.4.° Експеримент полягає в підкиданні двох монет. Проведіть цей експеримент: 1) 10 разів; 2) 20 разів; 3) 50 разів; 4) 150 разів. Результати, отримані в кожній із чотирьох серій експериментів, занесіть у таблицю.
|
Номер серії |
1 |
2 |
3 |
4 |
|
Кількість експериментів (підкидань) у серії |
10 |
20 |
50 |
150 |
|
Кількість експериментів, у яких випало два герби |
|
|
|
|
|
Кількість експериментів, у яких випав рівно один герб |
|
|
|
|
|
Кількість експериментів, у яких не випало жодного герба |
|
|
|
|
У кожній із чотирьох серій експериментів підрахуйте частоту випадкової події:
1) випадіння двох гербів;
2) випадіння тільки одного герба;3) випадіння двох чисел.
Чи можна на основі цих спостережень зробити припущення, що подія «випав рівно один герб» є більш ймовірною, ніж подія «не випало жодного герба»? На чому базується таке припущення? Чи можна на основі цих спостережень гарантувати, що перша з названих подій є більш ймовірною, ніж друга?
![]() 22.5.° Проведіть серію, яка складається зі 100 експериментів, у яких підкидають ґудзик з петлею (рис. 22.2). Знайдіть частоту події «ґудзик упаде петлею вниз». Оцініть ймовірність події «ґудзик
22.5.° Проведіть серію, яка складається зі 100 експериментів, у яких підкидають ґудзик з петлею (рис. 22.2). Знайдіть частоту події «ґудзик упаде петлею вниз». Оцініть ймовірність події «ґудзик
упаде петлею догори» у проведеній серії експе-
Рис. 22.2 риментів.
22.6.° У таблиці наведено дані про народження дітей у місті N за 2016 рік.
|
Місяць |
|
|
|
|
|
|
|
|
|
|
|
|
|
Кількість народжень хлопчиків |
1198 |
1053 |
1220 |
1151 |
1151 |
1279 |
1338 |
1347 |
1329 |
1287 |
1196 |
1243 |
|
Кількість народжень дівчаток |
1193 |
1065 |
1137 |
1063 |
1163 |
1228 |
1258 |
1335 |
1218 |
1239 |
1066 |
1120 |
Підрахуйте частоту народжень хлопчиків у кожному місяці та за весь 2016 рік. Оцініть ймовірність народження дівчинки у 2016 році.
22.7.° Оператор довідкової служби протягом робочого дня (9:00– 17:00) у середньому розмовляє по телефону 6 год. Оцініть ймовірність того, що коли зателефонувати до довідкової у цей період, телефон виявиться вільним.
22.8.° За статистикою у місті Одеса протягом літа кількість сонячних днів у середньому дорівнює 70. Оцініть ймовірність того, що, приїхавши влітку в Одесу на один день, гість натрапить на похмуру погоду.
22.9.° З великої партії лампочок вибрали 1000, серед яких виявилося 5 бракованих. Оцініть ймовірність купити браковану лампочку.
22.10.° Під час епідемії грипу серед обстежених 40 000 жителів виявили 7900 хворих. Оцініть ймовірність події «навмання вибрана людина хвора на грип».
22.11.° Ймовірність купити браковану батарейку дорівнює 0,02. Чи можна стверджувати, що в будь-якій партії зі 100 батарейок є дві браковані?
22.12.° Ймовірність влучити в мішень становить 85 %. Чи може бути так, що в серії зі 100 пострілів було 98 влучень у мішень?
22.13.• Наведену таблицю називають «Навчальний план 9 класу загальноосвітньої школи»:
|
Предмет |
Кількість годин на тиждень |
Предмет |
Кількість годин на тиждень |
|
Українська мова |
2 |
Геометрія |
2 |
|
Українська література |
2 |
Біологія |
2 |
|
Іноземна мова |
3 |
Географія |
2 |
|
Зарубіжна література |
2 |
Фізика |
3 |
|
Історія України |
2 |
Хімія |
2 |
|
Всесвітня історія |
1 |
Трудове навчання |
1 |
|
Правознавство |
1 |
Інформатика |
2 |
|
Мистецтво |
1 |
Основи здоров’я |
1 |
|
Алгебра |
2 |
Фізична культура |
3 |
Оцініть ймовірність того, що вибраний навмання урок у тижневому розкладі 9 класу виявиться: 1) алгеброю; 2) геометрією; 3) математикою; 4) фізкультурою; 5) іноземною мовою.
22.14.• Виберіть навмання одну сторінку з повісті Марка Вовчка «Інститутка». Підрахуйте, скільки разів на цій сторінці зустрінуться букви «н», «о», «я», «ю», а також скільки всього на ній букв. Оцініть ймовірність появи цих букв у вибраному тексті. Ця оцінка дозволить зрозуміти, чому на клавіатурах друкарської машинки та комп’ютера (рис. 22.3) букви «н» і «о» розміщено ближче до центру, а букви «я» і «ю» — ближче до краю.

Рис. 22.3
22.15.• У таблиці наведено дані про кількість днів 2016 року, у які на 12.00 було зафіксовано дану температуру та даний рівень вологості повітря в місті N.
|
Діапазон температури повітря, °С |
Діапазон вологості повітря, % |
|
|
||||
|
|
|
|
|
|
|
||
|
Менше від –11 °С |
0 |
1 |
1 |
3 |
2 |
0 |
7 |
|
Від –10° до –1 °С |
0 |
0 |
11 |
15 |
13 |
5 |
44 |
|
Від 0° до 10 °С |
10 |
19 |
12 |
13 |
19 |
47 |
120 |
|
Від 11° до 20 °С |
23 |
27 |
15 |
6 |
10 |
2 |
83 |
|
Від 21° до 30 °С |
57 |
32 |
6 |
2 |
1 |
0 |
98 |
|
Більше 31 °С |
9 |
4 |
0 |
0 |
0 |
0 |
13 |
|
Разом днів |
99 |
83 |
45 |
39 |
45 |
54 |
365 |
Підрахуйте частоту спостереження у 2016 році:
1) температури повітря в діапазоні від 11 °С до 20 °С серед тих днів, коли зафіксована вологість не перевищувала 40 %;
2) вологості повітря в діапазоні від 71 % до 80 % серед тих днів, коли зафіксована температура була меншою від 0 °С;
3) температури повітря в діапазоні від 21 °С до 30 °С та одночасно вологості повітря в діапазоні від 41 % до 70 %.
 23. класичне означення ймовірності
23. класичне означення ймовірності
Для знаходження ймовірності деяких подій не обов’язково проводити випробування або спостереження. Достатньо керуватися життєвим досвідом і здоровим глуздом.
![]()
ПРикЛад 1 Нехай у коробці лежать 10 червоних куль. Яка ймовірність того, що взята навмання куля буде червоного кольору? жовтого кольору?
За даних умов будь-яка взята навмання куля буде червоного кольору.
Подію, яка за даним комплексом умов обов’язково відбудеться в будь-якому випробуванні, називають достовірною (вірогідною). Ймовірність такої події вважають рівною 1, тобто:
якщо A — достовірна подія, то
P (A) = 1.
Отже, ймовірність того, що взята навмання куля буде червоного кольору, дорівнює 1.
Оскільки в коробці немає куль жовтого кольору, то взяти кулю жовтого кольору неможливо.
Подію, яка за даним комплексом умов не може відбутися в жодному випробуванні, називають неможливою. Ймовірність такої події вважають рівною 0, тобто:
якщо A — неможлива подія, то
P (A) = 0.
Отже, ймовірність того, що взята навмання куля буде жовтого кольору, дорівнює 0. ◄
![]()
ПРикЛад 2 Однорідну монету підкидають один раз. Яка ймовірність випадіння герба?
У цьому експерименті можна отримати тільки один із двох результатів: випадіння цифри або випадіння герба. Причому жоден із них не має переваг. Такі результати називають рівноможливими, а відповідні випадкові події — рівноймовірними. Тоді природно вважати, що ймовірність кожної з подій «випадіння герба» і «випадіння цифри» дорівнює ![]() .
.
Сказане не означає, що в будь-якій серії експериментів з киданням монети рівно половиною результатів буде випадіння герба
та рівно половиною — випадіння цифри. Ми можемо лише прогнозувати, що за великої кількості випробувань частота випадіння герба приблизно дорівнюватиме ![]() .
.
Розглянемо ще кілька прикладів експериментів з таким комплексом умов, які роблять усі результати експерименту рівноможливими.
![]()
ПРикЛад 3 Гральний кубик (рис. 23.1) кидають один раз. Яка ймовірність випадіння цифри 4?
![]() У цьому експерименті можна отримати один із шести результатів: випаде 1, 2, 3, 4, 5 або 6 очок. Усі ці результати рівноможливі. Тому природно вважати, що ймовірність події «випадіння 4 очок» дорівнює
У цьому експерименті можна отримати один із шести результатів: випаде 1, 2, 3, 4, 5 або 6 очок. Усі ці результати рівноможливі. Тому природно вважати, що ймовірність події «випадіння 4 очок» дорівнює ![]() . ◄
. ◄
![]()
ПРикЛад 4 Нехай випущено 100 000 лотерейних Рис. 23.1
білетів, 20 з яких є виграшними. Яка ймовірність виграшу при купівлі одного білета?
Випробування полягає в тому, що купляють один білет. У цьому експерименті можна отримати один зі 100 000 рівноможливих результатів: купити білет з номером 1, купити білет з номером 2 і т. д. Із них 20 результатів приводять до виграшу. Природно вважати, що ймовірність виграшу при купівлі одного білета дорівнює
![]() =
= ![]() . ◄
. ◄
![]()
ПРикЛад 5 У коробці лежать 15 більярдних куль, пронумерованих числами від 1 до 15. Яка ймовірність того, що вийнята навмання куля матиме номер, кратний 3?
У цьому випробуванні можна отримати один із 15 рівноможливих результатів: вийняти кулю з номером 1, вийняти кулю з номером 2 і т. д. Із них до настання події «вийнята куля має номер, кратний 3» приводять 5 результатів: вийнята куля має номер 3, або 6, або 9, або 12, або 15. Тому природно вважати, що шукана ймовірність дорівнює ![]() . ◄
. ◄
Попри те що в прикладах 1–5 розглядають різні експерименти, їх описує одна математична модель. Пояснимо сказане.
Для тих, хто хоче знати більше
• У кожному прикладі при випробуванні можна отримати один із n рівноможливих результатів.
Приклад 1: n = 10.
Приклад 2: n = 2. Приклад 3: n = 6.
Приклад 4: n = 100 000. Приклад 5: n = 15.
• У кожному прикладі розглядається деяка подія A, до настання якої приводять m результатів. Називатимемо їх сприятливими.
Приклад 1: A — витягнули червону кулю, m = 10, або A — витягнули жовту кулю, m = 0.
Приклад 2: A — випав герб, m = 1.
Приклад 3: A — випала наперед задана кількість очок на грані кубика, m = 1.
Приклад 4: A — виграш призу, m = 20.
Приклад 5: A — витягнули кулю, номер якої кратний 3, m = 5.
• У кожному прикладі ймовірність події A можна обчислити за формулою:
|
m P A( ) = |
Означення. Якщо випробування може закінчитися одним з n рівноможливих результатів, з яких m приводять до настання
m події A, то ймовірністю події A називають відношення ![]() . n
. n
Таке означення ймовірності називають класичним.
Наголосимо, що коли комплекс умов експерименту такий, що його результати не є рівноможливими, то класичне означення ймовірності до такого експерименту застосовувати не можна.
![]()
ПриклаД 6 Кидають одночасно два гральних кубики: синій і жовтий. Яка ймовірність того, що випадуть дві шістки?
За допомогою таблиці, зображеної на рисунку 23.2, ми можемо встановити, що в даному експерименті можна отримати 36 рівноможливих результатів, з яких сприятливим є тільки один. Тому шукана ймовірність дорівнює ![]() . ◄
. ◄

ПРикЛад 7 (задача д’Аламбера).
|
Перша монета |
Друга монета |
|
|
|
|
|
|
|
|
|
|
|
|
Кидають одночасно дві однакові монети. Яка ймовірність того, що хоча б один раз випаде герб?
Ця задача схожа на задачу з прикладу 6. Різниця лише в тому, що кубики відрізнялися за кольором, а монети є нерозрізнимими. Щоби створити в цьому експерименті комплекс умов, за яких усі його результати стануть рівноможливими, будемо розрізняти монети, попередньо їх пронумерувавши. Тоді можна отримати чотири рівноможливих результати (рис. 23.3).
У перших трьох із цих результатів хоча б один раз випав герб. Ці результати є сприятливими. Тому ймовірність того, що при одночасному киданні двох монет хоча б один
раз випаде герб, дорівнює ![]() . ◄ Рис. 23.3
. ◄ Рис. 23.3
Для тих, хто хоче знати більше
![]()
ПриклаД 8 Кидають одночасно два однакових гральних кубики. Яка ймовірність того, що випадуть числа, сума яких дорівнюватиме 11?
Даний експеримент має 11 результатів. Сума чисел, які випали, може дорівнювати 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12. Проте тут помилкою було б вважати, що ймовірність події «сума чисел, які випали, дорівнює 11» становить ![]() . Річ у тім, що перелічені 11 ре - зультатів досліду не є рівноможливими. Наприклад, результат «сума чисел дорівнює 2» може бути отриманий тільки одним способом, а результат «сума чисел дорівнює 6» — п’ятьма способами (переконайтеся в цьому самостійно).
. Річ у тім, що перелічені 11 ре - зультатів досліду не є рівноможливими. Наприклад, результат «сума чисел дорівнює 2» може бути отриманий тільки одним способом, а результат «сума чисел дорівнює 6» — п’ятьма способами (переконайтеся в цьому самостійно).
Щоб мати змогу скористатися класичним означенням ймовірності, опишемо умови експерименту таким чином, щоб усі його результати були рівноможливими.
Для цього будемо умовно розрізняти кубики, наприклад за кольором. Тоді можна отримати 36 рівноможливих результатів
(рис. 23.2). Із них тільки два є сприятливими. Тому шукана ймовірність дорівнює ![]() . ◄
. ◄
![]()
ПриклаД 9 Розглядаються всі сім’ї з двома дітьми, у яких щонайменше одна дитина — хлопчик. Яка ймовірність того, що у вибраній навмання такій сім’ї є два хлопчики? (Вважатимемо, що народження хлопчика та народження дівчинки рівноймовірні.)
Здавалося б, у цій задачі відповіддю є число ![]() . Адже один хлопчик у сім’ї вже є, а отже, другою дитиною з рівною ймовірністю буде або хлопчик, або дівчинка.
. Адже один хлопчик у сім’ї вже є, а отже, другою дитиною з рівною ймовірністю буде або хлопчик, або дівчинка.
Насправді наведені міркування — це розв’язання іншої задачі: розглядаються всі сім’ї з двома дітьми, у яких старша дитина — хлопчик. Яка ймовірність того, що у вибраній навмання такій сім’ї є два хлопчики?
Комплекс умов нашого експерименту дає такі три рівноможливих результати:
старша дитина — хлопчик, молодша дитина — хлопчик; старша дитина — хлопчик, молодша дитина — дівчинка; старша дитина — дівчинка, молодша дитина — хлопчик.
Отже, шукана ймовірність дорівнює ![]() . ◄
. ◄
На завершення цього пункту зазначимо таке.
На перший погляд здається, що багатьма явищами, які відбуваються навколо нас, керує «його величність випадок». Проте при більш ґрунтовному аналізі з’ясовується, що через хаос випадковостей прокладає собі дорогу закономірність, яку можна кількісно оцінити. Науку, яка займається такими оцінками, називають теорією ймовірностей.
1. Яку подію називають достовірною?
2. Яку подію називають неможливою?
3. Яка ймовірність: 1) достовірної події; 2) неможливої події?
4. Наведіть приклади рівноймовірних подій.
5. сформулюйте класичне означення ймовірності.
6. ![]() До яких ситуацій неможливо застосовувати класичне означення ймовірності?
До яких ситуацій неможливо застосовувати класичне означення ймовірності?
ВПРаВи
23.1.° Наведіть приклади достовірних подій.
23.2.° Наведіть приклади неможливих подій.
23.3.° У кошику лежать 10 червоних і 15 зелених яблук. Яка ймовірність взяти навмання з кошика грушу? яблуко?
23.4.° Навмання вибирають три парні цифри. Яка ймовірність того, що число, записане цими цифрами, буде непарним?
23.5.° Навмання вибирають три непарні цифри. Яка ймовірність того, що число, записане цими цифрами, буде непарним?
23.6.° Яка ймовірність того, що, переставивши букви в слові «алгебра», ми отримаємо слово «геометрія»?
23.7.° Наведіть приклади подій з рівноможливими результатами.
23.8.° Наведіть приклади подій з нерівноможливими результатами.
23.9.° Чи рівноймовірні події A і B:
1) подія A: з 15 більярдних куль з номерами від 1 до 15 взяти навмання кулю з номером 1;
подія B: з 15 більярдних куль з номерами від 1 до 15 взяти навмання кулю з номером 7;
2) подія A: з 15 більярдних куль з номерами від 1 до 15 взяти навмання кулю з парним номером;
подія B: з 15 більярдних куль з номерами від 1 до 15 взяти навмання кулю з непарним номером?
дЛЯ тих, хто хоЧе Знати біЛьШе
23.10.° Яка ймовірність того, що при одному киданні грального кубика випаде кількість очок, що дорівнює:
1) одному;
2) ![]() трьом;
трьом;
3) непарному числу;
4) числу, яке кратне 5;
5) числу, яке не ділиться націло на 3; 6) числу, яке кратне 9?
23.11.° Уяви собі, що в класі, у якому ти навчаєшся, розігрується одна безкоштовна туристична поїздка до Лондона. Яка ймовірність того, що до Лондона поїдеш ти?
23.12.° Щоб скласти іспит з математики, потрібно вивчити 35 білетів. Учень вивчив бездоганно 30 білетів. Яка ймовірність того, що, відповідаючи на один навмання витягнутий білет, він отримає оцінку 12 балів?
23.13.° Щоб скласти іспит з математики, треба вивчити 30 білетів. Учень не вивчив тільки один білет. Яка ймовірність того, що він не складе іспит, відповідаючи на один білет?
23.14.° Яка ймовірність того, що ученицю вашого класу, яку викличуть до дошки на уроці математики, зватимуть Катериною?
23.15.° У лотереї 20 виграшних білетів і 280 білетів без виграшу. Яка ймовірність виграти, купивши один білет?
23.16.° У коробці лежать 7 синіх і 5 жовтих кульок. Яка ймовірність того, що вибрана навмання кулька виявиться: 1) жовтою; 2) синьою?
23.17.° У коробці було 23 картки, пронумерованих від 1 до 23. Із коробки навмання взяли одну картку. Яка ймовірність того, що на ній записано число:
1) 11; 2) 24;
3) кратне 6; 4) кратне 5;
5) одноцифрове;
6) складене;
7) у записі якого є цифра 7; 8) у записі якого є цифра 2;
9) у записі якого відсутня цифра 4;
10) сума цифр якого ділиться націло на 3;
11) яке при діленні на 11 дає в остачі 2; 12) у записі якого відсутня цифра 1?
23.18.° З натуральних чисел від 1 до 30 навмання вибирають одне число. Яка ймовірність того, що це число буде:
1) простим;
2) дільником числа 18;
3) квадратом натурального числа?
23.19.° Набираючи номер телефону свого товариша, Микола забув: 1) останню цифру; 2) першу й останню цифри. Яка ймовірність того, що він з першої спроби набере правильний номер?
23.20.• Абонент забув дві останні цифри номера телефону й набирає їх навмання. Яка ймовірність правильно набрати номер, якщо абонент тільки пам’ятає, що дві останні цифри:
1) непарні; 2) різні й парні?
23.21.• Яка ймовірність того, що твій найщасливіший день у наступному році припаде на: 1) 7 число; 2) 31 число; 3) 29 число?
23.22.• Грані кубика пофарбовано в червоний або білий колір (кожну грань в один колір). Ймовірність випадіння червоної грані дорівнює ![]() , а ймовірність випадіння білої грані —
, а ймовірність випадіння білої грані — ![]() . Скільки червоних і скільки білих граней у кубика?
. Скільки червоних і скільки білих граней у кубика?
23.23.• У коробці лежать 4 сині кулі та кілька червоних. Скільки червоних куль у коробці, якщо ймовірність того, що вибрана навмання куля виявиться синьою, дорівнює ![]() ?
?
23.24.• Серед двоцифрових чисел навмання вибирають одне число. Яка ймовірність того, що:
1) його цифра в розряді десятків більша, ніж цифра в розряді одиниць;
2) його цифри в розрядах десятків і одиниць однакові; 3) це число ділиться націло на 9?
23.25.• Картки з номерами 1, 2, 3 довільним чином поклали в ряд. Яка ймовірність того, що картки з непарними номерами опиняться поруч?
23.26.• На лавочку довільним чином сідають два хлопчики й одна дівчинка. Яка ймовірність того, що хлопчики опиняться поруч?
23.27.• У коробці лежать 5 зелених і 7 синіх олівців. Яку найменшу кількість олівців треба вийняти навмання, щоб ймовірність того, що серед вийнятих олівців хоча б один буде зеленого кольору, дорівнювала 1?
Для тих, хто хоче знати більше
23.28.• У коробці лежать 3 червоних, 7 жовтих і 11 синіх олівців. Яку найменшу кількість олівців треба вийняти навмання, щоб ймовірність того, що серед вийнятих олівців хоча б один буде червоного кольору, дорівнювала 1?
23.29.•• Кидають одночасно два гральних кубики. За допомогою рисунка 23.2 установіть, яка ймовірність того, що випадуть:
1) дві одиниці;
2) два однакових числа;
3) числа, сума яких дорівнює 7; 4) числа, сума яких більша за 10;
5) числа, добуток яких дорівнює 6.
23.30.•• Гральний кубик кидають 2 рази. Яка ймовірність того, що:
1) першого разу випаде менше 4 очок, а другого — більше 4; 2) першого разу випаде менше очок, ніж другого; 3) у сумі за два кидки випаде 5 очок?
23.31.•• Яка ймовірність того, що при двох кидках грального кубика:
1) першого разу випаде число, менше від 5, а другого — більше за 4;
2) шістка випаде тільки другого разу;
3) першого разу випаде більше очок, ніж другого?
23.32.•• Дмитро та Петро одночасно кидають по одному гральному кубику. Якщо сума очок, що випали, дорівнює 6, то виграє Дмитро, а якщо в сумі випадає 7 очок, то виграє Петро. У кого з гравців більше шансів виграти у цій грі?
23.33.•• Двічі кидають монету. Яка ймовірність того, що випадуть: 1) два герби; 2) герб і цифра?
23.34.•• Із п’яти пронумерованих карток вибирають навмання одну, запам’ятовують її номер і повертають до решти карток. Потім знову вибирають навмання із цих п’яти карток одну. Яка ймовірність того, що обидва рази витягували картку з одним і тим самим номером?
23.35.•• Яка ймовірність того, що при трьох кидках монети: 1) тричі випаде герб; 2) двічі випаде герб; 3) один раз випаде герб; 4) хоча б один раз випаде герб?
23.36.•• За круглий стіл випадковим чином сіли n людей (n > 2). Із них тільки двоє знайомі один з одним. Яка ймовірність того, що двоє знайомих сядуть поруч?
23.37.•• У чергу випадковим чином стають четверо людей: A, B, C, D. Вважаючи всі варіанти їхнього розміщення рівноможливими, визначте ймовірність того, що A буде стояти попереду B.
спочатку була гра
![]()
Ви знаєте багато ігор, у яких результат залежить від майстерності учасників. Проте є такі ігри, у яких від уміння гравців нічого не залежить. Усе вирішує випадок. До останніх належить гра в кості. Вважають, що саме з неї розпочалася наука про випадкове.
Придворний французького короля Людовіка XIV, азартний гравець, філософ і літератор кавалер де Мере звернувся до видатного вченого Блеза Паскаля з проханням роз’яснити такий парадокс. З одного боку, багатий ігровий досвід де Мере свідчив, що при киданні трьох гральних костей сума в 11 очок випадає частіше, ніж сума у 12 очок.
З другого боку, цей факт вступав у суперечність з такими міркуваннями. Суму в 11 очок можна отримати із шести різних комбінацій кубиків:
|
6–4–1 |
6–3–2 |
5–5–1 |
|
5–4–2 |
5–3–3 |
4–4–3 |
Але й 12 очок теж можна отримати із шести комбінацій:
|
6–5–1 |
6–4–2 |
6–3–3 |
|
5–5–2 |
5–4–3 |
4–4–4 |
Отже, до появи в сумі 11 і 12 очок призводить однакова кількість сприятливих результатів. Таким чином, ці події мають однакові шанси, що суперечить практиці.
Паскаль зрозумів: помилка полягала в тому, що події, які розглядав де Мере, не є рівноймовірними. Наприклад, суму в 11 очок за допомогою комбінації 6–4–1 можна отримати при 6 різних результатах кидання кубиків: (6; 4; 1); (6; 1; 4); (4; 6; 1); (4; 1; 6); (1; 6; 4); (1; 4; 6).
Якщо підрахувати для кожної комбінації кількість способів її виникнення, то отримаємо: для суми 11 кількість сприятливих результатів дорівнює 27, а для суми 12 — 25. Причому всі такі результати є рівноможливими.
Цю та інші задачі, пов’язані з азартними іграми, Блез Паскаль обговорював у листуванні з П’єром Ферма. Вважають, що в цьому листуванні було закладено основи теорії ймовірностей.
Цікаво, що помилку, подібну до тієї, якої припустився де Мере, зробив видатний французький математик Жан Лерон д’Аламбер, розв’язуючи таку задачу: «Монету підкидають двічі. Яка ймовірність того, що хоча б один раз випаде герб?» Він міркував приблизно так.
Можливі три результати: герб випав першого разу, герб випав другого разу, герб узагалі не випав. Тоді з трьох ймовірних результатів сприятливими є тільки два, тобто шукана ймовірність дорівнює ![]() .
.
Проте з прикладу 7 п. 23 ви знаєте, що правильною є відпо- відь ![]() .
.
Помилка полягала в тому, що зазначені три результати не є рівноможливими (подумайте чому). Скоріш за все, ця помилка свідчить про те, що у XVIII ст. теорія ймовірностей була ще «молодою» наукою, яка вимагала уточнення самого поняття «ймовірність події».
Блез Паскаль
(1623–1662)
![]() французький релігійний філософ, письменник, математик і фізик. У ранньому віці виявив математичні здібності, увійшов в історію науки як класичний приклад підліткової геніальності. Коло його математичних інтересів було надзвичайно широким. Зокрема, він винайшов загальний алгоритм для знаходження ознак подільності будь-яких цілих чисел, сформулював ряд основних положень теорії ймовірностей, методи обчислення площ фігур, площ поверхонь і об’ємів тіл. сконструював першу обчислювальну машину-суматор.
французький релігійний філософ, письменник, математик і фізик. У ранньому віці виявив математичні здібності, увійшов в історію науки як класичний приклад підліткової геніальності. Коло його математичних інтересів було надзвичайно широким. Зокрема, він винайшов загальний алгоритм для знаходження ознак подільності будь-яких цілих чисел, сформулював ряд основних положень теорії ймовірностей, методи обчислення площ фігур, площ поверхонь і об’ємів тіл. сконструював першу обчислювальну машину-суматор.
Становлення та розвиток теорії ймовірностей пов’язані з працями таких видатних учених, як Якоб Бернуллі (1654–1705), П’єр-Симон Лаплас (1749–1827), Ріхард фон Мізес (1883–1953). У ХХ ст. особливого значення набули праці видатного радянського математика Андрія Миколайовича Колмогорова.
Українська математична наука подарувала світові плеяду видатних фахівців у галузі теорії ймовірностей. Імена Й. І. Гіхмана, Б. В. Гнєденка, А. В. Скорохода, М. Й. Ядренка відомі математикам у всьому світі.

фундатором Всеукраїнських олімпіад юних математиків. Михайло Йосипович проводив значну просвітницьку діяльність. Зокрема, за його ініціативою в 1968 р. було створено першу в Україні науковопопулярну збірку «У світі математики».
 24. Початкові відомості про статистику
24. Початкові відомості про статистику
Яким тиражем слід видати підручник з алгебри для 9 класу?
Чи варто певному політику висувати свою кандидатуру на чергових виборах мера?
Скільки кілограмів риби та морепродуктів уживає в середньому за рік один житель України?
Чи вигідно для концерту даного артиста орендувати стадіон?
На ці та багато інших запитань допомагає відповідати статистика.
Означення. Статистика (від латин. status — стан) — це наука про отримання, обробку й аналіз кількісних даних, які характеризують масові явища.
Статистичне дослідження складається з кількох етапів:
Зупинимося окремо на кожному етапі.
Збирання даних
Ви знаєте, що шкідливі звички, неправильне харчування, малорухомий спосіб життя призводять до серцево-судинних захворювань. Такого висновку лікарі дійшли, дослідивши, звісно, не всіх людей планети.
Зрозуміло, що дослідження носило вибірковий, але масовий характер.
У статистиці сукупність об’єктів, на основі яких проводять дослідження, називають вибіркою.
У даному прикладі вибірка складалася з кількох мільйонів людей.
Варто зазначити, що статистичний висновок, заснований лише на чисельності вибірки, не завжди є достовірним. Наприклад, якщо ми, досліджуючи популярність артиста, обмежимося опитуванням людей, які прийшли на його концерт, то отримані висновки не будуть об’єктивними, адже вони прийшли на концерт саме тому, що цей артист їм подобається. Статистики говорять, що вибірка має бути репрезентативною (від фр. représentatif — показовий).
Так, лікарі, вивчаючи фактори ризику виникнення серцевосудинних захворювань, досліджували людей різного віку, професій, національностей тощо.
Отже, збирання даних має ґрунтуватися на масовості та репрезентативності вибірки. Інколи вибірка може збігатися з множиною всіх об’єктів, щодо яких проводиться дослідження.
Прикладом такого дослідження є проведення державної підсумкової атестації з математики в 9 класі.
Способи подання даних
Зібрану інформацію (сукупність даних) зручно подавати у вигляді таблиць, графіків, діаграм.
Розглянемо кілька прикладів.
![]() ПРикЛад 1 У таблиці подано результати виступів українських школярів на міжнародних математичних олімпіадах протягом 1993–2016 рр. (Команда учасників на міжнародних математичних олімпіадах складається не більше ніж із 6 осіб.)
ПРикЛад 1 У таблиці подано результати виступів українських школярів на міжнародних математичних олімпіадах протягом 1993–2016 рр. (Команда учасників на міжнародних математичних олімпіадах складається не більше ніж із 6 осіб.)
|
Рік |
Місце проведення |
Кількість медалей |
Без медалей |
|||
|
Золоті |
Срібні |
Бронзові |
Разом медалей |
|||
|
1993 |
Туреччина |
0 |
2 |
3 |
5 |
1 |
|
1994 |
Гонконг |
1 |
1 |
2 |
4 |
2 |
|
1995 |
Канада |
1 |
1 |
1 |
3 |
3 |
|
1996 |
Індія |
1 |
0 |
5 |
6 |
0 |
|
1997 |
Аргентина |
3 |
3 |
0 |
6 |
0 |
|
1998 |
Тайвань |
1 |
3 |
2 |
6 |
0 |
|
1999 |
Румунія |
2 |
2 |
1 |
5 |
1 |
|
2000 |
Республіка Корея |
2 |
2 |
0 |
4 |
2 |
|
2001 |
США |
1 |
5 |
0 |
6 |
0 |
|
2002 |
Велика Британія |
1 |
3 |
0 |
4 |
2 |
|
2003 |
Японія |
1 |
2 |
3 |
6 |
0 |
|
2004 |
Греція |
1 |
5 |
0 |
6 |
0 |
|
2005 |
Мексика |
2 |
2 |
2 |
6 |
0 |
|
2006 |
Словенія |
1 |
2 |
2 |
5 |
1 |
|
2007 |
В’єтнам |
3 |
1 |
2 |
6 |
0 |
|
2008 |
Іспанія |
2 |
2 |
2 |
6 |
0 |
|
2009 |
Німеччина |
3 |
1 |
2 |
6 |
0 |
|
2010 |
Казахстан |
1 |
2 |
3 |
6 |
0 |
|
2011 |
Нідерланди |
1 |
2 |
3 |
6 |
0 |
|
2012 |
Аргентина |
0 |
3 |
2 |
5 |
1 |
|
2013 |
Колумбія |
1 |
3 |
1 |
5 |
1 |
|
2014 |
ПівденноАфриканська Республіка |
2 |
3 |
1 |
6 |
0 |
|
2015 |
Таїланд |
2 |
3 |
1 |
6 |
0 |
|
2016 |
Гонконг |
0 |
2 |
4 |
6 |
0 |
У багатьох випадках дані зручно подавати у вигляді стовпчастої діаграми, яку ще називають гістограмою (від грец. histos — стовп і gramma — написання). Така інформація легко сприймається та добре запам’ятовується.
![]() ПРикЛад 2 На рисунку 24.1 подано інформацію про природнозаповідний фонд України.
ПРикЛад 2 На рисунку 24.1 подано інформацію про природнозаповідний фонд України.
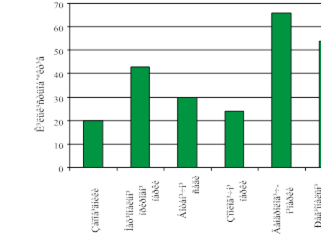
Êàòåãîð³ÿ îá'ºêò³â
Рис. 24.1
![]() ПРикЛад 3 Інформацію також можна подавати у вигляді графіків. Так, на рисунку 24.2 зображено графік щорічного відсоткового зростання кількості користувачів Інтернету у світі протягом 1995–2016 рр.
ПРикЛад 3 Інформацію також можна подавати у вигляді графіків. Так, на рисунку 24.2 зображено графік щорічного відсоткового зростання кількості користувачів Інтернету у світі протягом 1995–2016 рр.
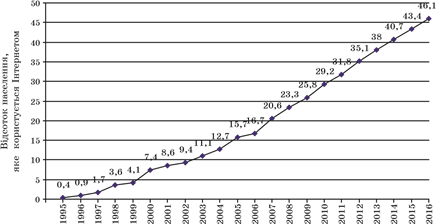
Рис. 24.2
Стовпчасті діаграми та графіки зазвичай використовують тоді, коли хочуть продемонструвати, як з плином часу змінюється деяка величина.
![]() ПРикЛад 4 На рисунку 24.3 наведено розподіл медалей, отриманих українськими школярами на міжнародних олімпіадах у 2016 р. Для цього використано кругову діаграму: круг зображає загальну кількість медалей, а кожному предмету відповідає певний сектор круга.
ПРикЛад 4 На рисунку 24.3 наведено розподіл медалей, отриманих українськими школярами на міжнародних олімпіадах у 2016 р. Для цього використано кругову діаграму: круг зображає загальну кількість медалей, а кожному предмету відповідає певний сектор круга.
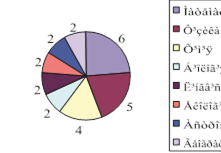
Рис. 24.3
Аналіз даних, висновки та рекомендації
Статистичні відомості надходять з різних галузей знань і діяльності людини: економіки, медицини, соціології, демографії, сільського господарства, метеорології, спорту тощо. Проте статистичні методи обробки (аналізу) даних багато в чому схожі. Ознайомимося з деякими з них.
Звернемося до прикладу 1. Наведена таблиця дозволяє дізнатися, скільки в середньому медалей за рік виборювали школярі України на міжнародних математичних олімпіадах. Для цього потрібно кількість усіх медалей, отриманих протягом періоду, що розглядається, поділити на кількість років. Наприклад, за період 1993–2016 рр. маємо:
![]() =
=
![]() =130=5 5 .
=130=5 5 .
24 12
Оскільки за рік можна вибороти не більше ніж 6 медалей, то знайдене середнє значення 5![]() свідчить про те, що команда України гідно виступає на цьому престижному форумі.
свідчить про те, що команда України гідно виступає на цьому престижному форумі.
У статистичній інформації середні значення отриманих сукупностей даних трапляються досить часто. Наприклад, наведемо таблицю реалізації основних продуктів харчування через мережі великих магазинів у деяких країнах (у кілограмах на людину за рік).
|
Країна |
М’ясо |
Риба та морепродукти |
Зернові |
Овочі |
Фрукти |
|
Австралія |
118,1 |
22,1 |
86,6 |
93,8 |
103,5 |
|
Данія |
111,9 |
24,3 |
139,5 |
102,2 |
146,5 |
|
Іспанія |
122,0 |
27,4 |
98,9 |
143,3 |
105,4 |
|
Італія |
91,0 |
26,2 |
162,6 |
178,3 |
131,0 |
|
Канада |
99,0 |
25,6 |
119,3 |
120,3 |
119,2 |
|
США |
123,4 |
21,1 |
110,8 |
123,5 |
113,5 |
|
Україна |
33,9 |
15,6 |
158,4 |
116,0 |
36,4 |
|
Франція |
98,3 |
31,2 |
117,2 |
142,9 |
95,5 |
Таку таблицю можуть використовувати, наприклад, економісти в дослідженнях, висновках і рекомендаціях, власники магазинів і виробники продукції при плануванні своєї діяльності.
Проте середнє значення не завжди точно (адекватно) відображає ситуацію. Наприклад, якщо в країні доходи різних верств населення дуже різняться, то середній дохід на одну людину для більшості жителів може не відображати їхнього матеріального стану.
Наприклад, у якійсь країні 100 жителів — дуже багаті, а решта 5 мільйонів — дуже бідні. Тоді показник середнього доходу може виявитися не низьким, а отже, неадекватно відображатиме загальну бідність населення.
У подібних випадках для аналізу даних використовують інші характеристики.
За допомогою прикладу 1 складемо таблицю, яка відображає кількість медалей кожного виду:
|
Золоті медалі |
Срібні медалі |
Бронзові медалі |
Без медалей |
|
33 |
55 |
42 |
14 |
Таку таблицю називають частотною, а числа, записані в другому рядку, — частотами.
Частота 55 показує, що українські школярі найчастіше завойовували срібні медалі. Показник «срібні медалі» називають модою отриманих даних.
Це слово всім добре знайоме. Ми часто говоримо: «увійти в моду», «вийти з моди», «данина моді». У повсякденному житті мода означає сукупність поглядів і уподобань, яким більшість віддає перевагу в даний момент часу.
Саме мода є найважливішою характеристикою тоді, коли отримана сукупність даних не є числовою множиною. Продемонструємо це на такому прикладі.
Одна відома фірма, яка планує постачати джинси в Україну, провела опитування репрезентативної вибірки, що складалася з 500 осіб. У результаті отримали таку частотну таблицю:
|
Розмір джинсів |
XS |
S |
M |
L |
XL |
XXL |
XXXL |
|
Частота |
52 |
71 |
145 |
126 |
59 |
40 |
7 |
|
Відносна частота (у %) |
10,4 |
14,2 |
29 |
25,2 |
11,8 |
8 |
1,4 |
У третьому рядку цієї таблиці записано відношення відповідної частоти до величини вибірки. Це відношення, записане у відсотках, називають відносною частотою. Наприклад, для розміру XS маємо:
![]() æ100 = 10 4, (%).
æ100 = 10 4, (%).
Мода даної вибірки — це розмір М, і їй відповідає відносна частота 29 %.
Тим самим фірма отримала інформацію, що найбільшу частину обсягів постачання (приблизно 29 %) мають складати джинси розміру M.
Зауважимо, що якби в таблиці дві частоти були б рівні та набували найбільших значень, то модою були б два відповідних розміри.
Вище ми навели приклад, коли середнє значення не точно відображає матеріальний стан людей у країні. Більш повну характеристику можна отримати, якщо середнє значення доповнити результатом такого дослідження.
Утворюють репрезентативну вибірку, яка складається з людей даної країни, і отримують сукупність даних, яка складається з доходів. Далі відповідно до шкали, яка визначає рівень доходів (низький, середній, високий), розбивають отриманий ряд даних на три групи. Складають таблицю, до якої вносять значення частот і відносних частот:
|
Рівень доходів |
Низький |
Середній |
Високий |
|
Частота |
m |
n |
k |
|
Відносна частота |
p % |
q % |
r % |
Мода такої сукупності даних може характеризувати рівень доходів у країні.
Дослідження сукупності даних можна порівняти з роботою лікаря, який ставить діагноз. Залежно від скарг пацієнта або симптомів, що спостерігаються, лікар вибирає певну методику пошуку причини хвороби. Зрозуміло, що ця методика визначає точність діагнозу. Так само й у статистиці: залежно від зібраної інформації та способу її отримання застосовують різні методи її обробки. Ці методи можуть доповнювати один одного, якийсь із них може точніше (адекватніше), ніж інші, відображати конкретну ситуацію. Так, аналізуючи виступи українських школярів на міжнародних математичних олімпіадах, можна встановити, що статистичні характеристики середнє значення та мода вдало узгоджуються. А в прикладі, який визначає ходовий розмір джинсів, найбільш прийнятним є пошук моди.
Чим більшим є арсенал методик обробки даних, тим об’єктивніший висновок можна отримати.
Ознайомимося ще з однією важливою статистичною характеристикою.
Сім’я вирішила зробити ремонт на кухні та цікавиться, скільки коштує покласти один квадратний метр кахляної плитки. Вивчивши прейскурант 11 будівельних фірм, вони отримали таку інформацію (ціни записано в гривнях у порядку зростання):
80, 80, 90, 90, 100, 130, 180, 200, 300, 450, 500.
Сім’я хоче вибрати фірму із середніми цінами.
Середнє значення отриманої сукупності даних дорівнює 200.
Проте отримані дані показують, що ціну 200 грн скоріше можна віднести до високих, ніж до середніх.
Зазначимо, що число 130 стоїть посередині упорядкованої сукупності даних. Його називають медіаною цієї вибірки. У розглядуваній ситуації саме медіана допомагає вибрати фірму із середніми цінами. Справді, у послідовності з 11 чисел є п’ять менших від 130 і п’ять більших за 130.
Тепер розглянемо упорядковану сукупність даних, яка складається з парної кількості чисел, наприклад з восьми:
1, 4, 4, 7, 8, 15, 24, 24.
Тут «серединою» вибірки є одразу два числа: 7 і 8. Вважають, що медіана такої вибірки дорівнює їхньому середньому арифметичному: ![]() = 7 5, .
= 7 5, .
Середнє значення, моду та медіану називають мірами центральної тенденції отриманої сукупності даних.
![]()
24.1.° Користуючись таблицею середніх річних температур повітря в окремих містах України, побудуйте відповідну стовпчасту діаграму.
|
Місто |
Температура, °C |
Місто |
Температура, °C |
|
Львів |
7,8 |
Черкаси |
7,7 |
|
Ужгород |
10,1 |
Полтава |
7,6 |
|
Київ |
8,4 |
Донецьк |
8,5 |
|
Суми |
6,8 |
Луганськ |
8,8 |
|
Одеса |
10,7 |
Херсон |
10,3 |
|
Миколаїв |
10,0 |
|
|
24.2.° Користуючись таблицею розвитку Київського метрополітену, побудуйте графік зростання довжини його ліній.
24.3.° Користуючись таблицею розвитку Київського метрополітену, побудуйте графік збільшення кількості його станцій.
|
Рік |
Кількість станцій |
Довжина ліній, км |
Рік |
Кількість станцій |
Довжина ліній, км |
|
1960 |
5 |
5,2 |
2000 |
40 |
51,4 |
|
1965 |
10 |
12,7 |
2004 |
43 |
56,3 |
|
1971 |
14 |
18,1 |
2008 |
46 |
59,8 |
|
1976 |
17 |
20,42 |
2010 |
49 |
63,6 |
|
1981 |
23 |
27,72 |
2011 |
50 |
65,08 |
|
1987 |
28 |
32,6 |
2012 |
52 |
66 |
|
1992 |
35 |
43,1 |
2013 |
53 |
67,5 |
24.4.° Визначте, чи є репрезентативною вибірка:
1) щоб дізнатись, як часто жителі міста у вихідні дні бувають на природі, було опитано членів трьох садових кооперативів;
2) з метою виявлення знання дев’ятикласниками напам’ять віршів Лесі Українки випадковим чином було опитано 4 тисячі дев’ятикласників у різних регіонах країни;
3) для визначення відсотка користувачів Інтернету в Україні випадковим чином опитали 500 киян;
4) для з’ясування рейтингу молодіжної телепрограми випадковим чином було опитано 10 тисяч юнаків і дівчат у віці від 15 до 20 років.
24.5.° Знайдіть міри центральної тенденції сукупності даних:
1) 3, 3, 4, 4, 7, 7, 7, 7, 8, 8, 10; 2) 12, 13, 14, 16, 18, 18, 19, 19, 19.
24.6.° Дівчата 9 класу на уроці фізкультури здавали залік зі стрибків у висоту. Учитель записав таку послідовність результатів: 105 см, 65 см, 115 см, 100 см, 105 см, 110 см, 110 см, 115 см, 110 см, 100 см, 115 см.
Знайдіть середнє значення та медіану отриманих даних.
24.7.• Класний керівник 9 класу веде облік відвідування учнями занять. Наприкінці тижня його записи мали такий вигляд:
|
День тижня |
Понеділок |
Вівторок |
Середа |
Четвер |
П’ятниця |
|
Кількість відсутніх |
3 |
2 |
5 |
4 |
8 |
1) Знайдіть, скільки учнів були відсутніми в середньому в день протягом цього тижня.
2) Знайдіть моду отриманих даних.
24.8.• У 9 класі, у якому навчається 23 учні, провели опитування: скільки приблизно годин на день витрачає дев’ятикласник на виконання домашніх завдань. Відповіді учнів подано у вигляді гістограми (рис. 24.4).
×àñ, âèòðà÷åíèé íà âèêîíàííÿ äîìàøí³õ çàâäàíü
Рис. 24.4
1) Заповніть частотну таблицю:
|
Час, витрачений на виконання домашніх завдань, год |
0 |
1 |
2 |
3 |
4 |
|
Частота |
|
|
|
|
|
|
Відносна частота |
|
|
|
|
|
2) Скільки часу на день у середньому витрачає учень цього класу на виконання домашнього завдання? (Знайдіть середнє значення ряду даних.)
3) Скільки часу на виконання домашнього завдання витрачає більшість дев’ятикласників цього класу? (Знайдіть моду ряду даних.)
24.9.• На рисунку 24.5 зображено стовпчасту діаграму результатів письмової роботи з алгебри у трьох дев’ятих класах.
Рис. 24.5 1) Заповніть частотну таблицю:
|
Кількість балів |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
Частота |
|
|
|
|
|
|
|
|
|
|
|
|
|
Відносна частота |
|
|
|
|
|
|
|
|
|
|
|
|
2) Знайдіть середній бал, отриманий учнями за цю письмову роботу.
3) Знайдіть моду отриманих даних.
24.10.• За результатами останньої контрольної роботи з алгебри, яка була проведена у вашому класі, заповніть частотну таблицю, наведену в задачі 24.9.
1) Знайдіть середній бал, отриманий учнями за цю контрольну роботу.
2) Знайдіть моду отриманих даних.
24.11.• Учнів однієї херсонської школи опитали, скільки разів у житті вони літали на літаку. Отримані дані наведено в таблиці:
|
Кількість здійснених польотів |
0 |
1 |
2 |
3 |
4 |
5 |
|
Кількість учнів |
530 |
92 |
46 |
30 |
8 |
4 |
|
Відносна частота (%) |
|
|
|
|
|
|
1) Заповніть третій рядок таблиці.
2) Подайте отримані дані у вигляді стовпчастої діаграми.
3) Знайдіть моду та середнє значення отриманих даних.
4) Поясніть, чи можна вважати вибірку, що розглядається, репрезентативною для висновків щодо всіх школярів м. Херсона.
24.12.• Випишіть усі ваші оцінки з алгебри, отримані протягом року. Знайдіть середнє значення, моду та медіану отриманого ряду даних.
24.13.• Директор фірми отримує 50 000 грн на місяць, два його заступники — по 20 000 грн, а решта 17 робітників фірми — по 4500 грн на місяць. Знайдіть середнє значення, моду, медіану заробітних плат у цій фірмі.
24.14.• Прочитайте один із найвідоміших віршів Т. Г. Шевченка:
Садок вишневий коло хати,
Хрущі над вишнями гудуть,
Плугатарі з плугами йдуть, Співають ідучи дівчата, А матері вечерять ждуть.
Сем’я вечеря коло хати, Вечірня зіронька встає.
Дочка вечерять подає, А мати хоче научати,
Так соловейко не дає.
Поклала мати коло хати Маленьких діточок своїх; Сама заснула коло їх.
Затихло все, тілько дівчата Та соловейко не затих.[11]
Для букв «а», «е», «і», «ї», «н», «о», «р», «у», «ф», «я» складіть частотну таблицю їх наявності в поданому вірші. Визначте моду отриманих даних.
24.15.• Протягом травня 2016 р. температура повітря в Києві о 8 год ранку становила:
|
Дата |
Темпе - ратура, °С |
Дата |
Темпе - ратура, °С |
Дата |
Темпе - ратура, °С |
|
01.05.2016 |
13,1 |
11.05.2016 |
17,8 |
21.05.2016 |
14,0 |
|
02.05.2016 |
15,3 |
12.05.2016 |
15,0 |
22.05.2016 |
16,9 |
|
03.05.2016 |
15,7 |
13.05.2016 |
16,6 |
23.05.2016 |
18,7 |
|
04.05.2016 |
15,4 |
14.05.2016 |
12,6 |
24.05.2016 |
17,4 |
|
05.05.2016 |
16,2 |
15.05.2016 |
13,1 |
25.05.2016 |
16,1 |
|
06.05.2016 |
13,1 |
16.05.2016 |
13,5 |
26.05.2016 |
16,8 |
|
07.05.2016 |
10,5 |
17.05.2016 |
8,8 |
27.05.2016 |
20,1 |
|
08.05.2016 |
14,2 |
18.05.2016 |
12,4 |
28.05.2016 |
19,2 |
|
09.05.2016 |
15,5 |
19.05.2016 |
9,5 |
29.05.2016 |
20,7 |
|
10.05.2016 |
17,5 |
20.05.2016 |
10,8 |
30.05.2016 |
17,3 |
|
|
|
31.05.2016 |
17,4 |
||
Знайдіть міри центральної тенденції отриманих даних.
24.16.• Побудуйте ряд: 1) з п’яти чисел; 2) із шести чисел, у якого:
а) середнє значення дорівнює медіані;
б) середнє значення більше за медіану.
дружимо з комп’ютером
Ви продовжите вдосконалювати навички користування комп’ютером, що їх набули в 7 і 8 класах, опановувати нові інструменти та нові програмні засоби. Нагадаємо, що, крім завдань, наведених у цьому розділі, ви можете використовувати різноманітні програми, створені для вивчення шкільного курсу математики. Ви можете звертатися до глобальної мережі Інтернет для пошуку таких програм та іншої додаткової інформації до курсу алгебри.
Якщо ви плануєте вибрати професію, що потребує постійно використовувати знання з математики, то можна почати опановувати математичні пакети (наприклад, Mathсad, MAtLAB і т. п.), які містять потужний інструментарій для математичних обчислень, геометричних побудов тощо.
У цьому розділі наведено завдання, які ви можете виконувати за допомогою комп’ютера в міру вивчення відповідних тем. Більшість із цих завдань — продовження та розвиток вправ цього підручника (такі вправи позначено піктограмою «¿», а в даному розділі вказано їхні номери).
Для тих, хто любить програмування, пропонуємо створювати алгоритми та програми, у яких використовуватимуться набуті математичні знання. Такі завдання, що містять елементи програмування, позначено зірочкою. Поки ви не вивчили на достатньому рівні яку-небудь мову програмування, досить придумати алгоритм і записати його словами або у вигляді блок-схеми; у міру вивчення мов програмування ви можете реалізовувати ці алгоритми у вигляді програм. Зауважимо, що вміння складати алгоритми (послідовності дій) стане вам у нагоді не тільки в програмуванні, а й в інших областях діяльності.
До п. 1 «Числові нерівності»
Знайдіть у мережі Інтернет правила дорожнього руху. Виберіть із дорожніх знаків ті, що задають гранично допустимі значення яких-небудь числових величин. Запишіть відповідні нерівності.
Нарисуйте за допомогою графічного редактора координатну пряму. Продемонструйте наочно, що менше число розташоване на координатній прямій ліворуч від більшого.
Збережіть рисунок координатної прямої у файлі для використання в наступних завданнях.
Дружимо з комп’ютером
До п. 2 «Основні властивості числових нерівностей»
Яким чином за допомогою графічного редактора продемонструвати властивості числових нерівностей? Які інструменти редактора можна при цьому використати?
До п. 3 «Додавання і множення числових нерівностей. Оцінювання значення виразу»
Знайдіть у мережі Інтернет інформацію про найбільші та найменші відстані від планет Сонячної системи до Сонця. Яким чином можна зробити висновок про найбільші та найменші відстані між кожними двома планетами? Складіть таблицю за допомогою табличного редактора. Чи можете ви зробити так, щоб найбільша та найменша відстані між кожною парою планет обчислювалися автоматично?
До п. 4 «Нерівності з однією змінною»
Нарисуйте за допомогою графічного редактора координатну пряму. Проілюструйте розв’язання прикладів 4.5, 4.6, 4.13. Які інструменти графічного редактора допомогли наочно продемонструвати хід розв’язування?
До п. 5 «Розв’язування лінійних нерівностей з однією змінною.
Числові проміжки»
Виконайте завдання 5.1, 5.2, 5.3 за допомогою графічного редактора.
До п. 6 «Системи лінійних нерівностей з однією змінною»
Виконайте завдання 6.3, 6.4 за допомогою графічного редактора.
* 6.33. Запишіть алгоритм для розв’язування цієї задачі методом перебору.
* 6.54, 6.55, 6.56. Ці три задачі являють собою три типових приклади задач на відсотки. Опишіть кожну з них у загальному випадку, створіть математичну модель, опишіть вхідні й вихідні дані задачі та запишіть алгоритм розв’язування.
До п. 7 «Повторення та розширення відомостей про функцію»
Які способи задання функції є зручними для того, щоб подати цю функцію за допомогою комп’ютера? Які інструменти для цього можна використати?
До п. 8 «Властивості функції»
* Функцію задано таблично. Запишіть алгоритм для пошуку про-міжків знакосталості та алгоритм для пошуку проміжків зростання
Дружимо з комп’ютером
і спадання функції. Яку умову має задовольняти розташування інформації у цій таблиці?
* 8.31. Складіть математичну модель цієї задачі в загальному вигляді. Запишіть алгоритм розв’язування цієї задачі в загальному вигляді.
До п. 9 «Як побудувати графік функції y = kf (x), якщо відомо графік функції y = f (x)»
За допомогою табличного редактора задайте яку-небудь функцію y = f (x) таблично та побудуйте на підставі таблиці графік цієї функції. Які зміни треба внести до таблиці, щоб отримати графік функції y = kf (x)? Як зробити це автоматично? Побудуйте таким чином кілька графіків функції y = kf (x) для різних значень k.
Побудуйте графік якої-небудь функції y = f (x) за допомогою графічного редактора. Які інструменти графічного редактора треба використати, щоб отримати із цього графіка графік функції y = kf (x) при k > 1; при 0 < k < 1; при k = –1? Як можна використати ці інструменти, щоб отримати графік функції y = kf (x) при k < 0 і k ≠ –1?
До п. 10 «Як побудувати графіки функцій y = f (x) + b і y = f (x + a), якщо відомо графік функції y = f (x)»
За допомогою табличного редактора задайте яку-небудь функцію y = f (x) таблично та побудуйте на підставі таблиці графік цієї функції. Які зміни треба внести до таблиці, щоб отримати графік функції y = f (x) + b? y = f (x + a)? y = f (x + a) + b? Як зробити це автоматично? Побудуйте таким чином кілька графіків функції y = f (x + a) + b для різних значень a і b.
Побудуйте графік якої-небудь функції y = f (x) за допомогою графічного редактора. Які інструменти графічного редактора треба використати, щоб отримати із цього графіка графік функції y = f (x) + b? y = f (x + a)? Як можна використати ці інструменти, щоб отримати графік функції y = f (x + a) + b?
До п. 11 «Квадратична функція, її графік і властивості»
* Параболу задано формулою y = ax2 + bx + c. Запишіть алгоритм, вхідними даними для якого є значення a, b, c. Алгоритм має визначити такі характеристики параболи: напрям віток, координати вершини, точки перетину з осями координат, на підставі чого зробити висновок, яку частину параболи доцільно зобразити на графіку.
Автоматизуйте процес складання відповідної таблиці значень функції та побудуйте графік за отриманою таблицею. Як ви будете
Дружимо з комп’ютером
вибирати значення аргументу функції для цієї таблиці, щоб графік став якомога точнішим?
 До оповідання «Про деякі перетворення графіків функцій»
До оповідання «Про деякі перетворення графіків функцій»
Визначте, яким чином за допомогою табличного редактора і графічного редактора з графіка функції y = f (x) отримати графіки функцій y = f (–x), y = f (| x |), y = | f (x) |.
До п. 12 «Розв’язування квадратних нерівностей»
* Користуючись таблицею, наведеною в п. 12, запишіть алгоритм для розв’язування квадратної нерівності ax2 + bx + c > 0, вхідними даними для якого є значення a, b, c.
Які вхідні дані треба додати до цього алгоритму та як змінити його, щоб можна було розв’язувати також нерівності ax2 + bx + c < 0, ax2 + bx c+ l 0, ax2 + bx c+ m 0?
До п. 13 «Системи рівнянь із двома змінними»
Остап Забудько захотів розв’язати систему рівнянь таким чином: для кожного з них побудувати графік рівняння, задавши в табличному редакторі таблицю відповідних значень, а потім знайти на екрані комп’ютера точки перетину цих графіків. У чому полягають недоліки цього плану?
До п. 14 «Система двох рівнянь із двома змінними як математична модель прикладної задачі»
* Проаналізуйте задачі цього пункту. Багато з них описують схожі ситуації. Чи можете ви знайти такі задачі та записати алгоритм їхнього розв’язування в загальному вигляді?
До п. 15 «Числові послідовності»
У табличному редакторі можна заповнити клітинки таблиці членами послідовності, заданої за допомогою формули n-го члена послідовності та за допомогою рекурентної формули. Опануйте ці способи заповнення таблиці.
Зауваження. Очевидно, що в такий спосіб можна сформувати тільки скінченну послідовність.
Використайте ці способи для виконання деяких завдань цього пункту на ваш вибір.
До п. 16 «Арифметична прогресія»
У табличному редакторі створіть механізм для заповнення клітинок таблиці членами скінченної арифметичної прогресії. Зробіть
Дружимо з комп’ютером
так, щоб цей механізм можна було використовувати для отримання арифметичної прогресії з будь-якими значеннями a1 і d.
До п. 17 «Сума n перших членів арифметичної прогресії»
Створіть у табличному редакторі таблицю, перший стовпчик якої містить натуральне число k — номер члена арифметичної прогресії, другий — значення k-го члена, третій — суму k перших членів арифметичної прогресії. Максимальне значення k виберіть на свій розсуд. Чи можете ви повністю автоматизувати побудову цієї таблиці за даними значеннями a1 і d?
До п. 18 «Геометрична прогресія»
У табличному редакторі створіть механізм для заповнення клітинок таблиці членами скінченної геометричної прогресії. Зробіть так, щоб цей механізм можна було використовувати для отримання геометричної прогресії з будь-якими значеннями b1 і q.
Як використовувати калькулятор для обчислень за формулою складних відсотків? Розв’яжіть задачі 18.17–18.20 за допомогою калькулятора.
До п. 19 «Сума n перших членів геометричної прогресії»
У завданні до п. 17 ви створили таблицю, яка будує арифметичну прогресію із заданими a1 і d. Доповніть цю таблицю четвертим стовпцем, який містить величину k-го члена геометричної прогресії, у якої b1 = a1, q = d, і п’ятим стовпцем, який містить суму перших k членів цієї геометричної прогресії. Побудуйте графік на основі цієї таблиці.
Дослідіть поведінку цих арифметичної та геометричної прогресій для різних значень a1 і d.
![]()
Відповіді та вказівки до вправ
§ 1. нерівності
1. Числові нерівності
1.10. 1) Ні; 2) так; 3) ні; 4) ні; 5) ні. 1.18. Значення дробу збільшиться. 1.19. Значення дробу зменшиться або не зміниться. 1.22. 1) Ні; 2) так. 1.26. Так. 1.28. 1) Вказівка. a2 + b2 + 6a – 4b + 13 = = (a2 + 6a + 9) + (b2 – 4b + 4).
2. Основні властивості числових нерівностей
2.13. 3) Порівняти неможливо. 2.19. 4) Якщо c > 0, то c2 > –4c; якщо –4 < c < 0, то c2 < –4c; якщо c = 0, то правильну нерівність отримати не можна. 2.21. 1. 2.22. 24.
3. Додавання і множення числових нерівностей. Оцінювання значення виразу
3.12. 3) Ні; 4) ні; 5) ні; 6) так; 8) так; 10) так; 11) ні; 12) так;
![]() 13) ні; 14) ні. 3.27. 1) 10 + 6 > 11 + 5; 2) 2 + 11 < 5 + 10; 3) 15 − 5 > 2; 4) 21 + 20 > 9. 3.28. 1) 6 + 3 > 7 + 2; 2) 26 − 2 < 14. 3.32. 400 %.
13) ні; 14) ні. 3.27. 1) 10 + 6 > 11 + 5; 2) 2 + 11 < 5 + 10; 3) 15 − 5 > 2; 4) 21 + 20 > 9. 3.28. 1) 6 + 3 > 7 + 2; 2) 26 − 2 < 14. 3.32. 400 %.
4. Нерівності з однією змінною
4.15. 4) Коренів немає; 5) x — будь-яке число; 6) –6. 4.16. 6 км.
5. Розв’язування лінійних нерівностей з однією змінною.
Числові проміжки
![]() −×; 6 ; 7) (−×; −7 5, ];
−×; 6 ; 7) (−×; −7 5, ];
5.25. 3) (−×; −5]; 4) (−×; 1); 5) [7; +×); 6)
11
8) (1; +×); 9) (−× ×; + ); 10) ∅; 11) (−× ×; + ); 12) (−×; 0).
5.26. 1) ![]() 24; +×; 2) [−6; +×); 3) ∅; 4) (−×; −6]; 5) (−× ×; + );
24; +×; 2) [−6; +×); 3) ∅; 4) (−×; −6]; 5) (−× ×; + );
19
6) (−3 5, ; +×). 5.27. 1) –8; 2) –1. 5.28. 1) –6; 2) –3. 5.29. 5 розв’язків.
5.30. 8 розв’язків. 5.33.![]() ; 2) am1,6. 5.34. 1) b < 3; 2) b
; 2) am1,6. 5.34. 1) b < 3; 2) b![]() .
.
5.35. 12 км. 5.36. Таких чисел не існує. 5.37. 18 куль. 5.38. 44 вишні. 5.39. 21. 5.40. 28, 30, 32. 5.41. 25, 30, 35. 5.42. 1) При −4 mx < 2 і x > 2; 2) при x < –4 і −4 < xm3; 3) при –3 < x < –2, –2 < x < 2 і x > 2; 4) при –1 < x < 1 і x > 1. 5.43. 1) При x < –3 і −3 < xm 9;
2) при 7 < x < 8 і x > 8. 5.44. 1) 9; 2) –3; 3) 13; 2,2; 4) коренів немає. 5.45.![]() ; 2) –2; 12. 5.48. 3) При a > –1 і a ≠ 1. 5.49. 2) При m < 7 і m ≠ 0. 5.50. 1) При a > –1 і a ≠ 0; 2) при a
; 2) –2; 12. 5.48. 3) При a > –1 і a ≠ 1. 5.49. 2) При m < 7 і m ≠ 0. 5.50. 1) При a > –1 і a ≠ 0; 2) при a![]() і a ≠ –1;
і a ≠ –1;
3) при a![]() і a ≠ 3. 5.51. При a
і a ≠ 3. 5.51. При a ![]() 1) 3; 2) –1. 5.53. 1) –7;
1) 3; 2) –1. 5.53. 1) –7;
2) –4. 5.54. 1) Якщо a > 0, то x > 0; якщо a < 0, то x < 0; якщо a = 0,
1 1
то розв’язків немає; 2) якщо a > 0, то x < ![]() ; якщо a < 0, то x >
; якщо a < 0, то x > ![]() ; a a
; a a
якщо a = 0, то x — будь-яке число; 3) якщо a > 0, то xl1; якщо a < 0, то xm1; якщо a = 0, то x — будь-яке число; 4) якщо a < 2, то x < –2; якщо a > 2, то x > –2; якщо a = 2, то розв’язків немає; 5) якщо a > 2, то x > a + 2; якщо a < 2, то x < a + 2; якщо a = 2, то розв’язків немає; 6) якщо a > –3, то x am − 3; якщо a < –3, то x al − 3; якщо a = –3, то x — будь-яке число. 5.55. 1) Якщо a ≠ 0, то xm 0; якщо
a = 0, то x — будь-яке число; 2) якщо a > –1, то x < ![]() 2 −a; якщо a+ 1
2 −a; якщо a+ 1
![]() a < –1, то x > 2 −a; якщо a = –1, то x — будь-яке число; 3) якщо a+ 1
a < –1, то x > 2 −a; якщо a = –1, то x — будь-яке число; 3) якщо a+ 1
a > –4, то x > 1 ; якщо a < –4, то x < ![]() 1 ; якщо a = –4, то a+ 4 a+ 4
1 ; якщо a = –4, то a+ 4 a+ 4
розв’язків немає. 5.59. 15 год, 10 год.
6. Системи лінійних нерівностей з однією змінною
![]()
![]() 1 13 −0 8, ; +×); 5) 5;
1 13 −0 8, ; +×); 5) 5;
6.23. 1) ; ; 2) (−×; −4 2, ); 3) [–2; 3]; 4) [
7 10 7
![]() − 1; − 3 ; 2) [−10; +×); 3) ∅;
− 1; − 3 ; 2) [−10; +×); 3) ∅;
6) (−×; −4]; 7) ∅; 8) ∅. 6.24. 1)
2 8
4) (−× ×; + ). 6.25. 1) –3; –2; –1; 0; 2) 7; 8; 9; 10; 11. 6.26. 1) 4 роз-
![]() − 5; 3; 3) ∅; 4) (−×; 4). в’язки; 2) 6 розв’язків. 6.27. 1) [2 5, ; +×); 2) 3
− 5; 3; 3) ∅; 4) (−×; 4). в’язки; 2) 6 розв’язків. 6.27. 1) [2 5, ; +×); 2) 3
6.28. 1) (0; 8]; 2) (5; +×). 6.29. 1) (–0,5; 6,5); 2) [14; 17].
1
6.30. 1) [–1,5; 2,5); 2) 0; ![]() 3 . 6.31. 2) (1,5; 7); 3) (−×; −2). 6.32. 1) ∅;
3 . 6.31. 2) (1,5; 7); 3) (−×; −2). 6.32. 1) ∅;
2) (1; 3). 6.33. 3 см, 5 см або 4 см, 4 см. 6.34. 1) [–4; 3]; 2) x < –1 або x > 3,5; 3) x < 1 або x > 8; 4) (–2; 9); 5) (–2; 0,5]; 6) xm−0,8 або x > 6. 6.35. 1) (–3; 2); 2) x < 4 або x > 8; 3) x < –9 або xl1,2; 4) − ![]() 14; 10. 6.36. 1) [–1,6; 5,6]; 2) (–4; 1); 3) x < –12 або x > 6;
14; 10. 6.36. 1) [–1,6; 5,6]; 2) (–4; 1); 3) x < –12 або x > 6;
![]()
![]() 8 −11; +×. 6.37. 1) xm3,6 або
8 −11; +×. 6.37. 1) xm3,6 або
4) xm2 або xl ; 5) [1; +×); 6)
3 7
xl 8,4; 2) [–2; –1,2]; 3) −×; ![]() 1 ; 4) (–∞; 2]. 6.38. 1) При a > 3; 2) при
1 ; 4) (–∞; 2]. 6.38. 1) При a > 3; 2) при
2
![]()
![]()
![]() am3. 6.39. 1) При am 4; 2) при a > 1. 6.40. 1) При am−1; 2) при a = 1. 6.41. Якщо a < 2, то x am ; якщо al 2, то x < 2. 6.42. Якщо a < –3, то a < x < –3; якщо al −3, то розв’язків немає. 6.43. При 10 < am11. 6.44. При 1 < bm2. 6.45. При 8 ma < 9. 6.46. При −6 mb < −5. 6.47. При a < 3. 6.48. При −
am3. 6.39. 1) При am 4; 2) при a > 1. 6.40. 1) При am−1; 2) при a = 1. 6.41. Якщо a < 2, то x am ; якщо al 2, то x < 2. 6.42. Якщо a < –3, то a < x < –3; якщо al −3, то розв’язків немає. 6.43. При 10 < am11. 6.44. При 1 < bm2. 6.45. При 8 ma < 9. 6.46. При −6 mb < −5. 6.47. При a < 3. 6.48. При −![]() m ma 3. 6.49. При a < –7 або a > 8. 6.50. 1) –1; 2) –2; 4. 6.51. 1) 2 10 − 6; 2) 0,5 2b; 3) −4 6.
m ma 3. 6.49. При a < –7 або a > 8. 6.50. 1) –1; 2) –2; 4. 6.51. 1) 2 10 − 6; 2) 0,5 2b; 3) −4 6.
§ 2. квадратична функція
7. Повторення та розширення відомостей про функцію
7.17. 2) Усі числа, крім 7 і –7; 4) усі числа, не менші від 4, крім числа 6. 7.27. 60 км/год.
8. Властивості функції
8.17. a < ![]() . 8.18. a > 9. 8.19. 2. 8.20. m < –2. 8.26. a = 1, a = 2 і a = 1,5. 8.27. Якщо a < –2, то найбільше значення fнайб = f (a) = a2, найменше значення fнайм = f (0) = 0; якщо a = –2, то fнайб = f (–2) = = f (2) = 4, fнайм = f (0) = 0; якщо −2 < am 0, то fнайб = f (2) = 4, fнайм = f (0) = 0; якщо 0 < a < 2, то fнайб = f (2) = 4, fнайм = f (a) = a2.
. 8.18. a > 9. 8.19. 2. 8.20. m < –2. 8.26. a = 1, a = 2 і a = 1,5. 8.27. Якщо a < –2, то найбільше значення fнайб = f (a) = a2, найменше значення fнайм = f (0) = 0; якщо a = –2, то fнайб = f (–2) = = f (2) = 4, fнайм = f (0) = 0; якщо −2 < am 0, то fнайб = f (2) = 4, fнайм = f (0) = 0; якщо 0 < a < 2, то fнайб = f (2) = 4, fнайм = f (a) = a2.
8.30. 10 год, 40 год. 8.31. 20 %.
9. Як побудувати графік функції y = k f (x), якщо відомо графік функції y = f (x)
9.21. 3 т.
10. Як побудувати графіки функцій y = f (x) + b і y = f (x + a), якщо відомо графік функції y = f (x)
10.17. а) y = x2 + 3; б) y = –2x2 – 1. 10.18. а) y = 2x2 – 6; б) y =
= 4 – x2. 10.19. a) y = (x – 2)2; б) y = –3 (x + 3)2. 10.20.a) y = ![]() (x + 4)2;
(x + 4)2;
б) y = –2 (x – 1)2. 10.21. a) y = (x + 2)2 – 4; б) y = –(x – 2)2 + 5;
в) y = ![]() (x − 3)2 + 1. 10.22. a) y = (x – 4)2 – 5; б) y = –2 (x + 6)2 + 7.
(x − 3)2 + 1. 10.22. a) y = (x – 4)2 – 5; б) y = –2 (x + 6)2 + 7.
10.25. Обидва твердження є правильними. 10.28. 3) Вказівка.
y = ![]() −2x+ −2 2 = −2 −
−2x+ −2 2 = −2 − ![]() 2 . 10.32.
2 . 10.32. ![]() 3. x− 1 x− 1 4
3. x− 1 x− 1 4
11. Квадратична функція, її графік і властивості
11.12. –1; 1; 3. 11.13. 4. 11.14. 1) 2 корені; 2) 1 корінь.
11.15. 3 корені. 11.16. 1) (–1; –1), (9; 9); 2) (2; 23), (8; 17). 11.17. (3; 15),
(–1; 11). 11.23. 1) –25; 2) –13; 3) –22. 11.24. 1) 26; 2) 17; 3) –10. 11.25. p = 1, q = 4. 11.26. a = −![]() , b =
, b = ![]() . 11.27. a = 3, b = 5.
. 11.27. a = 3, b = 5.
11.30. b = –16. 11.31. b = 18. 11.32. a = 1 або a = 4. 11.33. al![]() .
.
11.34. a < –16. 11.35. c = –8. 11.36. c = 14. 11.37. а) a > 0, b < 0, c < 0; б) a < 0, b < 0, c > 0. 11.39. p = –4, q = 9. 11.40. a = 1, b = –8, c = 6. 11.41. а) –4; б) 4. 11.42. –1. 11.43. 1) 25. Вказівка. Нехай одне із чисел дорівнює x, тоді друге число дорівнює 10 – x. Розгляньте функцію f (x) = x (10 – x) = 10x – x2; 2) 50. 11.44. Через 1 год
![]()
![]() 30 хв. 11.45. 1600 м2. 11.50. 1) a > –4; 2) a = –4; 3) a < –4. 11.52. a >
30 хв. 11.45. 1600 м2. 11.50. 1) a > –4; 2) a = –4; 3) a < –4. 11.52. a > ![]() . 11.53. al −0,5. 11.57. 1) 8a a; 2) 56; 3) 6 2 − 5.
. 11.53. al −0,5. 11.57. 1) 8a a; 2) 56; 3) 6 2 − 5.
11.58. 4 км/год. 11.59. 20 хв, 30 хв.
12. Розв’язування квадратних нерівностей
12.10. 1) (–2; 1); 2) (−×; −5] Ÿ [2; +×); 3) −3; − ![]() 13 ; 4) (−×; − 21) Ÿ
13 ; 4) (−×; − 21) Ÿ
Ÿ (1; +×); 5) (−×; −3) Ÿ (4; +×); 6) −13![]() 3 ; 1 . 12.11. 1) (−×; 1] Ÿ [4; +×);
3 ; 1 . 12.11. 1) (−×; 1] Ÿ [4; +×);
![]()
![]() 1 1 −×; −10) Ÿ (1; +×). 12.12. 1) При − 1 < x < 7 ;
1 1 −×; −10) Ÿ (1; +×). 12.12. 1) При − 1 < x < 7 ;
2) (–5; –3); 3) ; ; 4) (
6 2 3 3
2) при xm−0,2 або xl 2,4. 12.13. 1) При −![]() < x <
< x < ![]() ; 2) при
; 2) при
−![]() m mx
m mx ![]() . 12.14. При –5 < x < 4. 12.15. При 1 < x < 2,5. 12.16. 1) –5, –4,
. 12.14. При –5 < x < 4. 12.15. При 1 < x < 2,5. 12.16. 1) –5, –4,
–3, –2, –1, 0; 2) –3, –2, –1, 0, 1, 2, 3; 3) 0; 4) –1, 0, 1, 2, 3, 4, 5. 12.17. 1) 11; 2) 4. 12.18. 1) –6; 2) –2. 12.19. 1) 1; 2) –3.
12.24. 1) –4 < a < 4; 2) –8 <a < 12; 3) ![]() < a <
< a < ![]() . 12.25. 1) b < −
. 12.25. 1) b < −![]() або b > 1; 2) b < 4 або b > 10. 12.26. 1) (0; 3]; 2) [−4; −0 5, ] Ÿ [6; +×);
або b > 1; 2) b < 4 або b > 10. 12.26. 1) (0; 3]; 2) [−4; −0 5, ] Ÿ [6; +×);
![]() −×; 12 Ÿ 53; 3; 2) (−2; 0] Ÿ 3) [−1; 0) Ÿ (6; 10]; 4) (–5; –3]. 12.27. 1)
−×; 12 Ÿ 53; 3; 2) (−2; 0] Ÿ 3) [−1; 0) Ÿ (6; 10]; 4) (–5; –3]. 12.27. 1)
Ÿ [5; 9 .) 12.28. 1) –4, –3, –2, –1, 0, 1; 2) –3, –2, 1, 2. 12.29. 1) (6; +×);
2) (−3; 5) Ÿ (5; 6); 3) (−×; −9) Ÿ (−9; −2] Ÿ [7; 9) Ÿ (9; +×); 4) −1; ![]() 2 .
2 .
3
12.30. 1) [–2; 2); 2) (−5; 6) Ÿ (6; 7). 12.31. 1) (–11; 11); 2) −×; − ![]() 18 Ÿ
18 Ÿ
Ÿ ![]() 18; +×. 12.32. 1) (−×; −1] Ÿ [−0 4, ; 0 4, ] Ÿ [1; +×); 2) [–2; 2].
18; +×. 12.32. 1) (−×; −1] Ÿ [−0 4, ; 0 4, ] Ÿ [1; +×); 2) [–2; 2].
12.33. 1) (−5; 0) Ÿ (0; 2); 2) [0; 2]; 3) (−1; 2) Ÿ (2; 9); 4) (−×; −5) Ÿ Ÿ (−5; −3) Ÿ (5; +×); 5) (−×; −8] Ÿ [1; 4) Ÿ (4; +×); 6) [−11; −3) Ÿ (−3; 1].
12.34. 1) (−×; 0) Ÿ (0; 2) Ÿ (3; +×); 2) (4; +×); 3) (−×; −3) Ÿ (−3; −2) Ÿ
Ÿ (3; +×); 4) − ![]() 13; 1Ÿ (1; 3]. 12.35. 1) (−4; −3) Ÿ (5; +×); 2) [−4; −3] Ÿ
13; 1Ÿ (1; 3]. 12.35. 1) (−4; −3) Ÿ (5; +×); 2) [−4; −3] Ÿ
Ÿ [5; +×); 3) (−×; −4); 4) (−×; −4] Ÿ {−3, 5}. 12.36. 1) (3; 7);
2) [3; 7] Ÿ {−2}; 3) (–2; 3); 4) [−2; 3] Ÿ {7}. 12.37. 1) При a > 4; 2) при
−1 m ma ![]() ; 3) при 0 < a <
; 3) при 0 < a < ![]() ; 4) при a >
; 4) при a > ![]() . 12.38. 1) При al 9;
. 12.38. 1) При al 9;
2) при 3 m ma 7; 3) при al1. 12.39. 1) Якщо a < 1, то a < x < 1 або x > 4; якщо 1 m ma 4, то x > 4; якщо a > 4, то x > a; 2) якщо am−![]() , то розв’язків немає; якщо −
, то розв’язків немає; якщо −![]() < am1, то −
< am1, то −![]() mx a< ; якщо a > 1, то
mx a< ; якщо a > 1, то
−![]() m mx 1. 12.40. 1) Якщо am−8, то –8 < x < 9; якщо –8 < a < 9, то a < x < 9; якщо al 9, то розв’язків немає; 2) якщо a < 1, то x < a; якщо 1 m ma 8, то x < 1; якщо a > 8, то x < 1 або 8 < x < a.
m mx 1. 12.40. 1) Якщо am−8, то –8 < x < 9; якщо –8 < a < 9, то a < x < 9; якщо al 9, то розв’язків немає; 2) якщо a < 1, то x < a; якщо 1 m ma 8, то x < 1; якщо a > 8, то x < 1 або 8 < x < a.
12.43. 3 дні. 12.44. 40 л.
13. Системи рівнянь із двома змінними
13.3. 1) (5; 8), (–3; 0); 2) (4; 1), (1; 4); 3) (–1; 1), (–3; –1); 4) (6; 1), (–6; –2); 5) (5; 3), (–1,5; –10); 6) (2; –2). 13.4. 1) (–4; –7), (7; 4); 2) (2; 4), (–5; –3); 3) (–1; 4), (–0,5; 2,5); 4) (4; 2), (20; –14). 13.5. 1) 2 розв’язки; 2) 3 розв’язки; 3) 1 розв’язок; 4) 2 розв’язки; 5) розв’язків немає; 6)3 розв’язки. 13.6.1)2 розв’язки; 2) розв’язків немає; 3) 2 розв’язки; 4) 4 розв’язки. 13.7. 1) (4; 3); 2) (0; 0), (–2,4; 4,8); 3) (4; –3), (17; 10); 4) (9; –4), (4; 1); 5) (2; 2,5), (–4,4; –2,3); 6) (4; –1), (0; 3). 13.8. 1) (6; 9), (–9; –6); 2) (1; 0),
17 38 1
![]() (–0,5; 0,75); 3) (2; 4), (3; 3); 4) (1; 1), ; . 13.9. 1)
(–0,5; 0,75); 3) (2; 4), (3; 3); 4) (1; 1), ; . 13.9. 1) ![]() ; 0,
; 0,
3 3 3
2 43
![]() (–2; –7); 2) (2; 2), (–1; –4); 3) (1; 0), (5; –4); 4) (2; 3), ; .
(–2; –7); 2) (2; 2), (–1; –4); 3) (1; 0), (5; –4); 4) (2; 3), ; .
3 9
13.10. (–4; –1). 13.11. 2) (0,5; 5,5); 3) (–4; 52), (3; 3). 13.12. 1) (3; 4),
![]() (4; 6); 2) (–2; 1), −6;
(4; 6); 2) (–2; 1), −6; ![]() 9 . 13.13. 1) (2; 1), 1; − 2 ; 2) (1; 5), 10
9 . 13.13. 1) (2; 1), 1; − 2 ; 2) (1; 5), 10![]() ; −2.
; −2.
5 3 3 3
6 15
![]() 13.14. 1) (–5; 1), (1; –5), (4; 1), (1; 4); 2) (5; –2), ; ; 3) (3; 1),
13.14. 1) (–5; 1), (1; –5), (4; 1), (1; 4); 2) (5; –2), ; ; 3) (3; 1),
7 7
(–3; –1), (2 2; 2 ), (−2 2; − 2 ); 4) (2; 3); 5) (–3; 3), (3; –3);
![]()
![]()
![]() 6) (2; 1), − 1; −4; 7) (1; 0), − 19; − 8 . 13.15. 1) (6; 3), − 3; − 3 ;
6) (2; 1), − 1; −4; 7) (1; 0), − 19; − 8 . 13.15. 1) (6; 3), − 3; − 3 ;
2 21 21 4 2
![]()
![]() 2) (2; –1), 21; 15 ; 3) − 1; 1 ; 4) (9; 3), (–9; –3); 5) (–2; 1),
2) (2; –1), 21; 15 ; 3) − 1; 1 ; 4) (9; 3), (–9; –3); 5) (–2; 1),
53 53 4 2
![]() 29; − 3 ; 6) (–3; 4), (–5; 2), (1; –4), (3; –2). 13.16. 1) (1; 0), (0; 1);
29; − 3 ; 6) (–3; 4), (–5; 2), (1; –4), (3; –2). 13.16. 1) (1; 0), (0; 1);
28 14
2) (3; –1), (1; –3); 3) (4; 3), (–4; –3); 4) (–3; 2), (3; –2). 13.17. 1) (4; 2),
![]() (–2; –4); 2) (1; 3), (–1; –3). 13.18. 1) (1; 2), 7 1; − 1 ; 2) (–7; –5), (4; 6);
(–2; –4); 2) (1; 3), (–1; –3). 13.18. 1) (1; 2), 7 1; − 1 ; 2) (–7; –5), (4; 6);
2 6
![]() 2 − 4 . 13.19. 1) (4; 1), 3) (–4; –3), (–4; 2), (3; –3), (3; 2); 4) (3; 1), ;
2 − 4 . 13.19. 1) (4; 1), 3) (–4; –3), (–4; 2), (3; –3), (3; 2); 4) (3; 1), ;
3 3
![]() 2 − 8 ; 3) (6; 5), (–4; –5); 4) (5; 4), (–5; –4), (5; –4), (1; 4); 2) (1; –2), ;
2 − 8 ; 3) (6; 5), (–4; –5); 4) (5; 4), (–5; –4), (5; –4), (1; 4); 2) (1; –2), ;
3 3
![]()
![]() (–5; 4). 13.20. 1) 7; 1 , 1; 7 ; 2) (–2; 4), (2; –4), 94; − 8 , − 94; 8 ;
(–5; 4). 13.20. 1) 7; 1 , 1; 7 ; 2) (–2; 4), (2; –4), 94; − 8 , − 94; 8 ;
6 6 7 7 7 7
3) (4; 3), (3; 4), (–4; –3), (–3; –4); 4) (1; –1), − ![]() 1; 3, (–1; 1),
1; 3, (–1; 1), ![]() 1; −3.
1; −3.
3 3
13.21. 1) (2; 1), (–5; –0,4); 2) (4; 0); 3) (1; 3), (3; 1), (–3; –1), (–1; –3);
4) ![]()
![]() (–2; 2), −10; 2 , (2; –2), 10; − 2 . 13.22. 1) a = 3 2 або a = −3 2;
(–2; 2), −10; 2 , (2; –2), 10; − 2 . 13.22. 1) a = 3 2 або a = −3 2;
![]()
![]() 5 5
5 5
![]() 2) −3 2 < a < 3 2; 3) a < −3 2 або a > 3 2. 13.23. 1) k = 2 або k = –2; 2) k < –2 або k > 2; 3) –2 < k < 2. 13.24. 1) Якщо a > 0, то 2 розв’язки; якщо a = 0, то 1 розв’язок; якщо a < 0, то розв’язків немає; 2) якщо –4 < a < 4, то розв’язків немає; якщо a = –4 або a = 4, то 2 розв’язки; якщо a < –4 або a > 4, то 4 розв’язки; 3) якщо a > −
2) −3 2 < a < 3 2; 3) a < −3 2 або a > 3 2. 13.23. 1) k = 2 або k = –2; 2) k < –2 або k > 2; 3) –2 < k < 2. 13.24. 1) Якщо a > 0, то 2 розв’язки; якщо a = 0, то 1 розв’язок; якщо a < 0, то розв’язків немає; 2) якщо –4 < a < 4, то розв’язків немає; якщо a = –4 або a = 4, то 2 розв’язки; якщо a < –4 або a > 4, то 4 розв’язки; 3) якщо a > −![]() , то 2 розв’язки; якщо a = −
, то 2 розв’язки; якщо a = −![]() , то 1 розв’язок; якщо a < −
, то 1 розв’язок; якщо a < −![]() , то розв’язків немає; 4) якщо a < −
, то розв’язків немає; 4) якщо a < −![]() або a > 2, то розв’язків немає; якщо a = −
або a > 2, то розв’язків немає; якщо a = −![]() або –2 < a < 2, то 2 розв’язки; якщо
або –2 < a < 2, то 2 розв’язки; якщо
![]()
![]() −
−![]() < a < −2, то 4 розв’язки; якщо a = –2, то 3 розв’язки; якщо a = 2, то 1 розв’язок. 13.25. 1) Якщо a < 1, то розв’язків немає; якщо a = 1, то 2 розв’язки; якщо a > 1, то 4 розв’язки; 2) якщо a > 3 2 або a < –3, то розв’язків немає; якщо a = 3 2 або –3 <
< a < −2, то 4 розв’язки; якщо a = –2, то 3 розв’язки; якщо a = 2, то 1 розв’язок. 13.25. 1) Якщо a < 1, то розв’язків немає; якщо a = 1, то 2 розв’язки; якщо a > 1, то 4 розв’язки; 2) якщо a > 3 2 або a < –3, то розв’язків немає; якщо a = 3 2 або –3 <
![]()
![]()
![]()
![]()
![]()
![]() < a < 3, то 2 розв’язки; якщо 3 < a < 3 2, то 4 розв’язки; якщо a = 3, то 3 розв’язки; якщо a = –3, то 1 розв’язок; 3) якщо −2 2 < a < 2 2, то розв’язків немає; якщо a = −2 2 або a = 2 2, то 2 розв’язки; якщо a < −2 2 або a > 2 2, то 4 розв’язки.
< a < 3, то 2 розв’язки; якщо 3 < a < 3 2, то 4 розв’язки; якщо a = 3, то 3 розв’язки; якщо a = –3, то 1 розв’язок; 3) якщо −2 2 < a < 2 2, то розв’язків немає; якщо a = −2 2 або a = 2 2, то 2 розв’язки; якщо a < −2 2 або a > 2 2, то 4 розв’язки.
13.26. a = –2. Вказівка. Очевидно, що a ≠ 0. Розгляньте систему, що складається з двох рівнянь ax2 + x + 1 = 0 і ax2 + a2x + a = 0.
6 2 14
13.28. 5. 13.29. 0; 17![]() . 13.30. 40. 13.33. 717
. 13.30. 40. 13.33. 717![]() динарія, 917
динарія, 917![]() динарія.
динарія.
13.34. 72 км/год, 10 км/год.
14. Система двох рівнянь із двома змінними як математична модель прикладної задачі
14.1. 9 і 12. 14.2. 6 і 4. 14.3. 80 м, 30 м. 14.4. 7 см, 9 см. 14.5. 36. 14.6. 62. 14.7. 84. 14.8. 12 і 24. 14.9. 6 і 9. 14.10. 5 см, 12 см. 14.11. 15 см, 17 см. 14.12. 15 см і 12 см або 18 см і 10 см. 14.13. 15 см, 6 см. 14.14. 18 см, 12 см. 14.15. 80 км/год, 60 км/год.
14.16. 90 км/год, 45 км/год. 14.17. 80 км/год, 60 км/год. 14.18. 500 м/хв, 400 м/хв. 14.19. 12 днів, 24 дні або 40 днів, 10 днів. 14.20. 10 год, 15 год або 12 год, 12 год. 14.21. 16 год, 48 год. 14.22. 10 год, 15 год. 14.23. 60 Ом, 90 Ом. 14.24. 4 Ом, 6 Ом або 3,6 Ом, 7,2 Ом. 14.25. 2 км/год. 14.26. 27 км/год, 3 км/год. 14.27. 24 км/год, 16 км/год. 14.28. 12 км/год. 14.29. 2 км/год,
12 км/год. 14.30. 8,4 г/см3, 6,4 г/см3. 14.31. 15 Н, 20 Н. 14.32. 60 м,
1 1
![]() 80 м. 14.33. 1) − ; 2) . 14.35. 1) (−×; 2]; 2) (0,16; +×). 14.36. 3.
80 м. 14.33. 1) − ; 2) . 14.35. 1) (−×; 2]; 2) (0,16; +×). 14.36. 3.
a 2 − b
![]() 5 +×. 14.39. 13 і 6
5 +×. 14.39. 13 і 6
14.37. −0 5, m mx 2,4. 14.38. 1) (−×; −2 5, ]; 2) 6; або 67 і 66.
§ 3. Числові послідовності
15. Числові послідовності
15.11. 8 членів. 15.12. 13. 15.13. 1, 2, 3, 4, 5. 15.14. 8.
15.15. 1) an = n2; 2) an = 3n + 2; 3) an = ![]() n− 1; 4) an = (–1)n + 1. n
n− 1; 4) an = (–1)n + 1. n
15.16. 1) an = n3 + 1; 2) an = ![]() 1 . 15.18. 2) [–6; 1). 15.20. 32 деn n( + 1)
1 . 15.18. 2) [–6; 1). 15.20. 32 деn n( + 1)
талі. 15.21. 60 кг. 15.22. 400 сторінок.
16. Арифметична прогресія
16.13. 1) Так, n = 16; 2) ні. 16.14. 15. 16.17. 23. 16.18. –6.
16.20. 18. 16.21. 16. 16.22. –0,6. 16.23. –6; –4,5; –3; –1,5; 0; 1,5; 3. 16.24. 2,2; 0,4; –1,4; –3,2. 16.25. 1) a1 = 5, d = 2,5; 2) a1 = –6, d = 4 або a1 = 15, d = ![]() . 16.26. 1) a1 = –2, d = 3; 2) a1 = 20, d = –8
. 16.26. 1) a1 = –2, d = 3; 2) a1 = 20, d = –8
або a1 = 51,5, d = –11,5. 16.27. Якщо перший член прогресії дорівнює її різниці або різниця прогресії дорівнює нулю. 16.30. 60°.
![]() 16.31. 1) Так, a1 = –3, d = –6; 2) ні; 3) так, a1 = –2,8, d = –2,8; 1
16.31. 1) Так, a1 = –3, d = –6; 2) ні; 3) так, a1 = –2,8, d = –2,8; 1
4) ні. 16.32. 1) Так, a1 = 13, d = 7; 2) так, a1 = ![]() , d = ; 3) ні. 5
, d = ; 3) ні. 5
![]()
![]() 16.38. При x = –1 маємо: a1 = –3, a2 = –2, a3 = –1; при x = 8 маємо: a1 = 60, a2 = 43, a3 = 26. 16.39. y = 3; a1 = 10, a2 = 12, a3 = 14. 16.40. y = 1; a1 = –1, a2 = 8, a3 = 17, a4 = 26. 16.41. x = –1; a1 = a2 = a3 = a4 = 1. 16.45. 1) (7; –1), (11; –5); 2) (2; 2), (2; –2), (–2; 2), (–2; –2). 16.47. –4. 16.48. 1) 120 2; 2) 150 − 30 2.
16.38. При x = –1 маємо: a1 = –3, a2 = –2, a3 = –1; при x = 8 маємо: a1 = 60, a2 = 43, a3 = 26. 16.39. y = 3; a1 = 10, a2 = 12, a3 = 14. 16.40. y = 1; a1 = –1, a2 = 8, a3 = 17, a4 = 26. 16.41. x = –1; a1 = a2 = a3 = a4 = 1. 16.45. 1) (7; –1), (11; –5); 2) (2; 2), (2; –2), (–2; 2), (–2; –2). 16.47. –4. 16.48. 1) 120 2; 2) 150 − 30 2.
16.50. 24 деталі. 16.51. 40 пістолів або 60 пістолів. 16.52. 120 %.
17. Сума n перших членів арифметичної прогресії
17.9. 1) 204; 2) 570. 17.10. –310. 17.11. 156 ударів. 17.12. 1400.
17.13. 710. 17.14. 1188. 17.15.8, 14, 20. 17.16. –17. 17.17. 1 , 10
, 10 ,
,
![]() 1 1 n n( + 1) 2
1 1 n n( + 1) 2
20, 29 , 38 . 17.18. 1) ![]() ; 2) n . 17.19. n (n + 1). 17.20. 3.
; 2) n . 17.19. n (n + 1). 17.20. 3.
6 3 2
17.21. –67,2. 17.22. 63. 17.23. 5880. 17.24. 2112. 17.25. 1632. 17.26. 61 376. 17.27. 70 336. 17.28. 0,3. 17.29. 10. 17.30. 20. 17.31. 16. 17.32. Так, 19, 23, 27, 31, 35. 17.33. Ні. 17.34. 10 с. 17.35. 42 сторінки. 17.36. –1976. 17.37. 348. 17.38. a1 = 14, d = –3. 17.39. –10. 17.40. 10. 17.41. 690. 17.42. 250. 17.43. 1) 12; 2) 26. 17.44. 1) 10; 2) 69. 17.45. a1 = 1, d = 2. 17.47. a1 = –2, d = 2. Вка-
![]() зівка. an = Sn – Sn – 1. 17.48. 2610. 17.52. 1) a − bc; 2) 4 d − 28.
зівка. an = Sn – Sn – 1. 17.48. 2610. 17.52. 1) a − bc; 2) 4 d − 28.
abc 3 d + 18
17.53. 24 км/год. 17.54. 2 год. 17.55. 200 г, 600 г.
18. Геометрична прогресія
18.17. 6298,56 грн. 18.18. 29 736 одиниць. 18.19. 3600 грн. 18.20. 600 грн. 18.21. 5 %. 18.22. На 15 %. 18.25. 1) 2; 2) ![]() або
або
−![]() . 18.26. 1)
. 18.26. 1) ![]() ; 2) 0,001. 18.27. 6. 18.28. 9. 18.29. 30 і 150. 18.30. 1;
; 2) 0,001. 18.27. 6. 18.28. 9. 18.29. 30 і 150. 18.30. 1;
5
![]() 2; 4; 8. 18.31. Так, b1 = , q = 4. 18.32. x1 = 49, q = 7. 18.33. 1) 15 4
2; 4; 8. 18.31. Так, b1 = , q = 4. 18.32. x1 = 49, q = 7. 18.33. 1) 15 4
![]()
![]() або –15; 2) 6 або –6; 3) 2 5 або −2 5. 18.34. 2. 18.35. 2 або
або –15; 2) 6 або –6; 3) 2 5 або −2 5. 18.34. 2. 18.35. 2 або
![]() 3) Послідовність
3) Послідовність
є геометричною прогресією, якщо q ≠ –1. 18.43. 80, 40, 20, 10, 5 або 80, –40, 20, –10, 5. 18.44. 6, 18, 54, 162, 486 або 6, –18, 54,
![]()
![]()
![]() –162, 486. 18.45. 1) b1 = 2 3, q = 3 або b1 = −2 3, q = − 3;
–162, 486. 18.45. 1) b1 = 2 3, q = 3 або b1 = −2 3, q = − 3;
1
![]()
![]() 2) b1 = 162, q =; 3) b1 = 7, q = –2 або b1 =, q = –3. 18.46. 1) b1 =, 2 q = 4; 2) b1 = –1, q = 3. 18.47. При x = 1 маємо 3, 6, 12; при x = –14 маємо –27, –9, –3. 18.48. При x = 2 маємо 8, 4, 2; при x = –7 маємо –1, –5, –25. 18.50. 96, 48, 24, 12, 6, 3. 18.51. 3, 7, 11. 18.52. 8, 10, 12 або 17, 10, 3. 18.53. 5, 15, 45 або 45, 15, 5. 18.54. 2, 6, 18 або 18, 6, 2. 18.59. За 2 дні. 18.60. 6 кг, 18 кг або 9 кг, 21 кг.
2) b1 = 162, q =; 3) b1 = 7, q = –2 або b1 =, q = –3. 18.46. 1) b1 =, 2 q = 4; 2) b1 = –1, q = 3. 18.47. При x = 1 маємо 3, 6, 12; при x = –14 маємо –27, –9, –3. 18.48. При x = 2 маємо 8, 4, 2; при x = –7 маємо –1, –5, –25. 18.50. 96, 48, 24, 12, 6, 3. 18.51. 3, 7, 11. 18.52. 8, 10, 12 або 17, 10, 3. 18.53. 5, 15, 45 або 45, 15, 5. 18.54. 2, 6, 18 або 18, 6, 2. 18.59. За 2 дні. 18.60. 6 кг, 18 кг або 9 кг, 21 кг.
18.61. 3 кг. 18.62. 6 %. 18.63. 10 %.
19. Сума n перших членів геометричної прогресії
![]() 19.5. 1) 1456; 2) 155 (5 + 5 ). 19.6. 762. 19.7. 1210. 19.8. –68,2.
19.5. 1) 1456; 2) 155 (5 + 5 ). 19.6. 762. 19.7. 1210. 19.8. –68,2.
![]()
![]() 19.9. 27. 19.10. –7 або 6. 19.11. 5. 19.12. (272 – 1) бактерій. 19.13. 72. 89 −18; 13 ;
19.9. 27. 19.10. –7 або 6. 19.11. 5. 19.12. (272 – 1) бактерій. 19.13. 72. 89 −18; 13 ;
19.14. . 19.15. 4368. 19.16.–12 285. 19.19. 5. 19.20. 1) 7
2) [–1; 4). 19.23. 50 деталей, 40 деталей. 19.24. 1) b – 5a; 2) x + 2y.
19.25. На 10 % першого разу і на 20 % другого. 19.26. 20 %.
20. Вправи для повторення курсу алгебри 9 класу
![]() 20.17. 6. 20.24. 1) (1; +×); 2) [2; 3); 3) [–2; 16]; 4) (–4; 7]. 20.25. 1) –9; 2) –2. 20.27. 2. 20.29. 1) a < 4; 2) a < 2; 3) am−3; 4) al1. 20.30. 1) al 6; 2) al 5; 3) a > –8; 4) am 0. 20.32. a < –1,5 і a ≠ –2. 20.33. a = 0. 20.41. 1) b = 6, c = 9; 2) b = 0, c = 4; 3) b = –3, c = –10. 20.44. 3) −2 2 або
20.17. 6. 20.24. 1) (1; +×); 2) [2; 3); 3) [–2; 16]; 4) (–4; 7]. 20.25. 1) –9; 2) –2. 20.27. 2. 20.29. 1) a < 4; 2) a < 2; 3) am−3; 4) al1. 20.30. 1) al 6; 2) al 5; 3) a > –8; 4) am 0. 20.32. a < –1,5 і a ≠ –2. 20.33. a = 0. 20.41. 1) b = 6, c = 9; 2) b = 0, c = 4; 3) b = –3, c = –10. 20.44. 3) −2 2 або ![]() , b = –4, c = 10.
, b = –4, c = 10.
20.47. a = 2, b = –1, c = –3. 20.48. 1) 1; 2) –8. 20.50. 1. 20.51. 10 при a = 1 і b = 3. 20.54. При c > 0,1. 20.58. 1) a ≠ 4; 2) a![]() , або
, або ![]() < a < 1, або a > 13; 3) a < –1, або −
< a < 1, або a > 13; 3) a < –1, або −![]() < a < 0, або a > 0.
< a < 0, або a > 0.
20.59. 1) a > ![]() ; 2) a < –5; 3) am−1; 4) a >
; 2) a < –5; 3) am−1; 4) a > ![]() . 20.60. 1) (1; 4), (–2; 7);
. 20.60. 1) (1; 4), (–2; 7);
2) (3; –4), (4; –3); 3) (4; 0), (0; –4); 4) (0; –5), (3; 4), (–3; 4).
![]() 20.61. 1) (–2; 1), (–0,4; 1,4); 2) (–2; 4), 14; − 20 ; 3) (3; 5), (10; 1,5);
20.61. 1) (–2; 1), (–0,4; 1,4); 2) (–2; 4), 14; − 20 ; 3) (3; 5), (10; 1,5);
9 3
4) (4; –3), (2; –6); 5) (–5; 2); 6) (3; 2), (–2; –3); 7) (3; –2), (0; 1); 8) (1; –2), (3; 0); 9) (8; 4), (4; 8); 10) (1; 5), (–5; –1). 20.62. 1) (2; 1), (–2; –1), (1; 2), (–1; –2); 2) (5; 1), (1; 5), (2; 3), (3; 2); 3) (2; 1), (1; 2);
![]()
![]()
![]() 4) (6; 4), 4; − 6 ; 5) (4; 1), − 1; 5 1 , (–4; –1), 1; −5 1 ; 6) (3; –2),
4) (6; 4), 4; − 6 ; 5) (4; 1), − 1; 5 1 , (–4; –1), 1; −5 1 ; 6) (3; –2),
5 5 4 4 4 4
(–3; 2); 7) (10; 5), (–5; –10); 8) (5; 3), (5; –3), (–5; 3), (–5; –3);
![]() − 5; − 2 , (–1; –2),
− 5; − 2 , (–1; –2),
9) (3; 4), (4; 3), (–3; –4), (–4; –3); 10) (1; 2),
3 3
5 2
![]() ; . 20.63. 1) (3; 4), (4,5; 8,5); 2) (3; 1), (–1,5; –2); 3) (3; 2),
; . 20.63. 1) (3; 4), (4,5; 8,5); 2) (3; 1), (–1,5; –2); 3) (3; 2),
3 3
![]()
![]() (2; 3), (–3; –2), (–2; –3). 20.64. 1) a =
(2; 3), (–3; –2), (–2; –3). 20.64. 1) a = ![]() ; 2) a = 2 3 або a = −2 3. 20.65. 8 см, 15 см. 20.66. 9 см, 40 см. 20.67. 80 км/год, 60 км/год.
; 2) a = 2 3 або a = −2 3. 20.65. 8 см, 15 см. 20.66. 9 см, 40 см. 20.67. 80 км/год, 60 км/год.
20.68. 6 км/год, 4 км/год. 20.69. 12 км/год, 4 км/год. 20.70. 55 км/год, 75 км/год. 20.71. 2 год, 6 год. 20.72. 36 год, 12 год. 20.73. 0,5 км/год. 20.74. 15 км/год, 12 км/год. 20.75. 72 км/год, 48 км/год. 20.78. ![]() . 20.80. З тридцять другого по шістдесят четвертий. 20.83. 2,4 см, 3,2 см. 20.84. 6) Так, 2d;
. 20.80. З тридцять другого по шістдесят четвертий. 20.83. 2,4 см, 3,2 см. 20.84. 6) Так, 2d;
![]() 7) так, 4d. 20.85. 0, 4, 8. 20.88. 1) n a n( − ); 2) n na b( − ). 20.89. 11. a a b+
7) так, 4d. 20.85. 0, 4, 8. 20.88. 1) n a n( − ); 2) n na b( − ). 20.89. 11. a a b+
20.90. 1) a1 = –7, d = 3; 2) a1 = 5, d = –2 або a1 = 3, d = –2; 3) a1 =
= d = 3 або a1 = –33, d = 15; 4) a1 = –0,7, d = 0,3; 5) a1 = 0, d = 1,5.
2a2
20.91. 10. 20.92. 255. 20.93. ![]() . 20.94. 1160. 20.95. 2610. Вказів3
. 20.94. 1160. 20.95. 2610. Вказів3
ка. Шукана сума S = S1 – S2 – S3 + S4, де S1 — сума всіх двоцифрових чисел; S2 — сума двоцифрових чисел, які кратні 3; S3 — сума двоцифрових чисел, які кратні 5; S4 — сума двоцифрових чисел, які кратні 15. 20.96. Так, q = ![]() . 20.97. 20 %. 20.99. 2.
. 20.97. 20 %. 20.99. 2.
2 2 1
20.100. 2 ![]() , 4, 6, 9. 20.101. 3) Так, q ; 4) так, q; 5) ні; 6) так,
, 4, 6, 9. 20.101. 3) Так, q ; 4) так, q; 5) ні; 6) так, ![]() .
.
3 q
Для тих, хто хоче знати більше
21. Основні правила комбінаторики
21.1. 9 маршрутів. 21.2. 6 вариантів. 21.3. 15 вариантів.
21.4. 70. 21.5. 1) 8; 2) 4. 21.6. 4 . 3. 21.7. 3 . 6 . 5. 21.8. 1) 4 . 2; 2) 4 . 4. 21.9. 1) 6; 2) 2. 21.10. 100. 21.11. 20. 21.12. 25. 21.13. 8. 21.14. 63. 21.15. 16. 21.16. 32 . 24. 21.17. 9 . 10 . 10 . 10 . 5.
21.18. 9 . 10 . 10 . 10. 21.19. 11 . 9 +8 . 7. 21.20. 55 + 4 . 54.
23. Класичне означення ймовірності
23.20. 1) ![]() ; 2)
; 2) ![]() . 23.23. 10 куль. 23.24. 1)
. 23.23. 10 куль. 23.24. 1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() .
.
23.25. ![]() . 23.26.
. 23.26. ![]() . 23.27. 8 олівців. 23.28. 19 олівців. 23.30. 1)
. 23.27. 8 олівців. 23.28. 19 олівців. 23.30. 1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() . Вказівка. Сприятливі події позначено на рисунку зеленим кольором. 23.31. 1)
. Вказівка. Сприятливі події позначено на рисунку зеленим кольором. 23.31. 1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() . Вказівка. Кинути
. Вказівка. Кинути
кубик двічі — це те саме, що незалежно один від одного кинути два кубики. Далі скористайтеся рисунком 23.2. 23.32. У Петра.
До задачі 23.30
23.33. 1) ![]() ; 2)
; 2) ![]() . 23.34.
. 23.34. ![]() . 23.35. 1)
. 23.35. 1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]() . Вказів-
. Вказів-
ка. Кинути монету тричі — те саме, що незалежно одну від одної кинути три монети. Якщо пронумерувати монети, то маємо 8 рівноможливих результатів, як показано на рисунку.
|
Перша монета |
Друга монета |
Третя монета |
|
Г |
Г |
Г |
|
Г |
Г |
Ц |
|
Г |
Ц |
Г |
|
Г |
Ц |
Ц |
|
Ц |
Г |
Г |
|
Ц |
Г |
Ц |
|
Ц |
Ц |
Г |
|
Ц |
Ц |
Ц |
До задачі 23.35
2
23.36. ![]() . Вказівка. Якщо один зі знайомих сидить, то другий n− 1 може з однаковою ймовірністю сісти на одне з решти n – 1 місць.
. Вказівка. Якщо один зі знайомих сидить, то другий n− 1 може з однаковою ймовірністю сісти на одне з решти n – 1 місць.
23.37. ![]() . Вказівка. Кожному варіанту розстановки, у якому A стоїть попереду B, відповідає варіант, де їх поміняли місцями й A стоїть після B. Тому кількість сприятливих варіантів становить половину всіх варіантів.
. Вказівка. Кожному варіанту розстановки, у якому A стоїть попереду B, відповідає варіант, де їх поміняли місцями й A стоїть після B. Тому кількість сприятливих варіантів становить половину всіх варіантів.
Відповіді та вказівки до вправ оповідання «Сумування» рубрики «Коли зроблено уроки»
1. n n( +1) − +1 1 n . 2. n n( +1)2 + −1 1 n . 3. 1) 10 10( n −1) −n;
2 4 4 5æ 2 2 3æ 9
50 10( n −1) 5n n−1 n n( +2) 1
2) − . 5. 1) ; 2) ; 3) 1− . Вказівка.
81 9 4n−3 n+1 (n+1)!
n 1 1 1 2n+1 1 1
= − ; 4) 1− 2 . Вказівка. 2 +1)2 =n2 − (n+1)2 .
(n+1)! n! (n+1)! (n+1) n n(
6. 1) n ; 2) n n( 2 + +2n 3). Вказівка. n n3 + +2 1 = −1 1 +n.
2(5n+2) 2(n+1) n n( +1) n n+1
7. 12 1+ −12 n1+1 −n1+2 . Вказівка. (n 12 = 1 n n1 − 1+2 . 8. 4 (nn n+(1) (+n3)+2).
+ −1) 1 2
![]() Вказівка. n n( +11) (n+2) = 1 æ1 n n1 − 1+2 = 12 n n( 1+1) − (n+1) (1n+2) . n+1 2
Вказівка. n n( +11) (n+2) = 1 æ1 n n1 − 1+2 = 12 n n( 1+1) − (n+1) (1n+2) . n+1 2
9. Sn = na−1− (aan−−11)2. Вказівка. Розгляньте рівність aSn = +a 2a2 + 3a3 + n a
+4a4 + ... +n aæ n.
Відповіді до завдань «Перевірте себе» в тестовій формі
|
Номер завдання |
|
|
|
|
|
Номер задачі |
||||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
|
|
1 |
Б |
Г |
Б |
В |
Б |
А |
В |
В |
В |
А |
Б |
Г |
Г |
А |
Г |
В |
Б |
Б |
|
2 |
Г |
В |
Б |
В |
А |
Г |
Г |
В |
В |
В |
В |
Г |
Б |
Г |
Б |
В |
В |
А |
|
3 |
В |
Б |
А |
В |
Г |
А |
А |
В |
В |
А |
Г |
Б |
Г |
В |
Г |
А |
Г |
Б |
|
4 |
Б |
В |
Б |
Г |
Г |
В |
А |
Б |
Б |
В |
Б |
А |
А |
Г |
В |
Б |
А |
В |
Предметний покажчик
Аргумент функції 59
Властивості числових нерівностей 12
Графічний метод розв’язування нерівностей 118
Доведення нерівностей 6
Знаки нерівності 6
Знаменник геометричної прогресії 173
Значення функції 60
Математична модель 138 Математичне моделювання 138
Межі значення величини 19
Метод додавання 129
— заміни змінних 130
— підстановки 128
Множина розв’язків нерівності 28
— — системи нерівностей 42
Нерівність лінійна з однією змінною 35
— нестрога 6
— строга 6
Нерівності квадратні 118
— однакового знака 18
— протилежних знаків 18
— рівносильні 29
— числові 5
Нуль функції 69
Об’єднання проміжків 118
Область визначення виразу 42
— — функції 59
— значень функції 60
Оцінювання значення виразу 19
Парабола 77
Переріз проміжків 43
Порівняння чисел 5
Порожня множина 28
Послідовність 151
— нескінченна 152
— скінченна 152
— числова 151
Початкові умови 153
Прикладна задача 138
Прогресія арифметична 160
— геометрична 173
Проміжок знакосталості функції 69
— зростання функції 70
— спадання функції 70 Процентні пункти 184
Різниця арифметичної прогресії 160
Розв’язок нерівності з однією змінною 28
— системи нерівностей з од- нією змінною 42
Середнє геометричне 7
Система нерівностей 42
|
Предметний покажчик |
Спосіб задання послідовності описовий 152
— — — рекурентний 153
— — функції аналітичний 60
Сумування перших n членів послідовності 190
Формула рекурентна 153
— складних відсотків 178
— суми n перших членів арифметичної прогресії 167
— — — — — геометричної прогресії 186
— n-го члена арифметичної прогресії 161
— — — геометричної прогресії 175
— — — послідовності 152
Функція 59
— зростаюча 70
— — на проміжку 70
— квадратична 98
— спадна 70
— — на проміжку 70
Числова пряма 34
Числовий проміжок 32
Член послідовності 151
ЗМіСт
Від авторів ........................................................................3
Умовні позначення .............................................................4
§ 1. нерівності ......................................................................5
1. Числові нерівності ...................................................5 2. Основні властивості числових нерівностей .................12
3. Додавання і множення числових нерівностей.
Оцінювання значення виразу ................................. 17
• Про деякі способи доведення нерівностей ..................24
4. Нерівності з однією змінною ....................................28
5. Розв’язування лінійних нерівностей з однією змінною. Числові проміжки ................................... 31 6. Системи лінійних нерівностей з однією змінною ........42
Завдання № 1 «Перевірте себе» в тестовій формі ................54
Головне в параграфі 1 ........................................................ 57
§ 2. квадратична функція ................................................... 59
7. Повторення та розширення відомостей про функцію ... 59 • З історії розвитку поняття функції .......................... 65
8. Властивості функції ................................................68
9. Як побудувати графік функції y = k f (x), якщо відомо графік функції y = f (x) ...................... 77
10. Як побудувати графіки функцій y = f (x) + b і y = f (x + a), якщо відомо графік функції y = f (x) ....85
11. Квадратична функція, її графік і властивості ......... 98
• Про деякі перетворення графіків функцій ................109
Зміст
• Як побудувати графік функції y = f (–x), якщо відомо графік функції y = f (x) .....................109
• Як побудувати графік функції y = f (| x |), якщо відомо графік функції y = f (x) .....................110
• Як побудувати графік функції y = | f (x) |, якщо відомо графік функції y = f (x) .....................111
Завдання № 2 «Перевірте себе» в тестовій формі ..............115
12. Розв’язування квадратних нерівностей .................118
13. Системи рівнянь із двома змінними ......................127
• Перша Всеукраїнська олімпіада юних математиків ...136
14. Система двох рівнянь із двома змінними як математична модель прикладної задачі .............138 Завдання № 3 «Перевірте себе» в тестовій формі ..............146
Головне в параграфі 2 .......................................................149
§ 3. Числові послідовності ..................................................151
15. Числові послідовності ..........................................151
• Про кролів, соняшники, соснові шишки
та золотий переріз ...............................................157
16. Арифметична прогресія .......................................159
17. Сума n перших членів арифметичної прогресії ......166 18. Геометрична прогресія ........................................173
• Як уникнути неоднозначності в задачах
на відсоткові розрахунки .....................................184
19. Сума n перших членів геометричної прогресії .......185
• Сумування ............................................................190
Завдання № 4 «Перевірте себе» в тестовій формі ..............194
Головне в параграфі 3 .......................................................196
20. Вправи для повторення курсу алгебри 9 класу .......198
Зміст
для тих, хто хоче знати більше
21. Основні правила комбінаторики ...........................212
22. Частота та ймовірність випадкової події ................216
23. Класичне означення ймовірності ..........................224 • Спочатку була гра .................................................233
24. Початкові відомості про статистику ......................235
Дружимо з комп’ютером ...................................................248
Відповіді та вказівки до вправ ..........................................253
Відповіді до завдань «Перевірте себе» в тестовій формі ......266
Предметний покажчик .....................................................267
Видано за рахунок державних коштів. Продаж заборонено
Навчальне видання
МЕРЗЛЯК Аркадій Григорович
ПОЛОНСьКиЙ Віталій Борисович
ЯКІР Михайло Семенович
АЛГЕБРА
підручник для 9 класу
загальноосвітніх навчальних закладів
Рекомендовано
Міністерством освіти і науки України
Головний редактор Г. Ф. Висоцька
Відповідальний за випуск Д. В. Москаленко
Літературний редактор Т. Є. Цента
Художнє оформлення та дизайн Д. В. Висоцький
Технічний редактор О. В. Гулькевич Коректор Т. Є. Цента
Комп’ютерне верстання C. І. Северин
Формат 60![]() 90/16. Папір офсетний. Гарнітура шкільна.
90/16. Папір офсетний. Гарнітура шкільна.
Друк офсетний. Ум. друк. арк. 17,00. Обл.-вид. арк. 13,46. Тираж 184 221 прим. Замовлення №
ТОВ ТО «Гімназія», вул. Восьмого Березня, 31, м. Харків 61052
Тел.: (057) 719-17-26, (057) 719-46-80, факс: (057) 758-83-93
E-mail: contаct@gymnasia.com.ua www.gymnasia.com.ua
Свідоцтво суб’єкта видавничої справи ДК № 644 від 25.10.2001
Надруковано з діапозитивів, виготовлених ТОВ ТО «Гімназія», у друкарні ПП «Модем»,
вул. Восьмого Березня, 31, м. Харків 61052 Тел. (057) 758-15-80
Свідоцтво суб’єкта видавничої справи ХК № 91 від 25.12.2003
[1] Пізніше на уроках геометрії ви більш докладно ознайомитеся з паралельним перенесенням.
[2] Формулу y0 = − запам’ятовувати необов’язково. Достатньо об4a
[3] b числити значення функції y = ax + bx + c у точці з абсцисою x0 = − ![]() .
.
2a
[4] На уроках геометрії ви дізнаєтеся, що описане перетворення графіка функції y = f (x) називають осьовою симетрією.
[5] У ботаніці таке сполучення двох сімейств спіралей називають філотаксисом.
[6] Парфенон — храм в Афінах, побудований у V ст. до н. е.
[7] Безуˊ Етьєн (1730–1783) — французький математик, основні роботи якого стосуються вищої алгебри. Викладав математику в училищі гардемаринів, Королівському артилерійському корпусі. Автор шеститомної праці «Курс математики».
[8] Гіпсикл Александрійський (ІІ ст. до н. е.) — давньогрецький учений, автор ХІV книги «Начал» Евкліда.
[9] Називатимемо цю властивість «принципом незалежності кількості виборів».
[10] Демографія — наука про народонаселення.
[11] Т. Г. Шевченко. Твори у 12 т. Інститут літератури ім. Т. Г. Шевченка Академії наук України. — К. : Наукова думка, 2003. — Т. 2. — С. 17.


про публікацію авторської розробки
Додати розробку