Урок "Декартова система координат", 9 клас

Урок у 9 класі

Тема:   Декартова система координат

Мета:   повторити, узагальнити і систематизувати знання декартової системи координат, формул для знаходження відстані між точками, координат середини відрізка, рівняння кола та прямої, продовжувати формувати навички розв’язувати задачі на застосування формул та рівнянь цієї теми. Розвивати здібності учнів, творчу активність, ініціативу, правильність і чіткість мови, виховувати почуття колективізму, взаємодопомоги.

Тип уроку: узагальнення й систематизація знань та умінь

Обладнання: монітор, магнітна дошка, презентації, конспект.

Мало мати хороший розум,

головне – добре його застосовувати.

Рене Декарт

Хід уроку

1.      Організаційна частина

    Відомий французький письменник ХІХ ст.. Анатоль Франс одного разу зауважив: «Навчатися можна тільки весело… Щоб перетравлювати знання, потрібно поглинати їх з апетитом.» Ці слова ми візьмемо за девіз нашого уроку, на якому ми не просто будемо повторювати вивчений матеріал, але й, сподіваюсь, цікаво проведемо час. Нас чекає багато роботи, але це не має завадити нашому гарному настрою.

  Перед кожним із вас лежить персональна картка, у яку протягом уроку вноситимуться зароблені вами бали. Бажаю вам накопичити достатню кількість балів, щоб у кінці уроку претендувати на високу оцінку!

   Для розминки проведемо гру «Мікрофон»:

 "Не існує не талановитих людей,а є ті…"

Завдання:запропонуйте свій варіант відповіді.

(Відповідь:…які займаються не своєю справою)

Можливо,цей урок геометрії стане тією справою,яка дасть змогу кожному з вас розкрити свої таланти. Будьте активними,наполегливими,кмітливими!

II. Повідомлення теми та мети уроку

III. Актуалізація опорних знань учнів

    1. Актуалізація опорних знань проводиться з допомогою презентації

Усні відповіді на запитання:(за правильну відповідь - 2 бали)

1.     Що таке координатна площина? (Це площина із зведеною на ній системою координат).
2.     Як визначити координати точки? (Треба через дану точку провести дві прямі, паралельні осям координат, на координатних осях відмітити числа, які відповідають точкам перетину цих прямих з осями)
3.     Як знайти відстань між двома точками із заданими координатами? (записати на дошці формулу).
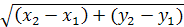4.     Як знайти координати середини відрізка? (записати на дошці , )
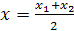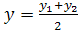5.     Що називається радіусом кола? (відрізок, що сполучає центр кола з будь-якою точкою на колі)
6.     Яким рівнянням задається коло?

(записати на дошці )

7.     Записати вигляд рівняння кола з центром в початку координат? (записати на дошці )
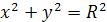8.     Запишіть загальний вигляд рівняння прямої? (на дошці записати

)

9.     Яке рівняння прямої з кутовим коефіцієнтом; що проходить через дві точки? (записати на дошці  )

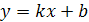2. Продовжте речення.

Продовжте речення. (Запитання висвітлюються на екрані)

1.     Якщо точки лежать на осі ординат, то … (x=0)
2.     Якщо точки лежать на осі абсцис, то … (y=0)
3.     Якщо координати точки додатні, то … (точка знаходиться в першій чверті)
4.     Якщо координати точки від’ємні, то … (точка знаходиться в третій чверті)
5.     Якщо абсциса точки від’ємна, а ордината додатна, то … (точка знаходиться в другій чверті)
6.     Якщо точки мають рівні абсциси, то … (вони лежать на одній прямій, яка паралельна осі y)
7.     Якщо точки мають рівні ординати, то … (вони лежать на одній прямій, яка паралельна осі x)
8.     Якщо абсциса й ордината точки дорівнюють нулю, то … (точка лежить в початку координат)

Учні дописують відповідь, міняються зошитами і перевіряють роботу сусіда. Відповіді на комп’ютері. Кожне завдання 0,5 бала.

3. Розв'язування задач за готовим малюнком (малюнки висвітлюються на екрані)

1.   Визначте координати  наступних точок.  Усно!!!

         A(-3, 1)   B(2, 3  )   C(1, -2)     D(-6, -2)

2. Знайти відстань між точками. Письмово на дошці!!!

          A(-3, 4)  B(5, -2)      Відповідь   -  d=10

3.     Знайти координати середини відрізка. Письмово на дошці.

        M(-3, -2)  N(-1, 4)      Відповідь –   (-2, 1)

4.     Знаючи координати початку і середини відрізка, знайти координати кінця. Письмово на дошці

          C(-2,-3)  E(-1, -2)    Відповідь – F(-3, -4)

5.     Скласти рівняння кола за малюнком. Письмово на дошці.

6.     Скласти рівняння прямої, що проходить через дві точки. Письмово на дошці.

        (-3, 1)  (2, -2)   Відповідь –

Малюнки відображаються на екрані, і до кожного малюнка готові відповіді. Учні записують в зошитах, а хтось один на дошці.

4. Робота біля дошки (задача про квадрат)

Задача: Знайти координати двох інших вершин квадрата ABCD. Скільки розв’язків має задача. (Малюнок даємо одному учневі, який малює, що дано і зразу розв’язує задачу)

Вчитель запитує, скільки розв’язків має задача

5.   Робота коригувальника (5 задач)

Учні знаходять помилку у рівнянні і малюнку. На екрані висвітлюється спочатку неправильно, а потім правильно.

1.

2.

3.

4.

5.

6. Робота з підручником  №330. Знайдіть точку перетину прямих:

а) 3x+ y+ 5 = 0 і х-2у-3 = 0;

         №331. Знайдіть точки перетину:

а) прямої х-3у + 6 = 0 і кола (х - 2)2 + (у- І)2 = 25;

Учень йде  до дошки і розв’язує задачу

7.     Самостійна робота із наступною перевіркою

(Додатково, якщо залишиться час).

Дано коло (х-4)²+(у+1)²=25

1. Радіус кола дорівнює..., а координати центра...
2. Коло перетинає вісь у в точках, координати яких можна знайти так...
3. Точки М(0;2) і К(4;4) лежать на даному колі, тому що...
4. Координати середини відрізка МК такі... Ця точка не належить колу тому що...
5. З точок А(0;-3), В(1;1), С(-2;6), D(2;0) на прямій 3х+2у-6=0 лежать...
6. З прямих х-2у+1=0; 3х+у+1=0;у-2=0 через точку Е(-1;2) проходять...
7. 3 графіків рівнянь у=-3х, у=3/х, у=3-х, у=3х² прямими лініями є... З цих прямих через початок координат проходять...
8. Рівняння прямої, яка проходить через точку М(3;4) і паралельна осі у, таке…

VI. Оцінювання учнів

Учням надається час для підрахунку балів, отриманих протягом уроку. Учні по черзі оголошують отримані бали; оцінки, при бажанні учнів, виставляються в журнал

VII. Домашнє завдання (в залежності від отриманих балів)

Для тих, хто отримав "6" і менше:

№319. Складіть рівняння прямої, яка проходить через початок коор-динат і центр кола, заданого рівнянням (х + З)2 + (у - З)2 = 1. Визначте, які з точок .А(-1; -1), В(-8; 8), С(12; 12) лежать на цій прямій.

№322. Знайдіть точку перетину прямих 2х - у - 9 = 0 і у = -х.

Для тих, хто отримав "7" і більше:

№ 329. Складіть рівняння прямих, що містять сторони трикутника ABC, якщо А(-1; -1), В(-1; 3), С(2; 2)

№332. Дано коло (х - З)2 + (у - 2)2 = 8 і прямі x-y + 3 = 0 та х + у- 9 = 0. Знайдіть точку   

перетину даних прямих і спільні точки кожної з них і кола.

VIII. Підсумок уроку

     Сьогодні ми розібралися з дуже важливим питанням — розташуванням прямих у просторі. Усі просторові геометричні фігури, з якими ви познайомитеся пізніше, можна побудувати за допомогою прямих. Знання властивостей, якими вони пов'язані, дають змогу розв'язати багато важливих задач, серед яких більшість прикладного характеру.

Аналіз емоційного стану.

З використанням обличчя та сходів

«Обличчя» роздаються кожному з учнів перед початком уроку. При підведенні підсумків учні розташовують його або «радісним», або «сумним» на сходинку, яку вважають відповідною своєму рівню. Рівні: я знаю, я вмію, все можу                        

 Все зможу

                                            Я вмію

              Я знаю