Картка заняття "Аналітичні методи розв’язування планіметричних задач. Обчислення площ геометричних фігур"

НАВЧАЛЬНО – МЕТОДИЧНА КАРТКА  ЗАНЯТТЯ  № 54

Предмет: Математика

                                 (назва)

Тема заняття: Аналітичні методи розв’язування планіметричних задач. Обчислення площ геометричних фігур.

Вид заняття(тип лекції): Комбіноване заняття (формування та вдосконалення вмінь і навичок)

_________________________________________Час__80 хв.___

Забезпечення заняття  _________54______________

 (шифр картки)

А. Засоби наочності : презентація.

Б.Роздатковий матеріал: кросворд.

В.Технічні засоби навчання :ноутбук, проектор з мультимедійною дошкою

Г.Навчальні місця (для практ. занять, лаб. робіт) 32 робочі місця

Д. Література:

Основна:

1. Погорєлов О.В. Геометрія: Підруч. для 10-11 кл. загальноосвітніх навчальних закладів – К.: Школяр, 2004, Освіта, 2001

2.          Бевз Г.П. та інші. Геометрія: Підручник для шкіл з поглибленим вивченням математики, 10-11 кл. – К.: Освіта, 2000, 2005

Додаткова :

1. Афанасьєва О.М., Бродський Я.С., Павлов О.Л., Сліпенько А.К. Математика (підручник для студентів ВНЗ І-ІІ р.а. технічних спеціальностей) – К.: Вища школа, 2001

1. Підготовка групи до навчання

• Перевірка присутності студентів.

• Виявлення рівня підготовки студентів з точки зору оснащення.

• Вступне слово викладача.

2. Повідомлення теми, мети заняття
3. Актуалізація опорних знань і контроль вихідного рівня знань студентів

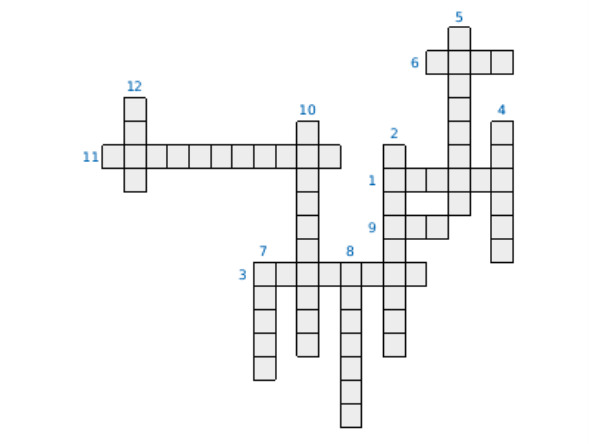
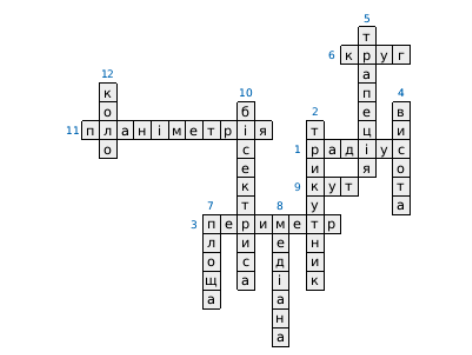
1. Відрізок, що сполучає точку на колі з його центром.
2. Геометрична фігура, що складаться з трьох точок і трьох відрізків.
3. Сума сторін многокутника.
4. Відрізок,що виходить з вершини кута і перпендикулярний до протилежної сторони.
5. Чотирикутник у якого дві протилежні сторони паралельні,а дві інші не паралельні.
6. Геометричне місце точок на площині що знаходяться від даної точки на відстані, що не перевищує задану.
7. В прямокутному трикутнику дорівнює півдобутку катетів.
8. Відрізок,що виходить з вершини кута і ділить протилежну сторону навпіл.
9. Геометрична фігура, що складається з точки і двох променів, які виходять з неї.
10. Відрізок,що виходить з вершини кута і ділить його навпіл.
11. Розділ геометрії, що вивчає геометричні фігури на площині.
12. Геометричне місце точок на площині рівновіддалених від даної точки.

4. Мотивація навчальної діяльності студента

Рене Декарт сказав: «Я мислю, отже я існую». Ніяка інша наука так не вчить мислити, як геометрія.

5. План заняття

• Повторення методів розв’язування задач з планіметрії

• Розв’язування планіметричних задач

•  Опитування

6. Повторення та систематизація вмінь

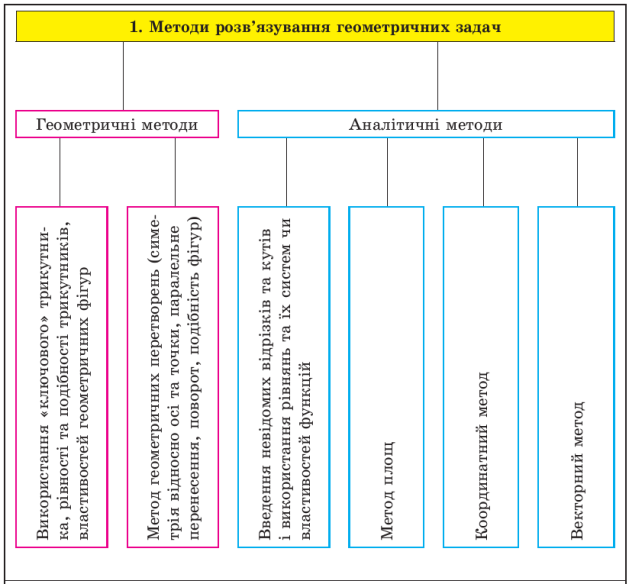
Геометричні задачі за змістом можна умовно поділити на такі основні види: задачі на доведення, обчислення, побудову. Методи розв'язування задач можна поділити на геометричні й аналітичні.

Аналітичні методи передбачають застосування тотожних перетворень і співвідношень, отриманих на підставі відомих геометричних фактів. Такі перетворення, формули часто застосовуються без урахування взаємного розміщення фігур і їхніх елементів. Розв'язати задачі, використовуючи аналітичний метод, досить часто можна без побудови рисунка.

Геометричні методи ґрунтуються на застосуванні властивостей, ознак фігур і співвідношень між ними. У цьому випадку обґрунтування задачі пов'язане із взаємним розміщенням самих фігур або їхніх елементів і тому супроводжується рисунком.

Іноді при розв'язуванні задач доводиться застосовувати кілька методів або ту саму задачу можна розглядати беручи до уваги різні методи.

7. Узагальнення та систематизація вивченого матеріалу, здобутих вмінь і навичок

Задача 1. У рівнобедреному трикутнику медіана, проведена до основи, дорівнює 25 см. Обчисліть площу цього трикутника, якщо радіус вписаного в нього кола дорівнює 10 см.

Задача 2. Дві сторони трикутника відносяться як 3:5, а кут між ними дорівнює 120⁰. Знайдіть всі сторони та площу трикутника, якщо його периметр дорівнює 15 см.

Розв’язування:

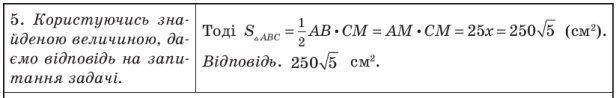
Задача 2.

8. Підведення підсумків заняття

1. Які є методи розв’язування задач з планіметрії? (Геометричні та аналітичні)
2. В чому полягає суть аналітичного методу? (Розв’язування геометричних задач засобами алгебри, інколи навіть без використання рисунку)
3. Чи завжди задача розв’язується тільки одним способом та одним методом? (Ні)
4. За словами Рене Декарта, коли ми існуємо? (Коли ми мислимо)

9. Постановка домашнього завдання

Одна сторона трикутника дорівнює 35 см, а дві інші відносяться як 3:8 і утворюють кут 60 ⁰. Знайдіть невідомі сторони, периметр та площу трикутника.

Студента(ки)____________________________________________

1. Відрізок, що сполучає точку на колі з його центром.
2. Геометрична фігура, що складаться з трьох точок і трьох відрізків.
3. Сума сторін многокутника.
4. Відрізок,що виходить з вершини кута і перпендикулярний до протилежної сторони.
5. Чотирикутник у якого дві протилежні сторони паралельні,а дві інші не паралельні.
6. Геометричне місце точок на площині що знаходяться від даної точки на відстані, що не перевищує задану.
7. В прямокутному трикутнику дорівнює півдобутку катетів.
8. Відрізок,що виходить з вершини кута і ділить протилежну сторону навпіл.
9. Геометрична фігура, що складається з точки і двох променів, які виходять з неї.
10. Відрізок,що виходить з вершини кута і ділить його навпіл.
11. Розділ геометрії, що вивчає геометричні фігури на площині.
12. Геометричне місце точок на площині рівновіддалених від даної точки.

Оцінка ____________________ Перевірив ______________________________