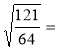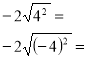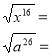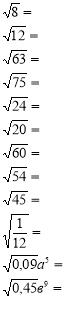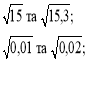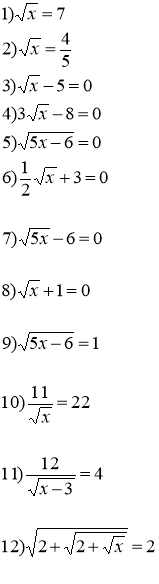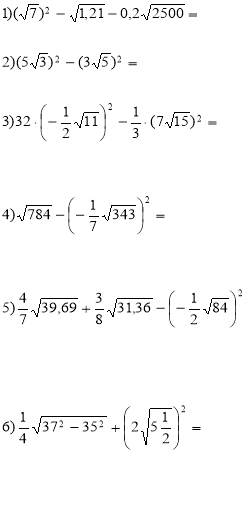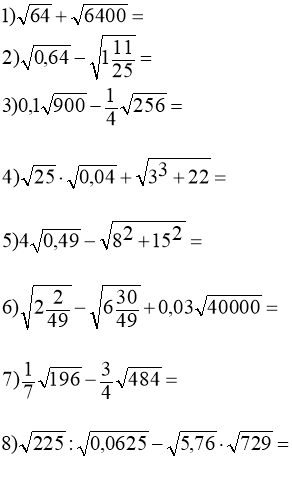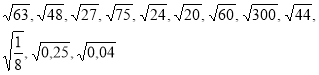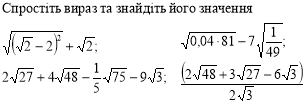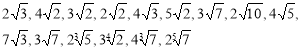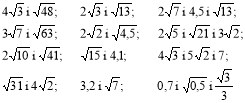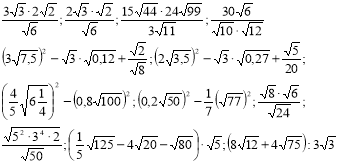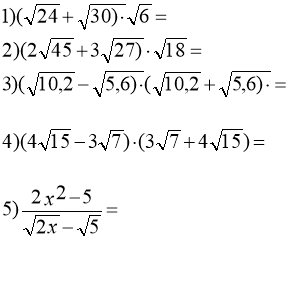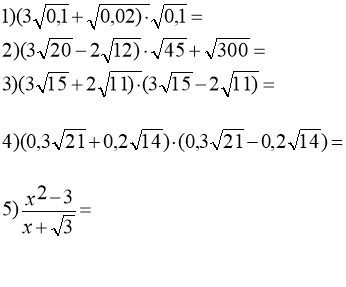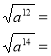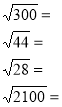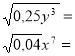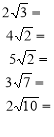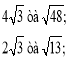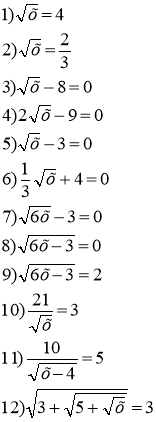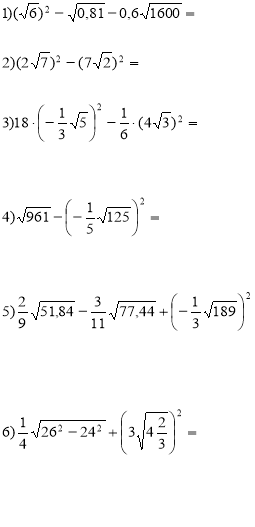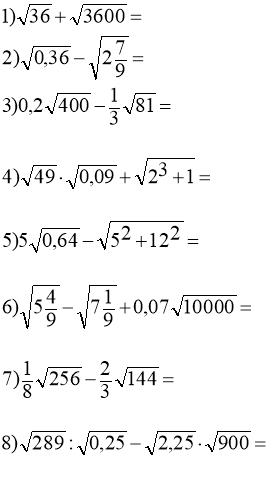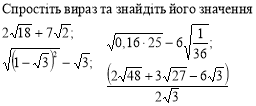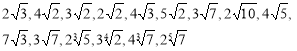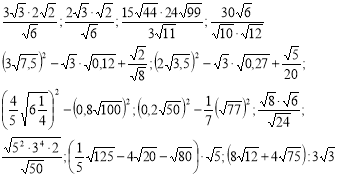Картки диференційованого контролю знань з теми «Арифметичний квадратний корінь»

Властивості кореня

1.

Приклад:

Свій приклад:

2.    

 Приклад:

Свій приклад:

3.

 Свій приклад:

4.

Приклад:

Свої приклади:

5.

Свої приклади:

Рівняння виду х² = а

1. х² = 100;
2. х² = 0,25
3. х² = - 16
4. х² = 13
5. 3х² = 0,48

6. х² - 49 = 0

8. (3х – 2)(3х + 2) = 5

9. (3х – 2)(3х + 2) = 0

10.   (х + 1)² = 64

11.   (4х – 9)² = 49

12.   (х - 3)² = 3

Винесення множника з-під знака кореня

Внесення множника під знак кореня

Порівняйте числа:

Рівняння √х = у

Перевір себе: я) ± 0,4;    е)  ± 1

Перевір себе: с) 49; п) 25; ь) 4;  и) 8; н) 7,2; у) 0,64; ц)12; е); в) 1,4; е) 0,25; ш) 9; з) немає кор.; а) немає кор.; р)1,2.

Властивість кореня  (√а)² = а, де а≥0

1.Знайдіть значення виразу:

Тотожні перетворення виразів, що містять квадратні корені

Середній рівень

Обчисліть:

Узагальнення знань про квадратний корінь

Середній рівень

Достатній  рівень

Високий рівень

Достатній  рівень

Внесіть множник під знак кореня

Високий рівень

Порівняйте числа

Спростіть вираз та, якщо можливо, обрахуйте його значення:

Перевір себе:

Перевір себе:  м) 88; н) ;  і) - 0,4; ч) ; й) - 1; п) -2; в) – 5; п) и) 5,1; у) 8; и) – 6; с) – 14,2; і) – 14,5; х) – 4,8.

Тотожні перетворення виразів, що містять квадратні корені В.І

Достатній та високий рівень

Зашифруйте відповідь:

Тотожні перетворення виразів, що містять квадратні корені. В ІІ

Достатній та високий рівень

Зашифруйте відповідь:

Властивості кореня

1.

Приклад:

Свій приклад:

2.       

Приклад:

Свій приклад:

3.

 Свій приклад:

4.

Приклад: 

Свій приклад:

5.

Свої приклади:

Рівняння виду х² = а

1. х² = 4;
2. х² = 0,09
3. х² = - 9
4. х² = 17
5. 2х² = 0,08

6. х² - 9 = 0

8. (2х – 5)(2х + 5) = 75

9. (2х – 5)(2х + 5) = 0

10.   (х – 9)² = 49

11.   (3х – 7)² = 121

12.   (х + 5)² = 2

Перевір себе: м) ± 0,2;    і)  ± 3

Винесення множника з-під знака кореня:

Внесення множника під знак кореня:

Порівняйте числа:

Рівняння √х = у

Перевір себе:  а) 2; ь) 961; с) 4; 

ц) 8; е) 49; і) 0,5; л); е); у); с) 16; п) 64; р) 9; у) немає кор.; ж) -144; м) 1,5.

Властивість кореня  (√а)² = а, де а≥0

1.Знайдіть значення виразу:

Тотожні перетворення виразів, що містять квадратні корені

Обчисліть:

Узагальнення знань про квадратний корінь

I рівень

II рівень

III рівень

Внесіть множник під знак кореня

Порівняйте числа

Спростіть вираз та, якщо можливо, обрахуйте його значення:

Перевір себе «Зашифруй відповідь»:

Перевір себе: м) 12; н) 66; е) а); у) 37; в) 1; с) 2,4; в) – 5; п) ч) 5,1; и) - 9; в) ; с) – 6; о) – 9;

я) – 11.