Кейс-урок "Світ симетрії "

Світ симетрії

 

Симетрія є тією ідеєю, за допомогою якої

людина протягом століть намагалася зрозуміти

і створити порядок, красу і досконалість.

Г.Вейль

 

Розділ:

 

Рівень: 8-11 клас

Тема: Природні явища

Мета: Дізнатися що таке симетрія в математиці, оточуючому світі, які види       симетрії існують і як закони симетрії впливають на наше життя

 

Яка інформація мене тут чекає:

 

• Що таке симетрія в математиці і світі
• Яку симетрію ми розглядаємо на уроках математики
• Чи є симетрія у фізиці та астрономії
• У чому гармонія природи
• Які види симетрії ми зустрічаємо у природі, архітектурі, живопису

 

6 розгорток  з предметів

 

 

                                                                     

 

 

З симетрією ми зустрічаємося будь-де: у природі, техніці, мистецтві, науці. Поняття симетрії проходить через усю історію людської творчості. Симетрія відіграє важливу роль в фізиці і математиці, хімії і біології, архітектурі, живопису і скульптурі, поезії і музиці. Закони природи підкоряються принципам симетрії. Чому симетрія присутня у середовищі, що нас оточує? Дивно, але симетрія пронизує наш світ набагато глибше, ніж ми можемо побачити це очима. Симетрія - що це?

 

 

Симетрія, як і гармонія, (з грецької) - відповідність, пропорційність, подібність в розташуванні частин, наявність порядку. У математиці вивчаються три види симетрії:

• центральна симетрія (симетрія відносно точки),

 

 

 

 

 

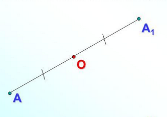
Якщо О - середина відрізка АА₁, то точки А і  А₁ симетричні відносно точки О, точка О центр симетрії. Така симетрія називається центральною.

Як побудувати фігуру, симетричну трикутнику АВС відносно точки О?

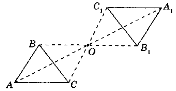                                                                                    О – середина  АА₁

                                                                                                                                   О – середина  СС₁

                                                                                    О – середина ВВ₁

 

Трикутник А₁В₁С₁ симетричний трикутнику АВС відносно точки О.

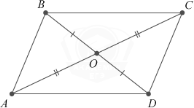Якщо симетрія відносно точки О переводить фігуру F у себе, то фігура F називається центрально-симетричною, О – центр симетрії. Прикладом центральносиметричної фігури відносно точки перетину діагоналей є паралелограм. Доведіть це.

 

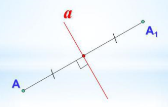• осьова симетрія (симетрія відносно прямої),

Якщо пряма а – серединний перпендикуляр до відрізка АА₁, то точки А і А₁ симетричні відносно прямої  а, а – вісь  симетрії.

 

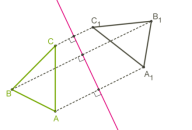Як побудувати фігуру, симетричну трикутнику АВС відносно осі а?                                                                                                                  

     а                                                                А  А₁,    

                                                                                   В  В₁,  

                                    С  С₁,

                                    ∆ АВС  ∆ А₁В₁С₁

 

 

• дзеркальна симетрія (симетрія відносно площини).

 

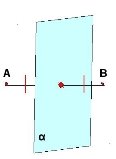
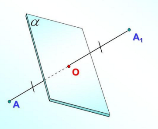
Поняття перетворення фігур у просторі означають так само як і на площині. У просторі розглядають симетрію відносно площини. Якщо площина α перпендикулярна до відрізка АВ, проходить через його середину, то точки А і В симетричні відносно площини α.

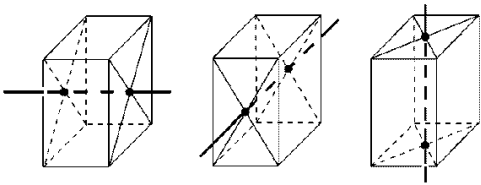
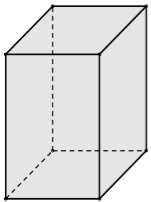
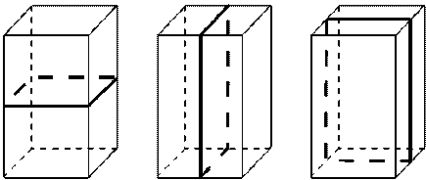
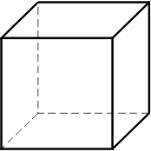
Розглянемо прямокутний паралелепіпед. Чи є в ньому центр симетрії, осі симетрії, площини симетрії?

 

 

 

 

 

 

У своїх міркуваннях про картину всесвіту людина з давніх часів використовувала ідею симетрії. Ще з часів давніх греків було встановлено, що існує всього п’ять правильних опуклих многогранників різної форми. Вперше їх дослідили піфагорійці, але описані докладно вони були Платоном і одержали назву платонових тіл (куб, правильний тетраедр, октаедр, додекаедр, ікосаедр).

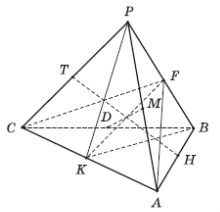
Характер симетрії правильного тетраедра зображено на малюнку.

Тетраедр має чотири поворотні осі третього порядку  (кожна вісь проходить через вершину тетраедра і центр протилежної грані) і три поворотні осі другого порядку (кожна проходить через середини протилежних ребер). Скільки площин симетрії має правильний тетраедер?

 

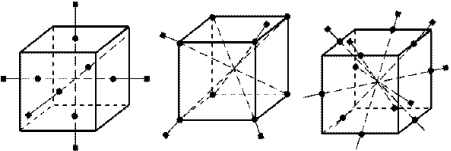
 Знайдіть у куба 13 поворотних осей симетрії.

 

 

 

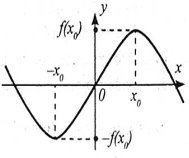
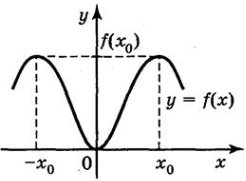
Яка симетрія має місце у розташуванні графіків парної функції, непарної функції?

 

 

Завдання:

1. Дано куб. Побудуйте фігуру, симетричну кубу відносно однієї з його вершин.

2. Які з букв А, Б, В, Г, Д, Е, К, М, П, Н, Ш мають вісь симетрії?

 

 

Симетрія в живих організмах була сформована в процесі еволюції. Усе живе в природі має властивості симетрії. Зовнішні форми людини і багатьох тварин мають досить симетричний вигляд, а симетричне розташування частин тіла забезпечує рівновагу при русі, адаптацію, життєстійкість. Природа - дивовижний творець. Нас вражає неповторність і чаруюча краса світу, що нас оточує. Із захватом слідкуємо ми за політом яскравих барвистих метеликів  і птахів, їх симетрією.

 

 

 

 

 

 

Жива природа дарує нам радість, захоплює своєю фантазією. Листя, квіти, плоди мають ярко виражену симетрію.

 

 

 

 

 

Багато квітів мають цікаву властивість: квітку можна повернути так, що кожен пелюсток займає положення сусіднього, квітка суміщається сама з собою. Така квітка має поворотну симетрію. Найменший кут, на який можна повернути квітку навколо осі симетрії, щоб вона співпала з собою, називається елементарним кутом повороту осі. Цей кут є різним, для іриса він дорівнює 120 градусів, для дзвоника 72 градуси, для нарциса 60. Квіти іриса, дзвоника, нарциса мають осі третього, п’ятого і шостого порядків відповідно. Особливо часто серед квітів зустрічається симетрія п’ятого порядку. Поворотна симетрія квітів існує разом з дзеркальною симетрією.

 

 

 

 

 

 

В просторі існують тіла, що мають гвинтову симетрію, тобто суміщаються зі своїм початковим положенням після повороту на деякий кут навколо осі, та ще й зсуваються вздовж цієї осі. Гвинтова симетрія має місце в розташуванні листів на стеблинах більшості рослин. Розташовані гвинтом листя як би розкидаються на всі сторони  і не закривають один одного від світла, що вкрай необхідно для життя рослин. Це біологічне явище називається філотаксис (будова листа).  Іншою проявою філотаксиса є устрій суцвіття соняшника або луски ялинової шишки, у якої луска розташовані у вигляді спіралей та гвинтових ліній. Особливо читко це можна побачити у ананаса, який має більш менш шестикутні комірки, що утворюють ряди у різних напрямах.

 

 

 

 

 

 

 

На прикладі будь-якого дерева можна розглянути симетрії конуса. Дерево за допомогою кореневої системи має можливість поглинати вологу та поживні речовини з грунту, тобто знизу, а інші важливі функції виконуються кроною, тобто зверху. Тому напрямки «верх» та «низ» для дерева суттєво відрізняються.

На відміну від світа рослин поворотна симетрія в тваринному світі зустрічається не часто (наприклад, морська зірка та панцир морського їжака). Для комах, риб, птахів, тварин дуже важлива різниця між напрямами «вперед» та «назад». Для усіх  представників тваринного світу характерна білатеральна (дзеркальна) симетрія. Ця симетрія є у метеликів, симетрія лівого та правого проявляється у них майже з математичною строгістю.

Протягом тисяч років люди дивувалися ідеальній гексагональній формі сот і запитували себе, як бджоли можуть інстинктивно створити форму, яку люди можуть відтворити лише за допомогою циркуля і лінійки. Як і чому бджоли мають пристрасне бажання створювати шестикутники? Математики вважають, що це ідеальна форма, яка дозволяє їм зберігати максимально можливу кількість меду, використовуючи мінімальну кількість воску. У будь-якому випадку, все це продукт природи, і це вражає. (Відеофрагмент)

 

Запитання:

• Яку симетрію називають симетрією життя?
• Проведіть дослідження рослин,  які ростуть біля вашої оселі,  на симетричність.

                                                            

Чи завжди симетрію можна бачити? Чи не можна знайти симетрію на атомному рівні при вивченні речовини? Хіміки говорять, що всі тіла складаються з молекул, а молекули – з атомів. Більшість атомів розташовані у просторі за принципом симетрії. Ось структура двох простих молекул:

1) оксиду карбону CO₂,                   2) водяної пари H₂O

Обидві молекули  мають площину симетрії. Наявність дзеркальної симетрії пояснюється тим, що парні однакові атоми (атоми кисню в молекулі CO₂ або атоми гідрогену в молекулі H₂O) однаковим чином з’єднані  з третім атомом. Ніщо не зміниться, якщо поміняти місцями парні атоми в молекулі, такий обмін є дзеркальним відображенням.

У молекулі метану CH₄ атом карбона має зв'язок з чотирма  однаковими атомами гідрогена. Просторова модель молекули метану  є тетраедр, в вершинах якого знаходяться атоми гідрогена, а в центрі атом карбона.

 

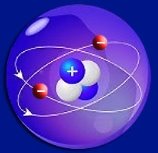
 Симетрія  атома                                                       Атом гелія

                                                                                                (He)

 

 

 

 

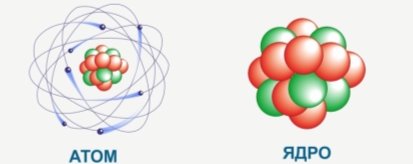
Будова молекул

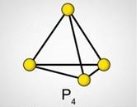
• білого фосфору:

 

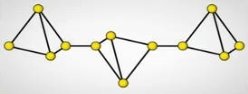
• червоного фосфору:

 

 

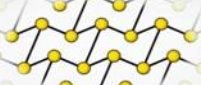
• чорного фосфору:

 

 

Виключно важливу роль у світі живої природи відіграють молекули ДНК (дезоксирибонуклеїнової кислоти).

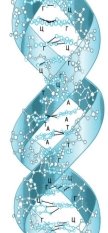Молекула ДНК складається з великого числа ланок, які називають нуклеотидами, ці ланки з’єднуються у два ланцюги. Кожен нуклеотид містить молекулу вуглеводу, залишок фосфатної кислоти( фосфат) і молекулу нітратної основи. Ланцюги нуклеотидів сполучаються між собою за допомогою водневих зв’язків. Обидва ланцюги ДНК закручені навколо спільної осі, а також один навколо одного. Основні функції ДНК – це кодування, збереження спадкової інформації та її передача дочірнім клітинам під час розмноження.

 

 

 «Вивчаючи фізику, ми з’ясовуємо, що існує велика кількість законів - закони гравітації, електрики та магнетизму, ядерної взаємодії і т.п. Але уся ця кількість законів  має деякі спільні принципи, які так чи інакше містяться у кожному законі. Прикладами таких принципів можуть слугувати деякі властивості симетрії.» Р. Фейнман

Поняття симетрії не обмежується симетрією об’єктів. Воно розповсюджується на фізичні явища та фізичні закони. Симетрія фізичних законів – це незмінність (інваріантність) по відношенню до тих чи інших перетворень, які залежать, наприклад, від умов спостереження явища.

Проблема симетрії фізичних законів цікавила вчених у зв’язку з дослідженнями, які проводилися під час створення теорії відносності. Мова йде про симетрію фізичних законів по відношенню до переходу з однієї інерційної  системи відліку в іншу інерційну систему, або симетрії фізичних законів відносно рівномірного прямолінійного руху.

Принципи симетрії поділяються на просторово-часові і внутрішні, що описують властивості елементарних частинок. Серед просторово-часових принципів симетрії можна виділити наступні:

• Зсув системи відліку не змінює фізичних законів, тобто усі точки простору рівноправні. Це означає однорідність простору.
• Поворот системи відліку просторових координат залишає фізичні закони незмінними, тобто усі властивості простору однакові по всім напрямам.
• Зсув у часі не змінює фізичних законів, тобто усі моменти часу об’єктивно рівноправні. Час однорідний. Це означає, що можна будь-який момент часу взяти за початок відліку. Цей принцип означає закон збереження енергії, що будується на симетрії відносно зсувів у часі.
• Закони природи однакові в усіх інерційних системах. У відповідності з принципом симетріє можна перейти в іншу систему відліку, яка рухається відносно даної системи з постійною за величиною і напрямом швидкістю.
• Дзеркальна симетрія природи - відображення простору у дзеркалі  - не змінює фізичних законів.
• Заміна усіх частинок на античастинки не впливає на фізичні закони, не змінює характер процесів природи.

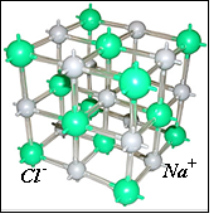Ярко і систематично симетричність структури матерії знаходиться в неживій природі, в кристалах. У своєму «Курсі кристалографії» Е.С.Федоров писав: «Кристали сяють симетрією». Перший серед дорогоцінних каменів алмаз: кристальна чистота і прозорість, чудова гра світу, ідеальна, правильна форма. З’ясовується, що кристали не тільки алмази. Звичайний цукор і поварена сіль, лід та пісок складаються з множини кристалів. Більшість будівельних матеріалів - метали, камінь, пісок, глина-кристалічні речовини. Кристали - це тверді тіла, що мають форму многогранника. Для кожної речовини існує своя ідеальна форма його кристала. Ця форма має властивості симетрії, тобто властивість суміщатися с собою у різних положеннях шляхом поворотів,  відображень,  паралельних перенесень. Внутрішній устрій кристала складається з так званою кристалічної решітки, в однакових комірках якої, що мають форму паралелепіпедів, розміщені за законами симетрії  молекули, атоми, іони або їх групи.  

Зв'язок між геометрією зовнішньої форми і внутрішньою будовою кристалів та їхніми фізичними властивостями вивчає фізична кристалографія. Шестигранні природні кристали кварцу та синтетичні кристали дігідрофосфату калію мають досить досконалу чотиригранну структуру.

 

Хто з нас взимку не був зачарований сніжинками? Кожна з них - це маленький кристал води, що замерзла. Форма сніжинок може бути різною, але всі вони є симетричними, мають поворотну симетрію, дзеркальну симетрію.

 

 

 

 

 

 

 

 

 

А що таке ферорідина?  (Відеофрагмент)

 

Ферорідина - це магнітна рідина, яка може утворювати вельми цікаві і витіюваті фігури. Втім, поки магнітне поле відсутнє, ферорідина - в'язка і ні чим не примітна. Але варто вплинути на неї за допомогою магнітного поля, як її частки вишиковуються уздовж силових ліній - і створюють щось неймовірне.

На практиці ферорідина застосовується по-різному: наприклад, для забезпечення теплопровідності в динаміках.

Можливість ставати то твердим, то рідким залежно від дії магнітного поля, робить цей матеріал значимим і для автопрому, і для NASA і для військових.

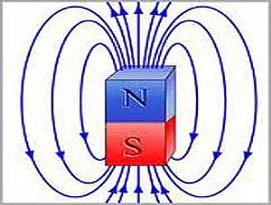Підковоподібний і штабовий магніти мають північний полюс N і південний S. Взаємодію магнітів можна пояснити тим, що магнітне поле одного магніту діє на другий магніт і, навпаки, магнітне поле другого магніту діє на перший. Лінії, уздовж яких діють магнітні сили, завжди замкнені. Поза магнітом ці лінії виходять з північного полюса і входять у південний, замикаючись у середині магніту.

Південний магнітний полюс Землі знаходиться на  півночі, але він не збігається точно з Північним географічним полюсом, а віддалений від нього приблизно на 2100 км. Північний магнітний полюс Землі міститься  поблизу Південного географічного полюса. Тому напрями на північ і південь компас показує лише наближено.

 

Ще приклади симетрії у фізиці

 

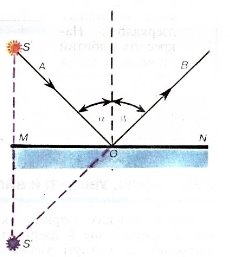
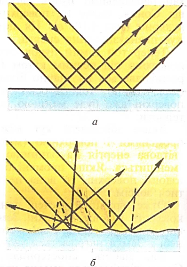
• Кут відбивання дорівнює куту падіння

 

 

 

 

 

 

 

 

 

 

 

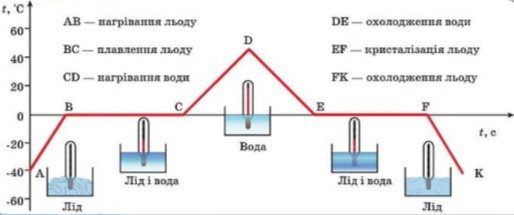
• Графік зміни агрегатного стану води

 

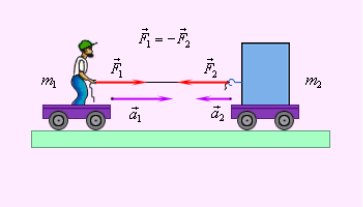
• Третій закон динаміки Ньютона: сила є наслідком взаємодії двох або більшої кількості тіл.

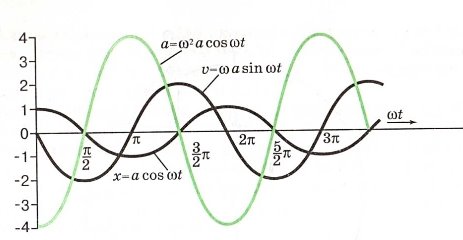• Гармонічні коливання.

 

 

 

 

 

 

 

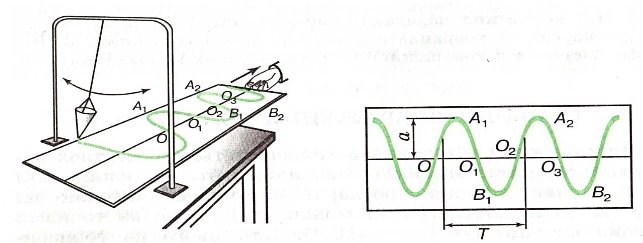
Завдання:

1. Наведіть свої приклади симетрії у фізиці.

2. Як розповсюджуються електромагнітні хвилі в взаємно перпендикулярних площинах?

 

 

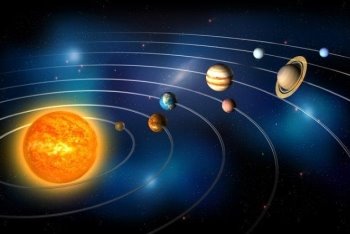Німецький фізик та астроном І. Тіціус (1729-1796) за допомогою послідовності Фібоначчі знайшов закономірність і порядок у відстанях між планетами Сонячної системи.

 

 

 

 

 

 

 

Наша Галактика Молочний Шлях - це відносно яскрава сріблясто-біла смуга на зоряному небі, яку давні греки називали «галактикос» ( від грецької «гала»-молоко). Вона має дуже добре виражену спіральну структуру, в якій дві спіралі.

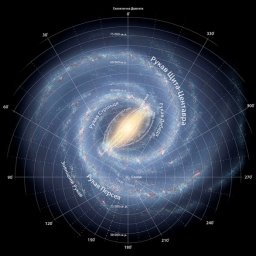Спіральна структура в наший Галактиці дуже добре розвинена. Уздовж рукавів в основному зосереджені наймолодші зірки, багато розсіяних зоряних скупчень і асоціації, а також ланцюжки щільних хмар міжзоряного газу, в яких продовжують утворюватися зірки. У спіральних гілках велика кількість змінних і спалахуючих зірок, у них найчастіше спостерігаються вибухи деяких типів наднових. На відміну від гало, де будь-які прояви зоряної активності надзвичайно рідкісні, в гілках продовжується бурхливе життя, пов'язане з безперервним переходом речовини з міжзоряного простору в зірки і назад. Галактичне магнітне поле, яке пронизує весь газовий диск, також зосереджене головним чином у рукавах.

Кожен спіральний рукав описує логарифмічну спіраль із нахилом приблизно 12°. Вважається, що у нашій галактиці існують чотири основні спіральні рукави, котрі беруть свій початок у галактичному центрі.

 

Галактика Андромеди.

Перші фотографії галактики було отримано валлійським астрономом Ісааком Робертсом 1887 року. Використовуючи власну невелику обсерваторію в Сассексі, він сфотографував і вперше відзначив спіральну структуру Галактики Андромеди^.

Симетрія Сонця-Місяця.

Сонце має діаметр 1,4 млн.км, Місяць - 3474км. Здається майже неможливим, що Місяць може блокувати сонячне світло і забезпечувати нам близько п’яти сонячних затемнень кожні два роки. Як це виходить? Так співпало,що поряд з тим, що ширина Сонця приблизно в 400 разів більше, ніж Місяць, Сонце також в 400 разів далі. Симетрія забезпечує те, що якщо дивитися з Землі, то Сонце і Місяць здаються одного розміру, і тому Місяць може закрити Сонце. Звичайно, відстань від Землі до Сонця може збільшуватися, тому іноді ми бачимо кільцеві й неповні затемнення. Астрономи не знають, як часто зустрічається така симетрія серед інших планет, але вони думають, що це досить рідкісне явище.

Сферичне Сонце обертається навколо свого центра, але це ніяк не впливає на рух Землі по орбіті. Гравітаційне поле Сонця симетричне і тому не змінюється при простому обертанні. Цій геометричній симетрії, яку відкрито ще в 17 столітті Кеплером, відповідає фізичний результат: момент імпульсу планети, що рухається по орбіті, завжди постійний. Це також відноситься до імпульсу і енергії.

 

 

Чому творчість людини має тенденцію до симетрії? Чи не тому, що «Людині потрібен порядок: без нього усі його дії втрачають логічний взаємозв’язок. Чим досконаліше порядок, тім спокійніше і впевненіше відчуває себе людина. Вона створює будови, в основі яких є порядок, який диктує їй потреба психіки, - це творчій процес. Творчість є акт впорядкованості» (архітектор Ле Корбюзьє). Інколи архітектор обмежуються симетрією прямокутного паралелепіпеда, інколи використовує більш витончену симетрію. Мистецтво архітектора починається тоді, коли вдається відшукати гармонічне та оригінальне співвідношення між симетрією та асиметрією. Більшість будівель дзеркально симетричні. Це обумовлено їх функціональною природою. Загальні плани будівель, архітектура фасадів, оформлення внутрішніх приміщень, орнаменти, карнизи, колони, стелі, якщо їх розглядати з точки зору присутніх в них просторових закономірностей, можна описати тією чи іншою групою симетрії матеріальних фігур.

 

 

 

 

 

 

 

 

 

 

 

 

В музиці та поезії  ми теж маємо справу з симетрією та асиметрією. В віршах мається на увазі симетрія чергування рим, наголосних складів, тобто ритмічність. У музиці збереження теми і її зміни (розробка, розвинення) є єдністю симетріє та асиметрії.

Приємне звучання в музиці нерідко обумовлюється симетричністю мелодії. У музиці є багато моментів, пов'язаних із симетрією, у першу чергу — це нотна нотація.:

• сам нотний стан є симетричним;
• має місце симетрія мажорного та мінорного ладів;
• зустрічаються фрагменти музичних творів із розташуванням нот на нотному стані за певними видами симетрії.

Одним з перших поняття симетрії у музиці запровадив російський і радянський музичний діяч Е. К. Розенов. В кінці XIX століття, аналізуючи твори Й. С. Баха він зробив висновок, що в них «панують закон золотого перетину і закон симетрії». (відеофрагмент)

 

Про яку симетрію можна говорити, коли дивишся на картину геніального Леонардо да  Вінчі «Мадонна Літта»? Фігури мадонни та дитини вписані в правильний трикутник, завдяки чому особливо ясно сприймаються оком глядача, мати та дитина відразу виходять на перед, стають центром нашої уваги. Голова мадонни знаходиться між двома симетричними вікнами на задньому плані. У вікнах ми бачимо спокійні горизонтальні лінії пагорбів та хмар. Усе це створює відчуття спокою, яке підсилюється за рахунок гармонічного поєднання кольорів (блакитного та жовтувато-червоного).

Внутрішня симетрія картини відчувається дуже сильно. А чи є там асиметрія?

Мадонна ніжно тримає дитину, дивиться на неї, усі її думки тільки про неї, а ось малятко дивиться на нас, таким чином внутрішня рівновага композиції порушується, замкненість картини розкривається у зовнішній світ. Якщо спробувати прибрати цю асиметрію, повернути обличчя дитини до матері, з’єднати їх погляди, чи не стане картина менш виразною?

Кожного разу, як ми захоплюємося твором мистецтва, говоримо про гармонію, красу, ми дотикаємося до проблеми співвідношення симетрії та асиметрії.

 «Математик, так само як художник або поет,

створює узори» Г. Харді.

Роспис на стіні, що прикрашає будівлі, галереї, чавунне литво, що використовують в огорожах парків, решітки мостів, кераміка – це різні види бордюрів. Бордюром називають рисунок, який періодично повторюється на довгій стрічці. Існують різні типи симетрії бордюрів: переносна симетрія, дзеркальна симетрія, поворотна симетрія, симетрія, яка має поперечні вісі симетрії, комбінована.

У декоративній художній творчості часто зустрічаються орнаменти, які містять чудове поєднання переносної, дзеркальної і поворотної симетрій.

Голандський художник Ешер створив відомі орнаменти «Летящие птицы» та «Ящерицы», перший з яких базується на похилій  решітці, другий – на гексагональній, а характерний єгипетський орнамент - на квадратній.

 

 

 

 

 

 

 

 

 

  

Запитання:

 

1. Наведіть приклади симетрії та асиметрії у відомих вам творах  мистецтва.

2. Що таке орнамент? Як створити неповторний орнамент?

 

 

Завдання:

1. Почни з простої фігури, з якої можна одержати паркет. Відріж від неї шматочок і додай до іншої сторони. Повтори цю операцію декілька разів. І фігура перетвориться на чудовий паркет.

 

2. Створи орнаменти використовуючи запропоновані елементи (геометричні фігури).

 

 

Підведення підсумків кейс-уроку

№	Назва	Зміст
1	Результати уроку можна доповнити такими знахідками
2	Які три сайти допомогли знайти важливу інформацію	https://uk.wikipedia.org/ https://www.youtube.com/ http://edufuture.biz/
3	На допомогу учню і коучу	http://edufuture.biz/ https://uk.wikipedia.org/ https://www.youtube.com/ http://simetriya.webnode.com.ua/
4	Де знаходити інформацію для кейсу	https://uk.wikipedia.org/wiki/%D0%A1%D0%B8%D0%BC%D0%B5%D1%82%D1%80%D1%96%D1%8F   https://uk.wikipedia.org/wiki/%D0%A1%D0%B8%D0%BC%D0%B5%D1%82%D1%80%D1%96%D1%8F_%D0%B2_%D0%BC%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D1%86%D1%96   https://uk.wikipedia.org/wiki/%D0%A1%D0%B8%D0%BC%D0%B5%D1%82%D1%80%D1%96%D1%8F_(%D0%B1%D1%96%D0%BE%D0%BB%D0%BE%D0%B3%D1%96%D1%8F)   https://www.youtube.com/watch?v=U1qslJ9DK1A   https://www.youtube.com/watch?v=eG0yLHos0Go
5	Локація проведення кейс - уроку	Кейс- урок проходить у класі, бібліотеці
6	Змагання	Команди хлопчиків і дівчат. Завдання: Знайдіть усі осі симетрії  куба та паралелепіпеда. Створіть орнамент із запропонованих елементів (правильний трикутник, ромб, шестикутник).
7	Домашнє завдання	Виріжте декілька фігур, які мають: 1) одну, 2) дві, 3) три, 4) чотири осі симетрії.   Сконструюйте моделі геометричних тіл, які складаються з правильних многогранників, за допомогою комп’ютерних програмних засобів.
8	Тривалість	90 хвилин (спарений урок)
9	Можливість схеми заняття з учнем-дублером	Можливо
10	Отримані знання і напрацьовані компетенції	  Уміння швидко знайти необхідну інформацію і креативно користуватися нею в практичних цілях.   Знання про симетрію в області математики, фізики, хімії, астрономії, біології, мистецтва.   Уміння конструювати «нові знання» на основі отриманих знань та їх сегментів.
11	Теги	Симетрія, центральна, осьова, дзеркальна, білатеральна симетрія тварин, фізична симетрія,кристалографія, атом, молекула, закони збереження, асиметрія, магніт, ферорідина, молекула ДНК, елементарні частинки, античастинки, галактика
12	Автори	Постнікова Тетяна Володимирівна, вчитель математики Марганецької спеціалізованої природничо-математичної школи І-ІІІ ступенів № 11 вищої кваліфікаційної категорії, «Вчитель-методист»
13	Брали участь у апгрейді кейсу	Учні 8-х, 10-х класів Марганецької ПМШ №11