УРОК ____

Тема. Розв'язування задач. Самостійна робота.

Мета уроку. Формувати вміння і навички знахо­дити елементи однієї фігури комбінації через елемен­ти іншої. Формувати наполегливість у досягненні мети, розвивати логічне мислення. Показати прак­тичне застосування здобутих знань.

ХІД УРОКУ

І. Перевірка домашнього завдання.

Запитання до задачі 1

1. Який циліндр називається рівностороннім?

(Осьовим перерізом якого є квадрат.)

2. Що спільного між описаною навколо циліндра і вписаною в нього правильними чотирикутними при­змами і чим вони відрізняються?

(Спільне: призми прямі з рівними висотами, в осно­вах лежать квадрати; відмінності: у описаної призми сторона основи 2R, а у вписаної R, де R – радіус кола основи циліндра.)

3. Чим слід замінити відношення площ бічних поверхонь призм?

(Відношенням сторін основ призм, тобто 2R:R= 2:=.)

Розв'язання задачі 2 вчитель перевіряє під час пе­ревірки зошитів.

II. Розв'язування задач.

Задачі 1 – 2 розв'язуються усно, за готовими ма­люнками.

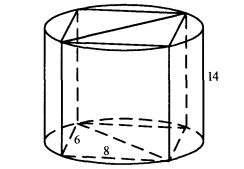
1. Прямокутний паралелепіпед, сторони основ якого 6 дм і 8 дм, вписано в циліндр з висотою 14 дм. Знайти радіус основи циліндра, площу його осьового перерізу і бічної поверхні, об'єм циліндра.

Відповідь. 5 дм, 140 дм², 140π дм², 350π дм³.

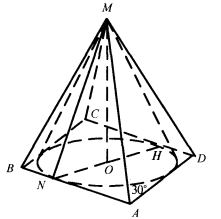2. Навколо конуса, висота якого дорівнює 10см, описано піраміду, основою якої є ромб з висотою 20 см і гострим кутом 30°.

Знайти: а) кут між твірною конуса і площиною його ос­нови;

б) площу бічної поверхні піраміди.

Відповідь. Оскільки піраміду описано навколо ко­нуса, то всі її бічні грані мають рівні висоти і нахи­лені до основи під однаковими кутами. Проведемо ΜΝ (твірну конуса, або висоту бічної грані пірамі­ди): ΜΝ А В , ON — її проекція, отже, ON АВ (за теоремою про три перпендикуляри). ON — радіус кола, вписаного в ромб, дорівнює половині висоти ромба, ON = 10 см.

< ΜΝΟ — кут між твірною і основою, tg MNO =, <MNO = 60°, <ΝΜΟ = 30°, ΜΝ = 20 см, AD = 2 · 2r = 40 (см). Площа бічної поверхні піраміди =2 · АВ · MN = 2 · 40 · 20 = 1600 (см²).

Відповідь, а) 60°; б) 1600 см².

III. Самостійна робота.

Робота проводиться в групах, які сформовані так, що в кожній є 1—2 сильніших учні-консультанти. Під час виконання самостійної роботи вчитель надає необхідні консультації. Перевіряючи зошити, звертає увагу на правильність виконання малюнків. В оцінці враховуються відповіді учнів на запитання вчителя.

1. Навколо циліндра, висота якого 15 см, а радіус основи 5 см, описано пряму призму. Основою при­зми є ромб зі стороною 12 см. Знайти площу осьово­го перерізу циліндра, об'єми призми і циліндра.

Розв'язання

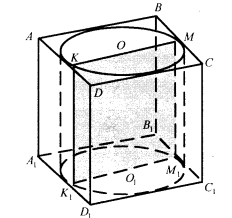Прочитавши умову, учні аналізують зображення ромба, описаного навколо кола (задача 2 усних вправ). Роблять висновок, що діаметр NH не може бути па­ралельним сторонам AD, BC ромба (мал. до задачі 2, с. 17). Суттєвим є вибір точки N на стороні ромба, яку приймаємо за точку дотику. Вона не може бути серединою відрізка АВ, якщо ромб не є квадратом.

Призму описано навколо циліндра, тому площи­ни їх основ збігаються, довжина твірної циліндра дорівнює його висоті і довжині бічного ребра при­зми. Отже, АА₁ = 15 см.

Висотою ромба, що лежить в основі призми, є К₁М₁ — діаметр кола основи циліндра.

Осьовий переріз циліндра K₁KMM₁ — прямокут­ник, КМ=10см, MM₁=15см. Площа осьового перерізу S = KM · MM₁ = 10 · 15 = 150 (см²). Об'єм призми обчислюємо за формулою V = S_oH.

 S_o = AD · KM = 12 · 10 = 120 (см²), V_п = 120 · 15 = 1800 (см³).

Об'єм циліндра обчислюємо за формулою V_ц = πr²H , де г = O₁K₁,

V_ц = π·25·15 = 375π (см³).

Відповідь. 150см², 1800см³, 375 π см³.

2. У конус вписано правильну трикутну піраміду. Сторона її основи дорівнює а, кут між площинами основи і бічної грані α . Знайти радіус основи, висо­ту, твірну, площу осьового перерізу і площу бічної поверхні конуса.

Розв'язання

Учитель звертає увагу учнів на те, що осьовий пе­реріз даного конуса — трикутник, сторонами якого є бічне ребро піраміди, діаметр основи конуса, що проходить через основу цього бічного ребра, і твірна конуса, що проходить через інший кінець цього діа­метра, а не висота або апофема піраміди.

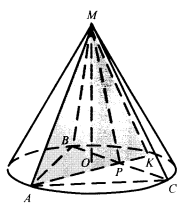Піраміду вписано в конус, тому площини їх ос­нов і вершини збігаються, МО — висота конуса і піра­міди. АР BC , МР BC (за теоремою про три пер­пендикуляри), ВР = PC, кут між бічною гранню ВМС

і основою АВС – < МРО = α.

АО=R=.

Проведемо діаметр АК і сполучимо точку Μ з точ­кою Κ. Δ АМК — осьовий переріз конуса, AM = МК, його площа

S = АК · МО = АО · МО = RH .

У  ΔРМО (<МОР = 90°) ОР = R =,  МО = ОР tgOPM = tgα.

Площа осьового перерізу конуса .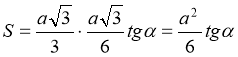

Твірна конуса l = AM = (з ΜΑΟ, <ΑΟΜ =90°).

.

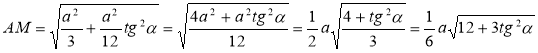Площа бічної поверхні конуса .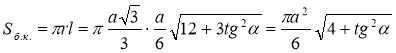

Відповідь. R=; Н== tgα; ;;

.

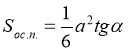3. Для будівництва школи потрібно привезти 18 плит перекриття, виготовлених із залізобетону, гус­тина якого 2200 кг/м³. Плита має вигляд прямокут­ного паралелепіпеда шириною 1,3 м, довжиною 4,9 м і висотою 0,2 м. У цій плиті проходять наскрізні (на всю довжину) 6 отворів, діаметр кожного з яких до­рівнює 0,16 м. Скільки ходок 10-тонного автомобіля слід замовити для перевезення плит?

Зауваження. Всі обчислення виконувати за прави­лами дій з наближеними числами, відповідь записати натуральним числом.

Розв'язання

Маса плити обчислюється за формулою т = ρ V . Об'єм прямокутного паралелепіпеда V= 1,3 · 4,9 · 0,2 1,27 (м³).

Об'єм циліндричного отвору  V_ц = πr²Н = 3,14 · 0,08² · 4,9 0,10 (м³).

Об'єм плити дорівнює V - 6V_ц . V_плити = 1,27 – 6 · 0,10 = 0,67(м³).

Маса плити т = 2200 · 0,67 = 1474 (кг) 1,5 т; 10-тонний автомобіль може перевезти 10 : 1,5 я 6 плит. Для перевезення 18 плит потрібно замовити 3 ходки.

Відповідь. З ходки.

IV. Домашнє завдання.

Повторити п. 34 (Площа ортогональної проекції многокутника). Розв'язати задачі:

1. У правильній чотирикутній піраміді сторона основи дорівнює а, плоский кут при вершині — α . Визначити об'єм конуса, вписаного в піраміду.

2. У правильній трикутній призмі через сторону нижньої основи і протилежну вершину верхньої про­ведено переріз площею S, який утворює з площиною основи кут α . Знайти бічну поверхню циліндра, опи­саного навколо даної призми.