Анотація

У роботі описана у загальному вигляді методика розв’язування задач за темою «Комплексне застосування законів Ньютона при розв’язуванні задач з розділу «Динаміка», зроблено особливий акцент на важливості використання всіх трьох законів Ньютона у своїй сукупності і взаємозв’язку незалежно від конкретного виду задачі. На конкретних прикладах показано важливість глибокого аналізу фізичної картини взаємодії тіл для правильного розв’язку задач. Проаналізовано використання терміну “доцентрова сила” у курсі елементарної фізики. Показано, що і для прояснення фізичної суті задачі, і для самого розв’язування введення поняття “доцентрова сила” є фізично необґрунтованим і зайвим.

 

Зміст

 

Вступ                                                                                                                            2

Теоретична частина                                                                                                      3

Практична частина                                                                                                       6

Перелік посилань                                                                                                        18

 

 

Вступ

 Вивчення фізики є невід’ємною частиною повноцінної освіти, яка полягає не тільки у одержанні певної суми знань у деякій галузі, але й у всебічному розвитку особистості людини. Значення фізики у формуванні наукового світогляду визначає її роль незаперечного лідера сучасного природознавства. Фізика задає стиль наукового мислення, який вирізняється високим ступенем досконалості і збалансованості якісного і кількісного опису явищ природи. Добре відомо, що розв’язування задач є одним з найефективніших засобів засвоєння фізики, надійним інструментом для контролю рівня розуміння фізичних законів. Робити висновки про ступінь розуміння фізичних законів можна за умінням свідомо застосовувати їх для аналізу конкретних фізичних явищ, зокрема, для розв’язування задач. Досвід викладання показує, що можливо найбільшу складність для учнів становить питання “з чого почати? ”, тобто не безпосереднє застосування фізичних законів, а саме вибір, які власне закони і чому слід застосувати для аналізу конкретного фізичного явища. Ось це уміння вибрати правильний шлях розв’язування задачі якраз і свідчить про глибоке і всебічне розуміння фізики. Саме тому у теоретичній частині даної роботи зроблено спробу описати у загальному вигляді методику того, з чого слід починати розв’язування задачі. У практичній частині даної роботи розглянуті декілька прикладів, які підібрані таким чином, щоб допомогти учням розібратись у розв’язуванні деяких задач, які часто викликають труднощі і певне нерозуміння.

 

 

Теоретична частина

 

Мета роботи: вивчення законів Ньютона у процесі розв’язування задач за темою «Комплексне застосування законів Ньютона при розв’язуванні задач з розділу «Динаміка» та розвиток уміння застосовувати їх на практиці, з’ясування важливості глибокого аналізу фізичної картини взаємодії тіл для правильного розв’язку задач.

У другому розділі механіки, а саме «динаміці», у курсі елементарної фізики, який вивчають у школах, коледжах, ліцеях, технікумах, професійно-технічних училищах, розглядаючи рух фізичних тіл, практично завжди використовують фізичну модель «матеріальна точка». Саме тому ми будемо говорити про динаміку матеріальної точки, нехтуючи геометричними розмірами тіла і розглядаючи його рух як рух точки – центра мас.

 Основою динаміки є три закони Ньютона. Починаючи розв’язування задач на цю тему, слід одразу ж наголосити на важливості використання всіх трьох законів у своїй сукупності і взаємозв’язку незалежно від конкретного виду задачі. Пояснимо це.

1.                 Цілком очевидно, що будь-який опис механічного руху має зміст лише при зазначенні системи відліку, відносно якої виконані вимірювання положення, швидкості і прискорення тіла, рух якого нас цікавить, а також сил, що діють на дане тіло. І оскільки у курсі елементарної фізики вивчають тільки інерціальні системи відліку (власне, саме ті, про які йде мова у першому законі Ньютона), розв’язування задачі слід починати з вибору певної інерціальної системи відліку. У разі нетривалого руху тіла (у порівнянні, наприклад, з тривалістю доби) за таку інерціальну систему відліку можна прийняти землю або будь-яке тіло, що рухається відносно неї рівномірно і прямолінійно. Отже, посилання на перший закон цілком закономірне. 

2.                 Визначити характер руху тіла неможливо без аналізу сил, що діють на нього. Але ми добре пам’ятаємо, що сила – це міра взаємодії тіл. Це означає, що без розгляду взаємодії тіла, рух якого нас цікавить, з іншими тілами, задачу розв’язати не можна. А проаналізувати взаємодію, а отже, і визначити всі сили, які діють на досліджуване нами тіло, неможливо без застосування третього закону Ньютона.

3.                 І нарешті, оскільки зміна швидкості тіла визначається його прискоренням, а прискорення визначають із другого закону Ньютона, то очевидна і зрозуміла необхідність використання цього закону у процесі розв’язування задач. Необхідно, щоб учні чітко зрозуміли взаємозв’язок всіх трьох законів Ньютона і використовували це, розв’язуючи задачі. 

Задачі на динаміку матеріальної точки зручно розв’язувати у такій послідовності:

1.                 Чітко уявивши за умовою задачі фізичний процес, слід зробити рисунок (схематичне креслення, ескіз) і зобразити на ньому всі тіла, які беруть участь у русі розглядуваного тіла, а також всі елементи зв’язків між ними (нитки, канати, пружини тощо). 

2.                 Показати на рисунку у вигляді векторів всі сили, прикладені до тіл, рух яких будуть вивчати. Слід пам’ятати, що сили можуть діяти на дане тіло тільки з боку якихось інших тіл. А саме: з боку землі – це сила тяжіння mg (у цих методичних рекомендаціях вектори ми будемо позначати виділеним шрифтом), з боку мотузки, канату, нитки тощо – це сила натягу F_н, з боку різних пружин – це сила пружності F_пр, з боку опор, підставок – це сила реакції опори (або просто реакція опори) N, і, якщо поверхні взаємодіючих тіл шорсткі – це сила тертя F_тер. У деяких задачах слід враховувати силу опору F_оп, яку створює середовище (повітря, вода). Зображуючи вектори сил, слід пам’ятати, що:

1)                сила тяжіння mg напрямлена вертикально вниз (у разі якихось складніших рисунків – до центра Землі); 

2)                сила натягу F_н мотузки (канату, нитки) напрямлена уздовж мотузки (канату, нитки) від тіла;

3)                сила пружності F_пр напрямлена уздовж пружини від тіла, якщо у процесі руху пружина розтягнута, і до тіла, якщо пружина стиснута;

4)                сила реакції опори N, напрямлена перпендикулярно до поверхні дотику тіла з опорою (підставкою, землею тощо);

5)                сила тертя ковзання F_тер напрямлена уздовж дотичної до поверхні взаємодіючих тіл у бік, протилежний швидкості руху тіла;

6)                сила опору середовища F_оп напрямлена у бік, протилежний вектору швидкості тіла.

Оскільки мова йде про динаміку матеріальної точки, то зручно прикладати всі сили, які діють на розглядуване тіло до певної точки цього тіла, а саме – до центра мас. Строго кажучи, такий вибір точки прикладання сил не є обов’язковим, але, на нашу думку, є найбільш логічним і природним.  

3.                 Показати напрями прискорень тіл, якщо це можна зробити апріорі, на підставі тільки умови задачі, або вибрати ці напрями довільно на підставі досвіду і фізичної реальності такого вибору.

4.                 Вибрати інерціальну систему відліку, відносно якої будуть розглядати рух тіла (чи декількох тіл, якщо цього вимагає умова задачі). Напрям осей системи координат слід вибирати у найбільш зручний для розв’язування задачі спосіб. У деяких задачах, де необхідно аналізувати рух декількох тіл, зручно вибрати свій напрям осей координат для кожного із цих тіл. При цьому, для зручності, напрям однієї з осей координат вибирають за напрямом вектора прискорення тіла.

5.                 Записати рівняння другого закону Ньютона для кожного з тіл, рух яких розглядають, у векторній формі.

6.                 Записати рівняння другого закону Ньютона у проекціях векторів сил і прискорень на осі вибраної системи координат. Зазначимо, що на практиці у ході розв’язування задачі дуже часто одразу ж записують рівняння другого закону Ньютона у проекціях векторів на осі координат. На наш погляд, такий підхід виправданий, якщо добре розуміють фізичну суть задачі. 

Розглянемо декілька прикладів у загальному вигляді. Приклади підібрані таким чином, щоб допомогти розібратись у розв’язуванні деяких задач, які часто викликають труднощі і певне нерозуміння.

  

Практична частина

Задача 1. Підкинутий камінь масою m летить вгору з початковою швидкістю v₀. Визначити висоту, на яку підніметься камінь, якщо середня сила опору повітря становить F_оп.

1.                 Ця, здавалось би тривіальна задача, інколи викликає труднощі вже на етапі визначення сил, які діють на камінь. Окремі учні, зважаючи на те, що камінь летить вгору, починають шукати деяку рушійну силу, яка і спричиняє такий рух. Тому на самому початку слід наголосити на важливості визначення тіл, взаємодія з якими для руху каменя є суттєвою. У даному разі це земля (її дію на камінь позначаємо силою mg) і повітря (сила F_оп). Позначаємо ці сили на рисунку до задачі (рис.1).

Позначаємо також і напрям прискорення, з яким рухається камінь. 

2.                 Природно за систему відліку вибрати землю і зв’язати з нею систему координат. У даному разі достатньо однієї осі координат (зазвичай у задачах такого типу використовують позначення – вісь oy), початок відліку зв’язуємо з поверхнею землі (рис.1). А далі будуємо логічний ланцюжок розв’язку задачі. З кінематики відомо, що шукана висота

v02

                                                                                                       H        ,                                        (1)

2 a

Отже, необхідно визначити прискорення руху каменя. За другим законом Ньютона у проекціях векторів сил і прискорення на вісь oy одержимо:

mg  F^оп

                                                                                                 a                ,

m

або

mg  F^оп

a       .                                 (2) m

Підставляємо (2) в (1) і одержуємо кінцеву формулу для визначення шуканої висоти:

mv02

                                                                                                       H                       .                           (3)

2(mg  F_оп)

Слід зупинитися ще на одному терміну, використаному у цьому прикладі:

середня сила опору повітря. Інколи учні ставлять питання: як розуміти цей термін?

Отже, необхідно нагадати, що реальна сила опору повітря рухомому тілу не є сталою величиною, а залежить від швидкості руху тіла. Для помірних швидкостей (приблизно до 30 м/с) сила опору пропорційна швидкості руху тіла. Оскільки програмою курсу елементарної фізики не передбачений розгляд руху тіла в умовах дії на нього сил, які постійно змінюються (за винятком лінійно залежної від величини деформації сили пружності), то вплив опору повітря пропонують розглядати як дію деякої усередненої сили опору, яка не змінюється з часом. 

Досить часто у збірниках пропонують задачі на формальне застосування законів Ньютона без з’ясування реальних фізичних механізмів взаємодії тіла, рух якого нас цікавить, з іншими тілами. Розглянемо, наприклад, таку задачу (див. подібні задачі: №№273, 274, 275 [1], №34 [2]).

Задача 2. Сила тяги автомобіля масою m становить F_тяг. Знайти прискорення, з яким рухається автомобіль по горизонтальній дорозі, якщо коефіцієнт тертя дорівнює μ.

 

 

 

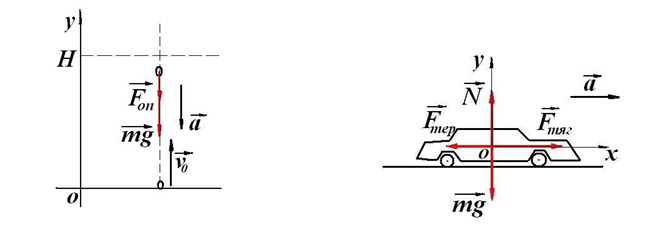
                                               Рис.1.                                                        Рис.2.

 

Автори таких задач розглядають рух автомобіля за умови дії на нього таких сил: сили тяжіння mg, сили реакції опори N, сили тяги F_тяг і сили гальмівного тертя F_тер (рис.2). При цьому модуль сили тертя визначають за формулою сили тертя ковзання F_тер = μ∙N. Зрозуміло, що розв’язок задачі у цьому разі є тривіальним. 

1.   Позначаємо на рисунку до задачі вектори сил, що діють на автомобіль, і вектор прискорення.

2.   За інерціальну систему відліку вибираємо землю і зв’язуємо з нею систему координат (рис.2). Вісь ox зручно направити за напрямом прискорення. Зазвичай систему координат зображують саме так як показано на рис.2, розташовуючи початок відліку у центрі мас рухомого тіла. Тому, інколи учні роблять висновок, що система відліку зв’язана з автомобілем. Слід одразу ж роз’яснити, що це, безперечно, не так і такий спосіб представлення системи відліку на рисунку вибирають з огляду на зручність знаходження проекцій сил у ході подальшого розв’язування задачі.

3.   Записуємо у векторній формі другий закон Ньютона

                                                                         F_тяг + mg + N + F_тер = ma.                                   (4)

4.   Проектуємо вектори на осі ox і oy. Одержимо:

                                                                        F_тяг – F_тер = ma,                                                  (5)

                                                                      N – mg = 0.                                                         (6)

З формул (5) і (6) визначаємо шукане прискорення:

                                                                      a  Fтяг  mg .                                              (7)

m

Очевидно, однак, що у цьому разі зовсім не розглядають реальні фізичні механізми взаємодії автомобіля з оточуючими тілами. Тому, коли трапляються задачі, де потрібен аналіз таких механізмів, учні відчувають значні труднощі. Проаналізуємо, наприклад, таку задачу.

 

Задача 3.  Знайти максимальне прискорення з яким може рухатись автомобіль масою m вгору по похилій дорозі з кутом нахилу α, якщо коефіцієнт тертя шин автомобіля об дорожнє покриття становить μ, а середня сила опору повітря

дорівнює F_оп.  

1.                 У цьому разі одразу ж виникає питання стосовно рушійної сили, тобто сили, яка змушує автомобіль рухатись. Деякі учні схильні вважати, що такою рушійною силою у випадку автомобілів, тракторів, мотоциклів є сила тяги двигуна. Однак, строго кажучи, це неправильно. Якщо перелічені механізми обладнані, наприклад, двигунами внутрішнього згоряння (а можливі гіпотетичні випадки реактивних двигунів ми тут не розглядаємо), то таке тіло не може надати саме собі прискорення. Це можливо лише за умови взаємодії його з іншими тілами. Отже, яке ж походження цієї самої сили тяги, що надає автомобілю прискорення? Коли працює двигун відповідні механізми передають зусилля, яке створюється у циліндрах двигуна, на колеса. Колеса, взаємодіючи з землею, відштовхують її з силою F_т1 (рис.3). Але, за третім законом Ньютона, земля також штовхає колеса, а отже і автомобіль, з силою F_т2 , рівною за модулем і протилежною за напрямом силі F_т1. Це і є фізична природа сили тяги. Фактично сила тяги – це реакція дії коліс на землю. Якщо виключити взаємодію коліс із землею (наприклад, поставити автомобіль на поверхню, вкриту гладенькою кригою), двигун не зможе надати автомобілю прискорення. Отже, можна стверджувати, що у даному разі автомобіль приводить в рух сила тертя спокою, яку у таких випадках часто називають силою рушійного тертя на відміну від сили гальмівного тертя. Як відомо сила тертя спокою може змінюватись від 0 до свого максимального значення, рівного F_т.мaк = μ∙N, де N – сила реакції опори, яка за модулем дорівнює силі нормального тиску, з якою притиснуті тіла одне до одного. Зрозуміло, що сила рушійного тертя напрямлена у бік руху тіла. У загальному випадку цю силу можна визначити тільки з другого закону Ньютона. Однак, у даній задачі вимога максимальності прискорення руху автомобіля диктує необхідність максимально можливого значення сили тертя спокою. Отже, за

модулем F_т2 = F_т.мaк = μ∙N. 

2.                 Інерціальну систему відліку зв’язуємо, як і у попередніх задачах, з землею. При цьому систему координат орієнтуємо так, як показано на рис.3. Слід пояснити учням, що така орієнтація системи координат максимально спрощує розв’язок задачі. У процесі розв’язування задачі це необхідно показати.

3.                 За другим законом Ньютона у проекціях векторів сил і прискорення на осі ox і oy у вибраній системі відліку (рис.3), одержимо:  

F_т2 – F_оп – mg·sinα = ma,    (8) N – mg·cosα = 0.      (9) З рівняння (9) визначаємо реакцію опори, N = mg·cosα, і підставляємо у (8):

μ∙ mg·cosα – F_оп – mg·sinα = ma.                             (10) З рівняння (10) визначаємо шукане прискорення:

mg(cos sin)  F^оп

                                                             a                                          .                           (11)

m

Простий аналіз формули (11) показує, що навіть у разі нехтування опором повітря (F_оп = 0), рух автомобіля вгору по похилій дорозі з прискоренням можливий лише за умови виконання нерівності μ·cosα > sinα, або μ > tgα. Якщо ж враховувати опір повітря, то коефіцієнт тертя повинен бути ще більшим. 

 

Інколи у задачах мова йде про різні види тертя. У цьому разі важливо на самому початку з’ясувати, яка сила тертя є рушійною, а яка гальмівною. Як приклад, розглянемо таку задачу (див. подібну задачу №248 [1]).

           

Задача 4. Яку найбільшу кількість вагонів може тягнути вгору по залізничній колії з кутом нахилу α тепловоз, якщо відомо, що маса тепловоза у три рази більша маси одного вагона. Коефіцієнт тертя спокою μ₁, а коефіцієнт тертя кочення μ₂. 

1.   У цій задачі зручно розглядати увесь потяг як єдине ціле, не виокремлюючи тепловоз і вагони. У даному разі сила тертя спокою F_т.мaк коліс тепловоза об рейки залізничної колії і є тією рушійною силою, яка зумовлює рух потяга. Сила тертя кочення F_т.коч є силою гальмівного тертя, яка заважає руху потяга. Вимога визначення найбільшої кількості вагонів, які може тягнути за цих умов тепловоз, одразу ж диктує такі висновки: по-перше, сила тертя спокою повинна бути максимальною (тому так її і позначаємо: F_т.мaк), по-друге, потяг рухається з постійною швидкістю (тобто, прискорення a=0). Для зручності позначимо масу одного вагона m. Тоді маса всіх вагонів становить n∙m (де n – шукана кількість вагонів), а маса тепловоза дорівнює 3m. Отже, сумарна маса потяга становить M = m∙(n + 3). Показуємо на рисунку до задачі всі сили, які діють на потяг: сумарна сила тяжіння Mg, сумарна сила реакції опори N, сила тертя спокою F_т.мaк, сила тертя

кочення F_т.коч (рис.4).

 

 

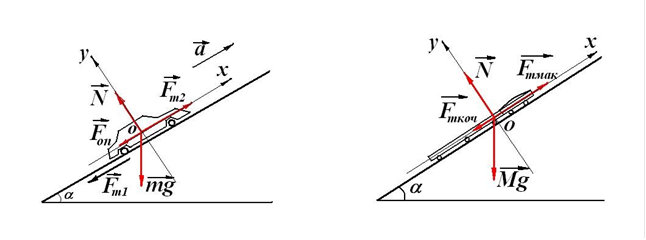
                                               Рис.3.                                                        Рис.4.

 

2.   Як і у попередніх задачах, інерціальну систему відліку зв’язуємо з землею. Систему координат орієнтуємо так, як показано на рис.4.

3.   Записуємо рівняння другого закону Ньютона у векторній формі. Оскільки рух потяга є рівномірним, то одержимо:

                                                               F_т.мax + Mg + N + F_т.коч = 0.                                (12)

4.   Проектуємо вектори на осі ox і oy:

                                                              F_т.мaк – F_т.коч – Mg·sinα = 0,                                (13)

                                                             N – Mg·cosα = 0.                                                (14)

Силу тертя кочення визначають у курсі елементарної фізики, здебільшого, так само, як і максимальну силу тертя спокою чи силу тертя ковзання з відповідною заміною коефіцієнта тертя. Отже, F_т.коч = μ₂∙N, де μ₂ – безрозмірний коефіцієнт тертя кочення. Однак, у деяких підручниках (див., наприклад, [3]) пропонують поглиблений підхід до розуміння фізичної природи сили тертя кочення. Особливої проблеми тут немає, оскільки з умови задачі повинно бути зрозуміло, у який спосіб слід визначати силу тертя кочення. З рівняння (14) визначаємо N = Mg·cosα, і одержуємо:

F_т.коч = μ₂∙ Mg·cosα,

або                                  F_т.коч = μ₂∙ m∙(n + 3)g·cosα.                             (15)

Аналогічно визначаємо максимальну силу тертя спокою F_т.мaк, яка у цій задачі є рушійною силою. Отже, F_т.мaк = μ₁∙ N₁, де N₁ – реакція опори, яка діє тільки на тепловоз. Зрозуміло, що N₁ = 3mg·cosα, і відповідно

                                                                          F_т.мaк = μ₁∙ 3mg·cosα.                                    (16)

Вирази (15) і (16) підставляємо у (13):

                   μ₁∙ 3mg·cosα – μ₂∙ m∙(n + 3)g·cosα – m∙(n + 3)g·sinα = 0,                           

або       μ₁∙ 3·cosα – μ₂∙(n + 3)·cosα – (n + 3)·sinα = 0,                       (17) З рівняння (17) визначаємо шукану кількість вагонів n:

3[(¹ ²)cos sin]

                                          n  .                                        (18)

sin₂ cos

 Розглянемо ще один тип задач, розв’язування яких інколи викликає у учнів значні труднощі. Це задачі, пов’язані з рухом тіла по криволінійній траєкторії і, як частинний випадок, по колу. У стандартних курсах елементарної фізики зазвичай обмежуються розглядом рівномірного руху по колу. При цьому вводять поняття доцентрового прискорення, яке у цьому разі є постійною величиною, рівною a_n = v²/R, де v – лінійна швидкість руху тіла по колу, R – радіус кола. І оскільки причиною появи у тіла прискорення є дія сили (у загальному випадку – декількох сил), то інколи для позначення такої сили використовують термін: доцентрова сила. Цей, на перший погляд, логічний термін спричиняє, однак, згодом досить серйозні проблеми у розумінні учнями фізичних механізмів взаємодії між тілами у тій чи іншій задачі. Тому слід докладніше зупинитися на цьому питанні. Добре відомо, що при русі тіла по криволінійній траєкторії воно має певне прискорення а, яке напрямлене за напрямом дії рівнодійної всіх сил, прикладених до тіла (рис.5). Вектор цього прискорення  а можна представити у вигляді суми двох складових: нормального або доцентрового прискорення а_n, яке напрямлене по нормалі до вектора миттєвої швидкості v, і тангенціального прискорення а_τ, яке напрямлене уздовж дотичної до траєкторії. Доцентрове прискорення а_n пов’язане зі зміною напряму швидкості, тангенціальне прискорення а_τ пов’язане зі зміною модуля швидкості. Слід одразу ж наголосити на тому, що у загальному випадку у разі зміни модуля швидкості, автоматично змінюється і доцентрове прискорення, a_n = v²/R. За другим законом Ньютона нормальна складова рівнодійної сил, яка надає тілу доцентрового прискорення, дорівнює за модулем F_n = m∙v²/R, де m – маса тіла. Ось, власне, саме цю складову і називають доцентровою силою. Саме по собі використання терміну «доцентрова сила» можливо і не становить якоїсь небезпеки, якщо у ході розв’язування задачі з’ясувати фізичну природу сили, що надає тілу доцентрового прискорення (див., наприклад, задачі №№ 30, 31 [4]). Якщо ж цього не робити, то поступово в учнів виникає уявлення про існування специфічної «доцентрової сили» як окремого виду сил у природі. Тому дуже важливо, розв’язуючи ту чи іншу задачу, одразу ж з’ясовувати фізичну природу сил, які надають тілу прискорення, зокрема, доцентрового а_n. Розглянемо, наприклад, таку задачу.

 Задача 5. Тягарець, підвішений на нитці довжиною l, рівномірно рухається в горизонтальній площині по коловій траєкторії (конічний маятник). Якою є лінійна швидкість руху тягарця, якщо під час його руху нитка утворює з вертикаллю кут α (рис.6). Опором повітря знехтувати.

1.                 Оскільки тягарець рухається по колу, то він має доцентрове прискорення а_n. Очевидно також, що шукану величину лінійної швидкості слід шукати саме із формули доцентрового прискорення, a_n = v²/R, де v – лінійна швидкість руху тягарця по колу, R – радіус кола. Аналізуючи взаємодію тягарця з оточуючими тілами, доходимо висновку, що у цьому разі суттєвою є його взаємодія із землею (сила тяжіння mg) і з ниткою (сила натягу нитки F_н). Отже, можна зробити очевидний висновок: доцентрового прискорення тягарцю надає рівнодійна сил тяжіння mg і натягу нитки F_н (рис.6). Надалі цей висновок ми ще більше конкретизуємо, проектуючи сила на відповідні осі координат. 

2.                 Інерціальну систему відліку зв’язуємо з землею. Систему координат орієнтуємо таким чином, щоб у певні моменти часу тягарець проходив через початок координат (рис.6). Така орієнтація системи координат максимально спрощує розв’язування задачі.

 

 

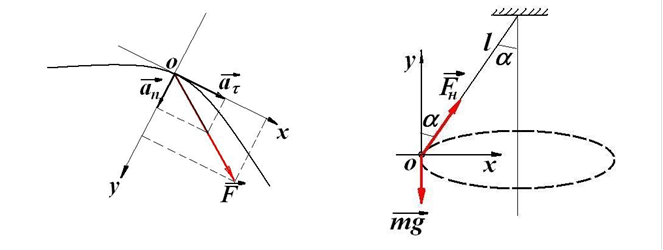
                                               Рис.5.                                                        Рис.6.

 

А тепер запишемо рівняння другого закону Ньютона у проекціях векторів на відповідні осі.

                                                                                     F_н·sinα = ma_n ,                                  (19)

                                                                                     F_н·cosα – mg = 0.                             (20)

З рівняння (19) випливає ще більш конкретний висновок: доцентрового прискорення надає тягарцю горизонтальна складова сила натягу нитки F_н. Отже, фізична картина цієї задачі стає цілком зрозумілою, і немає жодної потреби вводити у розгляд поняття «доцентрова сила». Оскільки, R = l ·sinα, то a_n = v²/(l ·sinα). Підставляючи цей вираз для a_n у рівняння (19), одержимо таку систему рівнянь:

                                                                                    F_н·sinα = mv²/(l·sinα) ,                      (21)

                                                                                     F_н·cosα = mg.                                   (22)

Поділивши рівняння (21) на (22), одержимо:

                                                                                    tgα = v²/(gl·sinα) .                             (23)

З рівняння (23) визначаємо шукану лінійну швидкість руху тягарця по коловій траєкторії:

                                                                                         v  g l tgsin.                     

 Задача 6. На краю двосторонньої похилої площини з кутом нахилу α знаходиться маленький брусок. Площину рівномірно обертають навколо вертикальної осі з кутовою швидкістю ω (рис.7). Відстань від бруска до осі обертання площини дорівнює R. Знайти мінімальне значення коефіцієнта тертя, за якого брусок ще утримується на похилій площині, що обертається.

1.                 У таких задачах зазвичай розглядають дію на брусок трьох сил: сили тяжіння mg, сили реакції опори N і сили тертя спокою F_т. Тому може виникнути логічне питання: чому взаємодію бруска з двома тілами, землею і похилою площиною, ми описуємо трьома силами? Насправді сил є дві: сили реакції опори N і сили тертя спокою F_т є, по суті, складовими так званої узагальненої реакції опори. Іншими словами, узагальнена реакція опори є рівнодійною цих двох сил. Однак, для розв’язування задач зручніше одразу ж розкладати цю узагальнену реакцію опори на такі дві складові. Брусок рухається по коловій траєкторії з постійною за модулем швидкістю. Отже, у кожній точці такої траєкторії він має незмінне за модулем доцентрове прискорення. Як і у попередній задачі висновок однозначний: доцентрового прискорення бруску надає рівнодійна сил тяжіння mg , сили реакції опори N і сили тертя спокою F_т (рис.7). Одразу ж зауважимо, що вимога знаходження мінімального значення коефіцієнта тертя диктує необхідність

розглядати максимальне значення сили тертя спокою, F_т = F_т.мaк = μ∙N. 

2.                 Інерціальну систему відліку, як і у попередніх задачах, зв’язуємо з землею. Систему координат орієнтуємо таким чином, щоб напрям осі ox збігався з напрямом вектора доцентрового прискорення у ті моменти часу, коли брусок у процесі обертання проходить через початок координат (рис.7). Наголосимо ще раз, що система відліку зв’язана не з бруском, як інколи помилково думають, а із землею. А саме такий вибір початку системи координат та її орієнтації пов’язаний виключно з бажанням максимально спростити розв’язок задачі. Запишемо рівняння другого закону Ньютона у проекціях векторів на осі ox і oy у вибраній системі відліку:

                                                                      F_т.мaк·cosα – N·sinα = ma_n ,                                 (24)

                                                                     N·cosα + F_т.мaк·sinα – mg = 0,                             (25)

де m – маса бруска. З рівняння (24) випливає, що величину доцентрового прискорення бруска визначає алгебраїчна сума проекцій сил F_т і N на вісь ox. І максимально можливе значення доцентрового прискорення, яке може бути забезпечене за певного значення коефіцієнта тертя μ, визначається максимальною силою тертя спокою F_т.мaк. Таким чином, знову немає жодної потреби вводити у розв’язок поняття «доцентрова сила», яке у цій ситуації може лише ускладнити розуміння фізичної картини. Оскільки, a_n = ω²∙R, а F_т.мaк = μ∙N, то, підставляючи ці вирази в рівняння (24) і (25), одержимо таку систему рівнянь:

                                                                         μ∙N ·cosα – N·sinα = m∙ω²∙R ,                                

                                                                         N·cosα + μ∙N ·sinα – mg = 0,                                 

або                                     N·(μ∙cosα – sinα) = m∙ω²∙R,                             (26)

                                                                            N·(cosα + μ∙sinα) = mg.                             (27)

Поділивши рівняння (26) на (27), одержимо:

cossin ² R

                                                                                                                                 .                          (28)

cossin g

Звідси і знаходимо мінімальне значення коефіцієнта тертя, за якого брусок буде утримуватись на похилій площині за такої кутової швидкості ω її обертання навколо вертикальної осі.

² Rcos gsin

 .   (29) gcos² Rsin

Одержану формулу (29) корисно проаналізувати детальніше. Зокрема, з (29) випливає, що для утримання бруска на похилій площині, насамперед, повинна бути виконана умова g∙cosα – ω²∙R∙sinα > 0, або tgα < g/(ω²∙R). Якщо, наприклад, збільшуючи кутову швидкість обертання, цю умову порушують, то ніяка сила тертя спокою вже не зможе утримати брусок на похилій площині.

 Розглянемо ще одну задачу, для розв’язування якої, щоправда, потрібно знати закон збереження повної механічної енергії.

Задача 7. Маленьке тіло масою m зі стану спокою зісковзує без тертя з вершини півкулі радіусу R (рис.8). З якою силою воно буде тиснути на поверхню півкулі, проходячи точку, яка розташована на висоті h від вершини півкулі? На якій висоті від вершини тіло відірветься від поверхні півкулі?

1.                 Тіло, рухаючись по поверхні півкулі до моменту відриву від неї, описує колову траєкторію. У цьому разі, однак, окрім доцентрового (або нормального) прискорення а_n тіло буде мати і тангенціальне прискорення а_τ. Тобто, повне прискорення тіла є векторною сумою цих двох складових. Аналізуючи взаємодію тіла з іншими тілами, доходимо висновку, що на тіло діють дві сили: сила тяжіння mg і сила реакції опори N (рис.8). Отже, саме рівнодійна цих двох сил і визначає повне прискорення тіла а при його русі по поверхні півкулі. 

 

                               

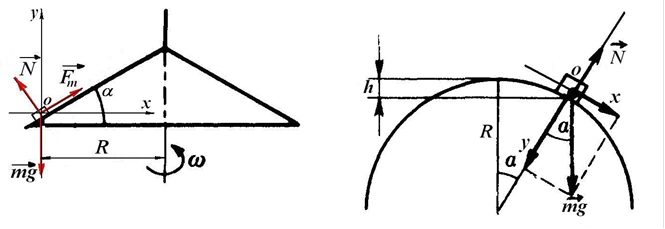
                                               Рис.7.                                                        Рис.8.

           

2.                 Інерціальну систему відліку зв’язуємо з нерухомою відносно землі кулею. Систему координат орієнтуємо таким чином, щоб напрям осі oy збігався з напрямом вектора доцентрового прискорення, а напрям осі ox з напрямом вектора миттєвої швидкості тіла у момент знаходження його на висоті h від вершини півкулі (рис.8). А тепер записуємо рівняння другого закону Ньютона у проекціях векторів сил і прискорення на вісь oy: 

                                                                    mg·cosα – N = ma_n .                                            (30)

Як бачимо, і у цьому разі фізична картина цілком зрозуміла і без використання поняття «доцентрова сила»: величину доцентрового прискорення тіла визначає алгебраїчна сума проекцій сил mg і N на вісь oy. З рис.8 зрозуміло, що cosα = (R –

h)/R. Тому рівняння (30) запишемо у такому вигляді:

                                                                    mg·(R – h)/R – N = (mv²)/R,                                (31)

де v – лінійна швидкість руху тіла у момент знаходження його на висоті h від вершини півкулі. Цю швидкість найпростіше знайти, використавши закон збереження повної механічної енергії. Отже, зміна потенціальної енергії тіла при його русі по поверхні півкулі за модулем дорівнює зміні кінетичної енергії:

                                                                    mgh = (mv²)/2.                                                    (32)

Звідси mv² = 2∙mgh. Підставляючи цей вираз у (31), одержимо таке рівняння:

                                                                    mg·(R – h)/R – N = 2∙mgh/R.                              (33)

З (33) і знаходимо силу реакції опори N, яка за третім законом Ньютона дорівнює за модулем шуканій силі тиску тіла на поверхню півкулі:

                                                                    N = mg·(R – 3∙h)/R.                                             (34)

Відповідь на друге питання, поставлене в задачі, очевидна: у момент відриву тіла на певній висоті h₁ від вершини кулі реакція опори N = 0. Тому, з формули (34) одержимо:  

mg·(R – 3∙h₁)/R = 0,

і, відповідно, h₁ = R/3.

 Отже, підсумовуючи розв’язки трьох останніх задач, можна констатувати, що і для прояснення фізичної суті задачі, і для самого розв’язування введення  поняття «доцентрова сила» є фізично необґрунтованим і зайвим.

   

Перелік посилань.

1.   Римкевич А.П. Збірник задач з фізики. – Х.: ББН, 2006. – 208 с. 

2.   Мясников С.П., Осанова Т.Н. Пособие по физике. – М.: Высшая школа, 1976. – 328 с.

3.   Сиротюк В.Д., Баштовий В.І. Фізика. Підручник для 10 класу середньої школи. –

К.: Освіта, 2010. – 303 с.

4.   Корсак К.В. Фізика. Письмовий екзамен: Посібник для вступників до вузів. – К.:

Либідь, 1992. – 224 с.