конференція «Обчислення числа Пі».

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Обчислення числа π

(Конференція до Міжнародного дня числа  π)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

План

 

1. Вступ
2. Історія свята числа Пі
3. Традиції на День числа Пі
4. Практична частина конференції

• Історія обчислень числа Пі;

     -   Практичні методи

      а) Найпростіші вимірювання;

      б) Вимірювання за допомогою зважування;

            в) Додавання площ прямокутників, вписаних у півкруг;

            г) Метод Монте – Карло.

    5. Заключна частина

     -   Цікаві факти про  число  Пі та День числа Пі;

     -   Музика числа "Пі"

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Вступ

 

       14 березня у світі щорічно відзначається одне з самих незвичайних свят - Міжнародний день числа «Пі». З цим числом ми стикаємося вже в молодших класах школи, коли починаємо вивчати коло. Число «Пі» - це математична константа, яка виражає відношення довжини кола до довжини його діаметра. В цифровому вираженні "Пі" починається як 3,141592... і має нескінченну математичну тривалість.

 

 

 

Історія свята числа Пі

 

Вперше День числа  Пі відзначили у 1988 році в науково-популярному музеї Експлораторіум в Сан-Франциско. Придумав його роком раніше фізик  Ларрі Шоу.

Дату 14 березня він вибрав не випадково, адже у загальному числі Пі цифри вказують на 3(третій місяць у році), а 14 – число березня. Фізик зробив все можливе, щоб святкові події на честь цього числа були настільки ж яскравими і значущими, як і інші свята.

 

 

Зазвичай свято розпочинається о 1:59 ночі, що разом з датою складає перші шість знаків числа π (3.14159).

      Окрім того, цей день (14 березня) є також і днем народження Альберта Ейнштейна, що надає йому додаткової значущості в очах математиків.

      Досконалий День Пі  стався 14-го березня 1592 року о 6 годині 53 хвилини та 58 секунд. Ця дата, записана в «американському» форматі, виглядає як 3/14/1592 6:53:58, що відповідає першим 12-ти знакам в числі π: 3.14159265358. Але, зважаючи на те, що того часу ще не було впроваджено ніякого стандартизованого відліку часу, тим більше з потрібною точністю, скоріше за все цей момент ніким не святкувався.

    Приблизний День пі є однією з двох дат: або 22 липня (записується 22/7 — цей дріб дорівнює 3.14, що є наближеним значенням π), або 26 квітня (25 квітня високосного року) — день, коли Земля проходить дві астрономічні одиниці по своїй орбіті з початку календарного року: в цей день загальна довжина орбіти Землі, поділена на довжину вже пройденої ділянки, дорівнює π (тобто Земля пройшла в цей момент по своїй орбіті 2 радіани).

 

День числа Пі – навіщо це свято?

   У першу чергу свято придумане для того, щоб проінформувати громадськість про історичні факти даного вимірювання та внести конкретику в знання всього світу про число Пі.

    Також День числа «Пі» відзначають для залучення уваги громадськості до важливості поняття при вивченні математиці, хоча б на елементарному побутовому рівні, і використання математичних знань у повсякденному житті.

 

Традиції на День числа Пі

 

        Традиційно цього дня випікаються торти круглої форми, а також пироги та інші кондитерські вироби. Проходять конкурси на ідеальне кругле творіння. Одним з головних критеріїв для участі у конкурсі є розміщення числа «Пі» у центрі свого шедевра.

         Особливу шану це свято має у математиків і фізиків. В цей день вони збираються за круглими столами та ведуть обговорення відносно даного незвичайного числа.

 

 

 

 

 

 

 

 

 

 

 

 

Число Пі повністю

 

 

Практична чистина конференції

 

Історія обчислень числа Пі

 

Відношення довжин кола до його діаметра є величина стала для всіх кіл. Вперше його позначив грецькою буквою π британець Вільям Джонс у праці «Огляд досягнень математики», надрукованій в 1706 році. Він керувався тим, що з неї починається слово περιμετρέο – «вимірюю навколо». Стара назва - лудольфове число, а загальноприйнятим воно стало після робіт  Леонарда Ейлера у 1748 році запропонував застосувати грецьку букву π (пі):

=π.

Таким чином, задача обчислення довжини кола С зводиться до обчислення числа π, так як С= π D= 2πR.

Число π є нескінченим неперіодичним десятковим дробом. Це було доведено тільки у 1882 році Ф.Ліндеманом, який показав, що число π трансцендентне, тобто воно не може бути коренем якого-небудь алгебраїчного рівняння.

Точне значення π (обмежуючись сорок одним знаком) буде

π = 3, 14159 26535 89793 23846 26433 83279 50288 41971...

Задача визначення довжини кола і площі круга, тобто задача обчислення числа π, привернула до себе увагу з давніх давен. Так, ще у єгиптян (2-ге тисячоліття до н.е.) π =3,1605, у вавилонців і давніх китайців π =3, у II ст. н.е. Чжан-Хен брав π = =3,162...

 

Ідея обчислення π як загальної границі вписаних і описаних правильних многокутників належить Архімеду (приблизно 287-212 р. до н.е.), який одержав оцінки

3< π <3

Взявши з оцінок їх середнє арифметичне, знайдемо π=3,14185, тобто визначимо π з похибкою меншою ніж 0,0003.

Користуючись методом Архімеда, французький математик Вієт обчислив 9 знаків π, Романус - 17, а Ван Цейлен - 32. Дальші обчислення вимагали великої праці і тому результат Ван Цейлена залишався рекордним, поки для обчислення π не були застосовані методи диференціального та інтегрального числення. Завдяки їм Ньютон (1643 - 1727) порівняно легко обчислив 14 знаків, а Ейлер (1707-1783)- 20, потім за допомогою нових формул Мешин (1706) одержав 100 знаків, Ріхтер (1855) - 500 і Шенкс (1874) - 707 знаків.

Нові можливості виникли після створення ЕОМ. У 1945 році за допомогою ЕОМ були перевірені обчислення Шенкса і виявилося, що у нього правильні тільки перші 528 знаків, а всі інші помилкові.

У 1949 році число π було обчислене з 2 000 знаків, а в 1957 році – з 10 000. Цікаво відмітити, що всі цифри у π (якщо розглядати досить їх велику кількість) зустрічаються однакову кількість разів, але ніякої закономірності у чергування цифр знайти не вдалося; вони слідують одна за одною безладно.

Обчислення такої великої кількості знаків у π велося головним чином з теоретичних інтересів; для самих складних розрахунків до нашого часу рідко використовують більше 10-15 десяткових знаків.

 

 

Практичні методи

 

1.   Найпростіші вимірювання.

      Накреслимо на цупкому картоні коло радіуса г, виріжемо одержаний круг і обмотаємо його тонкою ниткою. Вимірявши довжину l одного повного витка нитки, розділимо на довжину d діаметра кола. Одержана частка буде наближеним значенням π, тобто π = .

 

№	l	D	π
1	18,9	5,8	3,26
2	22,6	7,6	2,97
3	26,4	8,3	3,18
4	40,7	12,8	3,18
5	81,4	26,5	3,07

 

Такий досить грубий спосіб дає у звичайних умовах наближене значення π з точністю до 1.

2.   Вимірювання за допомогою зважування.

На аркуші картону накреслимо квадрат. Впишемо в нього круг. Виріжемо квадрат. Визначимо масу картонного квадрата за допомогою аптечних терезів. Виріжемо з квадрата круг. Зважимо його. Знаючи масу квадрата (m_кв) і вписаного в нього круга (m_кр), скористаємося формулами m=ρV, V=Sh, де ρ і h - відповідно густина і товщина картону, S-площа фігури. Розглянемо рівності:

m_кв =ρS=4ρR²h,     m_кр = ρS _кр h =ρ π R²h.

Звідси

m_кр : m_кв = , тобто π = 4 m_кр : m_кв.

 

mкв	mКр	π
0,85	0,65	3,06
1,3	1,0	3,08
13,7	10,66	3,09

Звичайно, у даному випадку наближене значення π залежить від точності зважування. Якщо картонні фігури, які зважуються, будуть досить великими, то можливо навіть на звичайних терезах одержати такі значення мас, які забезпечать наближення числа π з точністю до 0,1.

3.   Додавання площ прямокутників, вписаних у півкруг.

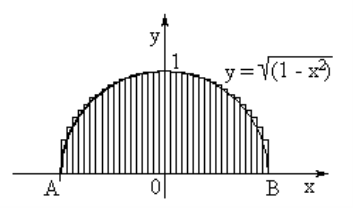         Нехай А(а,0), В(b,0). Опишемо на АВ півкруг як на діаметрі. Розділимо відрізок АВ на n рівних частин точками х₁, x₂, ..., х_n-1 і побудуємо з них перпендикуляри до перетину з півколом. Довжина кожного перпендикуляра - це значення функції  f(x)= . З малюнка 1 видно, що площа S півкруга обчислюється за формулою

S= (f(х₀)+f(x₁)+ ... +f(х_x-1)).

 

У нашому випадку видно, що b=1, а = -1. Тоді π ≈2S.

Значення π будуть тим точніші, чим більше точок поділу буде на відрізку АВ. Полегшити одноманітну роботу допоможе комп’ютер.

4.    Метод Монте - Карло.

Це метод статистичних випробувань. Свою назву він одержав від міста Монте-Карло в князівстві Монако, знаменитого своїми гральними будинками. Цей метод вимагає застосування випадкових чисел, а одним з найпростіших прикладів, які генерують випадкові числа, може бути рулетка. Хоча можна отримати випадкові числа і за допомогою дощу.

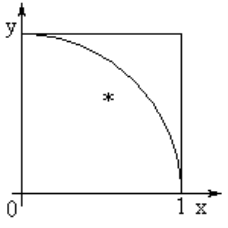Для досліду приготуємо аркуш картону, намалюємо на ньому квадрат і впишемо в нього чверть круга. Якщо таке креслення деякий час потримати під дощем, то на його поверхні залишаться сліди крапель. Порахуємо кількість слідів всередині круга і всередині квадрата. Очевидно, що їх відношення наближено дорівнює відношенню площ цих фігур, так як попадання крапель у різні місця креслення рівноймовірне. Нехай N _kp - кількість крапель у крузі, N_кв - кількість крапель у квадраті. Тоді

π ≈ 4N_кр : N_кв

      У методі Монте-Карло дощ можна замінити таблицею випадкових чисел, яка складається за допомогою комп’ютера за спеціальною програмою (можна використати одну з надрукованих у літературі таблиць).

Цікаві факти про День числа Пі

• Дивний марафон, розпочатий Архімедом, сьогодні так само далекий від завершення, як і дві тисячі років назад. У Книгу рекордів Гіннеса потрапив результат професора Григорія Чудновського із США, до речі, випускника Київського університету. Йому першому в світі вдалося перевершити рубіж в мільярд знаків! Проте рекорд протримався недовго, і співробітники Токійського університету Я.Канада і Д.Такахаші підняли планку до висоти — 206 мільярдів знаків. Але виявилось, що і це - ще не межа. 2 серпня 2010 року американський студент Олександр Йі і японський дослідник Сігеру Кондо знайшли 5 трильйонів цифр, а приблизно через рік, 19 жовтня 2011 року вони ж поліпшили свій результат – знайшли 10 трильйонів цифр числа пі.
  Чи зупиниться коли-небудь ця дивна гонитва за зникаючими в нескінченності знаками числа «пі»? Мабуть, це питання можна переформулювати так: чи припинить будь-коли своє існування людська цивілізація?
• Пів життя Вільям Шенкс вираховував 707 цифр, однак виявилось, що останні 180 знаків у «хвості» виявились неправильними.
• Щороку у Всесвітній день числа «пі» фанати легендарного числа збираються в Інтернеті. Будь-який житель планети має змогу прийняти учать у глобальному проект «Pi-Hex». І це не проста забавка для комп’ютерних гурманів, а досить серйозний науковий проект.

•                  Дата свята збігається з днем народження одного з найвідоміших фізиків – Альберта Ейнштейна, а також з датою смерті у 2018 році відомого фізика сучасності Стівена Хокінга.

-   Значення числа «Пі» відіграє важливу роль при будівництві. Тому його намагалися отримати ще в доісторичні часи. Найточніше значення отримав відомий вчений Архімед, який жив у Давній Греції.

- Мнемоністи намагаються поставити рекорд із запам'ятовування послідовності знаків після коми числа «Пі». У Книзі рекордів Гіннесса зафіксовано рекорд, який поставив японець Хідеакі Томойорі. Він зумів відтворити без помилки послідовність у 40 тисяч знаків. На вивчення пішло понад 10 років.

- У послідовності знаків числа "Пі" немає логічних повторень, а це значить, що ця послідовність підпорядковується теорії хаосу.

- Про це число у 1998 році зняв фільм культовий режисер Даррен Аранофськи.

- Музику числа "Пі" можна почути завдяки таким музикантам, як Девід Макдональд. Він записав з допомогою фортепіано, як звучить число "Пі", якщо його взяти з точністю до 122 знаків після коми. Для цього кожному числу був привласнений свій порядковий номер на клавіатурі фортепіано з мінорною шкалою.

 

 

 

 

 

 

 

 

 

 

Число Пі символ