КОНКУРС ЗНАВЦІВ ТРИГОНОМЕТРІЇ
Мета проведення: закріпити знання з тригонометрії, розширити загальний й математичний кругозір учнів; підвищити їх інтерес до вивчення математики; розвивати логічне мислення та вміння слухати; виховувати наполегливість й волю, доброзичливе ставлення до суперників.
Учасники: учні 10 класу (учні ПТНЗ професія «Електрослюсар підземний, машиніст електровоза, машиніст підземних установок»).
Сценарій
позакласного заходу з математики
«Конкурс знавців тригонометрії»
Суббота О.О.,
викладач математики
Білозерського професійного
гірничого ліцею
Мета проведення: закріпити знання з тригонометрії, розширити загальний й математичний кругозір учнів; підвищити їх інтерес до вивчення математики; розвивати логічне мислення та вміння слухати; виховувати наполегливість й волю, доброзичливе ставлення до суперників.
Учасники: учні 10 класу (учні І курсу, професія «Електрослюсар підземний, машиніст електровоза, машиніст підземних установок»).
Форма проведення: конкурс на особисту першість або командна гра.
Час, відведений на проведення заходу: 45 хвилин.
Обладнання: роздатковий матеріал, призи для гравців і призи для вболівальників.
Структура заходу
- Привітання учасників (3 хвилини).
- Розминка (5 хвилин).
- «Знавці формул» (5 хвилин).
Конкурс для вболівальників (проводиться під час конкурсів № 2 та 3).
- «Знайди помилку» (5 хвилин).
- «Вгадай слово» (5 хвилин).
- «Справжні математики» (9 хвилин).
- «Слабка ланка» (8 хвилин).
- Підсумки конкурсу (5 хвилин).
Хід заходу
- Привітання учасників (3 хвилини).
- Розминка (5 хвилин).
Завдання. З окремих символів скласти тригонометричні формули.
І варіант
![]()
![]()
ІІ варіант
![]()
![]()
ІІІ варіант
![]()
![]()
- «Знавці формул» (5 хвилин).
Завдання. Продовжити тригонометричні формули. Роздрукований матеріал роздається гравцям. Вони швидко дописують формули.
Основні тригонометричні тотожності
1) sin2α +cos2α =
2) tgα =
3) ctgα =
4) tgαctgα =
5) 1 + tg2α =
6) 1 + ctg2α =
Формулы додавання
1) sin(α![]() β) =
β) =
2) cos(α![]() β) =
β) =
3) tg(α![]() β) =
β) =
Формули подвійного аргументу
1) sin2α =
2) cos2α =
3) tg2α =
Формули суми та різниці однойменних тригонометричних функцій
1) sinα + sinβ =
2) sinα – sinβ =
3) cosα + cosβ =
4) cosα – cosβ =
- «Знайди помилку» (5 хвилин).
Завдання. Знайти помилки в формулах та обчисленнях. Роздрукований матеріал роздається гравцям. Вони виправляють помилки червоною ручкою або олівцем.
-
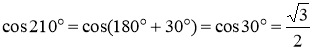
-
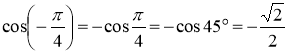
- sin2α – cos2α =1
-
1 + ctg2α =
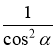
-
cosα =
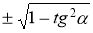
-
sin(α
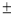 β) =
β) = 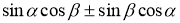
-
sin2α =
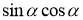
-
cos2α =
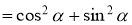
-
ctg2α =
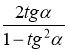
-
sinα + sinβ =
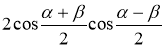
- «Вгадай слово» (5 хвилин).
Завдання. За підказками необхідно вгадати, про що мова. За відгадування за першою підказкою – 2 бали, за другою – 1,5 бали, за третьою – 1 бал, за четвертою – 0,5 бали. Викладач читає підказки. Гравці підіймають руку, якщо готові відповідати.
1 завдання (радіан).
- В перекладі з латинської мови це слово означає промінь.
- Кутова величина дуги, довжина якої дорівнює її радіусу.
- Основна одиниця вимірювання плоских кутів у сучасній математиці.
- Приблизно дорівнює 57 градусів.
2 завдання (період).
- Відрізок часу (або іншої величини), який визначається міткою початку та міткою кінця відліку часу.
- Його мають деякі десяткові дроби.
- Він є у деяких функцій.
- У функцій синус та косинус він дорівнює 2πn, а у тангенса та котангенса – πn, де n є Z.
3 завдання (теорема Піфагора).
- Її автори жили приблизно у 2300 році до н.е. у Стародавньому Єгипті.
- Вона допомогла нам одержати основні співвідношення між тригонометричними функціями одного аргументу.
- У науковій літературі зафіксовано 367 її доведень.
- Одне з її формулювань таке: «Піфагорові штани на всі сторони дорівнюють один одному».
4 завдання (область визначення).
- Вона є у всіх функцій.
- У синуса та косинуса вона співпадає з R.
-
У тангенса до неї не входять числа
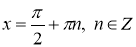 .
.
- Всі значення незалежної змінної х для даної функції.
- «Справжні математики» (9 хвилин).
Завдання. Спростити тригонометричний вираз. Роздрукований матеріал роздається гравцям. Учасники пишуть розв’язання.
-
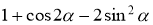 ;
;
-
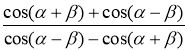 ;
;
-
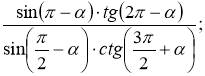
-
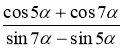 .
.
- «Слабка ланка» (8 хвилин).
Завдання. Гравцям необхідно по черзі відповідати на питання. Якщо гравець не надав правильну відповідь, право відповіді передається наступному гравцеві. Порядок опитування обирає викладач. Можна один за одним, як сидять.
Питання
- Дайте означення синуса гострого кута прямокутного трикутника.
- Назвіть знаки косинуса по чвертях.
- До якої чверті належить кут 320º?
- Яка з тригонометричних функцій є парною?
-
Назвіть
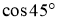 .
.
-
Продовжте формулу:
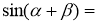
-
Продовжте формулу:
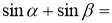
- Назвіть область визначення синуса.
-
Чи може
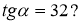
-
Продовжте формулу:
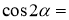
- Дайте означення косинуса гострого кута прямокутного трикутника.
- Дайте означення синуса довільного аргументу.
- Назвіть знаки тангенса по чвертях.
- До якої чверті належить кут 740º?
- Чому дорівнює період синуса та косинуса?
-
Назвіть
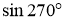 .
.
-
Продовжте формулу:
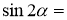
-
Продовжте формулу:
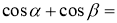
-
Чи може
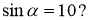 Чому?
Чому?
- Назвіть область значений косинуса.
- Сформулюйте правило отримання формул зведення.
- Дайте означення тангенса гострого кута прямокутного трикутника.
- Дайте означення косинуса довільного аргументу.
- Назвіть знаки синуса по чвертях.
- До якої чверті належить кут -245º?
- Назвіть непарні тригонометричні функції.
- Чому дорівнює період тангенса и котангенса?
-
Назвіть
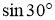 .
.
-
Назвіть
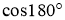 .
.
-
Продовжте формулу:
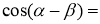
-
Продовжте формулу:
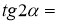
Конкурс для вболівальників (проводиться під час конкурсів № 2 та 3).
- Канат розтягується на 5 мм від навантаження в 100 кг. На скільки см він розтягнеться від навантаження в 10 тонн? (Розірветься)
-
Чи може дріб, у якому чисельник менше знаменника, бути рівним дробу, у якого чисельник більше знаменника?
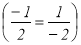
- Чому загадки небезпечні? (Головоломки)
- Коли ми дивимося на цифру 2, а говоримо : «Десять»? (На годиннику)
- На яке запитання не можна дати позитивної відповіді? («Ти спиш?»)
- У трьох малярів був брат Полікарп, а в Полікарпа братів не було. Як це могло бути? (Малярі - жінки)
- Син мого батька, а мені не брат. Хто це? (Я сам)
- Кавун коштує 1 гривню плюс ще пів-ціни кавуна. Скільки коштує кавун?
- (2 гривні)
- Три курки за 3 дні знесли 3 яйця. Скільки яєць знесуть 12 курей за 12 днів? (48 штук)
- На озері розцвіла чарівна лілія. Щодня число квіток подвоювалося, і на 20-тий день все озеро було покрито квітами. На який день була покрита половина? (на 19-тий).
Критерії оцінювання
|
За кожну правильну формулу – 1 бал. |
|
За кожну правильну формулу – 1 бал. |
|
За кожне правильне виправлення – 1 бал. |
|
За відгадування за першою підказкою – 2 бали, за другою – 1,5 бали, за третьою – 1 бал, за четвертою – 0,5 бали. |
|
За кожне правильне спрощення – 3 бали. |
|
За кожну правильну відповідь – 1 бал. |
Зауваження: якщо гравців багато, а час обмежений, можна оцінювати роботи після заходу, але для цього треба, щоб учні підписували свої роботи. Тоді результати будуть оголошені під час наступного уроку. Крім того, роздавальний матеріал треба мати в необхідній кількості.
Якщо ж гра командна, то можна оцінювати команди відразу, для чого запросити в журі інших викладачів або учнів старших курсів.
Зведена відомість
|
№ п/п |
Прізвище та ім’я учня |
Клас |
1.Розминка |
2.Знавці формул |
3.Знайди помилку |
4.Вгадай слово |
5.Справжні математики |
6.Слабка ланка |
Загальна сума балів |
|
1 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
11 |
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
13 |
|
|
|
|
|
|
|
|
|
|
14 |
|
|
|
|
|
|
|
|
|
|
15 |
|
|
|
|
|
|
|
|
|
|
16 |
|
|
|
|
|
|
|
|
|
|
17 |
|
|
|
|
|
|
|
|
|
|
18 |
|
|
|
|
|
|
|
|
|
|
19 |
|
|
|
|
|
|
|
|
|
|
20 |
|
|
|
|
|
|
|
|
|
|
21 |
|
|
|
|
|
|
|
|
|
|
22 |
|
|
|
|
|
|
|
|
|


про публікацію авторської розробки
Додати розробку
