Методичні рекомендації до спецкурсу "Розв'язування рівнянь з параметрами"
Традиційно розв'язування різного виду задач вважалось і предметом навчання математики, і ефективним засобом формування математичних знань і вмінь, інтелектуального розвитку і виховання учнів. В останні роки в шкільній практиці навчання математики спостерігається значний інтерес до задач з параметрами, оскільки вони представляють високу діагностичну і прогностичну цінність, за допомогою них можна перевірити знання основних розділів шкільної математики, володіння певним набором методів та ідей, рівень логічного мислення, навички дослідницької діяльності.
В посібнику поданий теоретичний матеріал до факультативного курсу «Розв'язування задач з параметрами» ( автор Апостолова В. Г.), наведені зразки розв'язання задач, подані вправи для домашнього завдання а також зразки залікових робіт.Для вчителів математики, учнів.
УПРАВЛІННЯ ОСВІТИ ЛУЦЬКОЇ МІСЬКОЇ РАДИ
КОМУНАЛЬНИЙ ЗАКЛАД «ЛУЦЬКА ГІМНАЗІЯ №4
ІМЕНІ МОДЕСТА ЛЕВИЦЬКОГО
ЛУЦЬКОЇ МІСЬКОЇ РАДИ ВОЛИНСЬКОЇ ОБЛАСТІ»
Дудик Л. М.
Розв’язування задач з параметрами
(методичні рекомендації для курсу за вибором
для 8 класу за програмою Апостолової В.Г.)
ЛУЦЬК – 2015
Рекомендовано до друку колегією науково – методичного центру
Луцької гімназії №4 імені Модеста Левицького
( протокол №5 від 12 лютого 2015 року)
Дудик Л. М.
Розв’язування задач з параметрами (методичні рекомендації) – 63 ст.
Традиційно розв’язування різного виду задач вважалось і предметом навчання математики, і ефективним засобом формування математичних знань і вмінь, інтелектуального розвитку і виховання учнів. В останні роки в шкільній практиці навчання математики спостерігається значний інтерес до задач з параметрами, оскільки вони представляють високу діагностичну і прогностичну цінність, за допомогою них можна перевірити знання основних розділів шкільної математики, володіння певним набором методів та ідей, рівень логічного мислення, навички дослідницької діяльності.
В посібнику поданий теоретичний матеріал до факультативного курсу «Розв’язування задач з параметрами» ( автор Апостолова В. Г.), наведені зразки розв’язання задач, подані вправи для домашнього завдання а також зразки залікових робіт.
Для вчителів математики, учнів.
Рецензенти:
С.Б. Гембарська – кандидат фізико-математичних наук, доцент кафедри диференціальних рівнянь і математичної фізики
Н.В. Шеретюк – голова методичного об’єднання вчителів математики Комунального закладу «Луцька гімназія №4 імені Модеста Левицького Луцької міської ради Волинської області»
ЗМІСТ
Вступ………………………………………………………………………………4
![]()
§2. Основна символіка теорії множин у записі математичних тверджень…..11
§3. Поняття про сімейство розв’язків рівняння відносно пквної змінної. Алгоритм розв’язування відносно ![]()
![]()
§4. Розв’язування лінійних рівнянь, що містять параметр у знаменнику……20
§5. Розв’язування системи двох лінійних рівнянь з параметрами……………22
§6. Раціональні рівняння з параметрами……………………………………….29
§7. Квадратні рівняння з параметрами…………………………………………34
§8. Рівняння, які зводяться до квадратних……………………………………..45
![]()
Залікова робота №1…………………………………………………………….59
Залікова робота №2……………………………………………………………..60
Список використаної літератури……………………………………………….62
ВСТУП
Бурхливий розвиток науки, техніки, інших галузей народного господарства неможливий без подальшого розвитку математики. Математичні методи та ідеї є провідними в багатьох галузях людської діяльності, тому підвищення рівня математичної освіти в Україні – одне з найважливіших завдань у роботі як вищої, так і середньої школи. Однак математична освіта в загальноосвітній школі спрямована в основному на засвоєння учнями алгоритмів розвязування типових навчальних задач, а цього недостатньо для потреб практики і розвитку здібностей до самостійного математичного мислення.
Одне з актуальних завдань сучасної школи — пошук нових шляхів зацікавлення учнів навчанням, підвищення їх розумової активності, спонукання до творчості, виховання школяра як життєво і соціально компетентної особистості, здатної здійснювати самостійний вибір і приймати відповідальні рішення в різноманітних життєвих ситуаціях, вироблення вмінь практичного і творчого застосування здобутих знань. Це означає, що вчитель у своїй діяльності має орієнтуватися на використання таких педагогічних технологій, з допомогою яких не просто поповнювалися б знання й уміння з навчального предмета, а й розвивалися такі якості учня, як пізнавальна активність, самостійність, уміння творчо підходити до виконання завдань.
Суспільство потребує висококваліфікованих фахівців з творчими здібностями. Тому навчальний процес повинен бути організований так, щоб випускники могли не лише адаптуватися в швидко змінному світі, але й були здатними до перетворення цього світу. Підготовка молоді до творчої праці неможлива без впровадження в навчальний процес сучасної школи навчально-дослідницької праці як важливого засобу формування в учнів стійкого інтересу й готовності до творчої діяльності. Сформовані на ранніх етапах навчання пізнавальний інтерес, творчі здібності, дослідницькі вміння є міцним фундаментом формування майбутніх кваліфікованих фахівців.
Під час орієнтування навчання на повномасштабне застосування дослідницьких методів слід враховувати, що схильність учнів до дослідницької діяльності в значній мірі індивідуальна. Вона виявляється у своєрідності розвитку їхніх пізнавальних інтересів, аналітичних здібностей, змісту й обсягу знань, спостережливості, пам'яті, уваги, гнучкості мислення, багатства уявлень, працьовитості, волі, спроможності до зосередженої й відповідальної праці. Застосування дослідницького підходу в навчанні спрямоване на становлення в школярів досвіду самостійного пошуку нових знань і використання їх в умовах творчості.
Отже, зміст шкільного курсу математики має містити такі питання, які б допомогли реалізувати творчий потенціал учнів, сприяли активному залученню до дослідницької діяльності з метою формування дослідницьких умінь. Таким матеріалом можуть стати, зокрема, задачі з параметрами.
Розв’язування таких вправ дозволяє повною мірою перевірити глибину знань основних розділів шкільної математики, з'ясувати рівень логічного мислення, первинні навики дослідницької діяльності учнів. Розв’язування задач з параметрами є одним із засобів реалізації наступності навчання у ланці "школа – ВНЗ". Проблеми, що виникають у школярів при розв’язуванні таких завдань викликані як їх відносною складністю, так і тим, що в школі, як правило, завданням з параметрами приділяється недостатня увага.
Задачи с параметрами майже не представлені в шкільному курсі математики. Між тим вони зустрічаються на підсумковій атестації та на ЗНО. Для розв’язування задач с параметрами не вимагається володіння знаниями, які виходять за рамки шкільної програми. Однак незвичність формулювання бентежить учнів, які не мають досвіду розв’язування подібних задач.
Задачі з параметрами – це по суті тест на перевірку рівня математичної культури, на її присутність чи відсутність.
Розв’язуванню задач з параметрами, як правило, присвячують заняття факультативів та курсів за вибором.
Питання організації факультативів з математики завжди залишалося в центрі уваги методичних досліджень. Це пов’язано з важливою роллю, яка припадає саме на факультативи в розвитку творчої особистості учня, завдяки можливістю врахування психологічних особливостей талановитих учнів під час таких занять.
В той же час, організації факультативів для учнів класів з поглибленим вивченням математики присвячена незначна кількість досліджень. Але досвід функціонування таких класів та фізико-математичних профільних навчальних закладів показує, що такі факультативи стають однією з головних ланок у системі освіти учнів класів з поглибленим вивченням математики. Той факт, що учні опинились у математичному класі, ще не завжди свідчить про зацікавленість учнів математикою, яка має тенденцію різко спадати, особливо при зростанні навчального навантаження на учнів та посилення складності завдань. Тому першою метою роботи факультативів повинна стати підвищення мотивації навчання. Ця мета повинна досягатися, перш за все, завдяки популяризації математичних знань та застосувань математики з одного боку, з іншого, спрямованістю факультативу на самореалізацію творчої особистості.
У посібнику подано методичні рекомендації до факультативного курсу «Розв’язування задач з параметрами» для 8 класу за програмою Г.В. Апостолової .
Метою курсу є поглиблення й розширення знань учнів з певних тем шкільного курсу математики, формування в них умінь й навичок розв’язування більш складних і різноманітних задач, що сприятиме подальшому успішному складанню відповідного рівня вступних випробувань (зовнішнього незалежного оцінювання) та майбутньому навчанню у технічних вищих навчальних закладах.
Задачі з параметрами традиційно входять до завдань вступних іспитів з математики до вищих навчальних закладів (зовнішнього незалежного оцінювання) з метою перевірки рівня логічного й абстрактного мислення абітурієнтів, здатності до аналізу й узагальнення, необхідних для подальшого
навчання у технічних вищих навчальних закладах.
Розв'язування задач з параметрами вимагає певного рівня розвитку відповідних типів мислення. Формування у школярів здатності до роботи з такими завданнями вимагає часу й послідовної методичної роботи вчителя. Останнє майже неможливо здійснити під час вивчення програмного матеріалу або на позакласних заняттях з підготовки до зовнішнього оцінювання в останній рік навчання в школі.
Завдання курсу — поступова адаптація учнів до розв'язування задач з параметрами, формування в них елементарних навичок роботи з відповідними завданнями, мислення розгалуження, а пізніше й пошукового абстрактного мислення, вміння моделювати та лаконічно і прозоро записувати розв'язання таких задач.
Орієнтовний розподіл навчального часу
|
№ уроку |
Тема уроку |
|
1,2 |
Систематизація та узагальнення основних понять про функцію. Розв’язування рівнянь виду |
|
3,4 |
Основна символіка теорії множин у записі математичних тверджень. |
|
5-7 |
Алгоритм розв’язування відносно |
|
8-11 |
Розв’язування лінійних рівнянь, що містять параметр у знаменнику. |
|
12-14 |
Розв’язування системи двох лінійних рівнянь з параметрами. |
|
15 |
Залікова робота |
|
16-19 |
Раціональні рівняння. Розв’язування рівнянь з параметрами, що зводяться до лінійних. |
|
20 |
Алгоритм розв’язування відносно
|
|
21-23 |
Квадратні рівняння з параметрами. |
|
24-28 |
Рівняння з параметром, які зводяться до квадратних. |
|
29-33 |
Співвідношення між коренями квадратного рівняння. |
|
34 |
Залікова робота. |
|
35 |
Підсумковий урок. |
Правило, за допомогою якого за кожним значенням незалежної змінної можна знайти єдине значення залежної змінної, називають функцією, а відповідну залежність однієї змінної від другої – функціональною.
Зазвичай незалежну змінну позначають буквою ![]()
![]()
![]()
![]()
![]()
![]()
Незалежну змінну ще називають аргументом функції.
Для функції ![]()
![]()
![]()
![]()
Усі значення, яких набуває аргумент, утворюють область визначення функції. Усі значення, яких набуває залежна змінна, утворюють область значень функції.
Функція вважається заданою, якщо вказано її область визначення і правило, за допомогою якого можна за кожним значенням незалежної змінної знайти значення залежної змінної.
Оскільки функція – це правило, то її можна задати за допомогою речень. Такий спосіб задання функції називають заданням функції описом.
Найпоширенішим способом задання функції є задання за допомогою формули.
Ще одним способом задання є табличний. Усі числа, записані в першому рядку таблиці, складають область визначення даної функції; у другому рядку записують відповідні значення функції.
Графіком функції ![]()
![]()
Коли якась фігура є графіком функції ![]()
1) якщо ![]() – деяке значення аргументу, а
– деяке значення аргументу, а ![]() – відповідне значення функції, то точка з координатами (
– відповідне значення функції, то точка з координатами (![]() ;
;![]() ) обов’язково належить графіку;
) обов’язково належить графіку;
2) якщо (![]() ;
; ![]() ) – координати довільної точки графіка, то
) – координати довільної точки графіка, то ![]() і
і ![]() – відповідні значення незалежної та залежної змінних функції
– відповідні значення незалежної та залежної змінних функції ![]()
![]() =
=![]()
![]() .
.
Фігура може бути графіком деякої функції, якщо будь-яка пряма, перпендикулярна до осі абсцис, має з цією фігурою не більше за одну спільну точку.
Рекомендовані вправи для розв’язання в класі і для домашнього завдання.
1. Дано функцію

Знайдіть ![]()
![]()
![]()
![]()
![]()
![]()
2. Не виконуючи побудови, знайдіть координати точок перетину з осями координат графіка функції:
1) ![]() 3)
3) ![]()
2) ![]() 4)
4) ![]()
3. Побудуйте графік функції, якщо відомо, що для всіх цілих значень аргументу значення функції дорівнює 1, а для нецілих дорівнює –1.
4. Графік функції ![]()
![]()
5. Графіки функцій ![]()
![]()
![]()
![]()
6. Побудуйте графік функції ![]()
7. При якому значенні ![]()
![]()
8. Побудуйте графік рівняння:
1) ![]()
2) ![]()
Поняття множини є одним з початкових математичних понять. Під множиною розуміють будь-яку сукупність, будь-який набір певних елементів. Об’єкти, з яких складається множина, називають її елементами. Запис ![]()
![]()
![]()
![]()
![]()
![]()
![]()
Найчастіше множину задають одним із таких двох способів.
Перший спосіб полягає в тому, що вказують всі її елементи. Записують це так ![]() . Але не кожну множину можна так задати. Наприклад, множину парних чисел так задати не можна.
. Але не кожну множину можна так задати. Наприклад, множину парних чисел так задати не можна.
Другий спосіб полягає в тому, що задається характеристична властивість елементів множини, тобто властивість, яка притаманна всім її елементам і тільки їм. Якщо ![]()
![]()
![]() . Після вертикальної риски вказують умову, якій має задовільняти елемент
. Після вертикальної риски вказують умову, якій має задовільняти елемент ![]()
![]()
Наприклад,
![]() – множина натуральних чисел, кратних 3;
– множина натуральних чисел, кратних 3;
![]() – множина коренів рівняння
– множина коренів рівняння ![]() . Ця множина дорівнює множині
. Ця множина дорівнює множині ![]() , яку, в свою чергу можна задати за допомогою іншої характеристичної властивості:
, яку, в свою чергу можна задати за допомогою іншої характеристичної властивості:
![]() .
.
Дві множини називаються рівними, якщо вони складаються з одних і тих же елементів. В останньому прикладі ![]()
Множину ![]()
![]()
![]()
![]()
![]()
Перетином множин ![]()
![]()
![]()
Перетин множин ![]()
![]()
![]()
![]() . Якщо множини
. Якщо множини ![]()
![]()
Об’єднанням множин ![]()
![]()
![]()
Об’єднання множин ![]()
![]()
![]()
![]() .
.
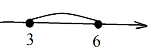
Розглянемо нерівність ![]()
![]()
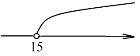
Нерівності ![]()
![]() .
.
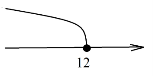
Точки, координати яких задовольняють нерівність ![]()
![]() називають числовим відрізком.
називають числовим відрізком.
Рекомендовані вправи для розв’язання в класі і для домашнього завдання.
1. Запишіть множину розв’язків рівняння:
1) ![]() ; 2)
; 2) ![]()
2. Запишіть переліком елементів множину:
1) ![]() ; 2)
; 2) ![]() .
.
3. Чи рівні множини ![]()
1) ![]()
![]() ;
;
2) ![]() ,
, ![]() .
.
4. Знайдіть перетин множин ![]()
1) ![]() ,
, ![]()
![]()
2) ) ![]() ,
, ![]() .
.
5. Знайдіть об’єднання множин ![]()
1) ![]() ,
, ![]() ;
;
2) ![]() ,
, ![]() .
.
6. Запишіть усі цілі числа, які належать проміжку:
1) ![]() ; 3)
; 3) ![]() .
.
7. Зобразіть на координатній прямій і запишіть перетин проміжків:
1) ![]() і
і ![]() ; 4)
; 4) ![]() і (2,8; +
і (2,8; +![]()
2) ![]() і (3;8); 5) (9; +
і (3;8); 5) (9; +![]()
![]()
3) ![]() і (2,5; +
і (2,5; +![]()
![]() і
і ![]()
8. Відомо, що ![]()
1) (m;n); 2) (k;p); 3) (n;k); 4) (m;p)?

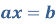
Нехай задане рівняння ![]()
Якщо ставиться задача відшукати всі такі пари ![]() , які задовольняють дане рівняння, то це рівняння з двома змінними
, які задовольняють дане рівняння, то це рівняння з двома змінними![]()
![]()
![]()
![]() можна розглядати як рівняння з однією змінною
можна розглядати як рівняння з однією змінною ![]()
![]()
Якщо ставиться задача для кожного значення ![]()
![]()
![]() відносно
відносно ![]()
![]()
![]()
![]()
Рівняння ![]() – це, по суті, короткий запис сімейства рівнянь. Так, рівняння
– це, по суті, короткий запис сімейства рівнянь. Так, рівняння ![]() , в якого область зміни параметра є множина
, в якого область зміни параметра є множина ![]() , є короткий запис наступного сімейства рівнянь:
, є короткий запис наступного сімейства рівнянь:
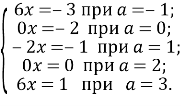
Домовимося надалі під областю зміни параметра розуміти (якщо немає ніяких зауважень) множину всіх дійсних чисел, а задачу розв’язання рівняння з параметром формулювати таким чином: Розв’язати рівняння ![]() (із змінною
(із змінною ![]()
![]()
![]() при всіх дійсних значеннях параметра.
при всіх дійсних значеннях параметра.
Зрозуміло, що виписати кожне рівняння із нескінченного сімейства рівнянь неможливо. Проте кожне рівняння сімейства повинно бути розв’язаним. Зробити це можливо, якщо, наприклад, за деякою доречною ознакою розбити множину всіх значень параметра на підмножини і розв’язати потім задане рівняння на кожній із цих підмножин.
Для розбиття множини значень параметра на підмножини зручно скористуватися тими значеннями параметра, при яких або при переході через які відбуваються якісні зміни рівняння. Такі значення параметра будемо називати контрольними.
 Розглянемо рівняння ax=b, де х – зміна, а і b – числа. При розв’язуванні лінійного рівняння ax=b зручно здійснювати за такою схемою
Розглянемо рівняння ax=b, де х – зміна, а і b – числа. При розв’язуванні лінійного рівняння ax=b зручно здійснювати за такою схемою
Приклад 1. Розв’язати рівняння ![]()
Розв’язання.
Тут контрольними будуть ті значення параметра, при яких коефіцієнт при змінній ![]()
![]()
![]()
![]()
![]()
![]() і розв’язати рівняння на кожній із цих підмножин. Розглянемо ці випадки.
і розв’язати рівняння на кожній із цих підмножин. Розглянемо ці випадки.
1) При ![]()
![]()
2) При ![]()
![]()
3) При ![]()
![]()
![]() .
.
Відповідь: якщо ![]()
![]()
![]()
![]() то
то ![]()
Приклад 2.
При якому значенні параметра ![]()
![]() має безліч розв’язків?
має безліч розв’язків?
Розв’язання.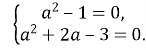 Звідки
Звідки 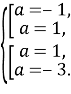 Отже,
Отже, ![]()
Відповідь: ![]()
Приклад 3.
При якому значенні параметра ![]()
![]() не має розв’язку?
не має розв’язку?
Розв’язання. Перетворивши дане рівняння, маємо ![]()
Останнє рівняння не має розв’язку. Якщо ![]()
Звідки 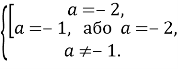 Отже,
Отже, ![]()
Відповідь: ![]()
Приклад 4. Дано рівняння ![]()
а) Для яких значень а рівняння не має коренів?
б) Чи існують значення а, для яких рівняння має більше, ніж один корінь?
Розв’язання.
а) Виконаємо тотожні перетворення даного рівняння та приведемо його до виду ![]()
![]()
![]()
Якщо ![]()
якщо ![]() і тоді рівняння має один корінь.
і тоді рівняння має один корінь.
Відповідь: а) при а=8 рівняння не має розв’язку,
б) не існує значення а, для яких рівняння має більше, ніж один корінь.
Приклад 5. Розв’язати рівняння ![]()
Розв’язання.
Перетворимо рівняння: ![]()
Якщо ![]()
![]() .
.
Якщо ![]()
![]()
а) якщо ![]()
![]()
б) якщо ![]()
![]()
![]()
Відповідь: якщо ![]()
![]() ; якщо
; якщо ![]()
![]()
![]()
![]()
Приклад 6. При яких значеннях t рівняння ![]()
Розв’язання.
![]()
![]()
Оскільки ![]()
![]() ; +
; + ![]()
Приклад 7. Визначити, при яких значеннях параметра ![]()
![]() має корінь, більший ніж 1.
має корінь, більший ніж 1.
Розв’язання. ![]()
![]()
Відповідь: ![]()
Приклад 8. При яких значеннях ![]()
![]() має єдиний розв’язок?
має єдиний розв’язок?
Розв’язання. Перетворивши рівняння, маємо:![]() . Дане рівняння має єдиний розв’язок, якщо
. Дане рівняння має єдиний розв’язок, якщо ![]()
Відповідь: ![]()
Приклад 9. Знайти всі цілі корені рівняння ![]()
![]()
Розв’язання. Перетворимо рівняння: ![]() .
.
Оскільки ![]()
![]() . За умовою корені повинні бути кратні 3, тобто
. За умовою корені повинні бути кратні 3, тобто
![]() , де
, де ![]()
![]() .
.
Відповідь: ![]() для
для ![]()
Приклад 10.
Для яких натуральних значень параметра ![]()
![]()
Розв’язання. Перетворимо рівняння: ![]()
![]()
![]()
![]() – непарне число. Оскільки
– непарне число. Оскільки ![]()
![]()
Відповідь: ![]()
![]()
Приклад 11. Розв’язати рівняння ![]() .
.
Розв’язання. Маємо: ![]() . Якщо
. Якщо ![]()
![]() .
.
Якщо ![]()
![]()
Відповідь: при ![]()
![]() ; при
; при ![]()
![]()
Приклад 12.
Розв’язати рівняння відносно змінної ![]() .
.
Розв’язання. Маємо: ![]() звідки
звідки ![]()
При будь-яких значеннях ![]()
Відповідь: при ![]()
![]()
![]()
Рекомендовані вправи для розв’язання в класі і для домашнього завдання.
1. Розв’яжіть рівняння:
1) 2![]()
![]()
![]()
2) ![]()
![]()
3) ![]() 6)
6) ![]()
7) ![]()
8) ![]()
9) (![]()
2. При якому значенні параметра ![]()
![]() має безліч розв’язків?
має безліч розв’язків?
3. При якому значенні параметра ![]()
![]() має безліч розв’язків?
має безліч розв’язків?
4. При якому значенні параметра ![]()
![]() не має розв’язку?
не має розв’язку?
5. При якому значенні параметра ![]()
![]() не має розв’язку?
не має розв’язку?
6. При яких значеннях ![]()
![]() має від’ємні розв’язки?
має від’ємні розв’язки?
7. При яких значеннях параметра ![]()
![]()
8. При яких значеннях параметра ![]()
![]() має корінь, більший за
має корінь, більший за ![]()
Відповіді:
1. 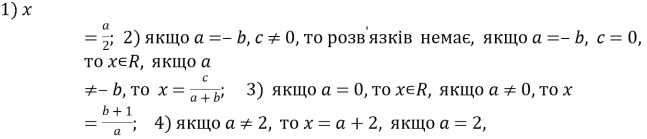 то
то ![]()
![]()
![]()
![]() 6)
6) ![]()
![]()
![]()
![]()
![]() 8) якщо
8) якщо ![]()
![]()
![]()
![]() ; 9) якщо
; 9) якщо ![]()
![]()
![]()
![]()
![]() . 2.
. 2. ![]()
![]()
4.![]()
![]()
![]() 7.
7. ![]() . 8.
. 8. ![]()

При розв’язуванні рівнянь з параметрами область зміни параметра може бути заданою. Якщо межі зміни параметра не задані, то вважається, що параметр набуває усіх своїх допустимих значень.
Приклад 1. Розв’язати рівняння ![]()
Розв’язання. Допустимі значення параметрів ![]()
![]()
тоді ![]()
1) Якщо ![]()
![]()
![]()
![]()
![]()
2) Якщо ![]()
![]()
![]()
![]() , яке не має коренів.
, яке не має коренів.
3) Якщо ![]()
![]()
![]()
Відповідь: якщо ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Приклад 2. Розв’яжіть рівняння ![]()
Розв’язання. Перепишемо рівняння у вигляді :
![]()
![]()
![]()
Оскільки жодна з величин ![]()
![]()
![]()
![]() =0.
=0.
Якщо ![]()
Якщо ![]()
![]()
![]()
Відповідь: якщо ![]()
![]()
![]()
![]()
Приклад 3. Розв’язати рівняння ![]() .
.
Розв’язання. Оскільки знаменник дробу не може дорівнювати нулю, то ![]()
![]()
Перетворимо рівняння: ![]() ,
, ![]() .
.
Для ![]()
-
Коефіцієнт при х дорівнює нулю, тобто
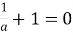 ,
, 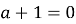
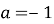
Тоді маємо рівняння: ![]()
-
Коефіцієнт при
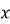
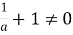 ,
, 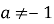
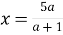 .
.
Відповідь: якщо ![]()
якщо ![]()
![]() .
.
Рекомендовані вправи для розв’язання в класі і для домашнього завдання.
Розв’язати рівняння:
1) ![]() 4)
4) ![]() ;
;
2) ![]() ; 5)
; 5) ![]()
3) ![]() 6)
6) ![]()
Відповіді: 1) якщо ![]()
![]()
![]() 2) якщо
2) якщо ![]()
![]()
![]() ; 3) якщо
; 3) якщо ![]()
![]()
![]()
4) якщо ![]()
![]()
![]() 5) якщо
5) якщо ![]()
![]()
![]() ; 6) якщо
; 6) якщо ![]()
![]()
![]() .
.
![]()
Системою двох лінійних рівнянь з двома невідомими ![]()
![]() де
де ![]() – довільні дійсні числа.
– довільні дійсні числа.
Дослідити систему означає за її коефіцієнтами встановити, який із нижче наведених випадків має місце:
1. Система має єдиний розв’язок (визначена).
2. Система не має розв’язку (несумісна).
3. Система має безліч розв’язків.
Система має єдиний розв’язок, якщо графіки рівнянь мають одну спільну точку, координати якої і є розв’язками даної системи.
Система не має розв’язків, якщо графіки рівнянь є взаємно паралельними прямими.
Система має безліч розв’язків, якщо графіки рівнянь збігаються (одна й та сама пряма).
Крім того система має єдиний розв’язок, якщо виконується умова ![]() , тобто коефіцієнти при відповідних невідомих не пропорційні між собою.
, тобто коефіцієнти при відповідних невідомих не пропорційні між собою.
В цьому випадку ![]()
Якщо ![]() , то розв’язків немає. При
, то розв’язків немає. При ![]() система має безліч розв’язків.
система має безліч розв’язків.
Приклад 1. Знайти, при яких значеннях параметра ![]()
![]() має безліч розв’язків, не має розв’язків.
має безліч розв’язків, не має розв’язків.
Розв’язання.
Система має безліч розв’язків, якщо ![]() Звідки
Звідки
![]() ;
; ![]()
Коли ![]()
![]() , тобто система має безліч розв’язків.
, тобто система має безліч розв’язків.
Коли ![]()
![]()
![]()
Відповідь: ![]()
![]()
Приклад 2. Знайти всі значення параметра ![]()
![]() не має розв’язків.
не має розв’язків.
Розв’язання. Дана система несумісна, тоді і тільки тоді, коли ![]() .
.
Із рівняння ![]() знаходимо
знаходимо ![]() .
.
Із рівняння ![]() знаходимо
знаходимо ![]() . Тобто умова
. Тобто умова ![]() виконується, якщо
виконується, якщо ![]()
Із системи 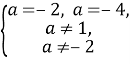 знаходимо,
знаходимо, ![]()
Відповідь: ![]()
Приклад 3. Визначити, при яких значеннях параметра ![]()
![]() не має розв’язку.
не має розв’язку.
Розв’язання. Система не має розв’язку, якщо ![]() З рівняння
З рівняння ![]() маємо
маємо 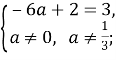 звідки
звідки ![]() . Перевіримо умову
. Перевіримо умову ![]() .
.
Підставивши в останній вираз замість ![]()
![]() , отримаємо:
, отримаємо: ![]()
Відповідь: ![]()
Приклад 4. Розв’язати систему рівнянь ![]()
Розв’язання. Домножимо перше рівняння на ![]()
![]() , звідки
, звідки ![]()
1) Якщо ![]()
![]() Отже,
Отже, ![]()
![]()
2) Якщо ![]()
![]() яка має безліч розв’язків виду (
яка має безліч розв’язків виду (![]() ), де
), де ![]()
3) Якщо ![]()
Відповідь: якщо ![]()
![]()
![]() , де
, де ![]()
![]()
![]()
![]()
![]()
![]()
Приклад 5. Для яких значень параметра ![]()
![]() має додатні розв’язки?
має додатні розв’язки?
Розв’язання. Домножимо перше рівняння на ![]()
![]() . Звідки, якщо
. Звідки, якщо ![]()
![]()
![]() .
.
Умова ![]()
![]()
Знайдемо значення ![]() +3
+3![]()
![]()
Умова ![]()
![]() , звідки
, звідки ![]() або
або ![]()
Отже, ![]()
![]()
![]() .
.
Відповідь: ![]() .
.
Приклад 6. Знайти всі значення параметра ![]()
![]()
![]()
![]() і нерівність
і нерівність ![]()
Розв’язання. Розв’язавши систему методом додавання, отримаємо
![]() .
.
За умовою ![]()
![]() , звідки
, звідки ![]()
Відповідь: ![]() .
.
Приклад 7. Для яких значень параметра ![]()
![]()
Розв’язання. Умову задачі можна переформулювати так: для яких значень параметра ![]()
![]() має єдиний розв’язок?
має єдиний розв’язок?
Очевидно, ![]() . Звідки
. Звідки ![]() .
.
Відповідь: ![]() .
.
Приклад 8. Розв’язати систему рівнянь ![]()
Розв’язання. З першого рівняння системи знайдемо значення ![]() .
.
Підставимо його в друге рівняння системи:
![]()
![]()
Розглянемо такі випадки.
1) Нехай ![]()
![]()
![]()
![]()
![]()
![]()
2) Нехай ![]()
![]()
3) Нехай ![]()
![]()
![]() .
.
Відповідь: якщо ![]()
![]()
![]() ;
;
якщо ![]()
![]()
![]()
![]()
![]()
Приклад 9. Дослідити і розв’язати систему ![]()
Розв’язання. Система має єдиний розв’язок, якщо ![]() ,
,
звідки ![]() . Знайдемо невідомі
. Знайдемо невідомі ![]()
![]()
![]() ;
; ![]() .
.
Дослідимо систему при ![]() .
.
Нехай ![]()
![]() тобто вона має безліч розв’язків виду
тобто вона має безліч розв’язків виду ![]()
![]()
Нехай ![]() , тоді маємо:
, тоді маємо: 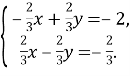 Дана система розв’язків не має.
Дана система розв’язків не має.
Відповідь: якщо ![]() , то
, то ![]() ;
; ![]()
якщо ![]()
![]()
![]()
![]() , то розв’язків немає.
, то розв’язків немає.
Рекомендовані вправи для розв’язання в класі і для домашнього завдання.
1. При якому значенні параметра![]()
![]() має безліч розв’язків?
має безліч розв’язків?
2. При якому найбільшому значенні параметра ![]()
![]() не має розв’язків?
не має розв’язків?
3. При яких значеннях m та n система рівнянь має безліч розв’язків ![]()
4. При якому значенні параметра![]()
![]()
5. Розв’язати систему рівнянь з параметром ![]()
![]()
6. Дослідити і розв’язати систему рівнянь ![]()
7. Дослідити і розв’язати систему рівнянь ![]()
8. При якому значенні параметра![]()
![]() має:
має:
а) єдиний розв’язок і знайти його; б) безліч розв’язків; в) не має розв’язків.
9. Дослідити і розв’язати систему рівнянь ![]()
10. При якому значенні параметра![]()
![]() має:
має:
а) єдиний розв’язок і знайти його; б) безліч розв’язків; в) не має розв’язків.
11. При яких значеннях m система рівнянь ![]() має додатні розв’язки?
має додатні розв’язки?
Відповіді:
1. ![]()
![]()
![]()
![]() 5. якщо
5. якщо ![]()
![]()
![]()
![]() ; 6. якщо
; 6. якщо ![]()
![]()
![]()
![]() 7. якщо
7. якщо ![]()
![]()
![]()
![]() 8. при
8. при ![]() ; при
; при ![]()
![]()
![]()
![]()
![]()
![]() ; 10. при
; 10. при ![]() при
при ![]()
![]()
![]()
![]()
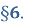
Приклад 1. Для кожного значення параметра ![]()
![]()
Розв’язання. Рівняння рівносильне системі ![]() Звідки
Звідки ![]()
Відповідь: якщо ![]()
![]()
![]()
Приклад 2. Для кожного значення параметра ![]()
![]() .
.
Розв’язання. Рівняння рівносильне системі ![]() Звідки
Звідки ![]()
Відповідь: якщо ![]()
![]()
![]()
![]()
![]()
![]()
Приклад 3. Для кожного значення параметра ![]()
![]()
Розв’язання. Рівняння рівносильне системі ![]()
Відповідь: якщо ![]()
![]()
![]()
![]()
![]()
Приклад 4. Для кожного значення параметра ![]()
![]()
Розв’язання. Рівняння рівносильне системі ![]()
При ![]()
![]()
Відповідь: якщо ![]()
![]()
![]()
Приклад 5. Для кожного значення параметра ![]()
![]()
Розв’язання. Рівняння рівносильне системі ![]()
При ![]()
![]()
![]()
При ![]()
![]()
![]()
При ![]()
![]()
![]()
Відповідь: якщо ![]()
![]()
![]()
![]()
![]()
![]()
![]()
Приклад 6. Для кожного значення параметра ![]()
![]()
Розв’язання. Маємо: ![]() Рівняння рівносильне системі
Рівняння рівносильне системі ![]()
![]()
Якщо ![]()
Якщо ![]()
![]()
Відповідь: якщо ![]()
![]()
![]()
![]()
Приклад 7. Для кожного значення параметра ![]()
![]()
Розв’язання. Маємо: ![]() =0;
=0; ![]() Рівняння рівносильне системі
Рівняння рівносильне системі ![]()
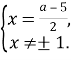
Рівняння не має коренів, якщо ![]() , тобто
, тобто ![]()
![]()
Відповідь: якщо ![]()
![]()
![]()
![]()
Приклад 8. Для кожного значення параметра ![]()
![]()
Розв’язання. Маємо: ![]() Рівняння рівносильне системі
Рівняння рівносильне системі 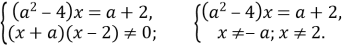
Рівняння не має розв’язків при![]()
![]()
![]() і при
і при ![]() Звідки
Звідки ![]()
![]()
![]()
![]()
![]() .
.
Відповідь: якщо ![]()
якщо ![]()
![]()
![]()
якщо ![]() .
.
Приклад 9. При яких значеннях параметра ![]()
![]() має єдиний розв’язок?
має єдиний розв’язок?
Розв’язання. Рівняння рівносильне системі ![]() Отже єдиний розв’язок
Отже єдиний розв’язок ![]()
![]()
Відповідь: ![]()
Приклад 10. При яких значеннях параметра ![]()
![]() має єдиний розв’язок?
має єдиний розв’язок?
Розв’язання. Рівняння рівносильне системі ![]()
Рівняння має єдиний розв’язок ![]()
![]()
![]()
якщо ![]()
![]()
![]()
![]()
Відповідь: при ![]()
![]()
![]()
Приклад 11. При яких значеннях параметра ![]()
![]() має єдиний розв’язок?
має єдиний розв’язок?
Розв’язання. Рівняння рівносильне системі ![]() Рівняння матиме єдиний розв’язок, якщо
Рівняння матиме єдиний розв’язок, якщо ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Відповідь: при ![]()
![]()
![]()
Приклад 12. Для кожного значення параметра ![]()
![]()
Розв’язання. Маємо: ![]() Рівняння рівносильне системі
Рівняння рівносильне системі ![]()
Якщо ![]()
Якщо ![]()
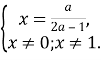
Знайдемо ті значення параметра ![]()
![]() дорівнює 0 або 1.
дорівнює 0 або 1. ![]() при
при ![]()
![]() при
при ![]()
![]()
![]()
Відповідь: якщо ![]()
![]()
![]()
![]()
![]()
![]()
![]()
Приклад 13. Розв’язати рівняння ![]()
Розв’язання. Область визначення даного рівняння ![]()
![]()
![]()
Якщо ![]()
![]()
Якщо ![]()
![]() З’ясуємо, для яких значень параметра
З’ясуємо, для яких значень параметра ![]()
![]()
![]()
Відповідь: якщо ![]()
![]() ;
;
якщо ![]()
Рекомендовані вправи для розв’язання в класі і для домашнього завдання.
1. Для кожного значення параметра ![]()
1) ![]() 4)
4) ![]()
2) ![]() 5)
5) ![]()
![]()
3) ![]() 6)
6) ![]()
2. При яких значеннях параметра ![]()
1) ![]() 2)
2) ![]()
Відповіді: 1. 1) якщо ![]()
![]()
![]()
2) якщо ![]() , то коренів немає, якщо
, то коренів немає, якщо ![]()
![]() то
то ![]()
3) якщо ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
5) якщо ![]()
![]()
![]()
![]() ;
;
6) якщо ![]()
![]()
![]()
![]()
![]()
2. 1) ![]() ; 2)
; 2) ![]()
![]()
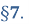
Рівняння виду ![]() – дійсні числа і
– дійсні числа і ![]()
![]() .
.
Якщо ![]()
![]()
Якщо ![]()
![]() , то рівняння має два дійсні корені.
, то рівняння має два дійсні корені.
Якщо ![]()
![]() , то рівняння має єдиний корінь
, то рівняння має єдиний корінь ![]() (іноді кажуть: два однакові корені).
(іноді кажуть: два однакові корені).
Якщо ![]()
![]() , то рівняння не має дійсних коренів.
, то рівняння не має дійсних коренів.
Для коренів ![]() квадратного рівняння виконується теорема Вієта
квадратного рівняння виконується теорема Вієта 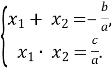
Приклад 1.
При якому значенні параметра ![]()
![]() має єдиний корінь?
має єдиний корінь?
Розв’язання. Розкривши дужки та звівши подібні доданки, отримаємо: ![]()
Останнє рівняння має єдиний розв’язок, якщо його дискримінант дорівнює нулю, тобто ![]()
Тоді ![]()
Відповідь: ![]()
Приклад 2. Розв’язати рівняння ![]()
Розв’язання. ![]()
Оскільки для будь-яких значень ![]()
![]()
![]()
![]()
Відповідь: ![]()
Приклад 3. Розв’язати рівняння ![]()
Розв’язання. Слід розглянути два випадки.
1) Для ![]()
![]()
2) Для ![]()
![]() Оскільки
Оскільки ![]()
![]()
![]() .
.
Відповідь: якщо ![]()
![]()
![]()
![]() .
.
Приклад 4. Розв’язати рівняння ![]()
Розв’язання. Оскільки ![]()
два випадки.
1) Якщо ![]()
![]()
2) Якщо ![]()
![]()
![]()
3) Якщо ![]()
![]() і отримаємо
і отримаємо
![]()
Якщо ![]() 0, тобто
0, тобто ![]()
![]() .
.
Якщо ![]() , тобто
, тобто ![]()
Якщо ![]() , тобто
, тобто ![]()
Відповідь: якщо ![]()
![]()
![]() ; якщо
; якщо ![]()
![]()
![]() .
.
Приклад 5. Знайти всі значення параметра ![]()
![]() має два різні корені.
має два різні корені.
Розв’язання. Оскільки за умовою рівняння має два різні корені, то воно є квадратним, отже, ![]()
![]()
![]() За умовою
За умовою ![]()
![]()
![]() . Тоді
. Тоді ![]() .
.
Відповідь: рівняння має два різні корені при ![]()
Приклад 6. Для яких значень параметра ![]()
![]() дорівнює нулю?
дорівнює нулю?
Розв’язання. За теоремою Вієта ![]()
Тоді ![]()
Але з того, ![]() , ще не випливає, що
, ще не випливає, що ![]() – дійсні корені. Потрібно, щоб виконувалася умова:
– дійсні корені. Потрібно, щоб виконувалася умова: ![]()
![]() Цю нерівність не обов’язово розв’язувати. Достатньо перевірити її виконання, якщо
Цю нерівність не обов’язово розв’язувати. Достатньо перевірити її виконання, якщо ![]() Перевіркою встановлюємо, що значення
Перевіркою встановлюємо, що значення ![]()
Відповідь: ![]()
Приклад 7. Для яких значень ![]()
![]() та
та ![]() мають принаймні один спільний корінь?
мають принаймні один спільний корінь?
Розв’язання. Якщо ![]()
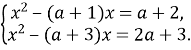 Віднімемо від першого рівняння друге:
Віднімемо від першого рівняння друге: ![]() . Підставимо значення
. Підставимо значення ![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Відповідь: ![]() .
.
Приклад 8. При скількох цілих значеннях параметра m сума коренів рівняння ![]() є в проміжку (
є в проміжку (![]()
Розв’язання. За теоремою Вієта ![]()
Тоді ![]() Звідки
Звідки ![]()
Отже, параметр набуває таких значень: 5; 6; 7; 8; 9.
Відповідь: 5.
Приклад 9. Для кожного значення параметра ![]()
![]() .
.
Розв’язання. Дане рівняння є квадратним. Кількість його розв’язків залежить від значення дискримінанта. ![]() ,
,
![]()
![]() .
.
Якщо ![]()
![]()
![]() .
.
Якщо ![]()
![]()
![]() ;
;
![]() ;
; ![]() ;
;
![]() .
.
Відповідь: якщо ![]()
![]() ;
;
якщо ![]()
![]() .
.
Приклад 10 . Розв’язати рівняння ![]()
Розв’язання. Дане рівняння має зміст при будь-яких дійсних значень параметра ![]()
1) Нехай ![]()
![]()
![]()
2) Нехай ![]()
![]()
![]()
3) Нехай ![]()
![]()
![]() ;
; ![]()
Тоді ![]() ;
; ![]() та
та ![]() .
.
Відповідь: коли ![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
, ![]() .
.
Приклад 11 . Розв’язати рівняння ![]()
Розв’язання. Дане рівняння має зміст при будь-яких дійсних значень параметра ![]()
1) Нехай ![]()
![]()
![]()
2) Нехай ![]()
![]() . Звідки:
. Звідки: ![]() .
.
Отже, при ![]() , рівняння не має дійсних коренів;
, рівняння не має дійсних коренів;
при ![]()
![]() .
.
Відповідь: ![]() , рівняння не має дійсних коренів; коли
, рівняння не має дійсних коренів; коли ![]()
![]() ; коли
; коли ![]() ,
, ![]() .
.
Приклад 12 . Розв’язати рівняння ![]()
Розв’язання. Нехай ![]()
![]()
Нехай ![]()
![]() =
= ![]()
Якщо ![]() , тобто
, тобто ![]() або
або ![]() , то рівняння має один корінь
, то рівняння має один корінь ![]() . При
. При ![]()
![]() ; при
; при ![]()
![]() .
.
Якщо ![]() , тобто
, тобто ![]() , то рівняння не має розв’язків.
, то рівняння не має розв’язків.
Якщо ![]() , тобто
, тобто ![]() , то рівняння має два корені
, то рівняння має два корені ![]() .
.
Відповідь: якщо ![]() , то рівняння розв’язків не має; якщо
, то рівняння розв’язків не має; якщо ![]() , то
, то ![]() ;
;
якщо ![]()
![]()
![]()
![]() ; якщо
; якщо ![]()
![]() .
.
Приклад 13 . Визначити, для яких значень ![]()
![]() буде найменшою.
буде найменшою.
Розв’язання. За теоремою Вієта маємо ![]()
![]() Згідно з умовою, знайдемо
Згідно з умовою, знайдемо ![]()
Вираз ![]() набуває найменшого значення, коли
набуває найменшого значення, коли ![]()
Але ![]() і для
і для ![]()
![]()
![]()
![]()
![]() набуває найменшого значення. Знайдемо, для яких значень
набуває найменшого значення. Знайдемо, для яких значень ![]()
![]()
![]() З усіх чисел, які належать даному об’єднанню проміжків, найближчим до 1 є
З усіх чисел, які належать даному об’єднанню проміжків, найближчим до 1 є ![]() .
.
Відповідь: ![]() .
.
Приклад 14 . ![]()
Розв’язання. Перетворимо рівняння: ![]() ;
;
![]() .
.
Нехай ![]()
![]()
Нехай ![]()
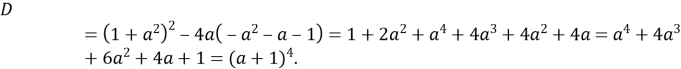
Якщо ![]()
![]()
![]()
Якщо ![]()
![]()
![]() ;
;
![]() ;
; ![]() .
.
![]() .
.
Відповідь: якщо ![]()
![]()
![]()
![]()
![]() .
.
Приклад 15 . Дослідити рівняння: ![]()
Розв’язання.
Нехай ![]()
![]() .
.
Нехай ![]()
![]()
![]()
Якщо ![]() , тобто
, тобто ![]() , то рівняння не має розв’язків.
, то рівняння не має розв’язків.
Якщо ![]() , тобто
, тобто ![]() , але
, але ![]()
![]() .
.
Відповідь: якщо ![]() , то рівняння розв’язків не має; якщо
, то рівняння розв’язків не має; якщо ![]()
![]() ;
;
![]() , але
, але ![]()
![]() .
.
Приклад 16 . Не розв’язуючи рівняння ![]() , знайти, для якого значення
, знайти, для якого значення ![]()
Розв’язання. Рівняння матиме два корені, якщо ![]()
![]() тобто
тобто ![]() .
.
За умовою ![]() За теоремою, оберненою до теореми Вієта, маємо:
За теоремою, оберненою до теореми Вієта, маємо: 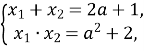
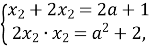
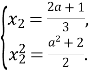
Отже, ![]()
![]() ,
, ![]() ,
, ![]()
Відповідь: ![]()
Приклад 17. Для яких значень параметра ![]()
![]() дорівнює їх добутку?
дорівнює їх добутку?
Розв’язання. За теоремою, оберненою до теореми Вієта, маємо: 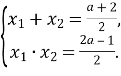
Оскільки 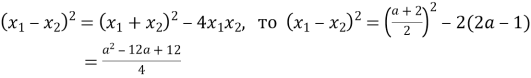 .
.
Отже, ![]() Рівність можлива, якщо
Рівність можлива, якщо ![]() , тобто
, тобто ![]() або
або ![]() .
.
За умовою ![]() , тому
, тому ![]()
Звідки ![]() Обидва значення
Обидва значення ![]()
![]()
Відповідь: ![]()
Приклад 18. Знайти всі значення параметра ![]()
![]() дорівнює 1.
дорівнює 1.
Розв’язання. За теоремою, оберненою до теореми Вієта, маємо: 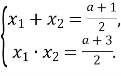 Оскільки
Оскільки ![]() .
.
За умовою ![]()
![]()
Оскільки рівняння має два дійсні корені, то ![]()
![]() ,
,
тобто ![]() Дану умову задовольняють всі знайдені значення
Дану умову задовольняють всі знайдені значення ![]()
Відповідь: ![]()
Приклад 19. Для яких значень параметра ![]()
![]()
Розв’язання. За теоремою, оберненою до теореми Вієта, маємо: 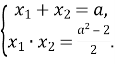 За умовою
За умовою ![]()
![]() .
.
Оскільки ![]() – дійсні корені заданого рівняння, то
– дійсні корені заданого рівняння, то ![]()
Знайдемо ![]() , звідки
, звідки ![]()
Знайдену умову задовольняє ![]() .
.
Відповідь: ![]()
Приклад 20. Для рівняння ![]() вказати таке значення
вказати таке значення ![]()
Розв’язання. За теоремою, оберненою до теореми Вієта, за умови
![]()
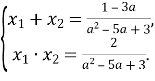
Нехай ![]() , а
, а ![]()
![]()
Тоді: 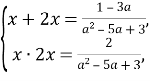
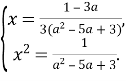
Отже, ![]()
Якщо ![]() то задане рівняння перетворюється у лінійне і має один корінь.
то задане рівняння перетворюється у лінійне і має один корінь.
Відповідь: ![]()
Приклад 21. Для рівняння ![]() вказати таке значення
вказати таке значення ![]()
![]() задовольняють умову
задовольняють умову ![]()
Розв’язання. За теоремою, оберненою до теореми Вієта, ![]()
Оскільки ![]() то
то ![]() Тоді
Тоді ![]() ,
,
7(![]()
![]()
Отже, ![]()
Відповідь: ![]()
Рекомендовані вправи для розв’язання в класі і для домашнього завдання.
1. Для кожного значення параметра ![]()
1) ![]() ;
;
2)![]() ;
;
3) ![]() .
.
2. При яких значеннях параметра ![]()
1) ![]() ;
;
2) ![]() ;
;
3) ![]()
4) ![]()
3. При яких значеннях параметра ![]()
1) ![]()
2) ![]()
4. При скількох цілих значеннях параметра ![]()
![]() є в проміжку
є в проміжку ![]()
5. У рівнянні ![]() визначити
визначити ![]()
![]() .
.
Відповіді:
1. 1) якщо ![]()
2) якщо ![]()
![]() ;
;
3) якщо ![]() ;
; ![]()
![]() .
.
2. 1) ![]() 2)
2) ![]() ;
;
3) ![]()
![]()
3. ![]()
![]()
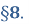
Приклад 1. Розв’язати рівняння ![]()
Розв’язання. Зрозуміло, що ![]()
![]()
![]() . Так як
. Так як ![]()
![]()
Якщо ![]()
![]()
Якщо ![]()
![]()
Обидва значення ![]()
![]()
Відповідь: якщо ![]()
якщо ![]()
![]()
![]()
Приклад 2. Розв’язати рівняння ![]()
Розв’язання. Дане рівняння має зміст при всіх значеннях ![]()
![]()
![]()
Якщо ![]()
![]() звідки на області допустимих значень параметра виконується умова
звідки на області допустимих значень параметра виконується умова ![]()
Дискримінант цього рівняння ![]() , а його корені
, а його корені ![]()
Враховуючи область допустимих значень невідомого, отримаємо:
![]()
![]()
![]()
![]()
![]()
![]()
Якщо ![]()
![]()
![]()
![]()
якщо ![]()
![]()
![]()
![]()
Відповідь:
якщо ![]()
![]()
якщо ![]()
![]()
![]()
![]()
якщо ![]()
![]()
![]()
![]()
Приклад 3. Розв’язати рівняння ![]()
Розв’язання. Виконаємо перетворення: ![]()
Рівняння рівносильне системі ![]()
Розв’яжемо рівняння ![]() .
.
Після перетворень матимемо: ![]() ;
;
![]()
Якщо ![]()
![]() , коренем якого є число
, коренем якого є число ![]()
Якщо ![]()
![]()
![]()
![]() .
.
Ці значення змінної будуть коренями даного рівняння тільки при виконанні таких умов: ![]() Очевидно, що умови 4
Очевидно, що умови 4![]()
![]()
Якщо ![]() , тобто
, тобто ![]()
![]()
![]()
![]() є стороннім. Разом з тим для
є стороннім. Разом з тим для ![]()
![]() і
і ![]() є коренем заданого рівняння.
є коренем заданого рівняння.
Якщо ![]() , тобто
, тобто ![]()
![]()
![]()
![]() є стороннім, а
є стороннім, а ![]() є коренем.
є коренем.
Відповідь: якщо ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Приклад 4. Для кожного значення параметра ![]()
![]()
Розв’язання. Рівняння рівносильне системі: ![]()
Розв’яжемо рівняння ![]()
![]() .
.
Якщо ![]() , то
, то ![]()
![]() ;
; ![]()
Оскільки при ![]()
![]()
![]()
![]() .
.
Визначимо значення ![]()
![]()
![]()
Отже, при ![]()
![]()
Відповідь: якщо ![]() , то
, то ![]()
![]()
![]() , то
, то ![]()
Приклад 5. Для кожного значення параметра ![]()
![]()
Розв’язання. Виконаємо перетворення: ![]() ;
;
![]() .
.
Рівняння рівносильне системі: 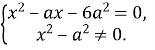
Розв’яжемо рівняння ![]() .
.
![]() .
.
Якщо ![]()
![]()
![]()
![]()
Якщо ![]()
![]() ;
; ![]() .
.
В цьому випадку виконується умова ![]()
Відповідь: якщо ![]()
![]()
![]()
![]()
Приклад 6. Для кожного значення параметра ![]()
![]()
Розв’язання. Виконаємо перетворення: ![]()
![]() .
.
Рівняння рівносильне системі: ![]()
Розв’яжемо рівняння ![]() .
.
![]()
Знайдемо, при якому значенні ![]()
![]()
![]()
Відповідь: якщо ![]()
![]()
якщо ![]()
![]()
![]()
Приклад 6. При яких значеннях параметра ![]()
![]() має один корінь?
має один корінь?
Розв’язання. Рівняння рівносильне системі: ![]()
Розв’яжемо рівняння ![]()
![]() .
.
Рівняння має один корінь, якщо ![]()
![]()
В першому випадку при ![]()
![]()
У другому випадку ![]()
Якщо ![]() , тобто
, тобто ![]()
![]() .
.
![]() не дорівнює 1 при жодному значенні
не дорівнює 1 при жодному значенні ![]()
Відповідь: ![]() або
або ![]()
Приклад 7. При яких значеннях параметра ![]()
![]() ?
?
Розв’язання.
Рівняння рівносильне системі: ![]()
Розв’яжемо рівняння ![]()
![]()
Якщо ![]()
![]()
![]() що не задовольняє умову
що не задовольняє умову ![]()
При ![]()
![]()
![]()
![]() .
.
Рівняння має один корінь, якщо ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Відповідь: ![]()
Приклад 8. Розв’язати рівняння ![]()
Розв’язання. Рівняння кубічне відносно змінної ![]()
![]()
Запишемо його у вигляді ![]() і розв’яжемо як квадратне рівняння відносно параметра
і розв’яжемо як квадратне рівняння відносно параметра ![]()
![]() , то
, то ![]()
Отже, дане рівняння рівносильне сукупності: ![]()
![]()
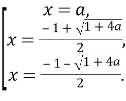 Останні дві рівності сукупності мають місце за умови
Останні дві рівності сукупності мають місце за умови ![]() .
.
Якщо ![]() , то
, то ![]() або
або ![]() .
.
Відповідь: якщо ![]() , то
, то ![]()
![]() , то
, то ![]() або
або ![]() ; якщо
; якщо ![]() , то
, то ![]()
![]() .
.
Приклад 9.
Скільки розв’язків має рівняння ![]() залежно від параметра
залежно від параметра ![]()
Розв’язання. Оскільки дане рівняння квадратне відносно ![]()
![]() і розв’яжемо відносно
і розв’яжемо відносно ![]()
За теоремою, оберненою до теореми Вієта: 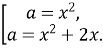
Перепишемо сукупність у вигляді: 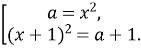
Тоді маємо: 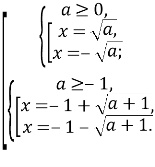
Відповідь: якщо ![]()
![]()
![]()
![]() , то
, то ![]() ; якщо
; якщо ![]()
![]()
![]() ; якщо
; якщо ![]()
![]()
![]()
Приклад 10. Розв’язати рівняння ![]()
Розв’язання. Якщо ![]()
![]() , яке не має дійсних коренів.
, яке не має дійсних коренів.
Нехай ![]()
![]() . Тоді дане рівняння рівносильне системі
. Тоді дане рівняння рівносильне системі ![]()
Перше рівняння має корені ![]()
Другий корінь не задовольняє умову ![]()
![]()
![]()
![]()
Тоді при ![]()
![]() .
.
Відповідь: якщо ![]()
якщо ![]()
![]() .
.
Рекомендовані вправи для розв’язання в класі і для домашнього завдання.
1. Для кожного значення параметра ![]()
1) ![]() 3)
3) ![]()
2) ![]() 4)
4) ![]()
2. При яких значеннях параметра ![]()
1) ![]() 3)
3) ![]()
2) ![]()
При розв’язуванні квадратних рівнянь, в яких потрібно дослідити значення коренів, слід пам’ятати такий навчальний матеріал.
Нехай дано квадратний тричлен ![]() . За теоремою Вієта якщо
. За теоремою Вієта якщо ![]() – корені квадратного тричлена
– корені квадратного тричлена ![]() , то має місце система
, то має місце система 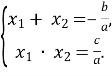
Теорема 1. Для того, щоб корені квадратного тричлена були дійсними і мали однакові знаки, необхідно і достатньо виконання таких умов: 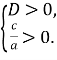
При цьому обидва корені будуть додатними, якщо додатково виконується умова ![]() , тобто
, тобто 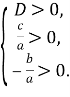
Обидва корені будуть від’ємними, якщо ![]() , тобто
, тобто 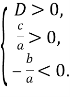
Теорема 2. Для того, щоб корені квадратного тричлена були дійсними і мали різні знаки, необхідно і достатньо виконання таких умов: 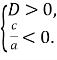
При цьому додатний корінь буде більшим за модулем, якщо ![]() тобто
тобто 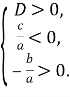
Від’ємний корінь буде більшим за модулем, якщо 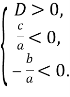
Теорема 3. Для того, щоб обидва корені квадратного тричлена були менші за число ![]()
![]()
для ![]()
![]()
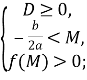

які також можна записати у вигляді однієї системи 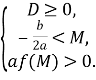
Теорема 4. Для того, щоб один із коренів квадратного тричлена був меншим за число ![]()
![]()
![]()
для ![]()
![]()
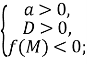

які виконуються також і тоді, коли ![]() .
.
Теорема 5. Для того, щоб обидва корені квадратного тричлена були більшими за число ![]()
![]()
для ![]()
![]()
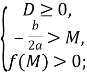

які також можна записати у вигляді однієї системи 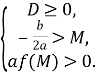
Наслідок 1. Для того, щоб обидва корені квадратного тричлена були більшими за число ![]()
![]()
![]()
![]()
для ![]()
![]()
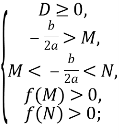
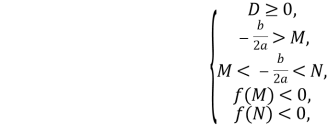
які також можна записати у вигляді однієї системи 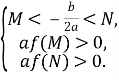
Наслідок 2. Для того, щоб тільки більший корінь квадратного тричлена лежав між числами ![]()
для ![]()
![]()
![]()
![]()
які можна записати також у вигляді однієї системи ![]()
Наслідок 3. Для того, щоб тільки менший корінь квадратного тричлена лежав між числами ![]()
для ![]()
![]()
![]()
![]()
які можна записати також у вигляді однієї системи ![]()
Наслідок 4. Для того, щоб один з коренів квадратного тричлена був меншим за ![]()
![]()
для ![]()
![]()
![]()
![]()
які можна записати також у вигляді однієї системи ![]()
Приклад 1. Знайти всі значення ![]()
![]() .
.
Розв’язання. Якщо ![]()
Отже, ![]()
![]()
Для того, щоб рівняння мало додатні корені, мають виконуватись умови:
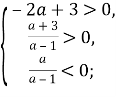
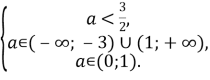
Система несумісна, отже, ні для яких значень ![]()
Відповідь: таких значень ![]()
Приклад 2.
Для яких значень ![]()
![]() має два від’ємні корені?
має два від’ємні корені?
Розв’язання. З умови задачі випливає, що ![]()
![]()
Для того, щоб рівняння мало від’ємні корені, необхідно, щоб виконувалася умова: 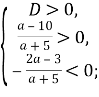
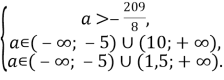
Отже, ![]() .
.
Відповідь: ![]() .
.
Приклад 3. Для яких значень параметра ![]()
![]()
![]()
Розв’язання. Оскільки старший коефіцієнт рівняння дорівнює одиниці, то для того, щоб число ![]()
![]()
![]()
Відповідь: ![]()
Приклад 4. Для яких значень ![]()
![]()
більші за 1?
Розв’язання. Старший коефіцієнт рівняння додатний, тому для того, щоб корені рівняння були більші за 1, треба, щоб виконувалися умови: 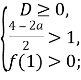
![]()
![]()
![]()
![]()
![]()
Враховуючи, що ![]() , дістанемо систему
, дістанемо систему 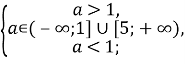 яка несумісна.
яка несумісна.
Відповідь: таких значень ![]()
Приклад 5.
Для яких значень параметра ![]()
![]() належать інтервалу (
належать інтервалу (![]()
Розв’язання. Старший коефіцієнт рівняння додатний, тому для того, щоб корені рівняння належали інтервалу (![]()
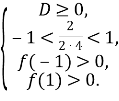
![]()
![]()
![]()
Умова ![]() виконується.
виконується.
Тоді маємо: 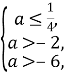 звідки
звідки ![]()
Відповідь: ![]() .
.
Рекомендовані вправи для розв’язання в класі і для домашнього завдання.
1. Знайти всі значення параметра ![]()
![]() .
.
2. При яких значеннях параметра ![]()
![]() ?
?
3. Знайти всі значення параметра ![]()
![]() більші за 3.
більші за 3.
4. Для яких дійсних значень параметра ![]()
![]() має один корінь, який більший за 3, а другий – менший за 2?
має один корінь, який більший за 3, а другий – менший за 2?
5. Знайти всі дійсні значення ![]()
![]() містяться між числами 0 і
містяться між числами 0 і ![]()
Відповіді: 1. ![]() 2.
2. ![]() 3.
3. ![]() 4.
4. ![]()
5. ![]()
ЗАЛІКОВА РОБОТА №1
Варіант 1.
1. При якому ![]()
![]() має корінь, рівний 5.
має корінь, рівний 5.
2. При якому ![]()
![]() не має розв’язків?
не має розв’язків?
3. Для кожного значення параметра розв’язати рівняння:
а) ![]() ;
;
б) ![]()
4. При якому ![]()
![]() має безліч розв’язків?
має безліч розв’язків?
5. При яких значеннях параметра а рівняння ![]() має єдиний корінь?
має єдиний корінь?
Варіант 2.
1. При якому ![]()
![]() має корінь, рівний 4.
має корінь, рівний 4.
2. При якому ![]()
![]() має безліч розв’язків?
має безліч розв’язків?
3. Для кожного значення параметра розв’язати рівняння:
а) ![]() ;
;
б) ![]()
4. При якому ![]()
![]() не має розв’язків?
не має розв’язків?
5. При яких значеннях параметра а рівняння ![]() має єдиний корінь?
має єдиний корінь?
ЗАЛІКОВА РОБОТА №2
Варіант 1.
1. При яких значеннях параметра ![]()
![]()
![]() ?
?
2. Розв’язати рівняння: 1) ![]() ;
;
2) ![]()
3) ![]()
3. Знайти всі значення параметра ![]()
![]()
![]() .
.
Варіант 2.
1. При яких значеннях параметра ![]()
![]() ?
?
2. Розв’язати рівняння: 1) ![]() ;
;
2) ![]()
3) ![]()
3. Знайти всі значення параметра ![]()
![]() .
.
Відповіді: Залікова робота №1.
Варіант 1. 1. ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,
якщо ![]()
Варіант 2. 1. ![]() 2.
2. ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Залікова робота №2.
Варіант 1. 1. ![]()
![]()
![]() 2) якщо
2) якщо ![]()
![]() 3) якщо
3) якщо ![]()
![]()
![]()
Варіант 2. 1. ![]() ; 2. 1) якщо
; 2. 1) якщо ![]()
![]()
![]() 3) якщо
3) якщо ![]()
![]()
![]()
СПИСОК ВИКОРИСТАНОЇ ЛІТЕРАТУРИ
1. А. В. Крамаренко. Розв’язання рівнянь та нерівностей з параметрами/
А. В. Крамаренко//Математика. – 2004. – №17-18. – с. 13-20.
2. А. Г. Мерзляк. Алгебра: підручник для 8 кл. з поглибл. вивченням математики/ Мезляк А. Г., Полонський В. Б., Якір М. С. – Х.: Гімназія, 2012. – 368 с.
3. А. Г. Мерзляк. Збірник задач і завдань для тематичного оцінювання з алгебри для 8 класу/ Мезляк А. Г., Полонський В. Б., Рабінович Ю. М., Якір М. С. – Х.: Гімназія, 2007. – 112 с.
4. В. Н. Литвиненко. Практикум по элементарной математике: алгебра, тригонометрия/ Литвиненко В. Н., Мордкович А. Г. – М.: Просвещение, 1991. – 352 с.
5. Е. А. Рубан. Розв’язування рівнянь, систем рівнянь та нерівностей з параметрами/ Е. А. Рубан// Математика. – 2003. – С. 6-24.
6. Збірник програм з математики для до профільної підготовки та профільного навчання (у двох частинах). Ч. І. Допрофільна підготовка/ Упоряд. Н. С. Прокопенко, О. П. Вакуленко, О. В. Єргіна. – Х.: Вид-во «Ранок», 2011. – 320 с.
7. Л. О. Щоголєва. Рівняння та системи рівнянь з параметрами/Л. О. Щоголєва, Г. С. Маслай. – Луцьк, 1999. – 28 с.
8. О. Г. Гайштут. Розв’язування алгебраїчних задач/ О. Г. Гайштут, Г. М. Литвиненко. – К.: Рад. шк., 1991. – 224 с.
9. О. Кравчук. Рівняння з параметрами/ О. Кравчук// Математика. – 2006. –- №13. – С. 17-24.
10. С. В. Сержук. Рівняння з параметрами/С. В. Сержук// Математика. – 2004. – №17-18. – С. 8-12.
1


про публікацію авторської розробки
Додати розробку
