Конспект "Формула Ньютона – Лейбніца"

Клас: 11

Предмет: Алгебра і початки аналізу

Тема уроку: Формула Ньютона – Лейбніца

Мета:

• навчальна:

ознайомити учнів з формулою Ньютона—Лейбніца та основними властивостями визначеного інтеграла, які випливають із власти­востей первісної і формули Ньютона—Лейбніца; формувати вміння застосовувати дану формулу для обчислення визначених інтегралів;  удосконалити вміння знаходити первісні для функцій;

• розвивальна:

розвити логічне мислення, пам'ять, увагу, спостережливість, вміння аналізувати, порівнювати, робити висновки; сприяти розвитку грамотної усної і письмової математичної мови;

• виховна:

виховати  взаємоповагу в колективі, чуйне ставлення один до одного, вміння розуміти точку зору співрозмовника, визнавати право на іншу думку; прищепити інтерес до предмету.

Тип уроку: засвоєння нових знань

Хід уроку

1. Організаційний момент.

Привітання. Організація класу до уроку.

2. Мотивація навчальної діяльності.

На минулому занятті ми познайомились з поняттям визначеного інтеграла та з його геометричним змістом. Безпосередньо за означенням визначені інтеграли легко обчислювати лише для найпростіших функцій. Однак, для інших функцій, наприклад тригонометричних, обчислення границь інтегральних сум значно ускладнюється. До того ж такий спосіб потребує важких і громіздких обчислень. Сьогодні ми познайомимось з іншим способом обчислення визначених інтегралів значно простішим та легшим. Тому після вивчення сьогоднішньої теми ви зможете обчислювати визначені інтеграли та познайомитесь з його властивостями. Щоб дізнатися тему сьогоднішнього заняття, вам необхідно пригадати деякий теоретичний матеріал,  розгадати кросворд та знайти ключове слово.

3. Актуалізація опорних знань учнів.

         « Фронтальне опитування»

За посиланням ми знайдемо завдання http://surl.li/jsmjf

(Нижче подані оригінал та відповіді до кросворду)

4. Вивчення нового матеріалу

Отже, ви відшукали ключове слово теми сьогоднішнього уроку і це – «формула». Авторами формули, яка дає другий спосіб обчислення визначених інтегралів, стали два визначних вчених – англійський фізик, математик, механік і астроном Ісаак Ньютон і німецький філософ, логік, математик, фізик, історик Готфрід Вільгельм Лейбніц. Отже, тема сьогоднішнього уроку – «Формула Ньютона – Лейбніца. Основні властивості визначеного інтеграла».

 (Доповідь учнів про життєвий шлях та наукову діяльність І. Ньютона і В. Лейбніца)

Формула Ньтона – Лейбніца

Якщо  функція f(x) визначена та  неперервна на відрізку [а; b] і F(x) — будь-яка первісна для функції f(x) на відрізку [а; b], то

.

 - скорочений запис різниці F(b) - F(a).

Формула Ньютона-Лейбніца  пов'язує поняття інтеграла й первісної для даної функції, і є правилом обчислення інтегралів.

Приклад 1. Обчисліть

Розв'язання:  Оскільки для функції f (x) = х² однією із первісних є F(x) =, то заданий інтеграл обчислюється безпосереднім застосуванням формули Ньютона – Лейбніца:

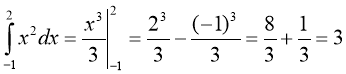          .                     Відповідь: 3.

Приклад 2. Обчисліть

Розв'язання:  Так як  для функції f (x) = 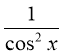  однією із первісних є F(x) =, то маємо: .                 Відповідь: 1.

Із властивостей первісної і формули Ньютона-Лейбніца ви­пливають основні властивості інтеграла: 

1.     .

Доведення:

2.     .

Доведення:

3.     Постійний множник можна виносити за знак інтеграла:

Доведення: Якщо F(х) є первісною для функції f(x), то для функції kf(x) первісною буде функція kF(х). Тоді

4.     Інтеграл суми (різниці) функцій дорівнює сумі (різниці) інтегралів :

.

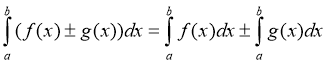Доведення: Доведемо цю властивість для інтеграла суми функцій. Нехай F(х) – первісна для функції f(x), а G(х) – первісна для функції g(х), то для функції  f(x) + g(х) первісною буде функція F(х) + G(х). Тоді

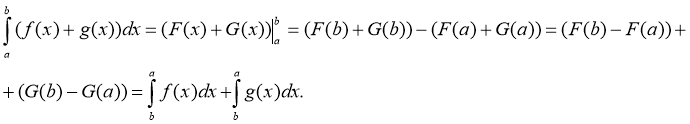Аналогічно доводиться інтеграл різниці функцій.

5.     Якщо функція f (x) інтегрована на [а; b] і с [а; b], то

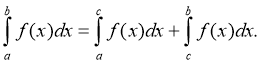
Доведення: Нехай F(x) — первісна для функції f(x). Тоді

Додаючи почленно ліві і праві частини рівностей, одержуємо:

Приклад 3. Обчисліть .

Розв'язання: Використовуючи  властивості визначеного інтеграла (властивість 4), запишемо даний інтеграл як різницю двох інтегралів, кожний з яких безпосередньо можна обчислити за формулою Ньютона – Лейбніца:  

.

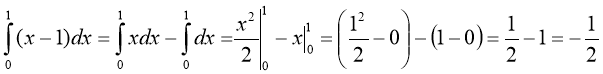Відповідь: .

5. Закріплення вивченого матеріалу.

Завдання. Обчистити інтеграли  (колективне розв’язання вправ)

Розв'язання: Відповідь: 

2)  

Розв'язання:

Відповідь: 

3)

Розв'язання:

 .

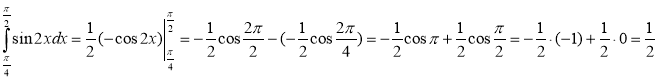6. Самостійна робота.

Перейдіть за посиланням та виконайте завдання самостійної роботи http://surl.li/jsljg

Розв’язання та відповіді до самостійної роботи

7. Підсумок уроку.

Запитання до класу:

1. Запишіть формулу Ньютона-Лейбніца
2. Сформулюйте властивості визначених інтегралів

8. Домашнє завдання. 

Опрацювати: параграф 11 підручника О. Істер «Математика» http://surl.li/akxqc

Розв’язати № 11.3 № 11.5 №11.7 (2, 3) 

Додаток

Питання до кросворду:

1. Як називається операція знаходження похідних?  (Диференціювання)
2. З якою величиною фігури пов'язаний геометричний зміст визначеного інтеграла. (Площа)
3. Як називається функція F(х) для функції f (х) на деякому проміжку, якщо для будь-якого х із цього проміжку F' (х) = f (х).  (Первісна)
4. Як називаються числа а і b в позначені визначеного інтеграла.  (Межа)
5. Як називається операція, обернена до диференціювання. (Інтегрування)
6. Як називається сукупність усіх первісних для даної функції f (х). (Інтеграл)
7. Як називається фігура, обмежена графіком неперервної і невід'ємної на відрізку [а; b]  функції у = f(x), відрізком [а; b] осі Ох і прямими x = а, х = b. (Криволінійна трапеція)