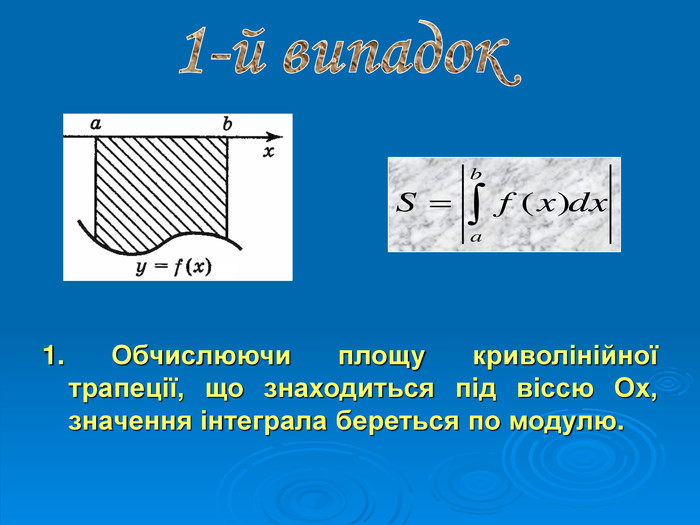
Конспект та презентації для уроку алгебри у 11 класу на тему: "Застосування інтеграла для обчислення площ фігур"
Варіант – 1
№ 2.
а) 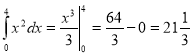 .
.
б) 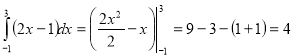 .
.
в) 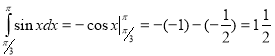 .
.
№ 5.
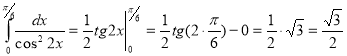 .
.
Варіант – 2
№ 2.
а) 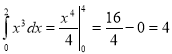 .
.
б) 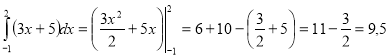 .
.
в) 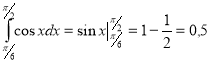 .
.
№ 5.
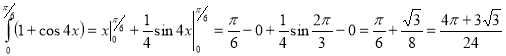
№ 1.
Обчислити площу фігури, обмеженої лініями ![]() ,
, ![]() при
при ![]() .
.
№ 2.
Обчислити площу фігури, обмеженої лініями ![]() ,
, ![]() .
.
№ 3.
Річка тече лугом і двічі перетинає перетинає шосе, утворюючи криву ![]() . Яка площа лугу між шосе та річкою (у км2), якщо вважати, що лінія шосе збігається з віссю Ох. Одиниця довжини – 1 км. (Завдання із ЗНО-2010)
. Яка площа лугу між шосе та річкою (у км2), якщо вважати, що лінія шосе збігається з віссю Ох. Одиниця довжини – 1 км. (Завдання із ЗНО-2010)
№ 4.
Обчислити площу фігури, обмеженої лініями ![]() ,
, ![]() при
при ![]() .
.
№ 1.
Обчислити площу фігури, обмеженої лініями ![]() ,
, ![]() при
при ![]() .
.
№ 2.
Обчислити площу фігури, обмеженої лініями ![]() ,
, ![]() .
.
№ 3.
Річка тече лугом і двічі перетинає перетинає шосе, утворюючи криву ![]() . Яка площа лугу між шосе та річкою (у км2), якщо вважати, що лінія шосе збігається з віссю Ох. Одиниця довжини – 1 км. (Завдання із ЗНО-2010)
. Яка площа лугу між шосе та річкою (у км2), якщо вважати, що лінія шосе збігається з віссю Ох. Одиниця довжини – 1 км. (Завдання із ЗНО-2010)
№ 4.
Обчислити площу фігури, обмеженої лініями ![]() ,
, ![]() при
при ![]() .
.
№ 1.
Обчислити площу фігури, обмеженої лініями ![]() ,
, ![]() при
при ![]() .
.
№ 2.
Обчислити площу фігури, обмеженої лініями ![]() ,
, ![]() .
.
№ 3.
Річка тече лугом і двічі перетинає перетинає шосе, утворюючи криву ![]() . Яка площа лугу між шосе та річкою (у км2), якщо вважати, що лінія шосе збігається з віссю Ох. Одиниця довжини – 1 км. (Завдання із ЗНО-2010)
. Яка площа лугу між шосе та річкою (у км2), якщо вважати, що лінія шосе збігається з віссю Ох. Одиниця довжини – 1 км. (Завдання із ЗНО-2010)
№ 4.
Обчислити площу фігури, обмеженої лініями ![]() ,
, ![]() при
при ![]() .
.
№ 1.
Обчислити площу фігури, обмеженої лініями ![]() ,
, ![]() при
при ![]() .
.
№ 2.
Обчислити площу фігури, обмеженої лініями ![]() ,
, ![]() .
.
№ 3.
Річка тече лугом і двічі перетинає перетинає шосе, утворюючи криву ![]() . Яка площа лугу між шосе та річкою (у км2), якщо вважати, що лінія шосе збігається з віссю Ох. Одиниця довжини – 1 км. (Завдання із ЗНО-2010)
. Яка площа лугу між шосе та річкою (у км2), якщо вважати, що лінія шосе збігається з віссю Ох. Одиниця довжини – 1 км. (Завдання із ЗНО-2010)
№ 4.
Обчислити площу фігури, обмеженої лініями ![]() ,
, ![]() при
при ![]() .
.
Графічний кросворд
|
1 |
|
|
|
|
|
|
|||||||
|
|
2 |
|
|
|
|
|
|
|
|
||||
|
3 |
|
|
|
|
|
||||||||
|
4 |
|
|
|
|
|
|
|
|
|||||
|
5 |
|
|
|
|
|
|
|
|
|||||
|
6 |
|
|
|
|
|
||||||||
|
7 |
|
|
|
|
|
|
|
||||||
|
8 |
|
|
|
||||||||||
Запитання
- Вчений ім’ям якого названа формула для обчислення визначеного інтеграла.
-
Графік функції
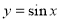 .
.
- Вчений ім’ям якого названа формула для обчислення визначеного інтеграла.
- Функція, що застосовується для знаходження визначеного інтеграла.
-
Графік функції
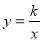 .
.
-
Графік функції
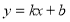 .
.
-
Графік функції
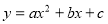 .
.
-
Графік рівняння
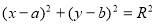 .
.













Тема. Застосування інтеграла для обчислення площ фігур.
Мета: розглянути деякі види плоских фігур площу яких вдається обчислити за допомогою визначеного інтеграла; формувати вміння застосовувати інтеграл до обчислення площ фігур; показати можливість застосування ПЗ «Master Function 2.0» до знаходження визначеного інтеграла, побудови графіків функцій, розв’язування квадратних рівнянь; формувати навички порівняння розв’язків, отриманих аналітичним і програмними способами; виховувати культуру математичних записів, обчислювальних навичок; розвивати інтерес до навчання та навички роботи з комп’ютером.
Обладнання: математичні таблиці, комп’ютер, мультимедійний проектор, ПЗ «Master Function 2.0», комп’ютерні презентації «Уний рахунок», «Випадки обчислення площ деяких фігур за допомогою інтеграла», «Приклади розв’язання» завдань.
Тип уроку: формування вмінь і навичок учнів, інтегрований урок.
Очікувані результати: Після уроку учні зможуть:
- розрізняти випадки деяких фігур, площі яких можна обчислити за допомого інтеграла;
- удосконалити свої вміння обчислювати визначені інтеграли та площі фігур;
- користуватися інтерфейсом ПЗ «Master Function 2.0» та практично знаходити визначені інтеграли, будувати графіки функцій.
Хід уроку
1. Організаційний момент.
2. Усний рахунок.
Алгебра, яку ми вивчаємо в 11 класі, займається функціональним аналізом, а саме зараз ми вивчаємо інтегральне числення. Та все ж не забуваймо, що вона є наступницею арифметики. Тому давайте наш урок розпочнемо із невеличкої обчислювальної розминки.
3. Перевірка домашнього завдання.
На домашнє завдання учням було задано № 2, 5 (В-1, В-2) із карток-завдань.
Перевірку домашнього завдання учні здійснюють за допомогою наперед заготовлених розв’язків у вигляді комп’ютерної презентації.
4. Актуалізація опорних знань.
(Запитання до класу на основі презентації кросворду).
Запитання графічного кросворду
- Вчений ім’ям якого названа формула для обчислення визначеного інтеграла.
-
Графік функції
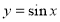 .
.
- Вчений ім’ям якого названа формула для обчислення визначеного інтеграла.
- Функція, що застосовується для знаходження визначеного інтеграла.
-
Графік функції
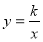 .
.
-
Графік функції
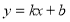 .
.
-
Графік функції
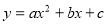 .
.
-
Графік рівняння
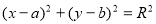 .
.
|
1 |
|
|
|
|
|
|
|||||||
|
|
2 |
|
|
|
|
|
|
|
|
||||
|
3 |
|
|
|
|
|
||||||||
|
4 |
|
|
|
|
|
|
|
|
|||||
|
5 |
|
|
|
|
|
|
|
|
|||||
|
6 |
|
|
|
|
|
||||||||
|
7 |
|
|
|
|
|
|
|
||||||
|
8 |
|
|
|
||||||||||
5. Повідомлення теми, мети і завдань уроку. Мотивація навчальної діяльності.
(Цей етап уроку здійснюється за допомогою комп’ютерної презентації.)
6. Формування вмінь і навичок обчислення площ плоских фігур.
(Клас об’єднано у 2 групи по 5 чи 6 учнів. Умовно назвемо їх аналітиками(учні, які розв’язують завдання за допомогою математичних алгоритмів) та практиками(розв’язують завдання за допомогою комп’ютера).
Розглядаються різні види плоских фігур, площі яких вдається обчислити за допомогою інтеграла.
(пояснення на основі комп’ютерної презентації)
 Учитель математики.
Учитель математики.
Ще раз згадаємо, що за геометричним змістом інтеграла, його значення чисельно дорівнює площі криволінійної трапеції, обмеженої графіком функції ![]() на відрізку
на відрізку ![]() .
.
Розглянемо приклад № 5 із підручника (стр. 136):
Приклад 5. Обчислити площу фігури, обмеженої синусоїдою ![]() і відрізком
і відрізком ![]() осі Ох.
осі Ох.
Розв’язання.
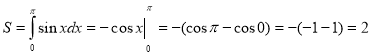 (кв. од.).
(кв. од.).
Відповідь: 2.
Учитель інформатики.
Показує як за допомогою ПЗ «Master Function 2.0» можна швидко виконати це ж завдання.
Учитель математики.
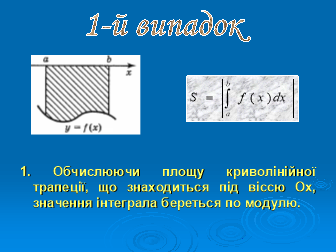 Випадок 1. Обчислюючи площу криволінійної трапеції, що знаходиться під вісь Ох отримаємо від’ємне значення інтеграла, тому
Випадок 1. Обчислюючи площу криволінійної трапеції, що знаходиться під вісь Ох отримаємо від’ємне значення інтеграла, тому 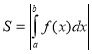 .
.
Приклад. Обчислити площу фігури, обмеженої графіком функції ![]() та прямими
та прямими ![]() та віссю Ох.
та віссю Ох.
Розв’язання.
Графік показати за допомогою ПЗ «Master Function 2.0».
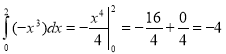 ,
, ![]() (кв. од.).
(кв. од.).
Відповідь: 4.
Переконатися в правильності обчислень на комп’ютері.
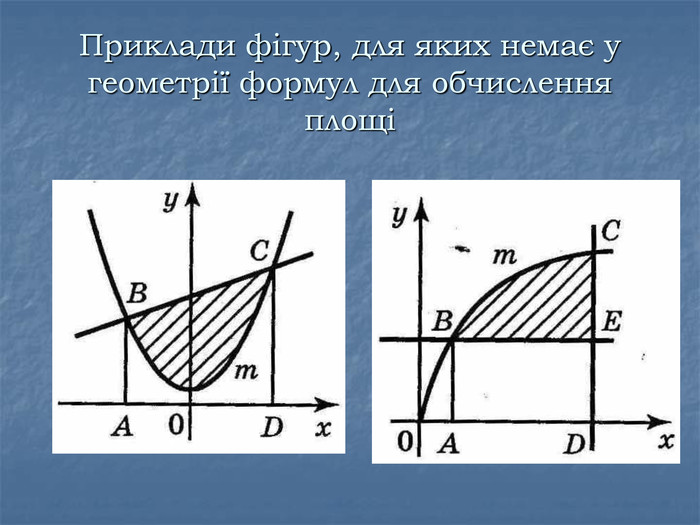
Випадок 2.  Площу фігури, обмеженої графіками двох функцій (зверху та знизу) та прямими
Площу фігури, обмеженої графіками двох функцій (зверху та знизу) та прямими ![]() , можна обчислити як різницю площ двох криволінійних трапецій:
, можна обчислити як різницю площ двох криволінійних трапецій: 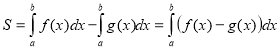
Легко обґрунтувати, що цю ж формулу можна застосовувати, якщо фігура, площу якої треба обчислити, повністю або частково знаходиться під віссю Ох.
Приклад. Обчислити площу фігури, обмеженої графіками функцій![]() та
та ![]() .
.
Розв’язання.
Графіки показати за допомогою ПЗ «Master Function 2.0». Бачимо що абсциси точок перетину графіків цих функцій ![]() . Тому:
. Тому:
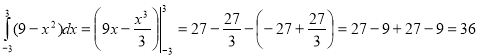 (кв. од.).
(кв. од.).
Відповідь: 36.
Один з учнів-практиків перевіряє отриманий результат на комп’ютері.
Обдумаємо ще дві ситуації, коли площу фігури вдається обчислити як суму чи різницю двох криволінійних трапецій.
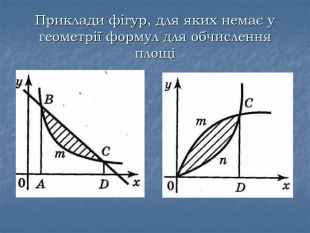
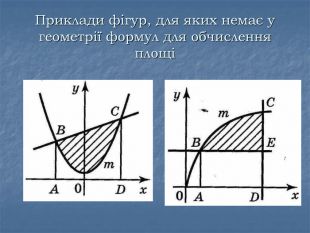
Випадок 3. 
Випадок 4.

7. Гумористична пауза.
8. Розв’язування вправ.
А зараз розглянемо приклади знаходження площ плоских фігур.
№ 1.
Обчислити площу фігури, обмеженої лініями ![]() ,
, ![]() при
при ![]() .
.
Розв’язання.
Побудуємо схематично фігуру площу, якої треба обчислити. Отримуємо криволінійну трапецію, що знаходиться під віссю Ох. Тому:
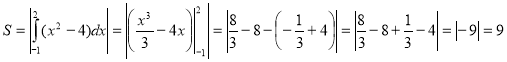 (кв. од.).
(кв. од.).
Відповідь: 9.
Один з учнів-практиків перевіряє отриманий результат на комп’ютері.
№ 2.
Обчислити площу фігури, обмеженої лініями ![]() ,
, ![]() .
.
Розв’язання.
Побудуємо схематично фігуру площу, якої треба обчислити. Отримуємо фігуру, обмежену зверху прямою, а знизу параболою. Межі інтегрування є абсцисами точок перетину графіків цих функцій. Для їх знаходження розв’яжемо систему цих рівнянь 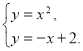 Тобто
Тобто ![]() . На цьому етапі знову скористаємося допомогою ПЗ «Master Function 2.0» і отримаємо
. На цьому етапі знову скористаємося допомогою ПЗ «Master Function 2.0» і отримаємо ![]() . Тоді
. Тоді
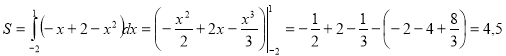 (кв. од.).
(кв. од.).
Відповідь: 4,5.
Один з учнів-практиків перевіряє отриманий результат на комп’ютері.
№ 3.
Річка тече лугом і двічі перетинає перетинає шосе, утворюючи криву ![]() . Яка площа лугу між шосе та річкою (у км2), якщо вважати, що лінія шосе збігається з віссю Ох. Одиниця довжини – 1 км. (Завдання із ЗНО-2010)
. Яка площа лугу між шосе та річкою (у км2), якщо вважати, що лінія шосе збігається з віссю Ох. Одиниця довжини – 1 км. (Завдання із ЗНО-2010)
Розв’язання.
Перетин річки та шосе – це точки перетину графіка функції з віссю Ох. Для їх знаходження розв’яжемо рівняння ![]() .
. ![]() . Тоді
. Тоді
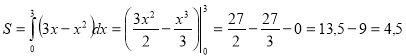 (кв. од.).
(кв. од.).
Відповідь: 4,5.
Один з учнів-практиків перевіряє отриманий результат на комп’ютері.
Проблемна ситуація.
А зараз кожна з груп отримає одне і теж завдання на обчислення площі фігури. Аналітики розв’яжуть його аналітичним способом, а практики – за допомогою комп’ютера. А потім перевіримо чи співпадають отримані результати.
№ 4.
Обчислити площу фігури, обмеженої лініями ![]() ,
, ![]() при
при ![]() .
.
Розв’язання.
Побудуємо схематично фігуру площу, якої треба обчислити. Отримуємо криволінійну трапецію, що знаходиться над віссю Ох. Тому:
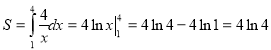 (кв. од.).
(кв. од.).
Практики отримують приблизний результат 5,545192. Цього разу відповіді не співпадають. Як визначити хто з вас правильно розв’язав завдання?
Учні пробують пояснити цю ситуацію.
Відповідь: ![]() .
.
Додаткові завдання.
№ 5.
Обчислити площу фігури, обмеженої параболами ![]() і
і ![]() та віссю Ох.
та віссю Ох.
Розв’язання.
Побудуємо схематично фігуру площу, якої треба обчислити. Межі інтегрування є абсцисами точок перетину графіків цих функцій. Для їх знаходження розв’яжемо систему цих рівнянь 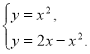 Тобто
Тобто ![]() .
. ![]() . Тоді
. Тоді
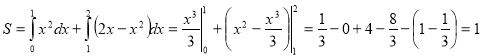 (кв. од.).
(кв. од.).
Відповідь: 1.
Один з учнів-практиків перевіряє отриманий результат на комп’ютері.
7. Підведення підсумків уроку.
Усний тест із ЗНО-2010.(на зображенні)
Ще раз нагадати види фігур, площі яких вдається обчислити за допомогою інтеграла.
Також наголосити на перевагах та недоліках аналітичного та практичного методів розв’язування завдань такого типу.
8. Домашнє завдання.
§ 26, запитання 1 – 3
№ 64(2) – 1-й і 2-й рівні;
№ 64(8) – 3-й і 4-й рівні;
1

про публікацію авторської розробки
Додати розробку












![Площа криволінійної трапеції, обмеженої графіком функції у=f(x), дорівнює інтегралу від цієї функції на відрізку [a; b]. Площа криволінійної трапеції, обмеженої графіком функції у=f(x), дорівнює інтегралу від цієї функції на відрізку [a; b].](/uploads/files/13863/222665/238521_images/1.jpg)