Конспект уроку"Арифметична і геометрична прогресії. Розв’язування прикладних задач»

Про матеріал

Тема уроку: «Арифметична і геометрична прогресії. Розв’язування прикладних задач» Мета уроку: навчальна: поглибити знання учнів про арифметичну і геометричну прогресії, навчити застосовувати знання про прогресії для розв’язування життєвих задач, задач, пов’язаних з розмноженням, з рухом тіл в просторі;

Перегляд файлу

«Арифметична і геометрична прогресії. Розв’язування прикладних задач»

Мета уроку:

навчальна: поглибити знання учнів про арифметичну і геометричну прогресії, навчити застосовувати знання про прогресії для розв’язування життєвих задач, задач, пов’язаних з розмноженням, з рухом тіл в просторі;

розвиваюча: розвивати уявлення про ідеї і методи математики та їх роль в розв’язанні біологічних, фізичних задач;

виховна: виховувати культуру записів, любов до поезії.

Епіграф уроку: . «Якщо говорити про математику, то її досягнення дедалі ширше застосовуються в найрізноманітніших галузях науки, техніки, економіки»

Ю.О. Митропольський

Вислови:

«Немає жодної галузі математики, якою б абстрактною вона не була, котра

коли-небудь не виявиться застосовною до явищ дійсного світу»

М.І.Лобачевський

“Дорогі не ті знання, які відкладаються в мозку, як жир, а дорогі ті, які перетворюються в розумові м’язи”

“Вміння розв’язувати задачі – практичне мистецтво, подібне плаванню або катанню на лижах, або грі на фортепіано; навчитися цьому можна лише ,уподібнюючись вибраним зразкам і постійно тренуючись”

Д.Пойа

Тип уроку: застосування знань, умінь і навичок.

Обладнання: комп’ютер, проектор, екран.

Форми і методи роботи: ігрові методи, колективні форми роботи, індивідуальна самостійна робота учнів.

Хід уроку

І. Перевірка домашнього завдання.

Задача №1

Сьогодні ми з вами проводимо другий урок з теми «Арифметична і геометрична прогресії. Розв’язування прикладних задач». Запишіть тему уроку.

Епіграф уроку: . «Якщо говорити про математику, то її досягнення дедалі ширше застосовуються в найрізноманітніших галузях науки, техніки, економіки»

Ю.О. Митропольський

Прогресії є відображенням світу, що нас оточує. На попередньому уроці ми розглянули задачі з даної теми з далекої давнини. На сьогоднішньому задачі, пов’язанні із сучасним життям.

ІІ. Мотивація навчальної діяльності

Почати урок хочу з історії, яка сталася давно.

Одного разу незнайомець постукав у вікно до багатого купця і запропонував таку угоду: «Я буду кожного дня протягом 30 днів приносити тобі по 100 000 крб. А ти мені першого дня за 100 000 крб. даси 1 к., другого дня за 100 000 крб. – 2 к. і так кожного дня будеш збільшувати винагороду в 2 рази. Якщо ти зацікавився цією угодою, то з завтрашнього дня і почнемо.» Купець зрадів такій нагоді розбагатіти. Він підрахував, що за 30 днів отримає від незнайомця 3 000 000 крб. Наступного дня пішли до нотаріуса і підписали угоду. Хто залишиться у виграші?

Купець одержить 3 000 000крб.; незнайомець одержить 10 737 418,24крб. Програв купець.

Такі несподівані результати бувають і в наші дні, коли не знаєш і не хочеш вчити математики.

Найціннішим у вивченні предмету є використання набутих знань у життєвих ситуаціях.

Тож, на сьогоднішньому уроці ми маємо поглибити знання про арифметичну і геометричну прогресії, навчитися застосовувати знання про прогресії для розв’язування життєвих задач, задач, пов’язаних з її застосуванням під час вивчення питань інших наук і життєвих ситуацій.

То ж ми вирушимо на віртуальному поїзді, щоб знайти, де застосовуються прогресії у реальному житті, щоб дати відповідь на запитання:

Перш, ніж вирушити у ПОДОРОЖ, перевіримо чи маємо необхідний багаж: теоретичний матеріал та вміння його застосовувати.

ІV. Актуалізація опорних знань

1.«Математичне лото»

Назва формули	Буквений запис
Рекурентна формула арифметичної прогресії
Рекурентна формула геометричної прогресії
Різниця арифметичної прогресії
Знаменник геометричної прогресії
Формула п-го члена арифметичної прогресії
Формула п-го члена геометричної прогресії
Властивість членів арифметичної прогресії
Властивість членів геометричної прогресії
Сума п- членів арифметичної прогресії
Сума п- членів геометричної прогресії

«Немає жодної галузі математики, якою б абстрактною вона не була, котра коли-небудь не виявиться застосовною до явищ дійсного світу» М.І.Лобачевський

“Дорогі не ті знання, які відкладаються в мозку, як жир, а дорогі ті, які перетворюються в розумові м’язи” Герберт Спенсер

2.«Математична естафета»

№1. Усі написані послідовності – арифметичні прогресії. Чи так це? Вкажіть номер неправильної відповіді, якщо вона є.

1) 5; 7; 9; 11; …

2) 20; 10; 0; -10; …

3) 2; 4; 6; 8; …

4) 1; 2; 6; 8; …

5) 15; 3; -9; …

№2. Усі наступні послідовності – геометричні прогресії. Чи правильно це?

1) 2; 4; 8; 16; …

2) 200; 20; 2; …

3) 3; -6; 12; …

4) 1; 4; 16; …

5) 8; 4; 0; -4; …

№3 Знайдіть п'ятий член геометричної прогресії 200; 20; 2; …

№4 Знайдіть суму чотирьох перших членів арифметичної прогресії 10; 6; 2; ....

№5 Придумайте арифметичну прогресію, сума перших трьох членів якої дорівнює 60

Ну що ж, необхідний багаж з нами. То ж ми вирушаємо.

V. Розв'язування задач прикладного змісту

Наш потяг прибув на першу зупинку. Ми отримали перше завдання.

І зупинка

«Комунікаційна»

Тут новини дуже швидко поширюються.

Щоб можна вирушити далі нам потрібно розв'язати задачу, пов'язану з поширення чуток у селі, якому зупинились. Конверт під назвою

«ХТО ШВИДШЕ ОБЧИСЛЮЄ?»

Задача 1. Поширення чуток. До села з 3000-тисячним населенням о 8-й годині ранку прибув мешканець столиці і привіз свіжу новину. У будинку, де зупинився, він повідомив новину лише трьом жителям. Це зайняло, 15 хв, тобто о 8.15 новина була відома чотирьом: приїжджому і трьом жителям. Довідавшись новину, кожний із трьох громадян розповів про неї трьом іншим. На це знадобилося теж 15 хв. Якщо чутка поширюватиметься з такою швидкістю, то скільки пройде часу, перш ніж усе село дізнається про неї?

1,3,9,27,81,243,729, 2187….

Бачимо, що в задачі поширення чуток відповідає геометричній прогресії. У житті тут все набагато складніше.

Рушаємо дальше.

ІІ зупинка

«Фізична» Повідомлення учнів про використання арифметичної і геометричної прогресії у фізиці.

2.Робота в групах

Задача для І групи

Задача №2. Тіло, яке вільно падає з Пізанської вежі, проходить за першу секунду 4,9 м, а за кожну наступну – на 9,8 м більше, ніж за попередню. Яку відстань проходить тіло за 4 секунду?

a1=4,9; d=9,8 a

a=a+d(n-1)

а=4,9+(4-1)9,8=34,3(м)

Задача№3. Гальмуючи, автомобіль за першу секунду проїхав 12м, а за кожну наступну

на 2м менше, ніж за попередню.

a₁=12, d=-2, a_n=0

a_n=a₁+d(n-1)

0=12-2(n-1)

n=7

S₇=42(м)

Відповідь: 42м - гальмівний шлях автомобіля.

ІІІ зупинка «Біологічна»

Колективна робота

Задача №4

19.12.• Бактерія, потрапляючи в сприятливе середовище, наприкінці

двадцятої хвилини ділиться на дві бактерії, кожна з яких на-

прикінці наступних 20 хв ділиться знову на дві й т. д. Скільки

бактерій утворюється з однієї бактерії протягом доби?

Розв’язування

b1 =1, b2 =2, b3 =4,…

Доба – 24 год, 24* 60 хв = 1440 хв

За добу пройде ділення 72 рази

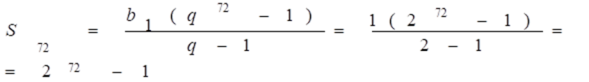
Відповідь:

ІV зупинка «Медична»

Самостійна робота

Задача №5. Кожний курець викурює в день у середньому 8 сигарет. Після викурювання першої сигарети в легенях осідає 0,0002 г. нікотину й тютюнового дьогтю. З кожною наступною сигаретою ця кількість збільшується на 0,000001 г. Яка кількість шкідливих речовин осідає в легенях за рік? (Відповідь: 4,846 г.).

8*365=2920(сигарет)

0,0002+0,0000001*(2920-1)=0,0003119(г)

х 2920=4,846(г)

V зупинка « Грошова»

«Хто перший»(Учень біля дошки)

Задача №6

Молодий чоловік отримав спадщину. За перший місяць він витратив 1000$, а кожний наступний місяць він витрачав на 500$ більше , ніж за попередній. Скільки доларів він витратив за другий місяць? За третій?, Який розмір спадщини, якщо грошей вистачило на рік такого безбідного життя?

а=1000; d=500; S-?

Використовуємо формулу а= а+ d(n-1).

а=1000+500(12-1)=6500($).

Використовуємо формулу

S=х n S=х12=45000($)

VІ зупинка «Практична»

Задача №7

Селянин продавав коня за 20000 грн. Але покупець, подумавши , відмовився, вважаючи, що це дорого. Тоді селянин запропонував таку умову: «Купи в мене тільки цвяхи для підков, яких у кожній підкові 6, а коня дістанеш на додачу. За перший дай к., за другий - к., за третій – 1 к. і т. д.». Щоб ви порадили покупцеві?

Розв'язання

Числа , 1,…., в - члени геометричної прогресії, де в=, g=2, n=24 (є цвяхи в усіх підковах). Тоді сума грошей, що треба заплатити за ці цвяхи, дорівнює

S=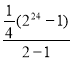= ≈4194303,7(к.) ≈41943(грн.)

Отже, вартість цвяхів становить наближено 41943 грн, що значно більше за 20000 грн.

Відповідь: на таку пропозицію не потрібно погоджуватися.

VІІ зупинка «Зв'язкова»

Оператор мобільного звя'зку запропонував акцію на наступних умовах: плата за з'єднання відсутня; за першу хвилину абонент платить 60к. , а за кожну наступну хвилину – на 5к. менше, ніж за попередню. Плата за тринадцяту і всі наступні хвилини не нараховується. Умови виконуються для здійснення дзвінків всіх мобільних операторів країни.

Скільки буде коштувати абоненту п'ята хвилина розмови?
Скільки буде коштувати абоненту розмова протягом п'яти хвилин?
Запишіть формулу, за допомогою якої можна обчислити вартість к-ї хвилини розмови.
Запишіть формулу, за допомогою якої можна обчтслити вартість розмови в n хвилин.

VII. Підсумок уроку

Наш потяг завершив свій маршрут.

Ян Амос Коменський говорив: «Уважай нещасним той день або ту годину, у яку ти не засвоїв нічого нового, нічого не додав до свого розвитку». Я сподіваюсь, що на сьогоднішньому уроці ви знайшли для себе хоч крапельку корисного.

На сьогоднішньому уроці ви побачили, що розв’язуючи задачі з біології, фізики можна використати властивості і формули арифметичних та геометричних прогресій, що приведе, іноді, до єдиного вірного шляху розв’язування цих задач.

VIII. Домашнє завдання.

На ваших партах лежать завдання, які склали учні 9 – их класів. Звертаю увагу на те, що під час роботи над даними задачами ,потрібно не тільки вникати в математичну суть задачі, а й вдумуйтесь в її зміст, з’ясовуйте життєву проблематику того чи іншого завдання. Ці задачі ви розв’яжете вдома і визначте, яка задача найцікавіша.

1.Задачі, які склали учні

Задача 1

Швидкісний автомобіль при встановленні рекорду за перші 2с розігнався до швидкості 20км/год, кожні наступні 2с його швидкість збільшувалась у два рази. Знайти швидкість, яку буде мати автомобіль у кінці 14с.

Задача 2

В організм собаки потрапила одна бактерія. До кінця тридцятої хвилини вона розділилася на дві, кожна з них до кінця тридцятої хвилини знову ділиться на дві і т. д. Скільки бактерій буде в організмі собаки через 5 годин?

Задача 3

У минулому році бабуся посадила на городі дві цибулини тюльпанів. Восени, коли бабуся викопала тюльпани, з’ясувалося, що із кожної цибулини виросло три. Бабуся попросила порахувати:

Скільки тюльпанів виросте на п’ятий рік?
Скільки всього тюльпанів виросте на городі за п’ять років?

Задача 4

Продавались на базарі яблука по 1грн за кілограм. Покупцю це здалося занадто дорого. Тоді він запропонував 10коп за перший кілограм, а за кожний наступний

2.Скласти умову задачі по темі «Арифметична прогресія в житті й побуті» (на окремому аркуші) і розв'язати її.

Задача групи 4

Задача від альпіністів. Турист, піднімаючись на гору, за першу годину досягає висоти 800м, а його восьми кілограмовий рюкзак щогодини стає легшим на 1 кг. Яка подія настане швидше: спорожніє рюкзак чи турист підніметься на висоту 5700 м, якщо за кожну наступну годину він піднімається на висоту на 25 м меншу, ніж за попередню?

Кажуть, що у 1723 році український гетьман Павло Полуботок поклав до Банку Англії свої скарби. 80% капіталу заповідав незалежній Україні. В скільки разів збільшився його капітал до 2017 року?

Розв’язування

Нехай А карбованців - початковий капітал, який покладений під 4% річних.

Через 1 рік внесок склав 1,04 А карбованців, на 2 рік - 1,042 А карбованців,

через 3 роки – карбованців, …

Маємо геометричну прогресію, де b1 = А, q =1,04

Гроші гетьмана залишилися упродовж 294 роки недоторканими,

то b294 = карбованців

Внесок до теперішнього часу збільшився у 97897 разів

Якщо б ці гроші дісталися незалежній Україні, то як би наша країна збагатилася.

Зверніть увагу на те, що коли ви гроші покладете до банку та будете знімати відсотки щомісячно, то ваш капітал буде зростати у арифметичній прогресії. А якщо влад покладете на рік, то ваші доходи зросту Задача-жарт

«ХТО ШВИДШЕ ОБЧИСЛЮЄ?»

Задача 1. Поширення чуток. До міста з 50-тисячним населенням о 8-й годині ранку прибув мешканець столиці і привіз свіжу новину. У будинку, де зупинився, він повідомив новину лише трьом жителям. Це зайняло, 15 хв, тобто о 8.15 новина була відома чотирьом: приїжджому і трьом жителям. Довідавшись новину, кожний із трьох громадян розповів про неї трьом іншим. На це знадобилося теж 15 хв. Якщо чутка поширюватиметься з такою швидкістю, то скільки пройде часу, перш ніж усе місто дізнається про неї? ( 2 год 30 хв )

ть у геометричній прогресії.

Вчитель: В біології прогресії пов’язані з такими темами, як розмноження, поділ клітин, формені елементи крові та інші. Неможливо розв’язати біологічні задачі з даних тем, не використавши знання про прогресії. За теорією еволюції Дарвіна, всі процеси, які пов’язані з живими організмами, відбуваються прогресивно або регресивно.

На стадії ембріона відбувається процес формування тканин, який називається гістогенез. Одним з видів сполучної тканини, яка формується на стадії формування ембріона, є кров, до складу якої входять життєво необхідні клітини – еритроцити, лейкоцити та тромбоцити, кількість яких впливає на самопочуття людини.

Як впливає кількість еритроцитів на самопочуття людини?

Вашій увазі пропонується задача № 5 (Сдайд 12)

Задача № 5. Кількість еритроцитів ( з розрахунку на 1 мм³) в крові людини становить на рівні моря – 5 мільйонів. Через кожні 600 м підняття в гору їх кількість збільшується на 1 мільйон. Яка кількість еритроцитів буде в крові людини, якщо вона підніметься на вершину гори Еверест (4800 м) . Чому це відбувається?

Застосуйте ваші знання з математики.

Тема: "Послідовності".

Прогресії виражають закони деяких фізичних явищ: тіло, що вільно падає, рухається рівноприскорено: відрізки шляху, пройдених цим тілом за першу, другу, третю,…секунду становить арифметичну прогресію.

1. Кулька котиться у жолобі за першу секунду проходить 0,6м, а за кожну наступну на 0,6м більше. За скільки часу вона пройде 6м?

2. Два тіла, знаходячись на відстані 158м один віл одного почали рухатись одночасно назустріч один з одним. Перше тіло рухається зі швидкістю 10 м/с, а друге в першу секунду пройшло 3м, а в кожну наступну на 5м більше, ніж в попередню. Через скільки секунд тіла зустрінуться?

3. У горах температура повітря літом при підніманні на кожні 100м в середньому знижується на 0,7°С. Об 11год. на горі термометр показував 14,8˚С. На якій висоті знаходиться спостерігач, якщо у підніжжя в цей час температура 26°С?

4. Бригада механізаторів в перший день зорали 100га поля, а в кожний наступний - на 3га більше, ніж в попередній. Знайти скільки гектарів поля бригада зоре за 19 днів.

5. Залізний стрижень, довжина якого при 0˚С дорівнює 1м, змінює свою довжину по закону арифметичної прогресії з різницею 0,000012м при послідовних змінювань температури на 1С°. Знайти довжину стрижня при 100°С?

6. Робітник обслуговує 16 верстатів-автоматів. Перший верстат робітник запустив о 8год (початок зміни), а кожний наступний на 2хв пізніше. Визначте в метрах об’єм продукції, зробленої за семигодинну зміну, якщо продуктивність кожного верстата дорівнює а м/год.

Вчитель: В біології прогресії пов’язані з такими темами, як розмноження, поділ клітин, формені елементи крові та інші. Неможливо розв’язати біологічні задачі з даних тем, не використавши знання про прогресії. За теорією еволюції Дарвіна, всі процеси, які пов’язані з живими організмами, відбуваються прогресивно або регресивно.

Як впливає кількість еритроцитів на самопочуття людини?

Вашій увазі пропонується задача № 5 (Сдайд 12)

Задача № 5. Кількість еритроцитів ( з розрахунку на 1 мм³) в крові людини становить на рівні моря – 5 мільйонів. Через кожні 600 м підняття в гору їх кількість збільшується на 1 мільйон. Яка кількість еритроцитів буде в крові людини, якщо вона підніметься на вершину гори Еверест (4800 м) . Чому це відбувається?

Застосуйте ваші знання з математики.

Вчитель: Проаналізуємо цю задачу. В чому математична суть і яка математична модель цієї задачі? (Розв’язування задачі письмово. Учні після обговорення записують самостійно, а потім перевіряють)

5, 6, 7, 8, … Що це за послідовність? (АП)

Що дано? Що знайти?

a₁=5, d = 1, h = 4800, h₁ = 600, a_n - ? (Слайд 13)

За якою формулою будемо обчислювати a_n?

Чого не вистачає для обчислень за цією формулою?

Як знайти п?

n = 4800 : 600 = 8, (Слайд 13)

Обчисліть самостійно а₈. Перевірте.

a₈ = a₁ + 1(n – 1) = 5 + 7 = 12 (млн) (Слайд 13)

Відповідь: 12 млн

Вчитель: Чому це відбувається?

У зв’язку з розрідженим повітрям в легені повинно більше потрапляти кисню, відповідно цьому збільшується кількість еритроцитів.

Вчитель: Процес розмноження відбувається прогресивно.

Спробуємо розв’язати таку проблему. (Слайд 14)

Задача № 6 (письмово). Уявімо, що на початку нашої ери жінка М народила дві доньки, кожна з них до 30 років народила теж дві доньки і т.д. Чи можливо це? Скільки б за таких умов нащадків М жило б у наш час?

Вчитель: Проаналізуємо цю задачу. В чому математична суть і яка математична модель цієї задачі?

На початку ери 2, через 30 років 4, через 40 років 8, … (Слайд 14)

1, 2, 4, 8, 16, 32, … Що це за послідовність? (Геометрична прогресія) … (Слайд 15)

Що відомо?

b₁= 1, q = 2, час – 1000 років, період – до 30 років, (Слайд 15)

Що знайти?

S_n -? … (Слайд 15)

(Учні розв’язують цю задачу на дошці та в зошитах, а потім перевіряють)

n = 1000 : 30 34

. … (Слайд 15)

Вчитель: Чи можливо це?

Відповідь: 73786976294838206464

Висновок: це число значно перевищує кількість людей на планеті. Тому це не можливо. (Слайд 15)

Вчитель: На початку вивчення теми ми розглядали задачу, яку залишили без розв’язання, бо тоді нам не вистачило знань, щоб розв’язати її. А зараз ми повернемося до неї. (Слайд 16)

Задача 12. Задача про розмноження бактерій.

За сприятливих умов за 1 хв кожна з бактерій поділяється навпіл. Визначити кількість бактерій, народжених однією бактерією за 7 хв.

Розв'язання:

Кількість бактерій зростає за геометричною прогресією:

2, 4, 8, 16, ..., у якої .

=2(27-1 )=2( 128-1 )=2 127=254(бактерії).

Задача 7. Бактерія, потрапивши в організм людини, до кінця 20-ї хвилини ділиться на 2, кожна з них через 20 хв ще на дві і т.д. Скільки бактерій стане в організмі людини через добу?

Що маємо?

1, 2, 4, 8, 16, … - геометрична прогресія, (Слайд 17)

Що дано?

b₁ = 1, q = 2, час – 1 доба (Слайд 17)

Що знайти?

S_n (Слайд 17)

Розв’язання

хвилин у добі 60 х 24 = 1440 (хв.), n = 1440 : 20 = 72,

Відповідь: (Слайд 17)

Вчитель: Можете уявити собі, що робиться в вашому організмі через добу! Ця задача закликає вас не нехтувати правилами власної гігієни.

Вчитель: Не тільки в біології ми можемо зустрітися з прогресіями. Рух ми вивчаємо у … (фізиці)

Вашій увазі пропонується задача (письмово). (Слайд 18)

Задача № 8 . Гальмуючи, автомобіль за першу секунду проїхав 15 м, а за кожну наступну – на 3 м менше, ніж за попередню. Знайдіть гальмівний шлях автомобіля.

Що дано? a₁=15, d = -3, a_n = 0, (Слайд 19)

Що знайти? S_n - ? (Слайд 19)

Розв’язання. Як знайти п? Яку формулу використати?

a_n= a₁ + d(n – 1),

15 – 3(n -1) = 0,

n = 6,

S₆ =

Відповідь: 45 м. (Слайд 19)

Вчитель: Ця задача застерігає кожного з нас, що треба бути уважним на дорозі.

VІІ. Підсумок роботи над проектом

задачу на прогресію або задачу практичного чи гумористичного змісту.

Задача про поділ хліба з єгипетського згортка Ринда. Сто мір хліба поділили між п'ятьма особами так, щоб другий отримав більше від першого на стільки, на скільки третій більше від другого, третій більше за четвертого та п'ятий більше за шостого. Крім того, двоє перших мають отримати в 7 разів менше від трьох останніх. Скільки отримав кожний із них? (стародавня задача)
Тіло у разі вільного падіння проходить за першу секунду 4,9 м, а за кожну наступну на 9,8 м більше. Знайти глибину шахти, якщо тіло, що вільно падає, досягає дна через 5 с після початку падіння. (фізика) (44,1 м)
Язиката Хвеська протягом місяця (31 день) щодня розповідає в сільському клубі анекдоти про політику. Через утому кожного наступного дня кількість анекдотів на 2 менше, ніж попереднього. Скільки анекдотів почули від Хвеськи односельці, якщо першого дня вона розказала їх рівно 100? (задача гумористичного змісту)
Винагорода воїна (задача з російського підручника, 1795 р). Воїну, що служив, дано винагороду: за першу рану — 1 копійка, за другу — 2, за третю — 4 і т.д. Виявилося, що воїн одержав винагороду 655 руб. 35 коп. Запитується, яка кількість його ран.(стародавня задача) (40)
Побудова теплиці. Потрібно виготовити вертикальні стержні для теплиці з дроту так, щоб найменший мав довжину 5 дм, а кожний наступний був на 2 дм довший (до 7-го стержня). Обчисліть довжину дроту, необхідну для виготовлення стержнів. (Задача практичного змісту) (77 дм)
Первинний внесок 400 грн банк щорічно збільшує на 15 %. Яким стане внесок через 4 роки? (економіка)
У коло радіусом 4 см вписано квадрат, у який знову вписано квадрат та коло і т. д. Знайдіть суму довжин усіх таких кіл. (Геометрія)
Це було майже 100 років тому. Селянин продав 20 овець за 200 крб. Коли один із покупців почав довго торгуватися, селянин запропонував: «Заплати за одну вівцю 1 к., за дві вівці — 2 к., за три — 4 к. і далі за кожну вівцю вдвічі більше копійок, ніж за попередню». Покупець погодився. Скільки грошей заплатив він за 20 овець? (Стародавня задача)
Бактерія, потрапивши в організм, на кінець 20-ї хвилини поділяється на дві, кожна з них на кінець 20-ї хвилини знову поділяється на дві і т. д. Скільки бактерій буде в організмі через добу? (Біологія)

Зрозуміло, що підібрані задачі не всі стосуються арифметичної прогресіїї, деякі з них відносяться до наступної теми, яку ми будемо вивчати це – геометрична прогресія. (створена проблема, яку буде розв’язано на наступних уроках)

У період інтенсивного зростання людина росте в середньому на 5см за рік.Зараз ріст Олексія – 170 см.Якого росту він буде в 2026 році?Задача 6. Кожний курець викурює в день у середньому 8 сигарет.Після викурювання першої сигарети в легенях осідає 0,0002 г. нікотину й тютюнового дьогтю. З кожною наступною сигаретою ця кількість збільшується на 0,000001 г. Яка кількість шкідливих речовин осідає в легенях за рік?(Відповідь: 4,846 г.).

Ян Амос Коменский говорив: «Уважай нещасним той день або ту годину, у яку ти не засвоїв нічого нового, нічого не додав до свого розвитку».

Задача 1(усно). Кількість еритроцитів ( з розрахунку на 1 мм3) в крові людини становить на рівні моря – 5 мільйонів. Через кожні 600 м підняття в гору їх кількість збільшується на 1 мільйон. Яка кількість еритроцитів буде в крові людини, якщо вона підніметься на вершину гори Еверест (4800 м) Чому це відбувається?

Застосуйте ваші знання з математики.

Розв’язання

Проаналізуємо цю задачу. В чому математична суть і яка математична модель цієї задачі?

Дана задача розв’язується за допомогою арифметичної прогресії, у якої :

а1 = 5, d =1,n = 8 .

Використавши формулу n – го члена арифметичної прогресії, одержимо:

а8 = а1 + (8-1) d = 5 + 7 = 12.

Задача 3 (письмово). Уявіть, що ви хочете взяти в банку кредит у розмірі 3000грн. За перший день ви будете зобов’язані заплатити банку 1 коп., за другу – 2ко.п, за третій – 4 коп. і т. д. Чи укладете ви з цим банком договір не менше, ніж на 20 днів?

Розв’язання

Суми виплатів за кожен день, утворюють геометричну прогресію 1, 2, 4, 8, … , у якій b1 = 1, q = 2, n = 20. Використаємо формулу для обчислення суми n перших членів геометричної прогресії: Sп = , S20 =524288коп.

Розв’язавши дану задачу, ми бачимо, що умови такого кредиту для клієнта банку є невигідними

Вчитель: Проаналізуємо цю задачу. В чому математична суть і яка математична модель цієї задачі?

На початку ери 2, через 30 років 4, через 40 років 8, … (Слайд 14)

1, 2, 4, 8, 16, 32, … Що це за послідовність? (Геометрична прогресія) … (Слайд 15)

Що відомо?

b1 = 1, q = 2, час – 1000 років, період – до 30 років, (Слайд 15)

Що знайти?

Sn -? … (Слайд 15)

(Учні розв’язують цю задачу на дошці та в зошитах, а потім перевіряють)

n = 1000 : 30 ≈ 34

S_n=(b_1 (q^n-1))/(q-1).

S_34=(1(2^34-1))/(2-1)=2^34=73786976294838206464. … (Слайд 15)

Вчитель: Чи можливо це?

Відповідь: 73786976294838206464

Висновок: це число значно перевищує кількість людей на планеті. Тому це не можливо.

Задача групи 3

Задача від банка. Ви хочете узяти у банку кредит на 10000 гривень. Умови кредитування: за перший день ви маєте сплатити фірмі 1 копійку, за другий – 3 копійки, за третій – 9 копійок і т.д. Чи уклали б ви з цим банком договір не менше ніж на 30 днів?

Страница 192 | Учебник Фізика 9 класс В.Г. Бар’яхтар, Ф.Я. Божинова, С.О. Довгий 2017 №1№2