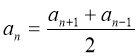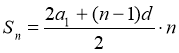Конспект уроку "Арифметична прогресія"

Міністерство освіти та науки України

Інформаційно-методичний центр відділу освіти

Самбірської райдержадміністрації

 

 

 

 

Виконавець:

вчитель математики та інформатики

Чайковицького НВК « СЗШ І-ІІІ ст. - ДНЗ»

ВАСИЛИШИН ЛЮБОВ ФЕДОРІВНА

 

 

Чайковичі – 2015

ТЕМА УРОКУ:    АРИФМЕТИЧНА ПРОГРЕСІЯ ТА ЇЇ ЗАСТОСУВАННЯ

Мета уроку:

• Навчальна – продовжити роботу над визначенням  арифметичної прогресії; формулами n-го члена, суми n перших членів; характеристичними властивостями, які мають члени прогресії; виробити загальні рекомендації з виконання завдань, що містить дана тема. сприяти розвитку вміння самостійно здобувати знання, використовуючи різні інформаційні технології; вміння оцінювати свої досягнення, показати практичне застосування теми  на прикладах історичних задач;

• Розвиваюча – розвивати вміння й навички застосовувати формули прогресії при розв'язуванні задач; продовжити подальшу роботу з вироблення вміння порівнювати математичні поняття, знаходити подібності й відмінності, уміння спостерігати, помічати закономірності, проводити міркування за аналогією.
•  Виховна – сприяти підвищенню інтересу до математики, активності, умінню спілкуватися, аргументовано відстоювати свої міркування.

Тип уроку:  урок формування знань вмінь і навичок

Обладнання на уроці: комп'ютер,  мультимедійний проектор

Програмне забезпечення: операційна система Windows ХР, MS Word, MS Excel, MS Power Point, тестуюча система Test W2-v1.4

ХІД УРОКУ

І. Мотивація навчальної діяльності учнів

Слово “прогресія” походить від латинського слова “progressio” і означає “рух уперед” (як і слово “прогрес”). Уперше цей термін як математичний вживається у працях римського вченого Боеція (V – VI ст.).

Перша умова, якої треба дотримуватися в математиці, – це бути точним.  Друга – бути чітким, і наскільки можливо, простим.

Отже, ми сьогодні з вами на уроці просто, чітко і з легкістю повторимо знання з теми: « Арифметична прогресія», закріпимо навички обчислення елементів прогресії, покажемо практичне застосування теми на прикладах історичних задач, задач практичного змісту, будемо удосконалювати вміння оцінювати свої досягнення.

Що означають фрази?

«Частка пенсіонерів у країні росте в арифметичній прогресії…»

« При зростаючій відносній масі ракети … швидкість ракети росте в арифметичній прогресії…»

Давайте згадаємо визначення арифметичної прогресії й основні формули.

 

ІІ. Перевірка домашнього завдання

1) «Мікрофон»

1. Дайте визначення арифметичної прогресії.
2. Як називають стале число d для такої послідовності?
3.  Чому дорівнює число d ?
4. Як перевірити чи є число членом арифметичної прогресії? ( Якщо різниця між наступним і попереднім членом послідовності одне й теж число, то дана послідовність є арифметичною).
5. Назвіть формулу n-го члена арифметичної прогресії.
6. У чому полягає характеристична властивість арифметичної прогресії. (Кожний член арифметичної прогресії, починаючи із другого рівний середньому арифметичному двох сусідніх з ним членів).
7. Назвіть формули суми п-перших членів арифметичної прогресії.
8.  За якою формулою можна знайти будь-який член арифметичної прогресії?
9.  Якою є арифметична прогресія, якщо d < 0, d > 0,    d = 0?
10. Як перевірити, чи є послідовність арифметичною прогресією?
11.  Що можна знайти в арифметичній прогресії, знаючи d   та а₁ ?

 

Названі формули занесемо в таблицю.

	Арифметична прогресія
Визначення
Формула n-го члена
Характеристична властивість
Формула суми n членів

 

 

2) «Перевір себе!»      

Які з послідовностей є арифметичними прогресіями?

1.  3, 6, 9, 12,…..   
2.  5, 12, 18, 24, 30,…..        
3.  7, 14, 28, 35, 49,….
4.  5, 15, 25,….,95….
5.  1000, 1001, 1002, 1003,….
6.  1, 2, 4, 7, 9, 11…..

7)   5, 4, 3, 2, 1, 0, -1, -2,….

3) «Обчисли усно»

  Знайди різницю арифметичної прогресії:

1)  1; 5; 9………

2)  105; 100;95….

3)  -13; -15; -17……

4)   11;?; 19,….

4) «Розв'яжи задачу»

Між числами 6 і 21 вставте 4 числа так, щоб разом з даними числами вони утворювали арифметичну прогресію.

Розв'язок:     а₁ = 6,    а₆ = 21,

d = (21 – 6)/ (6 – 1)= 3,

6, 9, 12, 15, 18, 21.

 

ІІІ. А зараз ми проведемо тестування за допомогою ПК і карток

 (Сильніші учні класу працюють за комп’ютерами, відповідаючи на запитання у програмі Test W2-v1.4. У кінці роботи комп’ютер видає одержану кількість балів. Слабша частина учнів працює на місцях на  картках) 

 

 

Тести

1.      З вказаних послідовностей арифметичною прогресією є...

     а) 45; 15; 5; 0...;            б) 4; 9; 9; 4...;        

     в) 2; 4; 8; 16...;              г) 15; 17; 19; 21...

 2.  Якщо перший член арифметичної прогресії дорівнює 8, а різниця 3, то другий її член дорівнює...

                    а) 5;       б) 24;       в) 8/3;         г)  11

3.   Якщо третій член арифметичної прогресії    дорівнює 15 і різниця 4, то четвертий її член дорівнює...

   а)  11;      б) 60;     в) 19;      г) 15/4

4. У заданій арифметичній прогресії 3; 7; 11; 15 другим членом є число...

   а) 3;         б) 7;         в)  10;         г) 4

5. Якщо арифметична прогресія (an) зростаюча, то...

     а) а₁ < а₂;  б) а₁ > а₂;   в) a₁ = a₂;    г) а₁ ≥ а_2;    г) інша відповідь.

6.  Щоб знайти різницю арифметичної прогресії 4; 7; 10; 13;..., треба...    

         а) 4 + 7;      б) 4 • 7;       в) 4 – 7;     г) 7 – 4

7. Щоб обчислити а₁₁, якщо а₁ =3, d = 8, необхідно...

     а) 3+(8-1)11;        б)   8+(11–1)3;   

в) 3+(11-1)8;        г) 8+(3–1)11

 

 8.  Якщо задана арифметична    прогресія і а₁ +а₂₁ = 54, то сума а₂ +а₂₀  дорівнює...

            а) 22;    б) 18;     в) 54;    г) 108.

 9.  Якщо а₁ =11, а₁₅ =89, то,  щоб  обчислити S₁₅, треба...

            а)   (15+11)/2*89;          б) (15+89)/2*11;

            в)   (15+11)/89*2;          г) (89+11)/2*15

 

10. Кого із вчених називали “Королем математики”

          а) Ломоносова;    б) Гаусса;   

          в) Піфагора;         г) Галілея.

 

ПРІЗВИЩЕ та ІМ’Я ___________________________________

 

IV. Із історії арифметичної прогресії

 

Прогресії як часткові види числових послідовностей, трапляються в папірусах ІІ тисячоліття до н. е. Перші із задач на прогресії, що дійшли до нас, пов’язані з господарською діяльністю, а саме – з розподілом продуктів, поділом спадку тощо. Перші спогади про арифметичну прогресію були ще у прадавніх народів. У клинописних вавилонських табличках і єгипетських папірусах зустрічаються задачі на прогресії та вказівки як їх розв’язувати.

Вважалось, що в давньоєгипетському папірусі Ахмеса перебувала найдавніша задача на прогресії про поділ ячменю “Нехай тобі сказали: розділи десять мір ячменю між 10 чоловіками так, щоб різниця між кожним чоловіком і його сусідом становила 1/8 міри ячменю ”.

Нехай І чоловік отримав х міри ячменю, а різниця у= . Тоді 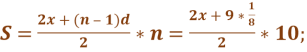*10=10; 16x+9=16; 16x=7; x=

1чол.-; 2 чол.-; 3 чол. - ; 4 чол. -; 5 чол. -; 6 чол. –  = 1;  7 чол. -1 ; 8 чол. - 1 ; 9 чол. - 1; 10 чол. - 1  .

 

Але є набагато більш стара задача про ділення хліба, яка записана в знаменитому єгипетському папірусі Ринда. Папірус цей, розшуканий Риндом піввіку назад, складений близько 2000 років до нашої ери і є списаним з іншого, ще більш прадавнього математичного твору, що відноситься, можливо, до третього тисячоріччя до нашої ери.

Задача: (задача з папірусу Ринда)

Сто мір хліба розділили між 5 людьми так, щоб другий одержав на стільки ж більше першого, на скільки третій одержав більше другого, четвертий більше третього й п'ятий більше четвертого. Крім того, двоє перших одержали в 7 раз менше трьох інших. Скільки потрібно дати кожному?

Розв'язок задачі:

Зрозуміло, що кількість хліба, яку отримав кожен з учасників розділу, становить зростаючу арифметичну прогресію. Нехай перший її член x, різниця y. Тоді:

•                  а ₁–Частка першого – x,
•                  а₂–Частка другого – x+y,
•                  а₃–Частка третього – x+2y,
•                  а₄–Частка четвертого – x+3y,
•                  а₅–Частка п'ятого – x+4в.

На підставі умови задачі складаємо наступні 2 рівняння:

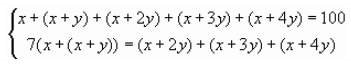
Після спрощень перше рівняння має вид x+2y = 20, а друге 11x = 2y. 12х=20, х=1. У=(20 - 1):2=; 1 людина - 1; 3 люд. – 20; 4 люд. - ; 5 люд.- .

 

У папірусі подається не тільки текст задачі, але й пропонується правило для обчислення частки першої з десяти осіб.

Це правило, виражене мовою сучасних формул, має вигляд:

 

 

З досліджень вавилонських клинописних текстів епохи Хаммурані (XVIII cт. до н. е.) бачимо, що і в стародавньому Вавилоні розв’язування деяких питань господарського і наукового характеру приводило до арифметичної прогресії.

 

Ось одна з таких задач:“10 братів; 1 2/3 міни срібла; брат над братом піднімається; на скільки піднімається, я не знаю. Частка восьмого 6 мехелів. Брат над братом на скільки піднімається? Яка частка кожного брата?”(1 2/3 міни становлять 100 мехелів).

Розв’язання

Нехай х – частка першого брата, а d – на стільки піднімається брат над братом

Тоді *10=100; 2x+9d=20; а₈  =х+7d=6; х=6-7d; 2(6-7d)=20; 12-14d+9d=20; -5d=8; d=-1,6. Х=6+11,2=17,2 мел.

1 брат – 17,2 мел., 2 брат – 15,6 мел.; 3 брат – 134 мел.; 4 брат – 12,4 мел. 5 брат – 10,8 мел.; 6 брат – 9,2 мел.; 7 брат – 7,6 мел.; 8 брат – 6 мел.; 9 брат – 4,4 мел.  і 10 брат – 2,8 мел. 

 

   У нас задачі на прогресії вперше зустрічаються в одній з найдавніших пам’яток руського права, в “Руській правді”, складеній при Ярославі Мудрому в ХІ столітті. Там є стаття, присвячена обчисленню приплоду від 22 овець за 12 років, при умові, що кожна вівця щорічно приносить одну овечку і одного барана.

Там же можна прочитати складений сільським господарем цікавий розрахунок приплоду за 12 або 9 років від усієї худоби і бджіл його села, прибутку від посіяних хлібів і п’яти скирт сіна, а також розрахунок плат за дванадцятирічну сільську роботу жінки з дочкою

 

         

 

Значна кількість задач на прогресії міститься  в чудовій пам’ятці математичної літератури початку XVIII cт. “Арифметиці” Л. П. Магніцького.

Протягом півстоліття ця книга була основним математичним підручником в Росії. М.В. Ломоносов дуже високо цінив книгу Л.П. Магніцького, називаючи її “вратами ученості”.

        

 

В цій книжці була ось така задача „ Хтось продавав коня. Просив за нього 25 рублів. Купець, що побажав купити, обурився, що дорого. „Добре, - відповів продавець. Бери коня даром, а заплати тільки за цвяхи на його підковах. А цвяхів у всякій підкові 6 штук. І будеш ти мені платити за них у такий спосіб: за перший цвях 10 копійок, за другий цвях 20 копійок, за третій – 30 копійок і т.д.” Купець же, думаючи, що заплатить набагато менше, чим 25 рублів, погодився. Чи проторгувався купець, і якщо так, то на скільки?”

Розв’язання

а₁= 10 коп., а d = 10 коп.  Всіх цвяхів у коня 6*4=24 цвяхи. Знайти S₂₄

S₂₄==*24= 250*12= 3000 коп.=30 руб.

Купець проторгувався на 5 рублів.

Відомий німецький математик Карл Гаусс (1777 - 1875) ще у школі виявив блискучі математичні здібності.  Коли йому було 9 років, учитель, прагнучи надовго зайняти дітей, задав на уроці наступну задачу: знайти суму перших ста натуральних чисел. На здивування учителя один з учнів (це був маленький Гаусс ) через хвилину викликнув: “Я вже розв'язав”. У зошиті Гаусса було тільки одне число, але зате вірне. Як міркував маленький Гаусс? Зміркувавши, що суми 1+100, 2+99 і т. д. рівні, він помножив 101 на 50, тобто число таких сум , яке дорівнює 5050. Інакше кажучи, він помітив закономірність, яка властива арифметичній прогресії.

 

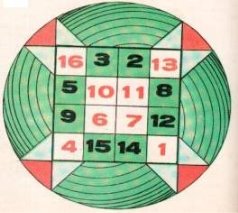
                  Я розповім про чудового математика на прізвище Рамсей.  Він жив на початку ХХ століття. Ним була створена теорія, що доводить, що у світі немає абсолютного хаосу. Що навіть,  сама неупорядкована система має певні математичні закономірності. Згадайте, коли ви дивитеся на зірки, то може здатися, що розташовані вони в самому випадковому порядку. Але ще в стародавні  часи люди побачили там сузір'я Риб і Касеопеї, Лева й Оріона.

            Перед вами картки. Будь-ласка, запишіть цифри від 1 до 9, замалюйте 4 з них в якому-небудь порядку. Але Рамсей довів, що це не так.  Зверніть увагу, що хоча б три які- небудь числа одного кольору обов'язково складають арифметичну прогресію. Випишіть ці числа. Що ви побачили? Три із них утворюють арифметичну прогресію.

1  2  3  4  5  6  7  8  9;     1  2  3  4  5  6  7  8  9

 

«Цікава властивість арифметичної прогресії».

Дана „зграйка дев'яти чисел”:

3, 5, 7, 9, 11, 13, 15,17, 19.

 Вона являє собою арифметичну прогресію. Крім того, дана зграйка чисел приваблива здатністю розміститися в дев'яти клітках квадрата 3х3 так, що утворюється магічний квадрат з константою, рівної 33.

Чи знаєте ви, що таке магічний квадрат? Квадрат, що полягає з 9 кліток, у нього вписують числа, так щоб сума чисел по вертикалі, горизонталі, діагоналі була тим самим числом- constanta. Зауваження про арифметичну прогресію само по собі дуже цікаво. Справа в тому, що з кожних дев'яти послідовних членів будь-якої арифметичної прогресії натуральних чисел можна скласти магічний квадрат.

 

9	19	5
7	11	15
17	3	13

 

З якої послідовності чисел складений цей магічний квадрат?

 

 

 

 

 

 

 

Пошукова робота учнів

VI. Захист учнівських проектів. (Презентації додаються)

Сьогодні ви навчитеся розв’язувати ряд задач практичного змісту за допомогою арифметичної прогресії, використовуючи комп’ютери та програму Excel.

VIІ.  Розв’язування задач практичного змісту

Задача 1. Курс повітряних ванн починають із 15 хв. у перший день і збільшують час цієї процедури в кожний наступний день на 10 хвилин. Скільки днів слід приймати ванни в зазначеному режимі, щоб досягти їхньої максимальної тривалості 1 година 45 хвилин?

Дано: арифметична прогресія, а₁=15 хв, d = 10 хв., a_n =105 хв. Знайти:   n

Розв'язання

а_n = а₁ + (n-1)*d;     15+10(n-1)=105; 10*n = 100;  n = 10

Відповідь: 10 днів слід приймати ванни.

Задача 3. Робітник виклав плитку в такий спосіб: у першому ряді - 3 плитки, у другому - 5 плиток і т.д., збільшуючи кожний ряд на 2 плитки. Скільки плиток потрібно для 7 ряду? Скільки всього потрібно плиток ? ( задачу розв’язати в Excel).

Розв'язання

а_n = а₁ + (n-1)*d; а₇ = 3 + 6*2 = 15 плиток. S_n = (2* а₁ +(n-1)*d):2*n; S₇ = (2* 3 +6*2):2*7 = 63 плитки

Відповідь: 63 плитки

Задача 4. При вільному падінні тіло проходить за першу секунду 4,9 м, а за кожну наступну на 9,8 м більше. Знайти глибину шахти, якщо вільно падаюче тіло, досягло її дна через 5 с від початку падіння (фізика). ( задачу розв’язати в Excel).

      а₁=4,9 м, а d=9,8 м. Знайти S₆.  S₆ = (2а₁ + (n-1)*d):2*5;  S₆ =(2* 4,9 + (5-1) *9,8) :2* 5 = 122,5 м

Відповідь: 122,5 м

Задача 5. У період інтенсивного зростання людина росте в середньому на 5 см у рік. Зараз ріст Олексія – 130 см. Якого росту він буде в 2026 році? ( задачу розв’язати в Excel).

Розв’язання

а_n = а₁ + (n-1)*d; а₁₁ = 130 + 5*10 = 180 см

Відповідь: 180 см

Задача 6. Кожний курець викурює в день у середньому 8 сигарет. Після викурювання першої сигарети в легенях осідає 0,0002 г. нікотину й тютюнового дьогтю. З кожною наступною сигаретою ця кількість збільшується на 0,000001 г. Яка кількість шкідливих речовин осідає в легенях за рік?    ( задачу розв’язати в Excel).

Розв’язання

Курець викурює за рік 365*8 = 2920 сигарет. S_n = (2* а₁ +(n-1)*d):2*n; S₂₉₂₀ = (2* 0,0002 +2920*0,000001):2*2920 = 4,847 г

Відповідь: 4, 847 г

 

Задача 7.  Язиката Хвеська протягом мі­сяця (31 день) щодня розпо­відає в сільському клубі анек­доти про політику. Через утому кожного наступного дня кіль­кість анекдотів на 2 менше, ніж   попереднього. Скільки анекдотів почули від Хвеськи односельці, якщо першого дня  вона розказала їх рівно 100? (задача гумористичного змісту) ( задачу розв’язати в Excel).

Розв’язання

а₁= 100 анекд, а d= - 2 анекд. Знайти S₃₁.

S₃₁==*31= 70*31= 2170 анекдотів

Відповідь: 2170 анекдотів

Задача 8.  Побудова теплиці

 Потрібно виготовити вертикальні стержні для теплиці з дроту так, щоб найменший мав довжину 5 дм, а кожний наступний був на 2 дм довший (до 7-го стержня). Обчисліть довжину дроту, необхід­ну для виготовлення стержнів. ( задачу розв’язати в Excel).

Розв’язання

а₁= 5 дм, а d= 2 дм.  Знайти S₆.

S₆==*6= 10*6= 60 дм

Відповідь: 60 дм

Задача 2

Дама здавала в багаж:

Диван ………..  кг

Чемодан…   21 кг

Саквояж…….   кг          арифметична

Картину…   18 кг              прогресія

Корзину……..  кг

Картонку……..кг

                 І собачечку…….. кг               Знайти вагу багажу.

Розв'язання

a_{2 =}  а₁ + d;  а_{1 =}   a₂ – d;  a_{4 =}  а₁ + 3d; ;  а_{1 =}  a₄ - 3d; a₂ – d = a₄ - 3d; a₂ – a₄= d - 3d;

-2d= 21-18; d= - 1,5.  Диван = а₁=21 – (- 1,5) = 22,5 кг. Саквояж = 18 – (-1,5) =19,5 кг; корзина=18-1,5=16,5 кг; картонка=16,5-1,5=14,5 кг; і собачка= 14,5-1,5= 13 кг. S= 126 кг

Відповідь: 126 кг

 Задача 9. Риболовля

Олег, Петро, Сергій та Андрій ловили рибу. Кількості рибин, які вони впіймали, утворюють арифметичну прогресію. Найменше рибин – 9 – упіймав Петро, а найбільше – 18 – Олег. Скільки рибин упіймали Сергій та Андрій разом? Скільки всього рибин упіймали хлопці?

Розв'язання

В арифметичній прогресії а₁₊ а_{n =} а_{2 +} а_{n-1 =} а₃₊ а_n-2. Тому Сергій та Андрій разом зловили 9+18=27 рибин. Хлопці зловили 54 рибини.

Задача 10. Птахи

Зграя птахів летіла на південь. За перший день ця зграя птахів пролетіла 201 км, а за другий день на 2 км більше, ніж  за попередній. За скільки днів перелітні птахи долетять до місця зимівлі, якщо перелітний шлях рівний 4641 км?

Розв'язання

Перелітний шлях зграї птахів утворює арифметичну прогресію, в якій а₁= 201 км, S_n = 4641 км, d=2 км. S₆ ==*n = 4641;   200*n+n²=4641;   n² + 200*n – 4641 = 0; n = 21 день

Відповідь: 21 день

Задача 11. Піраміди для фараонів

Будуючи піраміди для фараонів, єгиптяни в кожному наступному ряду плит встановлювали на одну плиту менше, ніж в попередньому. На самому верху стіни підноситься одна плита. Скільки всього плит знадобиться тільки для однієї стіни піраміди, якщо плити стоять в 60 рядів?

Розв'язання

a_n = а₁+59* (-1) = 1; а₁= 1+59=60 пл.

 S₆ ==*60 = 3660 пл.

Відповідь: 3660 плит

Задача 12. Про приріст косуль

Раніше поширені скрізь косулі збереглися лише місцями. Їх поголів’я, яке складало більше мільйона особин різко скоротилося: у 1990 році їх залишилося трохи більше 15000. Проте завдяки захисним заходам, прийнятим відносно цього виду в 2005 році їх чисельність досягла 60010 особин. Скільки особин поповнювало ряди косуль в середньому щороку?

Розв'язання

а₁₅ = а₁+14d; 14d = 60010-15000=45010;  d = 45010: 14 = 3215 косуль.

Відповідь: 3215 косуль

Задача 13. Криниця

Людям, які копають криницю, обіцяно за перший метр заплатити 30 грн., а за кожний наступний на 20 грн. більше, ніж за попередній метр. Скільки вони одержать за копання 12 метрової криниці? (задачу розв’язати в Excel).

Розв'язання

  S₁₂ = (2а₁ + (12-1)*d):2*12=( 60+11*20):2*12= 140*12=1680 грн.

Відповідь: 1680 грн

Задача 14. Штангіст

Штангіст піднімає штангу вагою 45 кг. З кожним підходом вага штанги збільшується на 5 кг. Скільки кг підніме штангіст за 7 підходів? (задачу розв’язати в Excel).

Розв'язання

  S₇ = (2а₁ + (n-1)*d):2*n = ( 90+6*5):2*7= 60*7 = 420 кг

 Відповідь: 420 кг

 

Задача 15. Колоди

 

При зберіганні колод будівельного лісу їх укладають так, як показано на малюнку. Скільки колод знаходиться в одній кладці, якщо в її основу покласти 12 колод?

(Розв’язати задачу в Еxcel)

Розв’язання

а₁= 12 колод, d = -1. n = 12. Знайти S_12.   S₁₂ = (2а₁ + (12-1)*d):2*12 = (24+11*(-1)):2*12 = 78 колод

Відповідь: 78 колод.

 

VIІІ.  Літературна сторінка

 

Ода математичній прогресії

 

Будь-яка прогресія

Рухає прогрес.

До мети завітної

Вчений йде й поет.

Навіть у свідомості

Світлі лиш думки

  Будуть прогресивніші

За лихі та злі.

 

                                                                     А у математиці

                                                                          Їх живе аж дві,

                                                           Додавання й множення

                                                               Здійснюють вони.

 

Та виходять числа ті

Зовсім не прості.

От якби грошима,

Всі були б круті!

 

А вона у фізиці                     

В поділі ядра

Ділить його навпіл,

Потім їх на два. 

                                              

 А у біології

Без її умінь

Не було б розмноження:

Вимер цілий світ!

                     

Правильний трикутник,

В ньому ще один –

Все це теж прогресії

        Чудодійний вплив. 

 

                  

 Мучився б із віршами

Кожен в нас поет,

Якби не прогресія

Ямб знайшла й хорей.

 

Тож вивчаймо й знаймо            

Цей закон усі,

Неодмінно будемо                

Мудрими тоді!

 

 

Вірш про   ПОСЛІДОВНІСТЬ

 

Послідовність, послідовність

 ми вивчаємо на совість.

Ми знаходимо в задачах

  навіть числа Фібоначчі.

Всі ми формули впевнено знаємо,

 всі навчились знаходити S,

І, до речі, «прогресія» має

  спільний корінь зі словом «прогрес»!

Ми прогресії вивчали,

 в них  цікавинок  чимало!

Особливо здивувало

швидко суми як зростали.

Ось покладемо на шахівницю

 ми зернину, а потім і дві.

В сумі ж стільки потрібно пшениці,

 що не знайдеться і на землі!

 

Ми прогресії вивчали.

В них властивостей чимало!

І коли вона зростає,

в класі кожен учень знає.

 

В послідовностях  щастя й удачі

ми бажаємо додатного d.

Ця прогресія так чи інакше

по життю хай вперед нас веде.

 

                    Чеський педагог Ян Амос Коменский говорив:

«Вважай  нещасним  той день або ту годину, в яку ти не засвоїв нічого нового, нічого не додав до свого розвитку».

 

 

Я сподіваюсь, що на сьогоднішньому уроці ви знайшли для себе хоч краплинку нового і корисного.

 

 

 

VII. Підсумок уроку. (Учні підсумовують свою роботу)

1. Що нового ви дізналися на уроці?
2. Чи досягли очікуваних результатів?

VIIІ.  Домашнє завдання

1. Підготуватись до письмової самостійної роботи.
2. Придумати по 2 задачі практичного змісту на арифметичну прогресію та розв’язати їх.