Урок+презентації. Алгебра 9 клас: "Геометрична прогресія. Формула n-го члена геометричної прогресії"

Новооржицька ЗОШ І-ІІІ ступенів

Урок з алгебри у 9 класі

Учитель Яцько М. М.

2018

Тема уроку: Геометрична прогресія, її властивості. Формула n-го члена геометричної прогресії.

Мета уроку:

навчальна: Навчити учнів застосовувати формулу n-го члена геометричної прогресії, систематизувати та узагальнити знання учнів по даному матеріалу;

виховна: Виховати охайність запису в зошитах та на дошці, сприяти вихованню культури обчислень, інтересу до уроку.

Тип уроку: комбінований

Обладнання: комп’ютер, проектор, дошка, Microsoft Office PowerPoint.

План уроку

1. Організаційний момент 2 хв.
2. Актуалізація опорних знань 8 хв.
3. Вивчення нового матеріалу                              12 хв.
4. Розв'язування задач. 19 хв.
5. Підведення підсумків                                  3хв.
6. Повідомлення домашнього завдання 1 хв.

«Недостатньо мати добрий розум, головне –

це раціонально застосувати його».

Р. Декарт

Хід уроку (Слайд 1)

І. Організаційний момент.

На сьогоднішньому уроці ми розглянемо розв’язання різноманітних задач, узагальнимо і систематизуємо наші знання з теми «Арифметична прогресія та числова послідовність»  та проведемо тестовий контроль з метою встановлення  рівня  усвідомлення навчального матеріалу. Запишіть число і тему уроку.

Мотивація навчальної діяльності. (Слайд 2)

«Перша умова, якої треба дотримуватися в математиці, –

це бути точним, друга – бути чітким,

і наскільки можливо, простим». Л.Карно.

І сьогодні на уроці ми побачимо, як можна застосувати вивчене Вами з даної теми в різних галузях.

ІІ. Актуалізація опорних знань учнів.

Для початку повторимо теоретичний матеріал. Пригадаємо основні поняття і формули послідовності та арифметичної прогресії. (Слайд 3) (Поява відповіді на слайдах після відповіді учня.)

1. Сформулюйте означення числової послідовності? Якими бувають числові послідовності?
2. Яка числова послідовність називається арифметичною прогресією? Чому дорівнює формула n-го члена АП?
3. Чому дорівнює сума n перших членів АП?
4. Задача. В арифметичній прогресії відомо 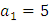, 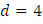. Чому дорівнює сьомий член та сума перших семи членів арифметичної прогресії?

Так само, як при вивченні питання про формулу n-го члена арифметичної прогресії, роботу на цьому етапі уроку організуємо як колективний пошук розв'язання задачі: як найраціональнішим способом знайти значення n-го члена геометричної прогресії, зна­ючи її перший член і знаменник.

ІІІ. Виклад матеріалу.

Геометрична прогресія – послідовність, кожний член якої, починаючи з другого, дорівнює попередньому члену, помноженому на одне й те саме число. Це число q – знаменник ГП. (Слайд 4)

Перший член прогресії позначають , другий , а знаменник – q (будь-яке число, крім 0). Іншими словами ГП – послідовність, що можна задати рекурентною формулою:

- задані числа

Приклади геометричних прогресій:

1. 3, 6, 12, 24, 48, 96… (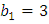, q=2);
2. 1, –3, 9, –27, 81, –243,… (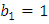, q= –3);
3. 7, 7, 7, 7, 7, 7… (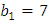, q=1)

Зауваження! Кожну арифметичну прогресію з різницею 0 можна також вважати геометричною прогресією із знаменником q=1.

– формула n-го члена геометричної прогресії.

Приклад 1. (Слайд 5) У геометричній прогресії , . Знайдіть – ?

Розв’язання: , маємо, що n=10, то 2560.

А зараз розглянемо приклад прогресії, що застосовуються в різних галузях: «Прогресії в біології», «Прогресії в фізиці». (Слайд 6)

ІV. Розв’язування вправ.

№ 18.1 (усно).

№ 18.2; 18.4 (1,3); 18.6; 18.8

V. Підсумок уроку.

Отже, на сьогоднішньому уроці ми узагальнили і систематизували знання з теми «Арифметична та геометрична прогресії», закріпили навички обчислення формул n-го члена арифметичної прогресій.  Показали їх практичне застосування в різних галузях.

Запитання до класу:

1. Що нового дізнались на уроці?
2. Що таке ГП? Чому дорівнює формула n-го члена ГП?

На цьому наш урок закінчено, спасибі вам за співпрацю.

VI. Домашнє завдання.

Розділ 3.§ 18. № 18.3; 18.5; 18.7. (Слайд 7)