Конспект уроку для 6 класу з математики на тему: «Координатна площина. Знаходження координати точки»

НКВ «ЗНЗ І-ІІ ст.. – ДНЗ» с. Мощене

Конспект уроку для 6 класу з математики на тему: «Координатна площина. Знаходження координати точки»

Підготував вчитель математики: Білоус І.В.

Тема: Координатна площина. Знаходження координат точки.

Мета:

• навчальна – сформувати поняття прямокутної системи координат, навчити знаходити координати точок;
• розвиваюча – навчити самостійно приймати рішення, та розвинути увагу;
• виховна – розвинути вміння спостерігати і аналізувати побачене.

Основні поняття: координатна площина, координатні осі, початок координат, координати точки, прямокутна система координат.

Обладнання: підручник, проектор, комп’ютер та програмне забезпечення.

Тип уроку: засвоєння нових знань і вмінь.

Хід уроку

І. Організаційний етап

Привітання та перевірка присутніх на уроці.

ІІ. Актуалізація опорних знань.

Перевірка виконаного домашнього завдання у зошиті.

Фронтальне опитування:

1. Які прямі називаються перпендикулярними?
2. Як позначаються перпендикулярні прямі в записах?
3. Які прямі називаються паралельними?
4. Як записати, що дані прямі паралельні?
5. Як побудувати пряму, паралельну даній прямій?

ІІІ. Засвоєння нового матеріалу.

Давайте з вами пригадаємо, що таке координатна пряма та які її основні елементи. (відповіді учнів)

Оголошення теми та мети уроку.

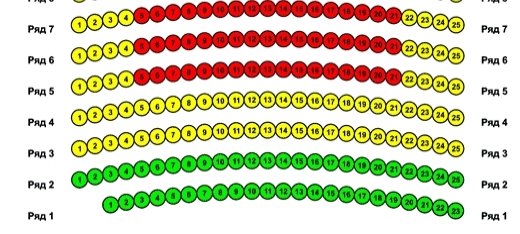
Давайте з вами уявимо, що  ми прийшли в кінотеатр і нам потрібно знайти місця, які вказані у нашому квитку. Як це зробити? Для початку вам потрібно знайти ряд, який вказаний у квитку, а потім потрібне місця. Для цього можна використати дві координатні прямі, одна буде вказувати ряд, а інша – місця. Ці прямі будуть розташовані перпендикулярно одна до одної.

І якщо ваше місце: ряд 3, місце 14. То по вертикальній координатній прямі спочатку знаходимо потрібний нам третій ряд, а потім по горизонтальній – потрібне 14 місце. Причому порядок «координат» у такій парі є строго визначений.

З цього можна зробити висновок: для того щоб знайти розміщення точки на площині, потрібно задати дві координатні прямі з рівними одиничними відрізками, які розташовані перпендикулярно одна до одної. Така пара координатних прямих утворює прямокутну систему координат.

Прямокутною системою координат називають дві взаємно перпендикулярні координатні прямі, що перетинаються в початку відліку – точці О. При цьому прямі називаються координатними осями, а точка О – початком координат.

Горизонтальна вісь називається вісь абсцис, а вертикальна – вісь ординат.

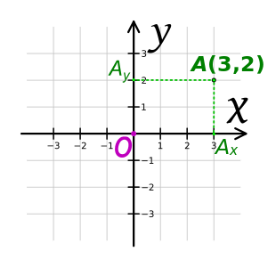Кожній точці на площині можна поставити у відповідність пару чисел у відповідному порядку. Ці числа називаються координатами точки. Координату на вісі абсцис називають абсцисою точки, а на вісі ординат – ординатою точки.

Наприклад: точка А з координатами 3 та 2 коротко записується А(3,2). Де спочатку вказуються абсциса точка, а потім ордината.

Координатні осі розбивають площину на чотири частини, їх називають координатними чвертями, які позначаються римськими числами.

Наприклад точка Р (3,5) знаходиться у І чверті.

IV Закріплення нового матеріалу

Виконання усних вправ №1523, №1524, №1526 на ст..267.

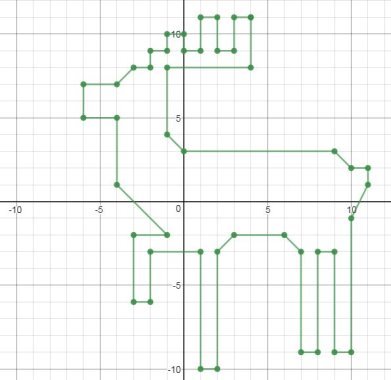
Давайте ми з вами побудуємо в Desmos точки за їх координатами та з’єднаємо послідовно їх відрізками.

(4; 11), (3; 11), (3; 9), (2; 9), (2; 11), (1; 11), (1; 9), (0; 9), (0; 10), (-1; 10), (-1; 9), (-2; 9), (-2; 8), (-3; 8), (-4; 7), (-6; 7), (-6; 5), (-4; 5), (-4; 1), (-1; -2), (-3; -2), (-3;   -6), (-2; -6), (-2; -3), (1; -3), (1; -10), (2; -10), (2; -3), (3; -2), (6; -2), (7; -3), (7; -9), (8; -9), (8; -3), (9; -3), (9; -9), (10; -9), (10; -1), (11; 1), (11; 2), (10; 2), (9; 3), (0; 3), (-1; 4), (-1; 8), (4; 8), (4; 11)

https://www.desmos.com/calculator/4o9eyufsi5

Виконати письмово №1529, №1531, №1532 на сторінці 267.

V Підбиття підсумків уроку.

Потрібно повторити з учнями, що називається прямокутною системою координат, як вона будується, як визначати координати точки в прямокутній системі координат.

VI Домашнє завдання

Письмово виконати №1533, №1535 на ст..267.

За допомогою програма Desmos побудувати та з’єднати між собою точки:

(2; 6), (-2; 10), (-2; 8), (-4; 10), (-4; 8), (-6; 6), (-8; 6), (-8; 4), (-4; 4), (0; 0), (0; 6), (2; -6), (2; 0), (6; 0), (10; -2), (10; -6), (12; -6), (12; 2), (16; 2), (12; 4), (2; 6).

Література

1. Тарасенко Н.А.. Математика 6 клас/ Н.А. Тарасенко, І.М. Богатирьова. – К.: Видавничий дім «Основа», 2014