Урок 1. Коло. Довжина кола.

Тема: Коло. Довжина кола

Мета уроку. Сформувати в учнів поняття кола, радіуса, діаметра, дуги кола, домогтися розуміння змісту залежності між радіусом кола та його довжиною, засвоєння формул для знаходження довжини кола; формувати вміння виконувати побудову кіл за допомогою циркуля; розвивати вміння працювати з підручником, виокремлювати головне; сприяти розвитку уваги; виховувати самостійність, дисциплінованість.

Обладнання та наочність. Підручник, роздатковий матеріал.

Тип уроку.  Засвоєння нових знань.

Методи і прийоми навчання. Зразковий стіл, практична робота, робота в парах.

 

 I. Організаційний етап

Привітання

Прийом

«Зразковий стіл»

Перед початком уроку оголошується конкурс серед учнів, які сидять за партою, на кращу підготовку навчального приладдя та навчальних посібників до уроку. На початку уроку за результатами конкурсу огололошується «Зразковий стіл»(їх може бути декілька)

 

 II. Перевірка домашнього завдання

Самостійна робота

 Знайдіть число, відсоток від якого становить 3,5 м. Заповніть таблицю.

 

								■"+•
	Якщо 3,5 м ста­новить:	1%	2%	4%	5%	10%	20%	25%	50%	100%	150%
	число дорівнює:	350 м

1.                    Передноворічна знижка на мікрохвильову піч, вартістю 960 грн, стано­вила 25 %. За скільки можна було купити мікрохвильову піч напере­додні новорічних свят?
2. Ціна на портативний телевізор зменшилась на 10 %, згодом — ще на

10 % і стала 243 грн. Якою була початкова ціна цього телевізора?

3.  Електроплитка коштувала 700 грн. Магазин провів уцінку товарів і зменшив ціну на 10 %. Згодом її було збільшено на 20 %. Яка тепер ціна електроплитки?

III. Актуалізація опорних знань, мотивація навчальної діяльності.

Математика - наука древня, цікава і корисна. Сьогодні ми з вами у черговий раз переконаємося в цьому, і дуже хочеться, щоб кожен з вас для себе зробив хоч би невелике, але відкриття. А як сказав великий учений, математик Лейбніц: "Хто хоче обмежитися сьогоденням, без знання минулого, той його ніколи не зрозуміє"., Тому і  нам з вами для успішної роботи треба повторити деякі геометричні фігури і поняття, згадати правила для округлення десяткових дробів до різних розрядів, виконання множення і ділення десяткових дробів і знаходження невідомих компонентів в діленні і множенні.

- Сформулюйте правило для множення десяткових дробів.

- Сформулюйте правило для округлення десяткових дробів.

- Давайте згадаємо, з якими геометричними фігурами ми знайомі?

- Яка фігура зображена? (проектуються зображення прямокутника, квадрата , трикутників, кола, круга)

- Що можна за допомогою лінійки виміряти? Знаючи сторони, що можемо знайти? Назвіть формулу для знаходження периметра. Знайти периметр.

- Що це за фігура і т. д.

- Де в житті ми зустрічаємося з формами, що дають уявлення про коло,круг?

- А можемо ми виміряти, наприклад, довжину бордюру круглої клумби або довжину границі  циркової арени?

- Як? (За допомогою мотузка, нитки, потім розпрямити і виміряти лінійкою)

Отже , діти, сьогодні на уроці наше завдання знайти універсальний спосіб для знаходження довжини кола, познайомитися з одним дивовижним числом і застосувати наш спосіб для вирішення практичних завдань.

 Оголошується тема уроку

ІV. Вивчення нового матеріалу

Дається поняття і вводиться позначення  діаметра і радіуса кола.

Вводиться позначення довжини кола.

 Як ви думаєте, в яких одиницях, вона вимірюється?

- Який зв'язок між діаметром і радіусом?

• Як побудувати коло за допомогою циркуля?
• Яка точка є центром кола?
• . Що називають дугою кола?
•  Скільки радіусів, діаметрів можна провести в колі?
•  Що називають хордою кола?

 Практична робота

Діти, ще в далекому минулому було встановлено, що також є залежність між довжиною кола і її діаметром.

Давайте ж і ми спробуємо її встановити, для цього ви виконаєте практичну роботу, в якій використовуватимете спосіб виміру довжини кола, запропонований вами, але для зручності користуватиметеся  ниточкою.

У вас на столах лежать різні круги і як ви говорили, що межа круга - це коло, то довжини кіл, що їх обмежують різні.

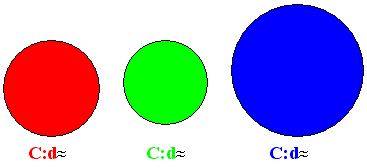
1. Проведете діаметр  кожного кола і виміряйте   його

2. За допомогою  нитки вимірюємо довжину  кожного кола

3. Як ви думаєте, чия довжина більша? А як визначити в скільки разів?

Розділіть довжину кола на діаметр і результат округлите до цілих.

Для отримання найбільш точних результатів, працюйте в парах.

Після виконання роботи, зробіть висновок: приблизно в скільки ж раз довжина кола більше свого діаметру.

Індивідуальне завдання дається одному учневі: розділити довжину кола на її діаметр, якщо С=22м, d=7м.

 

Для кожного кола більшість з вас отримали, що її довжина приблизно в 3 рази більше її діаметра.

Зараз ми з вами дійшли такого ж висновку, що і наші далекі предки багато віків тому. Вони помітили, що для того, щоб сплести кошик потрібної ширини,  треба було брати лозини приблизно в три рази довші. Це було перше відкриття, відтоді пройшло немало віків, перш ніж учені довели, що результат ділення довжини кола на її діаметр постійний і виражається не натуральним числом. А яким же?

Якщо ви, діти , округлили ваш результат, то ваш товариш, виконував наступне завдання: спробував виконати ділення С=22 на d=7 до кінця. І що ж у тебе вийшло, учень записує свій результат. Так, дійсно, виходить нескінченний десятковий дріб. Такого висновку дійшов старогрецький вчений Архімед. 

У 1706 році англійський математик Уільямс Джонс для нього ввів спеціальне позначення це  перша буква слова "периферія", в перекладі з грецького "коло". Незвичність і дивовижність цього числа в тому, що його можна обчислювати нескінченно і у нього буде нескінченне число знаків після коми. Це, проте, не утримує математиків від спроб обчислити якомога більше десяткових знаків числа пі. Про нього говорять, як про невловиме число.

Використовуючи свої  висновки учені, отримали, що для будь-якого кола С:d=π І тепер ми можемо отримати формулу для знаходження довжини кола - це якраз і є універсальний спосіб.

Давайте виразимо звідси С . Чим воно є?

Отримаємо С=πd . Підставивши в цю формулу замість d =2r отримаємо С=2πr. для того, щоб знайти довжину кола треба знати її діаметр або радіус, а можна навпаки, знаючи довжину кола знайти діаметр, а як?

 

 VI. Закріплення вивченого матеріалу

▪ Виконання усних вправ

1. Знайдіть довжину кола діаметром 20 см .

2. Дано коло радіусом 14 мм. Назвіть довжину діаметра кола.

▪ Робота учнів біля дошки і в зошитах

Впр. 757(виконують в зошитах здійснюючи взаємоперевірку), 

763(робота з підручником),   759, 761, (усно)

765(коментовано в зшитах)

771(виконують самостійно в зошитах з наступною вибірковою перевіркою вчителем)

Впр 776

Розв'язання

С=3,14·1,6=5,024(м) – довжина обводу колеса

5,024·300=1507,2(м)=1,5072(км)- шлях колеса

1,5072:0,025=60,288=60,3(км/год) – швидкість тепловоза

 

 VII. Підбиття підсумків уроку

 Фронтальне опитування

1. Як розміщені точки кола відносно його центра?

2. Що називають радіусом кола?

3. Що називають хордою кола?

4. Що називають діаметром кола?

5. Який зв’язок між діаметром і радіусом одного кола?

 

 VIII. Домашнє завдання

Вивч. § 29

Впр.  760 (1,2),763 (І-ІІ р.)

Впр. 773, 776 (ІІІ-ІVр.)

Впр. 777

Розв'язання

С=3,14·0,9=2,826(м) – довжина обводу колеса

2,826·7=19.782=0.019782(км)- шлях, який проїде автомобіль

0.019782:0,0003=65.99км/год)