Конспект уроку "Координати середини відрізка"

Тема уроку: Координати середини відрізка.

Мета уроку: вивести формулу для знаходження координат середини відрізка; навчити учнів застосовувати дану формулу до розв’язування задач; розвивати увагу, логічне мислення, виховувати акуратність математичних записів.

Хід уроку

І. Організаційний  етап.

ІІ. Перевірка домашнього завдання. 

• Дати відповіді на питання, які виникли під час виконання домашнього завдання.
• Один учень виконує на дошці завдання, аналогічне домашньому завданню (самостійно, з подальшим поясненням).

Задача. Вершинами трикутника є точки А(-1;3), В(5;9), С(6;2). Доведіть, що трикутник АВС –рівнобедрений.

Розв’язання:

АВ=;

ВС=;

АС=.

ІІІ. Актуалізація опорних знань.

Вправа «Мікрофон»

• Що називають прямокутною системою координат?
• Як називається горизонтальна вісь?
• Як називається вертикальна вісь?
• Як записати координати будь-якої точки на координатній площині?
• Як називають першу координату?
• Як називають другу координату?
• Які знаки мають координати точок в кожній із координатних четвертей?

Слайд  2

1. В якій четверті знаходиться точка: А(1;2),  В(-1;-4),  К(2;-5),  М(-2;3),  Р(3;4),  D(-5;1),  F(3;-2),  С(-2;-1)?
2. Де знаходяться точки: Х(0;-3),  У(-1;0),  N(0;5),  O(0;0),   Q(4;0)?

• Як знайти відстань між двома точками координатної площини? (записати формулу на дошці).

Слайд 3 (для перевірки формули).

Слайд 4.

Задача. Знайти відстань між точками А(1;3) і В(4;7).

Розв’язання:  АВ= = 5.

ІV. Повідомлення теми і завдань уроку. Слайд 5.

V. Сприймання та усвідомлення нового матеріалу.

Нехай відрізок АВ має кінці А(х₁;у₁) і В(х₂;у₂) і нехай М(х₀;у₀) – середина відрізка АВ(див. рис.1), тоді MD – середня лінія трапеції з основами х₁ і х₂, МС – середня лінія трапеції з основами у₁ і у₂.

     у

    у₂                                      В

    у₀                        М

    у₁            А

    0          х₁         х₀          х₂              х

                             ^Рис.1

За властивістю середньої лінії трапеції  маємо:

                                             ;         .      Слайд 6.

Ці формули дозволяють за координатами кінців відрізка знаходити координати середини відрізка, а також за координатами середини й одного із кінців відрізка знаходити координати другого кінця.

Слайд 7 (для прикладу)

Задача. Знайдіть координати середини відрізка ВС, якщо В(5;4),  С(3;2).

Розв’язання:

х= = = 4;

у= = = =3.

т. О(4;3) – середина відрізка ВС.

VІ. Осмислення нового матеріалу.

1. Робота в парах на картках. Слайд 8.

Картка №1. Знайдіть координати середини відрізка з кінцями в точках  А(-1;1) і В(5;-5).

х= ;

у= .                 (2;-2)

Картка №2. Знайдіть координати середини відрізка з кінцями в точках  М(6;4) і N(2;-2).

х= ;

у= .                      (4;1)

Картка №3. Знайдіть координати середини відрізка з кінцями в точках  K(1;4) і L(9;-6).

х= ;

у= .                (5;-1)

2. Задача. Слайд 10.

Знайдіть координати кінця діаметра, якщо другим його кінцем є точка

 (-5;2), а центром кола – точка (2;0).

                                             Розв’язання:

                                               х=;   2=;   ;  

                            В(5;-2)

                           О(2;0)                       у= ;  0= ;  ;  .

  А(х₁;у₁)

Відповідь: А(-1;2).

3. Робота з підручником. Слайд 11.

№31.

 Знайдіть довжину медіани АМ трикутника АВС, якщо А(5;1), В(-3;-2), С(-5;-6).

                     В(-3;-2)

                            М(х;у)

        А(5;1)                                С(-5;-6)

1. Що таке медіана?
2. За якою формулою ми можемо знайти довжину медіани, тобто довжину відрізка АМ?
3. Як знайти координати точки М?

4. Самостійне розв’язування задачі. Слайд 12.

Задача. Дано точки А(0;3), В(3;8), С(5;4). Знайдіть координати кінців середньої  лінії трикутника АВС, паралельної стороні АС.

1. Що таке середня лінія трикутника?
2. Знайдемо координати середини сторони АВ (нехай точка К).
3. Знайдемо координати середини сторони ВС (нехай точка Р).

VІІ. Підсумок уроку.

1. Чи правильно записано формули  координат середини відрізка з кінцями у точках А(х₁;у₁) і В(х₂;у₂)? Слайд 13.

1. ; .
2. ; .
3. ; .

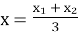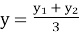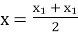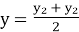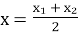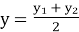2. Дано три точки А(-1;3), В(3;6), К(1;5). Чи є точка К серединою відрізка АВ? Слайд 14.

VІІІ. Домашнє завдання. Слайд 15.

Опрацювати  §1 (п.4), розв’язати №30, №33.

ІХ. Оцінювання учнів.