Конспект уроку "Квадрат"

Мета уроку: дати означення квадрата;

навчальна: розглянути його властивості, спираючись на відомі учням властивості вивчених видів паралелограма; розглянути задачі на застосування властивостей квадрата;

розвивальна: розвинути у дітей навички для розв’язування задач, логіку і мислення;

виховна: виховати почуття відповідальності і самостійності.

Тип уроку: засвоєння нових знань.

Обладнання: таблиця «Квадрат».

Хід уроку

І. Організаційний момент

ІІ. Перевірка домашнього завдання

З місця за готовим рисунком один з учнів пояснює розв’язання задачі середнього рівня. Інший учень пише на дошці розв’язання задачі достатнього рівня. Також після опрацювання нової теми дам самостійну роботу для закріплення тем паралелограм, прямокутник і квадрат.

Задача №121 (а) Знайдіть кути ромба, якщо висота, проведена з вершини тупого кута, відтинає від ромба рівнобедрений трикутник.

Розв’язання

Так як висота відтинає від ромба рівнобедрений трикутник і утворює зі стороною прямий кут, то інші два кути будуть мати по 45°,  тобто гострий кут ромба буде дорівнювати 45°. А отже, гострий кут дорівнюватиме 135°.

Відповідь: 45°, 120°, 45°, 120°.

Самостійна робота (додаток 1)

ІІІ. Формулювання теми, мети і завдань уроку

IV. Актуалізація опорних знань учнів

Пропоную учням самостійно накреслити квадрат.

Запитання до класу:

1.              Як ще можна назвати цю фігуру? (Чотирикутник, прямокутник, паралелограм, ромб.)
2.              Як можна різними способами визначити цю геометричну фігуру? (Це паралелограм, у якого всі кути прямі і всі сторони рівні. Це чотирикутник, у якого всі сторони і кути рівні. Це прямокутник зі всіма однаковими сторонами. Це ромб, у якого всі кути прямі.)

V. Вивчення нового матеріалу

Учитель звертає увагу на правильність усіх даних означень і пропонує виходячи з них назвати ознаки і властивості квадрата та самостійно скласти таблицю «Квадрат».

Квадрат

VI. Формування умінь

Розв’язування задач

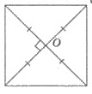
Задача № 113. Периметр квадрата дорівнює 40 м. Знайдіть відстань від точки перетину діагоналей квадрата до його сторони.

Розв’язання:

Нехай АВСD – квадрат, АС,BD -  діагоналі, що перетинаються в точці О; КО – відстань від точки перетину до сторони квадрата. Якщо Р=40 і з властивості квадрата всі сторони рівні, то сторона дорівнює 10 м. Показати, що КО дорівнює половині сторони квадрата, і дорівнює 5м.

Відповідь: 5 м.

Задача №123. Діагональ квадрата дорівнює 18 см, а його сторона є діагоналлю іншого квадрата. Знайдіть периметр другого квадрата.

Розв’язання:

Нехай дано квадрат АВСD i KBMA. AM – сторона квадрата KBMA, АС – діагональ квадрата АВСD і дорівнює 18 см і АМ дорівнює половині АС, тобто АМ=9  см. Так як це квадрат, то всі сторони рівні і Р=4*9=36 (см).

Відповідь: 36 см.

VII. Підбиття підсумків уроку

На цьому уроці ми ознайомилися з останнім видом чотирикутника – квадратом, який має всі вивчені раніше властивості паралелограма. Учні ще раз формулюють ці властивості.

VIII. Домашнє завдання

Повторити усі види чотирикутника, їх властивості і ознаки. Для закріплення пройденого матеріалу виконати домашню контрольну роботу. Задача 1. У ромбі АВСК бісектриса кута АВК проходить через середину сторони АК. Знайдіть кути ромба. (Відповідь: 60°, 120°, 60°, 120°.)

Задача 2. З вершини одного з кутів паралелограма проведені бісектриса цього кута і висота. Кут між ними дорівнює 30°. Знайдіть кути паралелограма. (Відповідь: 60°, 120°, 60°, 120°.)

Задача 3. У прямокутнику ВСКМ бісектриса кута В утворює з діагоналлю ВК кут 20°. Знайдіть кути між діагоналями прямокутника.