Конспект уроку на тему "Перпендикуляр і похила, їх властивості."

МІ-42          Богдан Юлія

Урок №38        Дата ___________

Тема: Перпендикуляр і похила, їх властивості.

Мета:

Навчальна: ознайомити дітей з поняттям перпендикуляра і похилої, навчити  виконувати побудову перпендикуляра і похилої, розв’язувати задачі на застосування даних відрізків, задачі практичного характеру;

Розвивальна: сприяти розвитку інформаційно-комунікативної то природничо технологічної компетентностей, пам’яті, уваги, уяви;

виховувати почуття відповідальності, інтерес до предмета, уміння організовувати свою роботу та розраховувати час.

Обладнання: Підручник з математики 8 клас (Істер), Збірник задач і контрольних робіт з алгебри 8 клас (Мерзляк).

Хід уроку

1. Організаційний етап

• Привітання
• Перевірка присутності учнів на уроці
• Перевірка готовності учнів та кабінету до уроку

2. Перевірка домашнього завдання

Чи були у вас проблеми при виконанні завдань? Якщо так, то один з учнів хто виконав це завдання пояснює його біля дошки. Якщо ні, то просто перевіряю наявність домашньої роботи у зошитах.

Самостійна робота: за посиланням: https://learningapps.org/watch?v=pqqggisaj19

Або QR кодом

3. Актуалізація опорних знань

1. Що таке трикутник?
2. Який трикутник називають прямокутним?
3. Намалюйте прямокутний трикутник ABC та вкажіть усі його елементи.
4. Які прямі називають перпендикулярними?
5. Що таке перпендикуляр?

4. Засвоєння нових знань

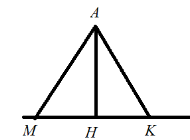
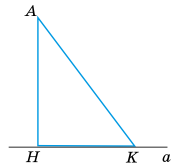Розглянемо трикутник AHK: кут AHK – прямий, пряма а містить катет НК.

АН – перпендикуляр проведений з т. А до прямої а.
т. Н – основа перпендикуляра
Нехай т. К – довільна точка з прямої а, відмінна від т. Н, тоді
АК – похила
т. К – основа похилої
НК – проекція похилої АК на пряму а.

Розглянемо властивості перпендикуляра та похилої:

Властивість 1. Перпендикуляр, проведений з точки до прямої, менший від будь-якої похилої, проведеної із цієї точки до прямої.

□ Розглянемо трикутник AHK: кут AHK – прямий, АН – катет (перпендикуляр), АК- гіпотенуза (проекція). Тому АН<АК. ■

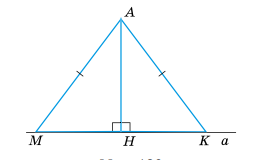Властивість 2. Якщо дві похилі, проведені з точки до прямої, між собою рівні, то рівні між собою і їх проекції.

□ Нехай з т. А до прямої а проведено 2 похилі АК і АМ (АК=АМ) і перпендикуляр АН. Тоді АНК=АНМ (за катетом та гіпотенузою), а тому НК=НМ. ■

Властивість 3. Якщо проекції 2 похилих проведених з точки до прямої, між собою рівні, то рівні між собою і самі похилі.

□ Нехай з т. А до прямої а проведено 2 похилі АК і АМ і перпендикуляр АН. Тоді НМ і НК є проекціями, при чому НК=НМ, з цього АНК=АНМ (за 2 катетами), а тому АК=АМ. ■

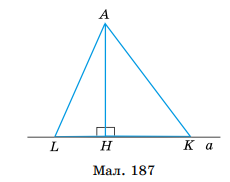Властивість 4. З 2 похилих, проведених з точки до прямої, більшою є та, у якої більша проекція.

□ Нехай АК і AL – похилі, НК>HL.

Тоді АК²=АН²+НК²

 АL²=АН²+НL²

Але НК>HL, тому АК²> АL², отже АК> АL. ■

Властивість 5. З 2 похилих, проведених з точки до прямої, більша похила має більшу проекцію.

□ Нехай АК і AL – похилі, АК> АL.

Тоді НК²=АК²-АН²

 НL²=АL²-АН²

Але АК> АL, тому НК²> НL², отже НК>НL. ■

Де ж в житі використовують перпендикуляр, похилу та їх властивості? (На дошці розмістити роздруковані картинки)

Приклад 1.

Методичний коментар. Для того щоб дати відповідь на запитання задачі слід використати теорему Піфагора для трикутника AHL та властивість катета, шо лежить навпроти кута 30^О для трикутника АНК.

Приклад 2.

Методичний коментар. Для того щоб дати відповідь на запитання задачі слід використати властивість 4 перпендикуляра та похилої та теорему Піфагора.

5. Вправи для закріплення

Індивідуальна робота біля дошки. Учні по черзі виходять до дошки та виконують з детальним коментуванням запропоновані завдання. (К. – володіння державною та рідною мовою)

№ 686 (Істер)

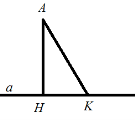Дано: АН – перпендикуляр до а, АН=5 см, АК – похила, АК=13 см.

Знайти: НК

Розв'язання

Розглянемо трикутник АНК (Н=90^О)

Методичний коментар: для того щоб дати відповідь на запитання задачі слід розглянути прямокутний трикутник, що утворився та за допомогою теореми Піфагора знайти невідомий катет який і буде шуканою проекцією.

№ 688 (Істер)

Дано: АМ, АК – похилі, АМ=АК, НМ, НК – проекції,

НМ=6 см.

Знайти: МК

Розв’язання

За властивістю 2 маємо, що НМ=НК=6 см. Так як проекції лежать на одній прямій, то МК=НМ+НК=6+6=12(см).

Методичний коментар: для того щоб дати відповідь на запитання задачі слід застосувати 2 властивість перпендикуляра та похилої.

№ 692 (Істер)

Дано: АМ, АК – похилі, АМ=13 см, НМ – проекція АМ, НМ=5 см, АКН=45^О

Знайти: НК

Розв’язання

Розглянемо АНМ (АНМ=90^О)

.

Розглянемо АНК (АНК=90^О) Якщо АКН=45^О, то НАК=90^О-АКН=90^О-45^О=45^О. Отже АНК – рівнобедрений, з цього АН=НК=12 см.

Методичний коментар: для того щоб дати відповідь на запитання задачі слід розглянути 2 прямокутних трикутники. В 1 використати теорему Піфагора та знайти невідомий катет (перпендикуляр), в другому застосувати ознаку рівнобедреного трикутника та знайти НК.

№ 178 (Мерзляк)

Господар для збереження свого врожаю вирішив підв’язати огірки. Для цього він використовував дерев’яний кіл, до якого підв’язував один кінець нитки, а інший відтягував до ямки з насінням, для того, щоб коли проросте, змогло витися по даній тинці. В результаті від одного кола відходили нитки до двох ямок. Оскільки кіл був розміщений не по центру, то довжина ниток до ямок була різною. До однієї ямки вона становила 30 см, до іншої 26 см. Висота самого кола становила 24см. Чому дорівнює різниця відстаней від ямок до кола?

Розв’язання

Створимо геометричну модель даної ситуації.

АН – кіл (перпендикуляр)
АМ, АК – натягнуті нитки (похилі)

НМ, НК – відстані від ямок до колу (проекції)

Дано: АМ=30 см, АК=26 см, АН=24 см

Знайти: МН-НК

Розв’язання

Розглянемо АНМ (АНМ=90^О)

.

Розглянемо АНК (АНК=90^О)

МН-НК=18-10=8(см).

Методичний коментар: для того щоб дати відповідь на запитання задачі слід створити математичну модель даної ситуації

6. Підбиття підсумків уроку

• Що нового ви дізналися сьогодні на уроці?
• Що було для вас уже відомим?
• Що було цікавим на уроці?
• Над чим ще варто попрацювати?

7. Домашнє завдання

§ 19 № 687, 689.