Конспект уроку "Логарифмічні рівняння "
Конспект уроку ознайомлення учнів з новим матеріалом та його первісного закріплення за підручниками Алгебри і
початків аналізу (профільний рівень) Мерзляк А.Г., Номіровський Д.А., Полонський В.Б., Якір М.С., Логарифмічні рівняння (11 клас)
Тема: Параграф №1 Тема №6 «Логарифмічні рівняння. Методи
розв’язування логарифмічних рівнянь» (стр. 48-61)
Мета: сформувати поняття логарифмічного рівняння і розглянути методи розв’язання логарифмічних рівнянь. Розвивати логічне мислення через встановлення причинно-наслідкових зв’язків, вчити учнів лаконічно і точно висловлювати свою думку, узагальнювати, обґрунтовувати, виділяти головне.
Тип уроку: урок засвоєння знань.
Обладнання: ІКТ.
Хід уроку
I. Організаційний етап. Перевірка готовності учнів до уроку.
II. Актуалізація знань учнів. Фронтальна форма роботи.
1) Дати визначення логарифма.
2) Основна логарифмічна тотожність.
3) Властивості логарифмів.
4) Область визначення логарифмічної функції.
Розв’язування рівнянь:
Поясніть, у чому полягає метод розв’язання:
a) Лінійних рівнянь;
b) Квадратних рівнянь;
c) Графічного методу розв’язання рівнянь.
III. Мотивація навчальної діяльності учнів. Вчитель пропонує розглянути «асоціативний кущ», який проектується на екран.
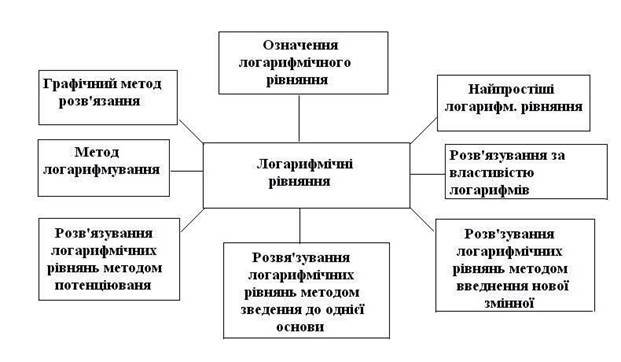
IV. Оголошення теми і мети уроку.
V. Засвоєння поняття «логарифмічне рівняння» та «методи їх розв’язання».
При поясненні нового матеріалу використовую технологію розвивального навчання, а саме – метод евристичної бесіди та проблемні ситуації.
1) Означення логарифмічного рівняння.
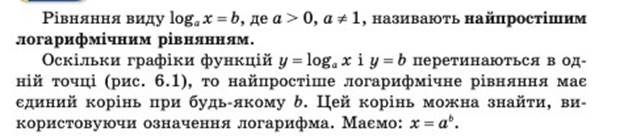
|
Приклади. |
|
|
|
logx = 1+lg2x |
√logx = lg √x |
log2(x+3) = 4 |
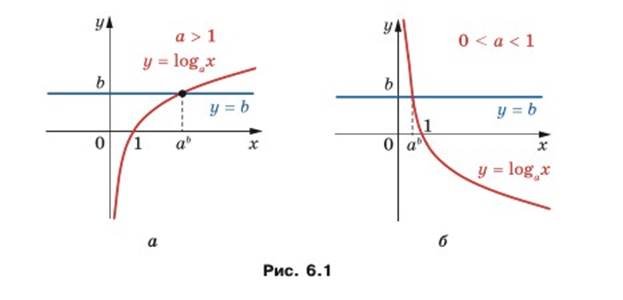
2) Найпростіші логарифмічні рівняння: 1) logax = b, де a>0, a≠1, x>0. За означенням логарифма x=ab.
2) logax = logab, a>0, a≠1, b>0, x>0. x=b
3) logxa = b, x>0, x≠1, a>0 xb=a, x=a1/b
3) log3(2x+1) = 2 ОДЗ: 2x+1>0
x> -1/2
2x+1=32 2x=8 x=4
Відповідь: 4.

При розгляданні методів розв’язування логарифмічних рівнянь звертається увага на знаходження ОДЗ, або обов’язкової перевірки коренів рівняння.
Розв’язування логарифмічних рівнянь за властивостями логарифмів. log2(x-3) + log2(x-1) = 3 + log2(x-4)
1. Введення нової змінної.
(lgx – 6)-1 + 5(lgx + 2)-1 = 1
2. Графічний метод.
lgx = 1 – x
3. Метод логарифмування. x log2x = 16
4. Метод потенціювання.
log5(x - 1) + log5(x - 2) = log5(x - 2)
5. Метод зведення до однієї і тієї ж основи.
log3x – 2log1/3x = 2
VI. Набуття умінь розв’язувати логарифмічні рівняння.
1) Усне розв’язування логарифмічних рівнянь.
log5x = 2 log9x =?
2log2x = 4 lg(x+3) = lgx lg(5-x)= -1 lgx+12 = 1 lgSinx=0
2) Виконуємо разом. №6.1 (1, 6), №6.3 (1), №6.5 (1,6), №6.17 (5,6).
3) Самостійна робота з послідовною взаємоперевіркою. №6.10 (1), №6.12 (2), №6.20 (2).
VII. Підсумок уроку.
Встановити відповідність між заданими рівняннями та їх коренями.
|
Рівняння |
|
Корені |
|
1) log2(x2-1)=3 |
А) x=1/49 |
|
|
2) log4(x+1)=2 |
Б) x±3 |
|
|
3) log7x= -2 |
В) x=2 |
|
|
4) log2(x-1)=0 |
Г) x=15 |
|
VIII. Домашнє завдання.
§6. №6.22 , №6.29 (2,3), №6.34 (1,2), №6.40 (1), 6.43.


про публікацію авторської розробки
Додати розробку
