Конспект уроку математики у 6 класу на тему: Додавання від'ємних чисел

Дата  ____________ № уроку _________        Математика 6 клас

 

Тема уроку:  Додавання від'ємних чисел

Мета тематичного дня: вивчити правило додавання від’ємних чисел та навчитися

застосовувати його до розв’язування вправ, задач; розвивати логічне мислення і обчислювальні навички; формувати культуру математичних записів та мови; виховувати позитивне ставлення до навчання, упевненість в своїх силах.

Предметні компетентності:

-Математичну компетентність шляхом розвитку цікавості учнів до математики, логічного мислення, зорової  пам’яті, свідомого сприйняття матеріалу; розв’язування математичних завдань, зокрема практичного змісту; вивчення та застосування лічби;

-Компетентність спілкування державною мовою для розуміння, пояснювання і перетворення математичних текстів; використання математичних термінів на початковому рівні;

-Загальнокультурну компетентність для бажання більше дізнатися про математичні знання в різних життєвих ситуаціях.

Обладнання: підручники, папір А4, ручки, набори «Лего», ілюстративний та

роздатковий матеріал, мультимедійна презентація.

Тип уроку: урок формування компетентностей.

 

Зміст заняття:

І. Етап орієнтації. Мотивації діяльності

Вправа «Числовий настрій»

Обери цифру настрій, якої відповідає твоєму.

 

 

ІІ. Етап цілепокладання

Інтелектуальна розминка.

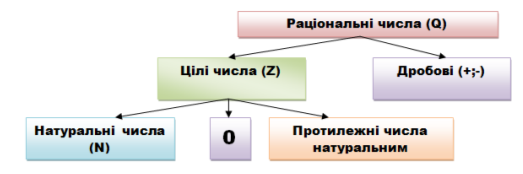
1. Які числа називаються цілими? Раціональними?
2. Як називаються числа більше нуля? А менше нуля?
3. Де використовують від’ємні числа?
4. Що називається модулем числа а ?
5. Знайти серед чисел від’ємні

7,6 ; -0,9 ; 0 ; -(-3); -(+6); -0,87 .

6.  Обчислити:

7+0,08                           0,23+7

0,48+0,2                       7+0,05+0,8

2,01+1,3+0,09              2

7. Вказати правильну рівність:

|-7| = 7 ;  |56| =-56; |-58| = 58;  |-3| = 3 ; |-8,2| = 8 ; |0| = 0;   || = 1,2.

Заповнити схему:

«Мозковий штурм»:

• Крім додатних чисел, які ще існують числа?
• Які числа називають натуральними?
• Які числа називають цілими?
• 0 – натуральна число? Ціле число? Раціональне число?
• Які числа називають раціональними?
• Які числа називають протилежними? Приклад.
• Що називають модулем числа? Чи може модуль числа бути від'ємним? Чому?
• З двох чисел на координатній прямій, яке міститься правіше?

• Додатне чи від’ємне?
• 0 чи додатне?
• 0 чи від’ємне? Чому?

Виберіть із чисел: - 3; 5; 1,9; -6; 6; 5,3; 8; 0; 3; -2; -10; 8; -7,7; - 4; 8,05.

• Натуральні;
• Додатні;
• Недодатні;
• Дробові невід'ємні.

Оголошення теми та мети уроку

 

ІІІ. Етап цілереалізації

Метод «Асоціативний кущ»

Запишіть, де використовують позначення з від’ємними числами.

Історична хвилинка

З історії від’ємних чисел:

      1. Китайці додатними числами позначали майно, свої гроші, прибуток. Додатнім числам раділи і позначали їх червоним кольором вони їх називали «чен», що означає червоний.

       Від’ємні числа не любили, їх називали «фу», що перекладається, як чорний. Ними  позначали борг, збиток, недостачу і зображали їх чорним кольором. Такий спосіб позначення чисел Китайці використовували до середини  XIII ст., поки Лі Є не запровадив зручніше позначення від’ємних чисел — цифри, що зображали від’ємні числа, перекреслювали рискою навкіс справа наліво. 

     2.  У Давній Греції дії з від’ємними числами увів Діофант у ІІІ ст. н.е. Їх широко використовували індійські математики у VI-VII ст. н.е., які розуміли додатні числа як майно, а від’ємні – як борг.

     3. Індійський  математик Бхаскарі (ХІІ ст.) склав правила дій для від’ємних і додатних чисел:

«Сума майна є майно».

«Сума двох боргів є борг».

«Сума майна і боргу дорівнює їх різниці».

«Сума майна і такого самого боргу дорівнює нулю».

       4. Цікаві аналогії правила знаків під час множення цілих чисел,  які використовували арабські математики:
Друг мого друга — мій друг,
Друг мого ворога — мій ворог,
Ворог мого друга — мій ворог,       
Ворог мого ворога -  мій друг.

          5. Довгий час від’ємних чисел не визнавали, вважали їх несправжніми, абсурдними, фіктивними. Бхаскарі так і писав: «Люди не схвалюють від’ємних чисел».

          6.  Важко входили від’ємні числа в математику. В Європі вперше про них згадує італійський математик Леонардо Пізанський (Фібоначчі, ХІІ – ХІІІ ст.). Німецький математик Михайло Штіфель (ХVІ ст.) називає від’ємні числа «меншими ніж ніщо». Він пише: «Нуль міститься між істинними і абсурдними числами».

          7. Протягом 18-ти  століть математики різних країн незалежно один від одного приходили до поняття від’ємного числа, але навіть у XVI-XVII ст. більшість європейських вчених ще не визнавали від’ємних чисел. Сучасне розуміння від’ємних чисел пов’язане з рухом ліворуч від нуля по числовій прямій, прийшло з працями французького математика і філософа Рене Декарта (1596-1650). І тільки з початку ХІХ ст. від’ємні числа стали у математиці такими ж звичайними як і додатні.

МАТЕМИАТИКА РАЗОМ З ДРУГОМ

Математичний диктант.

МАТЕМАТИКА ПИСЬМОВО

Каліграфічна хвилинка

Робота з підручником

Вам, напевне, відомі такі ігри (наприклад, доміно), у яких той, хто переміг, одержує певну кількість заохочувальних очок, а той, хто програв, — штрафних очок. Якщо, наприклад, гравець за одну гру виграв 3 очка, а за наступну 5 очок, то загальну кількість виграних очок знаходимо додаванням 3 + 5 = 8, або можна записати: (+3) + (+5) = +8. Якщо гравець за одну гру отримав 3 штрафних очка, а за наступну 5 штрафних очок, то загальну кількість штрафних очок знаходимо також додаванням. Якщо кількість штрафних очок записати від'ємними числами, то отримаємо: (-3) + (-5) = -8. Число -8, а також вираз (-3) + (-5) — це сума чисел -3 і -5.

Звернімося до підручника. Розглянемо приклад (учні розглядають приклад з підручника з коментуванням учителем незрозумілих місць).

Отже, прочитаємо правило додавання від'ємних чисел.

Щоб додати два від’ємних числа, треба:

1) знайти модулі доданків;

2) додати модулі доданків;

3) перед отриманим числом поставити знак (-).

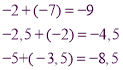Приклади:

 

 

4. Розглянемо координатну пряму.

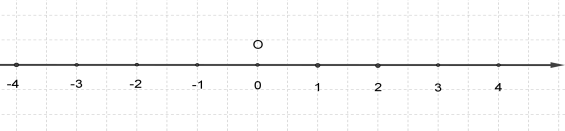
Якщо до числа a додати додатне число b, то точка з координатою a переміститься по координатній прямій на b одиничних відрізків праворуч.

Якщо до числа a додати від’ємне число b, то точка  з координатою a переміститься по координатній  прямій на  b одиничних відрізків ліворуч.

 Завдання: за допомогою координатного променя  до числа -3 додати число -9.

 -3+(-9) = -12 

http://learningapps.org/watch?v=p2raibkdj01

Фізкультхвилинка.

https://www.youtube.com/watch?v=jTWryZ8fDww

МАТЕМАТИКА САМОСТІЙНО

Робота в парах диференційовано

Рівень складності: високий

Завдання: До суми чисел -2,75 і -1 додайте число, протилежне .

Рівень складності: достатній.

Завдання: Знайти значення виразу а+в+с+ (-1204), якщо а= -756; в= -; с=-.

Рівень складності: середній.

Завдання:  Протягом першої половини дня температура змінилася на -1,5°С, а протягом другої – на -3,5ºС. На скільки градусів змінилася температура повітря протягом дня?

Самостійна робота з самоперевіркою.

1 варіант	2 варіант
1)           -10+(-7)	-12+(-5)
2)        -7,14+(- 12,4)	-4,6+(- 16,4)
3)        -15,25 + ( - 255,05)	-12,75 + (- 388,02)
4)        -2 + ( -3 )	- 3 + (- 4)
5)           -0,2+(-3)	-  2 + ( -2,5)

Інтерактивне завдання

https://learningapps.org/view9159463

МАТЕМАТИЧНІ ДОСЛІДЖЕННЯ

Фермер Дзюба у квітні взяв кредит 5 тисяч грн. у банку «Дніпро», а наступного місяця ще отримав кредит на 3 тисячі грн. Скільки коштів заборгував фермер банку «Дніпро»?

В середу вечері температура повітря була - 10°, а до ранку температура повітря знизилася ще на 8°. Визначте, яка температура повітря була на ранок.

 

ІV. Етап рефлексійно-оцінюючий

Рефлексія

— Чого навчилися на уроці?

• З чим виникли проблеми? Що ви не зрозуміли?
• Чи спободався вам урок?

— Оцініть свою роботу.

 

 

Список використаних джерел

1. Леонова Валентина. Презентація Додатні та від’ємні числа. Режим доступу https://naurok.com.ua/dodatni-ta-vid-emni-chisla-283694.html
2. Історія виникнення від’ємних чисел. Режим доступу: https://sites.google.com/site/informatpadalko/ce-cikavo/cikava-matematika/pro-istoriu-viniknenna-vid-emnih-cisel
3. Терещенко Владислава. Конспект Додавання раціональних чисел. Режим доступу https://web.archive.org/web/20220120052904/https://vseosvita.ua/library/urok-dodavanna-racionalnih-cisel-109288.html
4. Сафронова Світлана. Конспект Додавання раціональних чисел. Режим доступу https://naurok.com.ua/rozrobka-vidkritogo-uroku-v-6-klasi-164058.html