УРОК 3

Тема уроку: Побудова графіків функцій за допомогою геомет­ричних перетворень відомих графіків функцій.

Мета уроку: Формування умінь будувати графіки функцій за до­помогою восьми базових перетворень графіка функції у = f(x): у = -f(x);    у = f(-x); у = f(x) + b; у = f(x + a); у = af(x); у = f(ax); у = f(│x│);   у = │f(x)│.

І. Перевірка домашнього завдання.

1. Розв'язування вправ, аналогічних до домашніх.

1) Знайдіть область визначення функції:

а) ;  б) .

Розв'язання

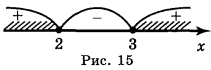
а) Через те що арифметичний квадратний корінь існує лише з не­від'ємних чисел, х² - 5х + 6 0 . Розв'яжемо нерівність методом інтервалів (знайдемо нулі функції g = х² - 5х + 6, нанесемо їх на координатну пряму і визначимо знак функції на кожному про­міжку) (рис. 15).

Отже, D(y) = (-; 2][3; +).

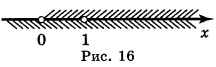
б) D(y) знаходимо розв'язавши систему 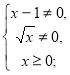.  Отже, D(y) = (0; 1)(1; +)  (рис. 16).        

2) Дослідіть на парність і непарність функцію:

а) f(x) = х²(2x - х³) ; б)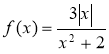

Розв'язання

а) Через те що D(f) = R і f(-x) = (-х)(2(-х) - (-х)³) = х²(-2х + х³) = -x²(2x - х³) = -f(x), f(x) = x²(2x –х³) — непарна.

б) Через те що D(f) = R і 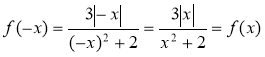 , то 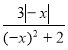– парна .

II. Повторення і систематизація знань учнів про геометричні перетворення графіків.

Запас функцій, графіки яких ви вмієте будувати, поки неве­ликий. Але використовуючи відомі із курсів геометрії і алгебри відомості про перетворення фігур, цей список можна суттєво розширити. Згадаємо елементарні перетворення графіка функції у = f(x) за допомогою таблиці 2.

III. Формування умінь будувати графіки за допомогою геометричних перетворень відомих графіків.

Колективне виконання вправ № 3 (1; 2; 3; 14; 19).

IV. Підсумок уроку.

V. Домашнє завдання.

Розділ І § 1 (3). Запитання і завдання для повторення № 27-31. Вправа № 3 (7, 8, 9, 4, 5, 6, 18).

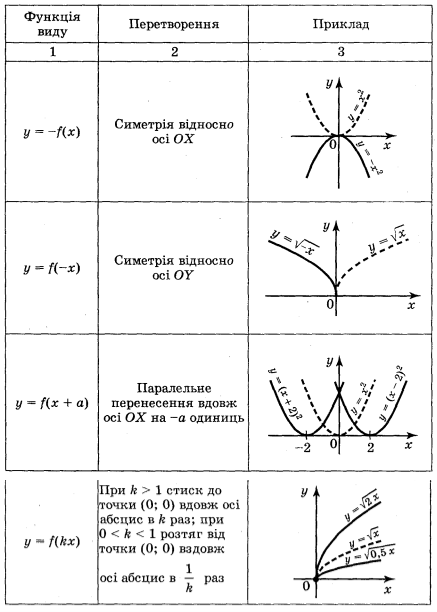
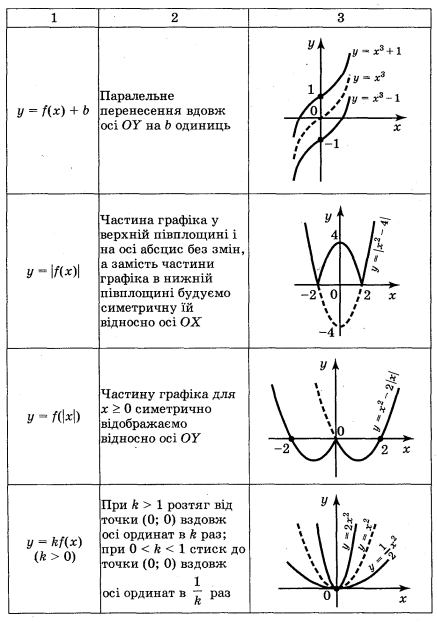Таблиця 2