УРОК 6

Тема уроку: Радіанна міра кутів і дуг.

Мета уроку: Узагальнення і систематизація знань учнів про радіанну міру вимірювання кутів і дуг. Формування умінь визначати радіанну міру кута за градусами і навпаки.

І. Перевірка домашнього завдання.

1. Перевірку виконання вправ № 4, 5 здійсніть по записах, зроб­лених до початку уроку.

2. Математичний диктант.

1) Кутом якої чверті є кут 370°?

2) Запишіть всі кути повороту, кінцевий радіус яких знахо­диться на додатній півосі ΟΥ?

3) Обчисліть: 2cos 60° + 2sin 30°.

4) Знайдіть cos 720°.

5) Знайдіть sin (-270°).

6) Який знак має tg (-50°).

Відповідь: 1) І; 2) 90° + 360°n, n Ζ; 3) 2; 4) 1; 5) 1; 6) -.

II. Сприймання і усвідомлення нового матеріалу.

Як відомо, кути вимірюються в градусах, хвилинах, секундах,

Градусом називається частина розгорнутого кута.

Таким чином, розгорнутий кут дорівнює 180°, прямий кут дорівнює 90°.

Між градусами, хвилинами і секундами існують співвідно­шення: 1º = 60', 1' = 60'', 1' = , 1' = . Крім градусної міри, використовуються і інші одиниці вимі­рювання кутів. У математиці і фізиці це радіанна міра кута.

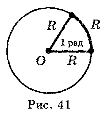
1 радіан — центральний кут, який опирається на дугу, довжина якої дорівнює радіусу (рис. 41).

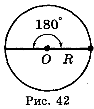
Установимо зв’язок між радіанним і градусним вимірюванням кутів. Куту, що дорівнює 180°, відповідає півколо, тобто дуга, довжина якої дорівнює πR (рис. 42). Щоб знайти радіанну міру кута в 180°, треба довжину дуги π-R розділити на

довжину радіуса R: 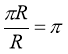. Отже, радіанна міра кута в 180° дорівнює π:

180° = π рад

Із цієї формули одержуємо (розділивши ліву і праву частини рівності на 180):

1° = рад, або 1° 0,017 рад.

Із рівності 180° = π рад також одержуємо (розділивши ліву і праву частини рівності на π):

1 рад = , або 1 рад 57°.

Розглянемо приклади переходу від радіанної міри до градус­ної і навпаки.

Приклад 1. Виразіть в радіанах величини кутів 30°; 45°; 60°; 90°.

Розділивши ліву і праву частини рівності: 180° = π рад послідов­но на 6, 4, 3, 2, одержуємо: 30° = рад, 45° = рад, 60° = рад; 90° = рад.

Приклад 2. Виразіть в градусах величини кутів рад, рад, рад, рад.

Розділивши ліву і праву частини рівності: 180° = π рад послідовно на 10; 5; 12; 18, одержуємо: рад = 18º; рад = 36º; рад = 15º; рад = 10º.

Приклад 3. Знайдіть в градусах 3,5 рад.

Через те що 1 рад = , 3,5 рад  = 3,5 ·   = = 201° .

Приклад 4. Знайдіть радіанну міру кута в 72°.

Через те що 1° = рад, 72° = 72 · рад = рад 1,3 рад.

При записі радіанної міри кута позначення «рад» опускають. Наприклад, замість рівності 90° = рад, пишуть 90° = .

Радіанна міра кута зручна для обчислення довжини дуги кола. Через те що кут в 1 радіан стягує дугу, довжина якої дорівнює R, то кут в α радіан стягує дугу довжиною: l = αR.

Якщо радіус кола дорівнює одиниці, то l = α, тобто довжина дуги дорівнює величині центрального кута, що опирається на цю дугу в радіанах.

III. формування умінь визначати радіанну міру кута за градусною і навпаки.

Виконання вправ

1. Запишіть у радіанній мірі кути: а) 120°;       б) 300°;       в) -405°;      г) -22,5°.

Відповідь: а) ;      б) ;     в) ;  г) .

2. Подайте в градусній мірі кути: а) ;        б) 2,5π;       в) 0,3π;       г) .

Відповідь: а) 135°;      б) 450°;     в) 54°;      г) 660°.

3. Подайте в радіанній мірі кути (скористуйтеся таблицями або калькулятором):

а) 20° 12';    б) 54° 23';    в) 136° 27';    г) 127° 15'.

Відповідь: а) 0,3586;   6)0,9492;  в) 2,3815;  г) 2,221.

4. Подайте в градусній мірі кути (скористайтеся таблицями або калькулятором):

а) 15;        б) 2;          в) 1,1417;     г) 4,3982.

Відповідь: а) 859,87°;   б) 114,65°;   в) 65° 25';   г) 252°.

IV. Підведення підсумків уроку.

V. Домашнє завдання.

Розділ І § 3. Запитання і завдання для повторення № 35—39. Вправи № 8, 9.