Конспект уроку на тему "Формула коренів квадратного рівняння. Розв'язування квадратних рівнянь" 8 клас

Широківська ЗОШ І-ІІІ ст.

 

 

 

 

 

Конспект уроку

алгебри у 8 класу

на тему

«Формула коренів квадратного рівняння.

Розв'язування квадратних рівнянь.»

 

 

 

 

 

 

 

 

 

 

Підготувала

вч. математики

Попович С.І.

 

 

 

 

 

 

      Тема уроку. Формула коренів квадратного рівняння.

Мета уроку: Вивести формулу коренів квадратного рівняння;

навчити учнів застосовувати її до розв'язання квадратних рівнянь;

розвивати логічне та алгоритмічне мислення, увагу, культуру мови і запису;

виховувати дружелюбність, свідоме ставлення до вивчення математики.

Учні повинні:

розпізнавати повне квадратне рівняння і визначати його  коефіцієнти;

визначати кількість коренів квадратного рівняння залежно від знаку дискримінанта;

знати формулу дискримінанта та коренів квадратного  рівняння, застосовувати ці формули при розв’язуванні вправ;

визначати кількість коренів рівняння залежно від знаку дискримінанта.

Тип уроку. Урок засвоєння нових знань.

Обладнання. Таблиця „Квадратні рівняння”, картки-завдання для індивідуальної роботи;  мультимедійний  проектор.

               Девіз: Знати , мислити ,     вміти, діяти.

ХІД УРОКУ

1. Організаційний момент.

ІІ. Перевірка виконання домашнього завдання.

1. Вправу №746  перевірити коментуванням з місця, до № 748* рівняння записати на дошці.

2. Ліквідація знайдених недоліків.

Завдання на карточках ( на дошці )

1-й учень: х²  - 25 = 0;  х² + 20 = 0;

2-й учень:  х² -1/9=0;  3 х²  – 27=0

3-й учень: 4 х²  + х  = 0; х² -4х+4=0

   З рештою учнів:

ІІІ. Актуалізація опорних знань учнів.

1) Вправа “Я - тобі, ти – мені” 

2) Назвати коефіцієнти квадратних рівнянь:                      (Слайд 4)

а) 2 х² +3х-2=0;  б) 4-у² -3у=0; в) х²  -4=5х; г) -5х+2- 4 х² =0.

3) Скласти квадратне рівняння, якщо відомі коефіцієнти:

а	b	с
2	0	-5
-1	2	0
5	3	-2
4	-3	2

 

4) Які з рівнянь не мають коренів:

   а) 3 х²  =-9; б) -5 х² = -2; в) х² +121=0? Чому?

      5) Віднови записи                                                                (Слайд5)

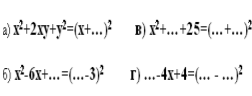
       6)Розв’язати рівняння:

  а) 16х² + 8х + 1 = 0; б) х² – 6х + 9 = 0.

IV.    Мотивація навчальної діяльності.

Учитель. Ми  навчилися розв’язувати неповні квадратні рівняння  й повні квадратні рівняння, в яких легко можна виділити квадрат двочлена. А як же розв’язувати квадратні рівняння, в яких виділення повного квадрата ускладнене?

Формулювання проблеми: не­обхідно знайти єдиний достатньо простий алгоритм розв'язання квад­ратних рівнянь загального вигляду. Розв'язання цієї проблеми і є голов­ною метою уроку.                  (Слайди1-3)

V. Вивчення нового матеріалу.

       1. Виведемо формулу коренів квадратного рівняння ах² + bх + с = 0.

Помножимо обидві частини рівняння на 4а (а ≠ 0), матимемо:

4а²х² + 4аbх 4ас = 0,

(2ах)² + 2∙2ах∙b + b² – b² + 4ас = 0,

(2ах + b)² – b² + 4ас = 0,

(2ах + b)² = b² – 4ас.

      Вираз  b² – 4ас називають дискримінантом (від латинського diskriminns – той, що розрізняє) даного рівняння і позначають буквою D. Тоді  (2ах + b)²  = D. За значенням D можна визначити кількість коренів квадратного рівняння ах² + bх + с = 0.

1. Встановимо залежність коренів рівняння від дискримінанта.

Запитання для учнів:

  – Скільки коренів може мати рівняння (2ах + b)² = D і від чого це буде залежати?

Розглядаємо випадки:

1) Якщо D > 0, то

              2ах + b =         або          2ах + b = –

              х =                                 х =.

Короткий запис:

x_1,2 = - формула  коренів квадратного рівняння.

2)  Якщо D = 0, то 2ах + b = 0,  х =  –   – єдиний корінь.

3)  Якщо D < 0, то дане рівняння не має коренів, тому, що не існує такого значення х, для якого значення виразу  (2ах + b)²  було б від’ємним.

Користуючись  формулою коренів квадратного рівняння можна розв’язати будь-яке квадратне рівняння.

 (Звернути увагу на стенд в класній кімнаті «Розв’язання повних квадратних рівнянь за формулою» та розгляд слайду 6 на екрані.)

                                                                                                                                                      

 Запитання до учнів:

 - Який алгоритм «Розв’язання повних квадратних рівнянь за формулою» ? Форма запису розв’язування повних квадратних рівнянь за формулою  

Приклад. Розв’язати рівняння  2х² – 3х -2 = 0.                 (Слайд7)                              

D = b² - 4ас;  D = (−3)² − 42(-2) = 9 +16 = 25>0,

  рівняння має два  корені;  

x_1,2 = ; x_1,2 = ; х₁ = 2; х₂= -.

6. Закріплення вивченого матеріалу.                       (Слайд8)

1)Вправи 754,756 (усно)

2) Знайдіть дискримінант квадратного рівняння та кількість коренів: Вправа 757 – на дошці.

3) Розв'язати рівняння, користуючись формулою коренів: Вправа 759 (1, 2)- колективно, з  записами  на  дошці, (3- 6) – самостійно з наступною перевіркою  і              коментуванням  (по1 учневі працює               на               закритій дошці).                                                                                                Вправа 761 (1, 5)- на дошці, 2-4, 6 - робота в парах:

2 і 6 – І пара, 3 і 4 - ІІ пара

7.                              Підсумок уроку.                                                           (Слайд 9-10)

          

Формулюються висновки, які були зроблені на уроці. Коментуються теоретичні положення про формулу коренів квадратного рівняння. Виставляються оцінки.

IX.  Домашнє завдання.                                                      (Слайд11)

Підручник О.С. Істер   «Алгебра» 8кл. – К.: Освіта, 2008.

• Опрацювати § 21,
• Виконати вправи

СР-№ 758, 760;  ДР,ВР- 762, 763,772а*

• Вивчити формулу коренів квадратного рівняння