Науково-дослідницька робота "Трикутник Рьоло. Його властивості та застосування"

Міністерство освіти і науки України

Департамент освіти і науки Донецької облдержадміністрації

Донецьке територіальне відділення МАН України

 

 

 

 

                                                             Відділення : математика

                                                             Секція: математика

 

 

ФІГУРИ ПОСТІЙНОЇ ШИРИНИ.

ТРИКУТНИК РЬОЛО,

ЙОГО ВЛАСТИВОСТІ ТА ЗАСТОСУВАННЯ.

 

 

                      Роботу виконала:
Набока Аліна Костянтинівна
                                                 учениця 10-А класу Костянтинівської  спеціалізованої загальноосвітньої   школи

I-III ступенів № 6 з поглибленим

 вивченням окремих предметів

 

 

                            Науковий керівник:
                                         Кандибка Оксана Іванівна
                                        учитель математики  СЗШ № 6

 

 

 

Слов’янськ  –2017

ТЕЗИ.

 

Моя робота присвячена розгляду основних властивостей фігур постійної ширини.  Взагалі, далеко не всі знають, що таке діаметр, ширина фігури. Може скластися враження, що коло єдина опукла фігура, що має одну і ту ж ширину у різних  напрямках: ця ширина дорівнює діаметру кола. Але це невірно: є безліч випуклих фігур, які мають за всіма напрямками  однакову ширину. Найпростішим прикладом є трикутник Рьоло. У своїй роботі я доведу, що із усіх фігур постійної ширини трикутник Рьоло має найменшу площу, а це має неабияке прикладне значення, яке теж описане у моєму дослідженні.

Основна мета написання роботи:

Розширити коло досліджуваних у школі фігур та довести, що геометрія потрібна в практичному житті, знання цієї науки розкриває можливості діяльності людини.

Завдання наукового дослідження:

ознайомитись з фігурами постійної ширини, їх властивостями;

з’ясувати, як отримують фігури постійної ширини, навчитись будувати дані фігури;

розглянути застосування фігур постійної ширини для рішення задач;

показати роль і значення цих фігур.

Актуальність обраної теми.

Історично геометрія розпочиналася з трикутника, тому трикутник не лише символ геометрії, але і атом геометрії. Постійно відкриваються усе нові й нові властивості трикутника. Щоб розповісти про усі відомі його властивості, знадобиться том величиною в декілька тисяч сторінок. Геометрія трикутника дає можливість відчути красу математики взагалі і може стати для когось початком шляху в "велику науку". Кожен любитель геометрії трикутника має можливість відкрити щось нове і поповнити її скарбницю власною дорогоцінною знахідкою, бо геометрія воістину невичерпна. У сучасному світі при технологіях, що швидко розвиваються, не можна обійти фігуру постійної ширини - трикутника Рело, що дозволяє скоротити витрати при виробництві, приміром, при конструюванні деталей.

Робота може бути цікава як учителям так і учням, її можна використовувати в якості практичного посібника на факультативних заняттях з математики або на курсах за вибором у середній школі.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ЗМІСТ

Вступ…………………………………………………………………….…………5

РОЗДІЛ 1

Фігури постійної ширини , їх властивості

    1.1. Означення фігур постійної ширини……………………………………....8

    1.2. Властивості фігур постійної ширини…………………………………….9

РОЗДІЛ 2

Трикутник Рьоло

      2.1.Означення трикутника Рьоло…………………………………………...10

      2.2. Побудова трикутника Рьоло……………………………………………10

      2.3. Історичні  відомості……………………………………………………..11

      2.4. Властивості трикутника Рьоло……………………………………..…..12

РОЗДІЛ 3

Застосування трикутника Рьоло та інших фігур постійної ширини

  3.1. Двигун Ванкеля ………………………………......................................15

  3.2  Механізм Грейфера …………………………………………………....15

  3.3. Свердло для квадратних отворів………………………………….…...16

  3.4. Кулачковий механізм…………………………………………………..16

  3.5. Коток…………………………………………………………………….17

  3.6. Архітектура……………………………………………………….…….18

  3.7. Тренажери для розвитку різних груп м'язів……………………..……18

  3.8. Люки каналізації………………………………………………….…….19

  3.9. Музичні інструменти……………………………………………..……20

  3.10. Мотоіндустрія…………………………………………………..…......20

  3.11.  Монети та наукова фантастика………………………………..…….21

 РОЗДІЛ 4

Добірка задач з обчисленнями за темою «Многокутники Рьоло»…………...23

Висновок………………………………………………………………………….30 Список використаних джерел……………………………………………..……31

ВСТУП

На одному з сайтів я випадково побачила відео з науковцем, він дуже простою і зрозумілою мовою говорив про складні математичні речі. «Чому каналізаційні люки круглі?» - це питання , на  яке професор відповідав глядачам, запам’яталося мені. Питання «Чому люки круглі» задається фахівцями з підбору персоналу кандидатам. Говорять, що відповідь на дане питання дозволяє оцінити загальний рівень інтелекту, оцінити той факт, як людина поводиться в разі форс-мажорних обставин, яка у нього швидкість мислення, чи уміє він використовувати нестандартні підходи та інше.

Найважливіше  і те, як кандидат відповість на питання, серйозно або жартами. До речі, всесвітньо відома компанія Microsoft давно користується таким питанням при тестуванні фахівців, яких збираються брати на роботу.

Відео про люки - це початок мого зацікавлення фігурами постійної ширини.

Що ми знаємо про трикутник Рьоло з шкільного курсу – нічого.

Я познаймилася з «круглим» трикутником –трикутником Рьоло через Інтернет. Вирішила довідатися про цю геометричну фігуру і знайшла немало інформації.

Я  почала  з  ознайомлення властивостей фігури.  І  зупинилася  на  тих,  які  допоможуть  зрозуміти,  де ця фігура може бути  застосована. 

 Якщо в давні часи найширше застосовувався на практиці прямокутний трикутник Піфагора, то у наш час найбільший інтерес викликають незвичайні властивості трикутника Рело (Reuleaux Franz, 1829–1905).

Актуальність обраної теми:  кожен любитель геометрії трикутника має можливість відкрити щось нове і поповнити її скарбницю власною дорогоцінною знахідкою, бо геометрія воістину невичерпна. У сучасному світі при технологіях, що швидко розвиваються, не можна обійти фігуру постійної ширини - трикутника Рьоло, що дозволяє скоротити витрати при виробництві, приміром, при конструюванні деталей.

Мета написання роботи:  розширити коло досліджуваних у школі фігур та довести, що геометрія потрібна в практичному житті, знання цієї науки розкриває можливості діяльності людини.

Об'єкт дослідження : многокутники Рьоло

Предмет дослідження : практичне застосування властивостей трикутника Рьоло.

Задачі дослідження:

1. Дізнатися, що таке трикутник Рьоло?

2. Виділити його основні властивості.

3. Визначити, де зустрічається трикутник Рьоло, застосування його властивостей.

Інформаційною основою роботи є фігури постійної ширини.

Методи дослідження:

- теоретичний (вивчення і теоретичний аналіз наукової і спеціальної літератури; узагальнення досвіду);

- практичний (добірка завдань з обчисленнями за темою «Многокутники Рьоло»)

Моя робота присвячена розгляду основних властивостей фігур постійної ширини. Взагалі, мало хто знає, що таке діаметр, ширина фігури. Може здатися, що круг є єдиною опуклою фігурою, в якої ширина в будь-якому напрямі одна і та ж: вона дорівнює діаметру круга. Проте це не так: існує безліч фігур постійної ширини, тобто таких опуклих фігур, в яких на всіх напрямках ширина однакова. Простим прикладом є трикутник Рело. У своїй роботі я доводжу, що зі всіх фігур постійної ширини трикутник Рело має найменшу площу.

 

Робота може бути цікава як учителям так і учням, її можна використовувати у якості практичного посібника на факультативних заняттях з математики або на курсах за вибором в середній школі.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ОСНОВНА ЧАСТИНА

РОЗДІЛ 1

Фігури постійної ширини , їх властивості

 

 

 

1.1. Означення фігур постійної ширини

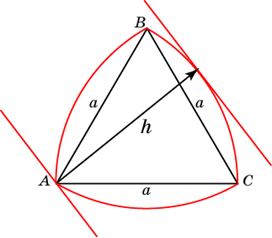
Крива постійної ширини a - плоска опукла крива, длинa ортогональної проекції якої на будь-яку пряму рівна a. Іншими словами, кривої постійної ширини називається плоска опукла крива, відстань між будь-якими двома паралельними опорними прямими якої постійно і рівне a - " ширині" кривої.

Для визначення ширини замкнутою кривою a розглянемо дві паралельні прямі, між якими розташована ця крива. Зрушуватимемо один до одного ці прямі до тих пір, поки вони не торкнуться кривої. Відстань між отриманими паралельними прямими і буде шириною кривою в напрямі перпендикулярному цим прямим.

 

 

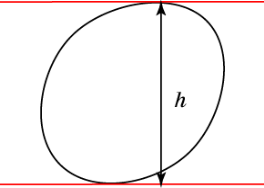
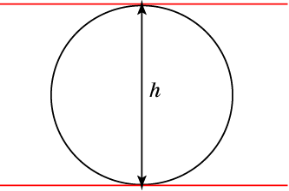
Рис.1.1.

Для різних напрямів ширина кривої може бути різною. Прикладом кривої однакової (постійною) ширини по усіх напрямах є коло. Її ширина дорівнює діаметру.

 

 

 

1.2. Властивості фігур постійної ширини

 

Ці властивості, загальні для всіх фігур сталої ширини.

• За теоремою Барб'є  довжина будь якої кривої постійної ширини дорівнює 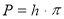 , де h – ширина кривої{\displaystyle \pi a}. Всі фігури постійної ширина h мають однаковий периметр.
• З кожною із своїх опорних прямих фігури постійної ширини мають лише по одній спільній точці.
• Відстань між двома довільними точками фігур постійної ширини {\displaystyle a} h не може перевищувати h {\displaystyle a}.
• Відрізок, що сполучає точки дотику двох паралельних опорних прямих до кривих постійної ширини, є перпендикуляром до цих опорних прямих;
• Через довільну точку границі фігури постійної ширини проходить хоча б одна опорна пряма.
• Радіус кола, що має не менше трьох спільних точок с границею фігури постійної ширини{\displaystyle a}, не перевищує h {\displaystyle a}.
• Будь-яку фігуру сталої ширини, можна вписати в квадрат, а також в правильний шестикутник.

 

 

 

 

 

 

 

 

 

 

РОЗДІЛ 2

Трикутник Рьоло

 

 

 

  2.1.Означення трикутника Рьоло

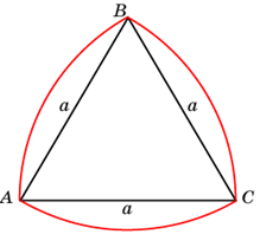
Трикутник Рьоло або "круглий трикутник" - плоска опукла геометрична фігура, проста після круга фігура постійної ширини.

 Трикутник Рьоло - це область перетину трьох кіл, побудованих з вершин правильного трикутника. Нерівна замкнута крива, що обмежує цю фігуру, також називається трикутником Рьоло. Якщо до трикутника Рьоло провести пару паралельних опорних прямих, то незалежно від вибраного напрямку відстань між ними буде постійною. Ця відстань називається шириною. Оскільки одна з прямих завжди проходить через вершину трикутника, а інша торкається протилежної дуги, то ширина трикутника дорівнює радіусу кругів, що утворюють його. Трикутник Рьоло відноситься до розряду простих фігур (як круг), що мають постійну ширину.

 

2.2. Побудова трикутника Рьоло

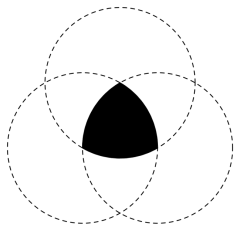  Таку  фігуру  дуже  просто  побудувати,  використовуючи  лише  циркуль.  Для цього  потрібно  провести  два  кола  з  однаковим  радіусом,  але  так, щоб  центр  другої  збігався  з  однією  з  точок  першої  (окрім  центру).  Проводимо  третє  коло,  так щоб  його центр  збігався  з  точкою  перетину  перших  кіл.  Область,  яка  належить  всім  трьом  колам  і  є  трикутник  Рьоло.

 

 

 

                                                         Рис.2.2.                                 

 

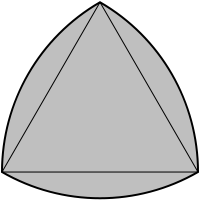
Інший спосіб – використовуючи правильний трикутник.

Будуємо три дуги з центрами в вершинах трикутника і радіусом, який дорівнює стороні цього ж трикутника.

 

 

 

 

 

2.3. Історичні  відомості

На думку істориків, назву цій " непростій" простій фігурі дав німецький механік Франц Рьоло, що жив з 1829 по 1905 роки. Багато істориків сходяться в тому, що саме він став першовідкривачем властивостей цієї геометричної фігури. Він перший широко використав властивості і можливості трикутника Рьоло у своїх механізмах.

Епоха, в якій жив і творив Рело Франц  можна назвати епохою філософствуючих інженерів, - Э.Гартиг, Фр.Рело і А.Ридлер і перших філософів техніки - Э.Капп, А.Эспинас, Ф.Бон. Що ж до робіт Ф.Рело, то треба відмітити, що в 1854 р. він в співавторстві з Моллем видав перший том "Конструювання в машинобудуванні". У 1875 р. Рело опублікував перший том "Теоретичної кінематики". Рело був не лише ученим, але і практиком : він був членом жюрі на міжнародних виставках в Парижі , Відні , Філадельфії . Аналізуючи стан германської промисловості, він вимагав підвищення якості її виробів. А також Рело любив мистецтво. Він переклав

німецькою мовою "Гімн про Гайавате" Лонгфелло, багато малював і гравіював по дереву, писав про "художній стиль в машинобудуванні". Його "Подорож по Індії" - блискучий зразок художньої прози.

Рьоло не є першовідкривачем цієї фігури, хоча він і детально досліджував її. Зокрема, він розглядав питання про те, скільки контактів (у кінематичних парах) потрібні, щоб запобігти руху плоскої фігури, і на прикладі викривленого трикутника, вписаного в квадрат, показав, що навіть трьох контактів може бути недостатньо для того, щоб фігура не оберталася. Деякі математики вважають, що першим продемонстрував ідею трикутника з рівних дуг кола Леонард Ейлер в XVIII столітті. Проте, подібна фігура зустрічається і раніше, в XV столітті: її використав у своїх рукописах Леонардо да Вінчі. Трикутник Рьоло є в його манускриптах, що зберігаються в Інституті Франції, а також в Мадридському кодексі.

Приблизно у 1514 році Леонардо да Вінчі створив одну з перших у своєму роді карт світу. Поверхня земної кулі на ній була розділена екватором і двома меридіанами на вісім сферичних трикутників, які були показані на площині карти трикутниками Рьоло, зібраними по чотири навколо полюсів.

 

 

 

 

 

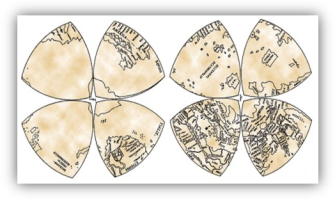
                                                                                                      Рис.2.3.

  2.4. Властивості трикутника Рьоло

Трикутник Рело, будучи фігурою сталої ширини, має всі властивості, що характерні для будь-якої іншої фігури з цього класу.

 

1) Побудова циркулем.

 Трикутник Рьоло можна побудувати за допомогою одного тільки циркуля, не прибігаючи до лінійки. Ця побудова зводиться до послідовного проведення трьох рівних кіл. Центр першої вибирається довільно, центром другої може бути будь-яка точка першого кола, а центром третьої - будь-яка з двох точок перетину перших двох кіл.

2) Найменша площа

 Серед усіх фігур постійної ширини a у трикутника Рьоло найменша площа. Визначити площу трикутника Рьоло можна додаванням до площі рівносторонього трикутника{\displaystyle S_{\triangle }={{\sqrt {3}} \over {4}}\cdot a^{2}}площ трьох однакових кругових сегментів, що спираються на кут у 60°. {\displaystyle S_{seg}={{a^{2}} \over {2}}\left({{\pi } \over {3}}-\sin {{\pi } \over {3}}\right)={\left({{\pi } \over {6}}-{{\sqrt {3}} \over {4}}\right)\cdot a^{2}},}Тоді площа трикутника Рело становить:

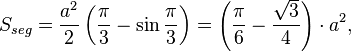
Фігура, що має протилежну граничну властивість — круг. Серед усіх фігур заданої сталої ширини його площа {\displaystyle S_{\circ }=a^{2}\cdot {{\pi } \over {4}}=a^{2}\cdot 0{,}78539\ldots }є максимальною. Однак площа відповідного трикутника Рело менша лише на ~10,27%. В цих незначних межах лежать площі усіх фігур заданої сталої ширини.

Чудові точки трикутника: центри вписаної, описаною кіл, ортоцентр і центр тяжіння співпадають. Радіуси вписаної і описаної кіл трикутника Рело  дорівнює:

 

             

 

 

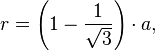
3) Найменший кут .

Через кожну вершину трикутника Рьоло, на відміну від інших його граничних точок, проходить не одна опорна пряма, а нескінченна безліч опорних прямих. Перетинаючись у вершині, вони утворюють " пучок". Кут між крайніми прямими цього " пучка" називається кутом при вершині. Для фігур постійної ширини кут при вершинах не може бути менше 120°. Єдина фігура постійної ширини, що має кути, рівні в точності 120°, - це трикутник Рьоло.

 

5) Найменша центральна симетрія .

З усіх фігур постійної ширини трикутник Рьоло має центральну симетрію в найменшій мірі.

 

6) Центр трикутника Рьоло – це точка перетину всіх медіан,

бісектрис і висот його правильного трикутника .

 

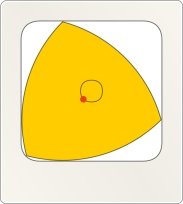7) Кочення по квадрату.

Будь-яка фігура постійної ширини вписана в квадрат із стороною, рівній ширині фігури, причому напрям сторін квадрата може бути вибраний довільно. Трикутник Рело - не виключення, він вписаний в квадрат і може обертатися в нім, постійно торкаючись усіх чотирьох сторін.

Кожна вершина трикутника при його обертанні " проходить" майже увесь периметр квадрата, відхиляючись від цієї траєкторії лише в кутах - там вершина описує дугу еліпса. Різниця з площею квадрата складає всього близько 1,2 %, тому на основі трикутника Рело створюють свердла, які дозволяють отримувати практично квадратні отвори.

 

РОЗДІЛ 3

Застосування трикутника Рьоло та інших фігур постійної ширини

 

 

 

Вивчивши наукову і довідкову літературу по трикутнику Рьоло, я виділила  декілька сфер застосування фігури постійної ширини.

3.1.   Двигун Ванкеля

У двигуні Ванкеля важлива  форма ротора. Ротор обертається усередині камери, поверхня якої виконана по епітрохоїді.

                                                                                                                 Рис.3.1.

Вал ротора жорстко сполучений із зубчастим колесом, яке зчеплене з нерухомою шестерінкою. Такий тригранний ротор обкатується навколо шестерні, торкаючись вершинами внутрішніх стінок двигуна і утворюючи три області змінного об'єму, кожна з яких по черзі є камерою згорання. Завдяки цьому двигун виконує три повних робочих циклів за один оборот.

Уперше на серійних автомобілях цей двигун стала встановлювати компанія Mazda. Він встановлений на моделях Mazda RX - 7 і Mazda RX - 8.

 

3.2. У кінематографії, а точніше - " механізм Грейфера", який здійснює покадрове переміщення плівки в кінопроекторах.

 

 

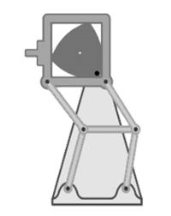В даному випадку трикутник Рьоло знаходиться усередині квадрата і рухає рамку, за допомогою обертання навколо одного зі своїх кутів. Зуб, який знаходитися на рамці, входить в перфорацію кіноплівки, протягає її на один кадр вниз і виходить назад.

 

 

 

3.3.  За допомогою свердла форми трикутника Рьоло можна свердлити квадратні отвори. Вершини трикутника Рьоло описують квадрат тільки при обертанні центру по фігурі такої, що складається з 4 дуг еліпсів.

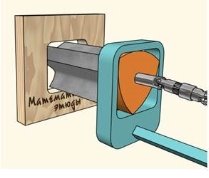  Рис.3.3.

 Звідси і складність створення такого свердла, оскільки звичайний дриль обертає свердло навколо своєї осі. Таке свердло сконструював Гаррі Уаттсу в 1917 році.

3.4. Кулачковий механізм.

Трикутник Рьоло використовувався в кулачкових механізмах деяких парових двигунів початку XIX століття. У цих механізмах обертальний рух кривошипа повертає трикутник Рело, який прикріплений до штовхача двома передавальними важелями і змушує його здійснювати зворотно-поступальний рух. За термінологією Рьоло, це з'єднання утворює «вищу» кінематичну пару, оскільки контакт ланок відбувається по лінії, а не по поверхні. У такого роду кулачкових механізмах штовхач при досягненні крайнього правого чи лівого положення залишається деякий скінченний проміжок часу нерухомим.

Трикутник Рело раніше широко застосовується в кулачкових механізмах швейних машин зигзагоподібної строчки.

Як кулачок трикутник Рело використовують німецькі годинникарі мануфактури A. Lange & Söhne в механізмі наручних годинників «Lange 31».

3.5. Коток.

(Котки з перерізом у вигляді круга і трикутника Рело. 

Німецький технічний музей)

Для переміщення важких предметів на невеликі відстані можна використовувати не тільки колісні, але і простіші конструкції, наприклад, циліндричні котки. Для цього вантаж слід розмістити на плоскій підставці, що встановлена на котках, а далі штовхати його. По мірі вивільнення задніх котків їх переносити і класти спереду. Такий спосіб транспортування людство використовувало до винаходу колеса.

При цьому переміщенні важливо, щоб вантаж не рухався вгору і вниз, оскільки тряска вимагатиме додаткових зусиль від того, хто штовхає  Для того, щоб рух по котках був прямолінійним, їхній переріз повинен бути фігурою сталої ширини. Найчастіше в перерізі був круг, адже котками служили звичайні колоди. Однак переріз у вигляді трикутника Рело дасть не гіршу можливість пересувати предмети так же прямолінійно.

3.6. Архітектура.

Вежа Кельнський трикутник

Форма трикутника Рьоло використовується також і в архітектурних цілях. Конструкція з двох його дуг утворює характерну для готичного стилю стрілчасту арку, однак цілком він зустрічається в готичних спорудах досить рідко. Вікна у формі трикутника Рьоло можна бачити в церкві Богоматері в Брюгге, а також у шотландській церкві в Аделаїді. Як елемент орнаменту він зустрічається на віконних гратах цистерціанського абатствав швейцарській комуні Гаутеріф (Фрибург).

Трикутник Рело використовують і в архітектурі, яка не належить до готичного стилю. Наприклад, побудована в 2006 році в Кельні 103-метрова вежа під назвою «Кельнський трикутник» в перетині має саме форму цієї фігури.

 

3.7.  Тренажери для тринування різних груп м'язів. Головна мета сучасних тренажерів, це ізольоване тренування м'яза. Але час не стоїть на місці і біомеханіка, дозволила зрозуміти, що важливо не лише ізолювати м'яз, але і правильно надавати на нього навантаження. Оскільки м'яз не здатний однаково сильно працювати упродовж усього свого "робочого ходу", то потрібно давати слабке навантаження в мить, коли він знаходиться в одному з крайніх положень і коли проходить " центральне" положення, навантаження може зростати. Але такий ефект складно отримати, для цього використовують різні кулачковоблочні механізми, і такі тренажери відрізняються великою ціною. У свою чергу використання трикутника Рьоло для цієї мети дуже ефективно замінює усі складні механізми. Якщо тягнути трос не через кулачковоблочний механізм, а через блок у вигляді трикутника Рьоло, то економитися приблизно 2 метри тросу, який проходить через таку систему, і скорочується витрата метала. Навантаження буде з початку зростати, а потім воно стане піковим у момент проходження вершини трикутника Рьоло, а потім знову сходити нанівець, за умови, що ми тягнемо одну і ту ж вагу. Навантаження на м'яз йде плавне і рівномірне.

 

3.8. Люки каналізації.

 Фігура постійної ширини не може проходити через отвір такої ж фігури з меншою шириною. Завдяки чому можна трикутник Рьоло використати і в цьому напрямку теж. Тут, звичайно, можна міркувати, що і круглий люк не провалюється, оскільки круг теж фігура постійної величини, але нам вже відомий той факт, що у трикутника Рьоло менше площа, ніж у круга, а значить і матеріалу менше витрачається на кришку люка. Це придумала не я. Але я думаю це актуально і зараз. У формі трикутника Рьоло можна виготовляти кришки для люків - досвідченим шляхом доведено, що завдяки постійній ширині вони не можуть провалитися в люк. У Сан-Франциско, для системи рекуперації води корпусу люків мають форму трикутника Рьоло. За рахунок того, що у трикутника Рьоло площа менша, ніж у круга, собівартість люків у формі трикутників Рьоло була б нижча, ніж у традиційно круглих. Перейшовши на серійне виробництво люків у формі трикутника Рьоло, на мій погляд, можна було б швидше розв'язати проблему відкритих колодязів і уникнути травматизму і смертей людей.

    Рис.3.8.

3.9. Музичні інструменти.

 Я неодноразово бачила баяни. Тому знаю, які мінуси є у цього інструменту. Один з них це те, що при натисненні на клавіші що близько стоять в 2 і 3 ряду вони чіпляють один за одного з причини невеликого змішення, що не прийнятно. Якщо ж клавіші зробити у формі трикутника Рьоло, і розташувати їх, як показано на рис.3.9, то такої проблеми можна уникнути. Причому інструмент буде екстравагантнішим. 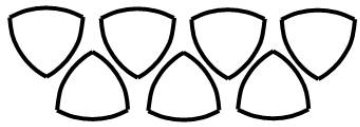рис.3.9.

 

Всі бачили медіатор музикантів-струнників, вони теж випускаються у формі трикутника Рьоло.

 

3.10.  Також можна знайти застосування трикутника Рьоло в мотоіндустрії. Від хлопців, які захоплюються мотоциклами, я багато чула про ручку газу. Усім відомо, для того, щоб приводити мотоцикл в рух необхідно "крутити цю ручку газу". У мотоіндустрії проблема з хорошим хватом цієї ручки стоїть гостро. Її вирішували по-різному, приміром: використовуючи матеріали, що підвищують тертя між рукавичкою і грипсою (ручкою газу). До того ж, при тривалій їзді рука просто втомлюється. Заради вирішення цієї проблеми, я думаю, було б доречно використовувати ручку, яка при фронтальному розрізі мала б форму трикутника Рьоло і, як виявляється, ідеально повторювала б внутрішні контури закритої долоні, і утримувати таку рукоять набагато легше.

Як виявилося, при простому вивченні вашої долоні ви побачите, що якщо зібрати руку " трубочкою", неначе ви тримаєте що-небудь кругле, то друга і третя фаланга другого, третього і четвертого, а також друга фаланга першого пальця (що замикає " кільце" з вашої долоні) утворюють вершини круглого трикутника, що повністю доводить мою гіпотезу. Це відкриття можна використати не лише для ручок мотоцикла, але і скрізь де необхідно утримувати з опором поворотну рукоять такого типу.

3.11. Форма многокутників Рьоло використовується в монетній справі. Наприклад, монети 20 і 50 пенсів Великобританії виконані у вигляді правильного семикутника Рьоло.

 

 

Існує виготовлений китайським офіцером велосипед, колеса якого мають форму правильного трикутника і п'ятикутника Рьоло.

  Рис.3.11.

 

У науково-фантастичній розповіді Пола Андерсона "Трикутне колесо" екіпаж землян вчинив аварійну посадку на планеті, населення якої не використовувало колеса, оскільки усе кругле знаходилося під релігійною забороною. У сотнях кілометрів від місця посадки попередня земна експедиція залишила склад із запасними частинами, але перенести звідти необхідний для корабля двотонний атомний генератор без яких-небудь механізмів було неможливо. У результаті землянам вдалося дотриматися табу і перевезти генератор, використовуючи катки з перерізом у вигляді трикутника Рьоло.

 

 

 

 

 

 

 

 

 

 

 

 

 

РОЗДІЛ 4

Добірка задач з обчисленнями за темою «Многокутники Рьоло»

 

 

 

Задача № 1.

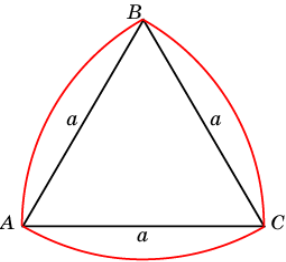
Доведіть, що периметр трикутника Рьоло дорівнює довжині кола, діаметр якого дорівнює ширині трикутника Рьоло.

 

Доведення

 

Нагадаємо, що довжина дуги кола з центральним кутом φ і радіусом r рівна φr. Оскільки трикутник Рело складається з трьох дуг кіл, для яких r = a, φ = π/3, то їх загальна довжина дорівнює  Р=3 (π/3)r=πr, тобто дорівнює довжині кола, діаметр якого дорівнює ширині трикутника Рело.

щтбд

 

 

 

 

 

 

Задача № 2.

Знайдіть кути трикутника Рьоло, утворені дотичними до дуг кіл в його вершинах.

 

 

Розв’язання.

 

Розглянемо коло(А;АВ), ВР – дотична до даного кола, точка В – точка дотику.

АВР = 90⁰ – за властивістю дотичної.

АВС = 60⁰ - АВС – рівносторонній. Отже, СВР = 90⁰ - 60⁰ =30⁰. Аналогічно, МВА = 30⁰. МВР  = 30⁰ + 30⁰ +60⁰ =120⁰.

 

Відповідь: 120⁰.

 

 

 

 

 

 

 

Задача № 3.

 

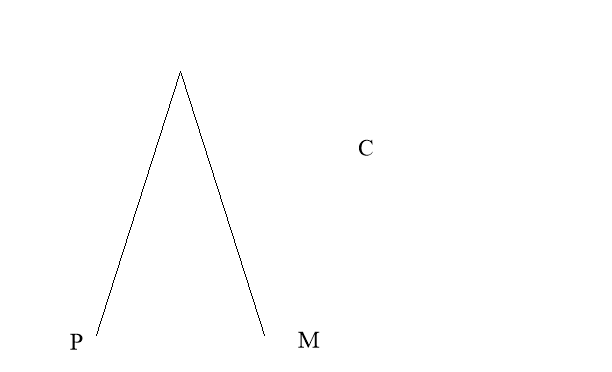
 Сторона правильного п'ятикутника дорівнює 1. Знайдіть ширину відповідного п'ятикутника Рьоло.

 

 

 

 

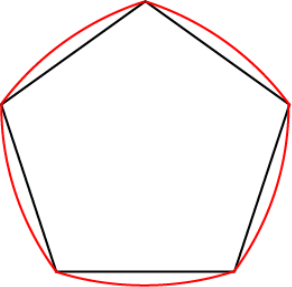
Розв’язання.

Розглянемо коло (В;ВР), тоді РМ – це сторона правильного десятикутника , вписаного в це коло, ВР  - радіус описаного кола і ширина п’ятикутника Рьоло.

R =;   РМ = 1 ( за умовою).

Отже, R =;

 

Об’єднуючи початок і кінець виразу, отримаємо квадратне рівняння. Розв’яжемо його способом заміни змінної і отримаємо результат:

;

.

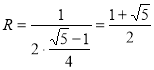Відповідь :

 

 

Задача № 4.

 

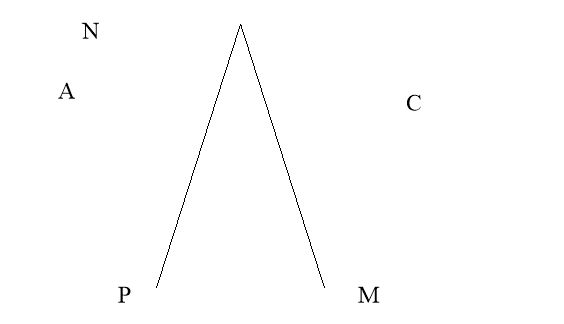
Знайдіть кути п'ятикутника Рело, утворені дотичними до дуг кіл в його вершинах.

 

 

 

 

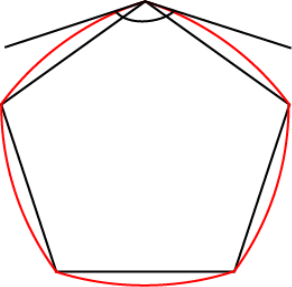
Розв’язання.

PBD=90⁰ – за властивістю дотичної;

РВМ= MBC = 36⁰  (АВС=108⁰  - кут правильного п’ятикутника );

MBD = 90⁰ – 36⁰ - 36⁰ = 18⁰;

NBD = 108⁰ + 18⁰ +18⁰ = 144⁰.

 

Відповідь: 144⁰.

 

Задача № 5.

 

Знайти радіуси вписанного та описанного кола для трикутника Рьоло, ширина якого a см.

 

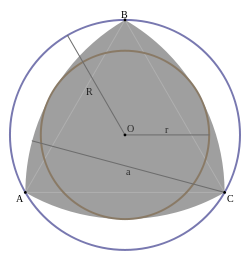
Розв’язання .

Радіус описаного кола знаходимо як радіус кола, описаного біля правильного трикутника АВС. .

;  .

Відповідь: ;  .

 

 

 

Задача № 6.

Знайдіть площу трикутника Рьоло з заданою шириною a .

 

Розв’язання.

Визначити площу трикутника Рьоло можна відніманням від потрійної площі сектора трикутника з центром в будь-якій вершині трикутника Рьоло  з центральним кутом 60° подвоєної площі рівностороннього трикутника АВС {\displaystyle S_{\triangle }={{\sqrt {3}} \over {4}}\cdot a^{2}}. {\displaystyle S_{seg}={{a^{2}} \over {2}}\left({{\pi } \over {3}}-\sin {{\pi } \over {3}}\right)={\left({{\pi } \over {6}}-{{\sqrt {3}} \over {4}}\right)\cdot a^{2}},}Тоді площа трикутника Рело становить:

S = .

Відповідь: S .

 

 

 

 

 

 

 

 

 

 

 

 

 

Задача № 7.

Доведіть, що площа будь-якого n-кутника Рьоло більша за площу трикутника Рьоло.

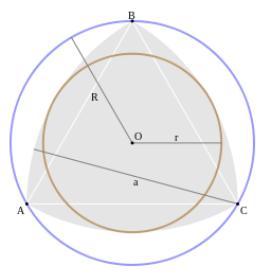
Доведення.

 

 

Площа n-кутника Рьоло до площі кола з діаметром d (d- ширина трикутника Рьоло), тобто , якщо . Площа трикутника Рьло знайдена в задачі № 6,   S = .

Знайдемо різницю між площею n-кутника Рьоло і трикутником Рьоло:

,отже

. Висновок: трикутник Рьоло має найменшу площу з усіх многокутників Рьоло.

щтбд

 

 

 

 

ВИСНОВКИ

 

 

Декілька тисяч років назад було винайдено колесо, яке зробило переворот в житті людини. Визначальною властивістю, наслідком якої стало технічне завоювання світу, стала властивість постійності ширини. Але, як виявилося, круг - не єдина фігура, яка має цю властивість. Мій інтерес, що викликав трикутник Рьоло, також належить цьому сімейству. У своїй роботі я не лише вивчила його властивості, геометричні характеристики, історію винаходу, але і розглянула сфери застосування цієї опуклої, симетричної фігури постійної ширини. Висунена мною гіпотеза про властивості цієї фігури знайшла своє підтвердження. Крім того, я відповіла для себе на низку запитань пізнавального характеру : які геометричні властивості забезпечують плавність ходу велосипеда з " трикутними" колесами, чому каналізаційні люки роблять круглими або у формі трикутника Рьоло? Не менш пізнавальною виявилася інформація про сфери застосування " круглого" трикутника не лише в техніці, але і в архітектурі, літературі. А також добрала і розв’язала низку задач до теми «Многокутники Рьло».

 Таким чином, поставлені мною завдання, реалізовані в повному об'ємі. Але є перспективи подальшої роботи в цьому напрямку: дослідити фігури постійної ширини, утворені відрізками прямих рівної довжини, які перетинаються. А також вивчити властивості об’ємних тіл постійної ширини.

Дослідницька робота була цікавою, незважаючи на труднощі, які виникли при доведенні властивостей фігур постійної ширини. Думаю, продовжити роботу далі і знайти більш детальну інформацію відносно даних фігур.

Дана робота розширює , дає можливість творчості при вирішенні завдань, вчить бачити і знаходити зв'язок між елементами трикутника.

Робота може бути цікава як учителям так і учням, її можна використовувати в якості практичного посібника на факультативних заняттях з математики або на курсах за вибором в середній школі.

СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ

 

1. А. Г. Конфорович. Визначні математичні задачі. – Київ, Радянська школа, 1981. – 189с.

2. І. А. Кушнір. Трикутник у задачах. – Київ, Либідь, 1994.- 104с.

3. Г. С. М. Коксетер, С. Л. Грейтцер. Нові зустрічі з геометрією. – М., 

      Наука, 1978. – 223с.

4. Дорофеєв, Г.В., Шаригін, И.Ф., Суворова, С.Б. Математика. – М.:Освіта,1987.

5. Коксетер, С.М., Грейтцер, С.Л. Нові зустрічі  з геометрією. – М., Наука, 1978.

6.  В. Г. Болтянский, І. М. Яглом. Опуклі фігури. М.—Л.: ГТТИ, 1951.

7. . Яглом И.М., Болтянский В.Г. Фігуры постійної ширини // Опуклі фігури. — М.-Л.: ГТТИ, 1951

8. «ІНТЕРНЕТ-РЕСУРСИ» - Режим доступу: http://xreferat.com/54/87-2-figury-postoyannoiy-shiriny-treugol-nik-relo.html