МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ

КРЕМЕНЧУЦЬКИЙ КОЛЕДЖ ТРАНСПОРТНОЇ ІНФРАСТРУКТУРИ

 

 

“ЗАСТОСУВАННЯ ПОХІДНОЇ 

ДО 

РОЗВ’ЯЗУВАННЯ 

ПРИКЛАДНИХ ЗАДАЧ”

 

заняття – конференція  (засідання «наукової ради») 

 

 

Підготували  Сухов О.В.  викладач ОВМ вищої категорії

 

 

 

 

 

 

 

 

                                                                                     Кременчук 2016                                                 

Сухов О.В.            Методична розробка “Застосування похідної до  розв’язування прикладних задач” заняття – конференція

(засідання «наукової ради»)  для студентів ІІ курсу денного відділення. 

                                                                 Для всіх спеціальностей. Кременчук, 2016р.

 

 

Методична розробка містить матеріал відповідно до типової навчальної програми з курсу ,,ОВМ” для ВНЗ І-ІІ рівнів акредитації. Методична розробка за “Застосування похідної до розв’язування прикладних задач” складається з двох частин: методичні вказівки «Проектна діяльність» та розробка уроку з ОВМ для студентів 2 курсу за темою “Застосування похідної до розв’язування прикладних задач”

Рекомендовано для студентів ВНЗ І-ІІ рівня акредитації.

 

 

 

Розглянуто

на засіданні циклової комісії природничо-математичних дисциплін ___   _______________  2016р. Голова циклової

комісії _____________ К.В. Гладун

 

 

 

Схвалено методичною радою КТЗТ Протокол № ______ від ____ ____________   2016 р.

Голова методичної ради

________________        К.М.Сотніков

             

Метод проектів

 

Основні задачі сучасної системи освіти:

Інтелектуальний та духовний розвиток особистості, формування критичного та творчого мислення, вміння працювати з інформацією.

 

Сучасні тенденції освіти:

Сучасна система освіти має на меті надання студентам можливості розмірковувати, співставляти різні точки зору, різні позиції, формулювати та аргументувати власну точку зору, спираючись на знання фактів, законів, закономірностей науки, на власні спостереження, свій та чужий досвід. 

 

Компетентність студентів у сфері вирішення проблем:

Під компетентністю в сфері вирішення проблем розуміють «здатність студента використовувати пізнавальні вміння для вирішення між предметних реальних проблем, в яких спосіб вирішення з першого погляду очевидно не визначається. Уміння, необхідні для рішення проблеми, формуються в різних навчальних сферах, а не тільки в рамках однієї з них – математичної, природничої чи гуманітарної». (The Pisa 2003 Assessment Framework, OECD, 2003)

 

Загальнонавчальні уміння, необхідні для вирішення проблем:

•      Розуміти проблему (використовувати знання та вміння для  розуміння інформації, запропонованої у вигляді текста, діаграми, схеми, формули, таблиці,  інтегрувати інформацію з різних джерел);

•      Характеризувати проблему (визначати перемінні, присутні в проблемі та зв’язок між ними, будувати гіпотези, критично оцінювати інформацію);

•      Представляти проблему (розробляти форму представлення інформації, переходити від однієї форми представлення до іншої);

•      Вирішувати проблему (приймати рішення з урахуванням умов поставленої проблеми, проводити аналіз системи, її планування для досягнення цілі);

•      Розмірковувати над рішенням  (досліджувати отримане рішення та в разі необхідності шукати додаткову інформацію, давати оцінку рішенню)

•      Повідомляти рішення проблеми (обирати форму представлення отриманого результа та викладати його зрозуміло для інших людей)

Метод проектів:

Сукупність прийомів, дій студентів у їх певній послідовності для досягнення поставленої задачі – рішення даної ПРОБЛЕМИ, важливої для студентів та оформленої у вигляді певного кінцевого ПРОДУКТУ.

 

Що таке навчальний проект:

З точки зору викладача:

•      Це завдання, що формулюють у вигляді проблем;

•      Цілеспрямована діяльність студентів;

•      Результат діяльності як знайдений ним спосіб розв’язання проблем^;

•      Це динамічний засіб розвитку, навчання та виховання який дозволяє відпрацьовувати необхідні уміння; З точки зору студента:

•      Це можливість зробити щось цікаве самостійно;

•      Це діяльність, яка дозволяє виявити себе, спробувати свої сили, докласти свої знання, принести користь та показати досягнуті результати.

        

Для чого нам потрібен метод проектів:

•      Навчити студентів самостійному, критичному мисленню.

•      Розмірковувати, спираючись на знання фактів, закономірностей науки, робити обґрунтовані висновки.

•      Приймати самостійні аргументовані рішення.

•      Навчити працювати в команді, виконуючи різні соціальні ролі.

Сутність методу проектів:

•      _{Проблема;}

•      Пошук способів;

•      Дослідницька, пошукова та інші види діяльності;

•      Оформлення проекту;

•      Захист проекту;

•      Прогнозування нових проблем.

 

Взаємозв’язок метода проектів з іншими методами особистісно орієнтованого підходу:

•      Навчання у співробітництві;

•      Рольові ігри;

•      Дискусії;

•      Мозковий штурм;  Портфель студента.

Сукупність методів, які використовуються в проектній діяльності:,

•      Пошукові, , дослідницькі, наукові методи;

•      Дискусії, евристичний метод, мозкові атаки, рольові ігри.

Інтелектуальні вміння, необхідні при використанні метода проектів.

•      Вміння предметної області знань :

Ø сукупність відповідних компетенцій 

Ø ключові компетенції 

•      Інтелектуальні вміння критичного мислення :

Ø Пошук інформації 

Ø Осмислення

Ø Аналіз

Ø Синтез

Ø Застосування

Ø Оцінка

•      Комунікативні  вміння :

Ø Вміння спільної діяльності 

Ø Вміння дискутувати, приймати рішення 

 

Рівні проблемності:

Загальним приводом для рівневого розгляду проблемності є  ступінь самостійної  розумової діяльності студентів:

•      Перший рівень співвідноситься з проблемним викладенням навчального матеріалу викладача. 

•      Другий рівень  означає, що викладач створює проблемну ситуацію і разом з студентами вирішує її . 

•      Третій рівень  передбачає, що викладач створює проблемну ситуацію, а студент самостійно вирішує її. 

•      Четвертий рівень свідчить про повну самостійність студента, які  самі знаходять проблему і сам вирішує її, тим самим вирішуючи проблемну ситуацію, що виникла. 

Що таке критичне мислення?

•      По-перше, критичне мислення є вміння мислити  самостійно. 

•      По-друге, інформація є відправним, а  не кінцевим пунктом критичного мислення. Знання створює мотивацію, без якої людина не може мислити критично.

•      По-третє, критичне мислення починається з постановки питань і уяснення проблем, які потрібно вирішити.

•      По-четверте, критичне мислення прагне до  переконливої аргументації.

•      По-п’яте, критичне мислення є мисленням соціальним.

 

Етапи проведення проекту:

1.       Представлення проблемної ситуації:

-         вербально;

-         за допомогою відеоряду;

-         за допомогою мультимедійних засобів.

2.       Мозкова атака.

3.       Обговорення.

4.       Висування гіпотез.

5.       Визначення типу проекту.

6.       Організація малих груп співробітництва, розподіл ролей.

7.       Обговорення в групах стратегії дослідження, джерел інформації, способів оформлення результатів.

8.       Самостійна дослідна, пошукова робота учнів у відповідності  зі своїм завданням.

9.       Проміжні обговорення, дискусії, збір та обробка даних (на уроках, в науковому товаристві, в творчих майстернях, в медіатеці).

10.   Оформлення результатів проектної діяльності.

11.   Захист проекту, опанування, дискусія.

12.   Висунення, прогнозування нових проблем, що витікають із отриманих результатів.

13.   Самооцінка, зовнішня оцінка.

Критерії зовнішньої оцінки проекту:

•              значущість і актуальність висунутих проблем, відповідність тематиці, що вивчається; 

•              коректність використаних методів дослідження і методів обробки отриманих результатів;  активність кожного учасника проекту у відповідності до його індивідуальних здібностей; 

•              колективний характер прийнятих рішень; 

•              характер спілкування та взаємодопомоги   учасників проекту; 

•              необхідна і достатня глибина проникнення в проблему, залучення знань із інших областей; 

•              доказовість рішень, що приймаються, уміння аргументувати свої заключення та висновки; 

•              естетика оформлення результатів  проекту;   вміння відповідати на питання опонентів.

Координатор проекту:

•              мати гарні організаційні здібності;

•              бути методично грамотним ;

•              володіти навичками міжкультурного спілкування;

•              вміти встановлювати основані на довірі, відкриті, поважні відносини з студентами;

•              активно співпрацювати в проектній діяльності;

•              володіти базовими навичками праці в мережах;        вміти працювати з великими об’ємами інформації;            володіти новими телекомунікаційними технологіями.

Функції координатора проекту:

•              пошук учасників проекту;

•              при необхідності консультація (на прохання учасників проекту);

•              зв’язок з іншими організаціями, засобами масової інформації, спеціалістами, думка або знання яких потрібні учасникам проекту;

•              збір та розповсюдження інформації про учасників проекту;

•              стимулювання учасників до самооцінки;

•              організація захисту та зовнішньої оцінки проекту. 

           

ЕПІГРАФ ЗАНЯТТЯ: 

«Математика – наука молодих. Інакше і не може бути. Заняття математикою це – така гімнастика розуму, для якої потрібна вся гнучкість і вся витривалість молодості».

Н. ВІНЕР

 

Тема:

“Застосування похідної до розв’язання прикладних завдань.”

 

 

Мета:

Навчальна: Узагальнити і розширити знання студентів про вміння застосовувати методи диференціального числення до розв’язування прикладних задач, навчитися виділяти етапи в розв’язуванні прикладних задач;

Формування умінь та навичок: розвивати творче і логічне мислення, усне та писемне мовлення, розвивати вміння порівнювати і робити висновки, висловлювати свою думку; 

Виховна: виховувати в студентів бажання мати глибокі й міцні знання, працьовитість та уважність, розвивати вміння порівнювати і робити висновки, висловлювати свою думку; сприяти вихованню інтересу до математики.

 

 

Очікувальні результати:

Студенти повинні мати уявлення про похідну, знаходження похідних елементарних функцій, екстремальні точки, локальний екстремум функції, монотонність функції, знаходження найбільшого і найменшого значення функції, вміти застосовувати методи диференціального числення до розв’язування прикладних задач, виділяти етапи в розв’язуванні прикладних задач.

Тематичні питання:

1.   Що ми називаємо похідною?

2.   Як називається операція знаходження похідної;

3.   Яка функція називається спадною (зростаючою);

4.   Що таке монотонність функції;

5.   Що таке екстремум функції;

6.   Що називається критичною точкою;

7.   Схема знаходження найбільшого і найменшого значення функції.

 

Стислий опис застосування методу проектів на даному занятті:

У проекті досліджується вміння застосовувати методи диференціального числення до розв’язування прикладних задач; використання набутих знань при розв’язуванні задач як теоретичного так і практичного змісту.

 

Навчальні предмети, з якими пов’язаний проект:

Інформатика, історія, біологія, економіка, медицина, фізика, залізничний транспорт, філологія. 

Державні освітні стандарти та навчальні програми:

При опрацюванні даної теми узагальнюються й розширюються знання студентів про вміння застосовувати методи диференціального числення до розв’язування прикладних задач. Повторюються і систематизуються знання студентів про похідні, знаходження похідних елементарних функцій, точки екстремуму. В ході розв’язання задач розвиваються навички роботи з основними правилами знаходження похідних елементарних функцій. Удосконалюються й розвиваються вміння студентів використовувати апарат алгебри.

 

Навчальні цілі та очікувані результати навчання: 

Самостійно опрацьовувати додаткову літературу, робити висновки, працювати з Інтернетом, отримувати знання і використовувати їх на практиці з теми «Похідна і її застосування».

 

Діяльність студентів: 

1   день:

-   студенти ознайомлюються з завданням і вимогами, якими вони будуть керуватися під час роботи над проектом;

-   діляться на групи, отримують завдання;

-   здійснюють пошук інформації в Інтернеті та додатковій літературі; - добирають матеріал;

2   день:

-   набувають навичок працювати групами над узагальненням отриманої інформації;

-   розробляють план виступів;

3,4 день:

-   кожна група здійснює пошук задач та розв’язують їх; 5 день: 

-   проектують сценарій захисту своїх робіт, навчаються проводити публічні виступи; створюють загальну презентацію.

           

Студенти готуються до заняття заздалегідь: за декілька днів, підбирають задачі, шукають історичний матеріал. Перед заняттям група поділяється на 7 –м груп по три студенти в кожній, секретар Наукової ради. Коли починається заняття, студенти розсаджуються за столи на яких знаходяться таблички з назвами кафедр: історії, біології, економіки, медицини, математики та фізики, залізничного транспорту, філології.

Приблизний час, необхідний для реалізації навчального проекту:

-   5 днів та 1 заняття на демонстрацію та узагальнення теми.

Вхідні знання та навички:

Знати основні правила знаходження похідної функції, з правилами знаходження монотонності функції, зв’язок між похідною та поведінкою функції, поняття критичних точок та точок екстремуму, локального екстремуму, алгоритму знаходження найбільшого і найменшого значення функції. Вміти користуватися комп’ютером, працювати з Інтернетом. Робити висновки. Матеріали та ресурси:

фотоапарат, принтер, засоби для зв’язку з Інтернетом, сканер,

комп’ютер, обладнання для проведення відео конференції.

Друковані матеріали: 

1.     Клепко В.Ю., Голець В.Л.: Вища математика в приклад і задачах. Навчальний посібник. 2-ге видання. – К.: Центр учбової літератури. 2009-594с.

2.     Лисичкин В.Т., Соловейчик И.Л. Математика: Учеб. пособие для техникумов. – М.: Высш.шк., 1991. – 480 с.: ил.

3.     Вища математика: Навч-метод. Посібник для самост. вивч. дисц./ К.Г. Валєєв, І.А. Джалладова, О.І. Лютий та ін. – Вид. 2-ге, перероб. і доп. – К.: КНЕУ, 2002. – 606 с.

4.     Математика: Підручник / О.М. Афанасьєва, Я.С. Бродський, О.Л. Павлов, А.К. Сліпенко. – 2-ге вид., стер. – К.: Вища шк., 2002. – 447 с.: іл.

5.     Рижов Ю.М. Похідна та її застосування. К. Вища школа. 1977

6.     Парно И.К. Производная и её применение к исследованию функций. Москва. Просвещение 1968 Оцінювання знань та вмінь студентів:

Оцінювання проводиться шляхом опитування, спостереження за їх роботою. Оцінювання проводиться викладачем за певними критеріями, з якими студенти ознайомленні до початку роботи над проектом. Ключові слова:

Похідна, монотонність функції, екстремум функції, критичні точки, найбільше і найменше значення функції.

           

 

 

           

 

 

 

           

 

 

 

           

 

 

 

           

 

 

 

 

Хід заняття:

1.     Організаційний етап.

2.     Актуалізація опорних знань. Формулювання теми, мети й завдань уроку. Мотивації навчальної діяльності.

 

Викладач:

Добрий день шановні, вітаю всіх присутніх!

Сьогодні у нас незвичайне заняття. Науково технічний прогрес так швидко крокує в 21 сторіччі, що навіть у нашому коледжі ми зможемо здійснити подорож у часі. Позаду ДПА, ЗНО, навчання у вищих учбових закладах, — як швидко минає час, і ось ви вже молоді наукові співробітники.

Ще у 19ст. математик Пафнутій Львович Чебишев наголошував, що особливу важливість мають ті методи науки, які дозволяють розв’язувати задачу, спільну для всієї практичної діяльності людини:

— як вчинити використовуючи наявні засоби, щоб досягти найбільшої вигоди.

 У наш час з такими проблемами стикаються представники різних спеціальностей: інженери-технологи проектують виробництво так, щоб продукції випускалось як найбільше при найменших затратах; конструктори літальних апаратів розробляють прилади з якомога меншою

масою; економісти намагаються спланувати зв’язки заводу з джерелами сировини

так щоб транспортні витрати були найменші.

У нас сьогодні відкрите засідання наукової ради, тема якого “Застосування похідної до розв’язування прикладних задач”.

Ми розглянемо як можна застосовувати знаходження найбільшого і найменшого значення функції в різних галузях науки.

 На цьому засіданні присутні представники кафедр: історії, біології, економіки, математики та фізики, залізничного транспорту, медицини та філології; представники преси, спостерігачі та фахові консультанти. Перед тим, як розпочати наукову раду пригадаємо 

Алгоритм знаходження найбільшого і найменшого значення функції під час розв’язання прикладних задач:

 Задачі такого типу носять загальну назву – задачі на оптимізацію (від латин. – найкращий).

У найпростіших задачах на оптимізацію маємо справу з двома величинами, одна з яких залежить від іншої, причому необхідно знайти таке значення другої величини, при якому перша досягає свого найменшого або найбільшого значення (найкращого за даних умов). 

Задачі на оптимізацію розв’язують за схемою, що складається з трьох етапів математичного моделювання:

1.                  Складання математичної моделі;

2.                  Робота з моделлю;

3.                  Відповідь на запитання задачі.

І етап. (складання математичної моделі)

1.                   Виділіть величину оптимізації, проаналізувавши умову задачі (величину, про найбільше або найменше значення, якої йде мова). Позначте її буквою у (або S, V, R, t - залежно від умови, змісту).

2.                   Прийміть одну з невідомих величин, які задіяні в задачі, через котру порівняно легко можна виразити величину оптимізації, за незалежну змінну. Позначте її буквою х (або якоюсь іншою). Визначте реальні границі зміни незалежної змінної (відповідно до умов задачі), тобто область визначення Х для шуканої величини оптимізації.

3.                   Виходячи з умови задачі, виразіть у через х. Математична модель являє собою функцію у=f(х) з областю визначення Х, яку знайшли в кроці 2.

           

ІІ етап. (робота з моделлю)

Використовуючи алгоритм, знайдіть у_min або уmax залежно від того, що потрібно в умові задачі, для функції у=f(х), х_Х.

 

ІІІ етап. (відповідь на питання задачі)

Дайте конкретну відповідь на питання задачі, спираючись на результати, отримані на ІІ етапі.

           

НАУКОВА РАДА

 Секретар: Розпочинаємо роботу наукової ради. Зараз важко уявити собі різні галузі життєдіяльності без розв’язування прикладних завдань за допомогою диференціального числення. 

                        Слово надається представнику КАФЕДРИ ІСТОРІЇ.

Перший представник кафедри розповідає легенду « Задача цариці Дідони»

- Цікавою є легенда про відшукання найбільшого значення функції, за якою засновниця м. Карфагена Дідона, дочка царя Тірів, посварившись з братом Пігмаліоном, втекла від свого батька і після багатьох пригод з’явилася на південному узбережжі Середземного моря. Тут, у царя Нарбаса, за невеликі гроші вона купила шматок землі «не більше, ніж можна обміряти шкурою бика» - як зазначалося в угоді. Місцеві жителі вважали умову буквальною і розраховували, що Дідоні для нового поселення дістанеться дуже маленький клаптик узбережжя. Проте спритна Дідона розрізала шкуру бика на найтонші смужки, зв’язала їх мотузкою і, закріпивши один її кінець на березі моря, пішла з іншим вздовж берега. Перед нею постало питання: яку форму потрібно надати мотузці, щоб «обміряти шкурою бика» найбільшу площу? Зокрема це, — є задача на пошук замкненої кривої даної довжини, що обмежує найбільшу площу. Виявляється, що такою кривою є коло. Дідоні, щоб розв’язати задачу, потрібно було обійти півколо з центром у точці О, довжина якого дорівнювала довжині мотузки. Дякую за увагу.

 

Питання преси: Читачі журналу «Знання-сила» цікавляться, звідки пішло диференціальне числення, де його джерела та хто намагався розв’язати перші задачі?

Другий представник КАФЕДРИ ІСТОРІЇ доповнює:

 

До відкриття похідної незалежно один від одного прийшли два відомих вчених – Ісаак Ньютон та Го́тфрид Ви́льгельм Лейбніц наприкінці 17 століття.

 

( слайди презентації «Творці математичного аналізу»)

Ньютон, даючи означення похідної, виходив із задач механіки; Лейбніц – із геометричних задач. Але відкриттю похідної і основ диференціального числення передували роботи таких великих вчених як П’єра Ферма та Рене Декарта.

Хоча сам термін «похідної» і позначення f ^ꞌ(x) ввів Жозеф Лагранж, велику роль у розвитку диференціального числення відіграв Леонард Ейлер.

За допомогою диференціального числення було розв’язано цілий ряд задач теоретичної механіки, фізики та астрономії. Зокрема, вчені передбачили повернення комети Галлея, що стало тріумфом науки 18 століття.

Секретар:

 

Дякуємо представникам КАФЕДРИ ІСТОРІЇ та надаємо слово представникові КАФЕДРИ БІОЛОГІЇ.

 

(слайд КАФЕДРА БІОЛОГІЇ, умова задачі)

 

Представник КАФЕДРИ БІОЛОГІЇ:  В нашій галузі також неможливо уявити відсутність похідної. Доказом цього дана задача:

Задача:

У живильне середовище вносять популяцію з 1000 бактерій. Чисельність популяції зростає за законом р(t)= 1000 + ( 1000t ) ; t- виражається в секун( 100 + t²)

дах. Знайти максимальний розмір цієї популяції. Дана задача розв’язується таким чином:

Розв’язання:

^1000t )1000001000t²

                 Знаходимо похідну функції: p(x)(1000                

                                                                                                                                   100t²                  (100t²)²

Критичні точки: р(t) = 0;==>знаменник не дорівнює нулю, тоді

 1000001000t² 0      

t² 1000                  

Від’ємних секунд не буває, тому t= -10 – сторонній коt1 10        рінь. t2 10       

 

Отже, максимальний розмір цієї популяції через 10 секунд буде рівним р(10)=1050.

           

 

 

( інший представник кафедри розв’язує на дошці задачу, всі записують розв’язок в конспекти, в процесі розв’язування студенти мають право задавати питання).  

 

Секретар: Дякуємо КАФЕДРИ БІОЛОГІЇ. Звісно, не змогли залишитися байдужими молоді МАТЕМАТИКИ ТА ФІЗИКИ 

 

( слайд КАФЕДРА МАТЕМАТИКИ ТА ФІЗИКИ)

Представник кафедри: На нашу кафедру надійшло замовлення підприємця:

Зробити розрахунки на виготовлення консервної банки циліндричної форми об'ємом 1000 см³, щоб витрати жерсті на її виготовлення були мінімальні. Виходячи з цього завдання, ми склали задачу і розв’язали її.

Розв’язання

Площа повної поверхні циліндра S 2RH 2R2 За умовою відомий об’єм циліндра V = 1000 см³. V

                                                 2                           H  2

Формула ^{V R H} , де ^R

                S  2R V  2R2  2V  2R2     S  2000 2R2

       Тоді             R2                                    R               або          R              

2000

S   R₂  4R

Знаходимо похідну:

Знаходимо критичні точки: S  0;

2000

4R  R₂  0

4R³  2000

R³ _ ²⁰⁰⁰ _ ⁵⁰⁰ ; звідси R = 5,4см

4 

2000

        Тоді H  R₂  21,8см.



Отже, при R = 5,4 см і Н = 21,8см витрати жерсті буде найменше.

 

 

           

Інша задача, яка потребує застосування похідної:

 

 

 

 

Дощова крапля падає під дією сили тяжіння, рівномірно випаровуючись так, що її маса змінюється за законом m=1- 2t/3 (де m - в грамах, t -в секундах).Через скільки секунд після початку падіння кінетична енергія краплі буде найбільшою?

Розв’язування

Кінетична енергія знаходиться за формулою: ^Ek ^mv2² , швидкість пада-

ючої дощової краплі під дією сили тяжіння описується формулою: v^v₀  gt , де ^v₀=0.

          Для знаходження найбільшого значення функції зміни кінетичної енергії знаходимо похідну: 

Ek (g2(t22  t33)) g2(2t221  3t331)  g2(t t2)

Прирівнюємо її до нуля і знаходимо критичне значення: g²(t t²)0t(1t)0

 

                                                                        t 0    або   t 1

В час t 0 кінетична енергія ^Ek0, отже кінетична енергія краплі буде найбільшою через 1с.

Секретар: Дякую представникам кафедри МАТЕМАТИКИ ТА ФІЗИКИ.

Виявили бажання й медичні світила нагадати про взаємозв’язок теоретичних пошуків з реальним життям.

           

 

 

(слайд КАФЕДРА МЕДИЦИНИ)

 

Представники кафедри

           

 

Концентрація ліків у крові хворого через деякий час після ін’єкції задається формулою С(t)=16t/(10t+20)². Знайти максимальну концентрацію і час, коли вона досягається. (задача розв’язується на дошці).

 

Розв’язування

За умовою концентрація ліків у крові хворого після ін’єкції задається форму-

16t

лою C(t)  (10t             2

₂₀₎

Для того. Щоб знайти максимальну концентрацію і час, коли вона досягне максимуму, ми знаходимо похідну

                                                                              ²

                             16t           16(10t  20)  2(10t  20)1016t   (10t  20)(160t  320 640t)

C(t)   (10t  20)2               (10t  20)4                                                          (10t  20)4                                     

320 480t

 (10t  20)₃

Прирівнюємо до нуля, знаходимо критичні точки:

320 – 480t = 0;  480t = 320; t = 0,67 с Тоді максимальна концентрація:

С(0,67)    0,015

Секретар: Дякую представникам кафедри. Хто б міг подумати, що пошук найбільшого та найменшого значення функції зможе вирішити й залізничні негаразди. Просимо представників кафедри ЗАЛІЗНИЧНОГО ТРАНСПОРТУ розвіяти наші сумніви. 

 

 

(слайд КАФЕДРА ЗАЛІЗНИЧНОГО ТРАНСПОРТУ)

 

           

 

 

 

До нас звернувся начальник станції Терешкова, у якого вистачає грошей тільки на закладку цоколю підсобно-господарського приміщення, довжиною 60м. При цьому він бажає, щоб площа будинку була найбільшою. За цими вимогами ми склали задачу і розв’язали її, наш замовник залишився задоволеним (задача розв’язується на дошці).

Розв’язування

За умовою, цоколь підсобного господарства повинен мати периметр 60 м.

Тоді довжина l і ширина h буде становити в сумі 30 м.

Нехай довжина l = хм, отже ширина h= (30 - х) м. Площу знаходимо за формулою:

S = l×h =x(30 - x) = 30x – x²

Знайдемо похідну функції S  302x і прирівняємо до нуля. Шукаємо критичну точку.

30 – 2х = 0; х = 15 м.

Отже, довжина l = 15 м і ширина  h=15 м.

Тобто, для того, щоб площа приміщення була найбільшою, потрібно щоб воно було квадратної форми.

           

Секретар: Дякую, представники кафедри ЗАЛІЗНИЧНОГО ТРАНСПОРТУ розвіяли наші сумніви А чим нас здивує КАФЕДРА ЕКОНОМІКИ?

 

 

( слайд КАФЕДРА ЕКОНОМІКИ та умова задачі):

 

Витрати на паливо для тепловоза ділиться на дві частини. Перша із них не залежить від швидкості і дорівнює 480 гривен за годину. А друга частина витрат пропорційна кубу швидкості, причому при швидкості 10 (км за годину) ця

частина витрат дорівнює 30 гривен за годину. Необхідно знайти, при якій швидкості сума витрат на 1 км шляху буде найменшою.     

Розв'язок.

Позначимо через х (км/год) — швидкість тепловоза. Тоді друга частина витрат дорівнює kx³ де k — коефіцієнт пропорційності. Для визначення k підставимо х = 10, тоді: 30 = 1000k , звідки k = 0,03.

1

Тепловоз пройде 1 км шляху за х годин. Витрати на паливо будуть рівні:

          1               ³ 1

480  0,03х  х    ^х .

Необхідно знайти найменше значення функції

1      ² f (x)  480  0,03x на проміжку (0; ∞). x Знайдемо похідну:

1

f (x)  480 ₂  0,06x x

                                                                ³           480

                                                              x     8000

        Якщо ^{f (x)} = 0, то          ^0,06               , а х = 20.

Отже, при х = 20 функція f(х) досягає мінімального значення, тобто при швидкості тепловоза 20 (км за годину) сума витрат на паливо буде найменшою.  (задача розв’язується на дошці).

Секретар: Дякуємо, молодці. Слово надається гуманітаріям, які як завжди приготували щось незвичне.

 

(слайд КАФЕДРА ФІЛОЛОГІЇ)

           

 

 

 

 

Представник кафедри:

 

Перша жінка математик С. В. Ковалевська сказала: 

“Математик повинен бути поетом у душі.”

І, слідуючи її словами, ми на нашому занятті відкриємо літературну сторінку “Графіки функцій – прислів’я”. Підберіть до графіків функцій, зображених на слайдах, прислів’я, які розкривають суть процесів функції. Розглянемо перший графік, які прислів’я вам спадають на думку?

           

 

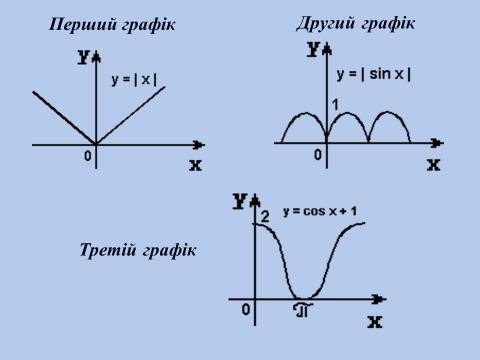 Перший графік.        Другий графік.                         Третій графік.

(студенти називають прислів’я до графіків функцій).

Приклади відповідей:

1)    Хто дбає, той і має. 

Як гукнеться, так і відгукнеться.

З ким поведешся, того і наберешся. 

Як постелиш, так і виспишся.

Яке коріння, таке й насіння. 

За що купив, за те й продав.

Що на умі, то й на язиці.

2)    Любиш кататися, люби и саночки возить.

Щоб піднятися, треба впасти.

         Без лиха, не бува добра.

3)    З вогню, та в полум’я.

Хоч в лоб, хоч по лобові.

Наша пісня гарна - нова, починаєм її знову.

                Секретар: Добре, дякуємо гуманітаріям.                                       

ПРЕСА: (запитує у представників кафедр)

Ø Я б хотів запитати науковців, які висновки вони зробили з сьогоднішнього засідання?

 

Представники кафедр відповідають:

 

1)  Кафедри довели необхідність вивчення даної теми в навчальних закладах.

2)  Переконливо показали застосування похідної при розв’язуванні прикладних задач в різних галузях науки.

3)  Аргументовано переконали присутніх в актуальності математичних знань.

 

Секретар:

 

           

На цьому засідання нашої наукової ради закінчено. Пропоную проект рішення:

 

РІШЕННЯ

НАУКОВОЇ РАДИ

1.     Можна вважати, що дії щодо моделювання процесів дійсності повністю сформовано в студентів, бо вони можуть за умови повної самостійності:

а) перевести задачу на мову математики;

б) сконструювати математичну задачу;

в) виділити провідну математичну ідею;

г) критично осмислити отриманий результат.

2.     Навчальну дію оцінки можна вважати сформованою на цьому етапі, бо студенти:

а) моделюють процеси дійсності;

б) знаходять і виправляють помилки при розв’язуванні задач.

 

           

Підсумок уроку Викладач підбиває підсумок:

 

Перш ніж будь–яке явище природи або процес економічного, сільськогосподарського характеру піддавати математичному вивченню, його необхідно спростити.

Особливістю розглянутих вище задач є те, що вони мають одну й ту саму математичну модель.

Я вважаю, що представники різних кафедр вдало підібрали задачі з галузі щоб продемонструвати методи диференціального числення до розв’язування прикладних задач.

Записуємо домашнє завдання: Повторити пройдений матеріал:

Клепко В.Ю., Голець В.Л.: Вища математика в приклад і задачах ст. 238-344.

 

Заняття закінчено. Бажаю всім успіху. Дякую за роботу.                                        

Після відбулося обговорення проведеного відкритого заняття та заповнення відповідних бланків відвідування заняття: