Конспект уроку на тему "Геометрична прогресія".

Тема уроку. Формула n-го члена геометричної прогресії.

Мета уроку:

• виховувати культуру усного та писемного мовлення та міжособистісного спілкування;
• закріпити знання учнів про зміст означення та супутних понять геометричної прогресії, а також про її основні властивості; доповнити ці знання знанням формули п-го члена геометричної прогресії; сформувати вміння записувати формулу п-го члена геометричної прогресії, а також розв'язувати різні за змістом задачі на викорис­тання цієї формули;
• розвивати активність, уважність, спостережливість.

Тип уроку: комбінований.

Обладнання: опорний конспект.

Хід уроку

І. Організаційний етап
Перевіряю готовність учнів до уроку, налаштовую їх на роботу.

IІ. Повідомлення теми, мети і задач уроку

Так само, як при вивченні питання про формулу п-го члена арифметичної прогресії, роботу на цьому етапі уроку організуємо як колективний пошук розв'язання задачі: як найраціональнішим способом знайти значення n-го члена геометричної прогресії, зна­ючи її перший член і знаменник.

Усвідомивши нераціональність розв'язування задачі відомим учням способом (через застосування рекурентної формули), вони приходять до запитання: чи не існує способу знаходження будь-якого члена геометричної прогресії без необхідності знаходити попередні кілька її членів? Пошук відповіді на це запитання — основна мета уроку.

ІІІ. Відтворення основних положень вивченого на попередньому уроці

1.  Перевірка домашнього завдання

Вибірково перевіряю зошити, відповідаю на питання, що виникли у учнів під час виконання домашнього завдання.

Побудова теплиці.

Потрібно виготовити вертикальні стержні для теплиці з дроту так, щоб найменший мав довжину 5 м, а кожний наступний був на 2 м довший (до 7 стержня). Обчисліть довжину дроту, необхідну для виготовлення стержнів.

Розв'язання:

Маємо арифметичну прогресію (), де .

(м) 

ІV. Доповнення знань

План вивчення нового матеріалу

1. Формула n-го члена геометричної прогресії.
2. Приклади застосування виведеної формули

Опорний конспект

V. Відпрацювання вмінь

Письмові вправи

Зміст письмових вправ уроку може бути таким:

1. задачі на пряме застосування формули п-го члена геометричної прогресії, у якої задано перший член та знаменник або яка задана переліком перших кількох своїх членів:  Розминка 1, завдання 2 ст 249.
2. знайти номер деякого члена геометричної прогресії або пере­вірити, чи є дане число членом даної геометричної прогресії: Розминка 2, завдання 1 ст 250. Тренуємось завдання 1, ст. 251.

А зараз трішки розвантажемося.

Психологічне розвантаження.

        У вас на партах лежать картки, на яких записані цифри від 1 до 9. Зараз зафарбуйте цей ряд двома різними кольорами у будь – якому порядку.

             1, 3, 6, 7, 9;    2, 4, 5, 8. 

  А доки ви зафарбовуєте, я розповім вам про чудового математика на прізвище – Рамсей, який жив  на початку ХХ століття.

Він заснував теорію, яка стверджувала, що у світі немає абсолютного безладу. Навіть, здавалося б, саме неупорядкована система має визначені математичні закономірності.

Згадайте, коли ви дивитесь на зірки, то може здаватися, що вони розміщені у хаотичному порядку. Але ще в давнину люди помітили там сузір’я Риб і Касіопеї, Лева і Оріона. І на ваших картках, здається , що цифри зафарбовані у випадковому порядку. Але Рамсей стверджував, що це не так, довівши слідуючий факт: зверніть увагу, що хоча б 3 числа одного кольору складають арифметичну прогресію. Запишіть ці числа.

Розумова розминка.(учні розв’язують кросворд)

По вертикалі: 1.Послідовність, у якій кожний наступний член менший за попередній.

2.Послідовність чисел, у якій кожний член. починаючи з другого, утворюється множенням попереднього на стале число.

 3. Нескінченна або скінченна сукупність чисел.

 4.Слово „прогресія” у перекладі з латинської означає „рух вперед” або...

5. Знаменник геометричної прогресії -3; -9; -27; -81;... дорівнює...

6. Стале число, множенням на яке утворюється кожний наступний член геометричної прогресії.

7.Різниця арифметичної прогресії 15,21, 27,...33,...

8. Число, додаванням якого утворюється кожне наступне число у арифметичній прогресії.

 9. Термін „прогресія” вперше зустрічається у римського автора Боеція у... столітті. 10. По горизонталі ви прочитаєте слово...

Відповіді. 1. Спадна. 2. Геометрична. 3.Послідовність. 4.Прогрес. 5. Три. 6. Знаменник. 7.Шість. 8.Різниця. 9.П'яте.

Тестові завдання

1. Яка з наведених послідовностей є геометричною прогресією?
   а) 2; 6; 18; 54;  б) 80; 40; 20; 5; в) 4; 8; 32; 64;  г) 2; -10; 50; 250.
2. Знайдіть знаменник геометричної прогресії (b_п), якщо b₂ = -36, b₃ = 4.

а)9;   б)-9;   в)1/9;   г)-1/9.

3. Послідовність (с_п) - геометрична прогресія, с₂ = 16, с₄ = 4. Знайдіть с_3.

а)8;                       б) 2;                       в) 64;                       г) ±8.

4. Знайдіть знаменник геометричної прогресії (b_п), якщо b₅ = 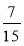, b₆ = .

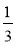а) ;   б) ;   в) ;   г) .

5. Дев'ятий член геометричної прогресії дорівнює 12, а знаменник
   дорівнює 3. Знайдіть десятий член геометричної прогресії.

а) 15;   б) 36;   в)4;   г)9.

Цікаві задачі

Задача 1. У газеті, що була виданау1914р., описувалася справа, яка відбулася у місті Новочеркаську, про продаж отари, що має 20 овець, за такими умовами: за першу вівцю слід заплатити 1 к., за другу - 2 к., за третю - 4 к. і т. д. У яку суму обійдеться вся отара?

Розв'язання:

1;2; 4; 8;... - геометрична прогресія,

.

=1084575=11000 (крб.).

Задача 2. брудних рук.

Бактерія, потрапивши в організмлюдини, до кінця 20-ї хвилини ділиться на 2, кожна з них через 20 хвще на дві і т.д. Скільки бактерій стане в організмі людини через добу?

Розв’язання. Слайд 31.

1доба=24год.; 24год.=1440хв.; 1440:20=72

За умовою задачі отримаємо геометричну прогресію:

1;2;4;8;…;

b₁=1, q=2

S_n=((b₁(qⁿ-1)):q-1)=((1*(2⁷² -1)):1)= 2⁷² - 1≈ 2⁷²(бактерії)

Відповідь: в організмі за добу буде 2⁷² бактерій.

VI. Підсумки уроку

Контрольні запитання

1. Як знайти знаменник геометричної прогресії, якщо відомі її перший і другий члени?
2. Як знайти третій член геометричної прогресії, якщо відомі її перший і другий члени?
3. Як знайти шостий член геометричної прогресії, якщо відомі її перший член і знаменник?

VII. Домашнє завдання

1. Вивчитипараграф 19.
2. Виконати  №1 ст 259.