Конспект уроку на тему " Мішані числа"
Тема: Мішані числа
Мета: - навчальна: ознайомити учнів з поняттям мішаного числа; формувати вміння виділяти цілу частину з неправильного дробу і перетворювати мішане число у неправильний дріб; навчитися застосовувати алгоритми під час розв’язування вправ.
- розвивальна: розвивати вміння логічно обґрунтовувати свої думки; пам’ять, увагу, уміння працювати в групі.
- виховна: виховувати самостійність, взаємодопомогу, наполегливість, толерантність.
Тип уроку: урок засвоєння нових знань
Обладнання: мультимедійна дошка, презентація
План уроку
- Організаційний етап, перевірка домашнього завдання ( 2 хв)
- Актуалізація опорних знань (10 хв)
- Формулювання мети і завдань уроку (5 хв)
- Засвоєння знань (20 хв)
- Узагальнення і систематизація.(5 хв)
- Підсумки уроку ( 2 хв)
- Домашнє завдання ( 1 хв)
Хід уроку
- Організаційний етап, перевірка домашнього завдання
Привітання. Перевірка готовності учнів до уроку. Перевіка домашнього завдання
( Підручник за 5клас » Математика Автор: Мерзляк, Полонський, Якір, 2018)
Три учня біля дошки розв’язують. Всі слідкують і перевіряють
№763(1,3,6)
-
5 : 7 =
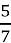 3) 1 : 6 =
3) 1 : 6 =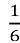 6) 12 : 39 =
6) 12 : 39 = 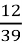
№765
![]() = 5 : 7 2)
= 5 : 7 2) ![]() = 3 : 10 3)
= 3 : 10 3) ![]() = 29 : 5
= 29 : 5
№767
-
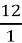 2)
2) 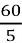 3)
3) 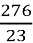
- Актуалізація опорних знань
Математичний диктант
Учні отримують аркуші паперу, на яких виконують завдання математичного диктанту. Після виконання обмінюються аркушами, і виконують взаємоперевірку, спираючись на «слайди з відповідями» , ставляють оцінку.
- Число записане над рискою дробу називають…? (Чисельник)
- Дріб, у якого чисельник менший від знаменника, називається…? (Правильний)
-
Як записати частку 17 : 4 у вигляді дробу? (
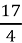 )
)
-
Які із заданих дробів:
 ;
; 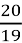 ;
; 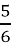 ;
; 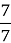 ;
;  неправильні? (
неправильні? (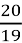 )
)
-
Який із наведених вище дробів дорівнює натуральному числу?(
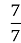 )
)
- Що означає дробова риска у записі дробу?( Ділення)
Гра «Знайди відповідність»
Онлайн разом з вчителем учні виконують завдання
https://naurok.com.ua/test/pravilni-i-nepravilni-drobi-mishani-chisla-750984/match
Фізкультхвилинка
- Формулювання мети і завдань уроку
Ви вже вивчили натуральні числа, знаєте що існують дробові числа. Але в житті зустрічаються ситуації коли ви маєте справу одночасно і з натуральними числами та дробами. Ви можете виразити в метрах 6 см, у годинах 18 хв і т.д . А як виразити в кілограмах 6 кг і 100 г, в гривнях – 15 грн. 20 коп?
Тема нашого уроку « Мішані числа»
Сьогодні на уроці ви дізнаєтесь яке це мішане число та навчитеся виділяти цілу частину з неправильного дробу і перетворювати мішане число у неправильний дріб.
- Засвоєння знань
Число ![]() можна записати у вигляді суми двох дробів, наприклад, так :
можна записати у вигляді суми двох дробів, наприклад, так :
![]() =
= ![]() . Оскільки
. Оскільки ![]()
![]() +
+ ![]() = 2 +
= 2 +![]()
Аналогічно можна записати : ![]() =
= ![]() =
= ![]() +
+ ![]() = 4 +
= 4 + ![]() .
.
Кожний із неправильних дробів ![]() ми записали у вигляді суми натурального числа і правильного дробу.
ми записали у вигляді суми натурального числа і правильного дробу.
Так можна записати будь-який неправильний дріб, чисельник якого не ділиться націло на знаменник.
Такі суми, як 2 +![]() 4 +
4 + ![]() , прийнято записувати більш коротко:
, прийнято записувати більш коротко:
2 +![]() =2
=2![]() 4 +
4 + ![]() =4
=4 ![]() . Число 2
. Число 2![]() читають: « дві цілих п’ять сьомих»,
читають: « дві цілих п’ять сьомих»,
Число 4 ![]() читають: « чотири цілих одна п’ята».
читають: « чотири цілих одна п’ята».
Число 2![]() називають мішаним числом. У мішаному числі 2
називають мішаним числом. У мішаному числі 2![]() натуральне число 2 називають цілою частиною мішаного числа, а дріб
натуральне число 2 називають цілою частиною мішаного числа, а дріб ![]() – його дробовою частиною.
– його дробовою частиною.
Дробова частина мішаного числа є правильним дробом.
Навчимося записувати неправильний дріб у вигляді мішаного числа, тобто виділяти його цілу і дробову частину.
Розглянемо, наприклад, число ![]() . Маємо:
. Маємо:
![]() =
=![]() =
=![]() +
+ ![]() = 4 +
= 4 + ![]() = 4
= 4 ![]()
Щоб неправильний дріб, чисельник якого не ділиться націло на знаменник, перетворити в мішане число, треба чисельник поділити на знаменник; отриману неповну частку записати як цілу частину мішаного числа, а остачу – як чисельник його дробової частини.
Будь-який неправильний дріб, чисельник якого не ділиться націло на знаменник, можна подати у вигляді мішаного числа.
Приклад 1. Перетворіть неправильний дріб ![]() у мішане число.
у мішане число.
Розв’язання: Поділимо чисельник дробу на знаменник.
![]()
![]()
![]() 212 13
212 13
![]() 13 16
13 16
![]() 82
82
![]() 78
78
4
Неповна частка – 16 це ціла частина числа, а остача 4 –чисельник дробової частки . Отже, ![]() = 16
= 16 ![]()
Щоб перетворити мішане число в неправильний дріб, треба цілу частину помножити на знаменник дробової частини та до отриманого добутку додати чисельник дробової частини; цю суму записати як чисельник неправильного дробу, а в його знаменнику записати знаменник дробової частини мішаного числа
Приклад 2 Запишіть число 7 ![]() у вигляді неправильного дробу.
у вигляді неправильного дробу.
7 ![]() = 7 +
= 7 + ![]() =
= ![]() =
= ![]() =
= ![]()
Щоб знайти суму двох мішаних чисел, треба окремо додати їхні цілі та дробові частини.
Приклад 3. Виконайте додавання 3 ![]() + 5
+ 5 ![]()
3 ![]() + 5
+ 5 ![]() = 8 +
= 8 + ![]() =8 +1
=8 +1![]() = 9
= 9![]()
Щоб знайти різницю двох мішаних чисел, треба від цілої та дробової частини зменшуваного відняти відповідно цілу та дробову частину від’ємника.
Приклад 4. Виконайте віднімання 8 ![]() - 6
- 6 ![]()
-
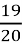 - 6
- 6 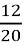 = (8 -6) +(
= (8 -6) +(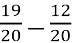 ) = 2 +
) = 2 + 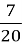 =2
=2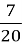
I V. Узагальнення і систематизація
Дайте відповідь на такі запитання:
- Наведіть приклад неправильного дробу.
- Які дроби можна записати мішаним числом?
- Яке число називають мішаним?
V.Підсумки уроку
Що нового дізналися на уроці?
Чим вам сподобався цей урок?
Чим запам’ятався?
VI.Домашнє завдання
П.29 чит. Вивчити правила.
№773(1,2)
-
 =2
=2  2.
2. 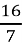 = 2
= 2 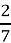
№777(1,2)
-
2
 =
=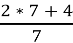
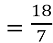 2. 3
2. 3 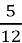 =
= 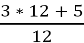 =
= 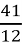
Для учнів ( пояснення матеріалу уроку) https://www.youtube.com/watch?v=uruuCZrW9_s&ab_channel=%D0%92%D0%B8%D0%BA%D1%82%D0%BE%D1%80%D0%B8%D1%8F%D0%9F%D0%BE%D0%B4%D0%BA%D0%BE%D0%BB%D0%B7%D0%B8%D0%BD%D0%B0


про публікацію авторської розробки
Додати розробку
