Тема.   Подібність трикутників

Мета: формувати в учнів уявлення про подібні трикутники, вміння застосовувати означення подібних трикутників при розв’язуванні задач; розвивати вміння аналізувати, культуру усного мовлення та пізнавальний інтерес до математики.

Тип уроку: засвоєння нових знань, умінь.

Хід уроку

І. Організаційний етап

Вступне слово вчителя.

Чудова геометрична фігура і найпопулярніша в шкільній програмі по геометрії – це трикутник – одна з перших геометричних фігур, про властивості якої людство дізналося ще в давнину.

Може ви думаєте, що трикутники «оселилися» лише на сторінках підручника  геометрії і більше їх ніде не побачити?

ІІ. Перевірка домашнього завдання

Сьогодні про це нам розкажуть ваші однокласники, які проведуть для вас віртуальну екскурсію  «В світі трикутників».

       1. Правило «золотого трикутника» засноване на психології покупця : знайшовши в магазині потрібний йому товар, покупець придбавши його прямує до каси. Завдання продавця : змусити його затриматися в приміщенні як можна довше. Для цього він (продавець) розташовує самий ходовий товар у вершинах уявного трикутника ( у різних кінцях магазину), саме для того, щоб змусити покупця пройти весь периметр магазину, а отже затриматись як можна довше у ньому. Чим більша площа трикутника між входом, касовим вузлом і ходовим товаром тим більш вдалим можна назвати планування  магазину, тим більшим є об’єм продажу.

2. Починаючи гру в більярд, необхідно розташувати кулі у вигляді трикутника. Для цього використовують спеціальне пристосування.

Кеглі при грі Боулінг теж розташовують у вигляді рівностороннього трикутника. 

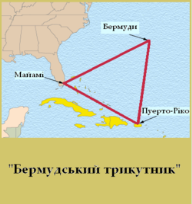2. Бермудський трикутник інколи називають ще диявольським трикутником. Це район в Атлантичному океані, в якому відбувається нібито таємничі зникнення морських і повітряних суден. Район, обмежений лініями від Флориди до Бермудських островів, далі до Пуерто-Ріко і назад до Флориди через Багами, нагадує собою трикутник. Висуваються різні гіпотези для пояснення цих зникнень, від незвичайних погодних явищ до викрадення інопланетянами.

4.   В 1934 році Оскар Реутерсвард створив перший неможливий трикутник, складений з серії кубиків. Хоча багато художників створювали неможливі фігури, саме Реутерсвард відкрив новий світ фантазій. З тихий пір Реутерсвард створив тисячі неможливих фігур. В 1980 році Шведський уряд вирішив розмістити неможливий трикутник, а також дві інші фігури Реутерсварда,  на поштових марках,  які випускалися з 1982 долі приблизно два роки.             

В  1954  році  Роджер  Пенроуз  після лекції  голландського

графіка М. К. Ешера відкрив заново неможливий трикутник і намалював його в іншій формі. На відміну від трикутника Реутерсварда, трикутник Пенроуза намальований з використанням лінійної (а не паралельною, як в Реутерсварда) перспективи, що додає йому більше неможливості. Слід врахувати, що Роджер Пенроуз не був знайомий з роботами Реутерсварда та інших.

Трикутник Пенроуза надихає художників і скульпторів.

ІІІ. Актуалізація опорних знань та вмінь.

Виконання усних вправ

З метою успішного засвоєння учнями змісту нового матеріалу уроку необхідно активізувати їх знання  про:

• пропорційні відрізки;
• теорему Фалеса;
• відношення двох відрізків;
• теорему про пропорційні відрізки.

Виконання письмових вправ

№1.                                 

                    На рисунку DМ || ВС,

   АD = 6см,  АМ = 8см,

      АВ  = 36см

                                                                                                                                                                                                        Знайти МС.                                                 

ІV. Формулювання мети і завдань уроку, мотивація навчальної діяльності

В повсякденному житті часто зустрічаються речі, які мають однакову форму, але різні розміри. В навколишньому світі багато предметів які ми порівнюємо між собою, знаходимо подібності та відмінності між ними. Краще розбиратися в цьому нам допоможе вивчення теми «Подібність».

V. Сприйняття та усвідомлення нового матеріалу

План вивчення нового матеріалу

1. Подібні фігури.
2. Означення подібних трикутників.
3. Коефіцієнт подібності.
4. Лема про подібні трикутники.
5. Властивості подібних трикутників.

Геометричні фігури, які мають однакову форму, називають подібними.

Наведіть приклади подібних фігур з навколишнього світу.

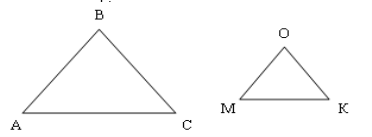
Означення. Два трикутники називаються подібними, якщо сторони одного трикутника відповідно пропорційні сторонам другого трикутника та їхні відповідні кути рівні.

Число k, яке дорівнює відношенню відповідних сторін подібних трикутників, називають коефіцієнтом подібності.

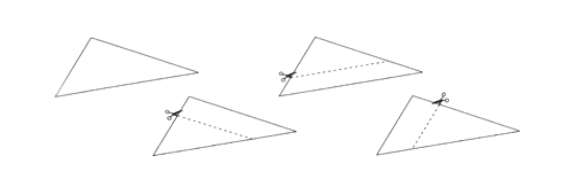 Практична робота.

1. Виріжте з паперу чотири рівні трикутники.

2. Один з них залиште без змін, а від інших відріжте частини, що відтинаються прямими, паралельними кожній зі сторін.

3. Порівняйте кути трьох отриманих трикутників із кутами першого три­кутника. Зробіть висновок.
4. Виміряйте довжини сторін двох утворених трикутників.

Порівняйте відношення довжин їх відповідних сторін. Зробіть висновок.

    Лема. Пряма, яка паралельна стороні трикутника і перетинає дві інші його сторони, відтинає від даного трикутника йому подібний.

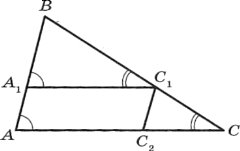Доведення.

В ∆АВС А₁С₁ ‌|| АС.  Доведемо,  що  ∆АВС ~  ∆А₁ВС₁. В трикутниках А = =А₁, С = С₁  як відповідні при паралельних прямих  АС  і  А₁С₁    та   січних   АВ  і  ВС  відповідно, В спільний. Отже, кути трикутників  рівні. За теоремою про пропорційні відрізки = . Звідки =.                                                                            

Проведемо С₁С₂ || АВ.  За  тією  ж  теоремою отримуємо,  що  .  Очевидно,  що   АА₁С₁С – паралелограм.  Тоді А₁С₁ = АС₂.                                                                         

Звідки ,  тоді . Отже, відповідні  сторони,  пропорційні.   Тому   за   означенням ∆АВС ~ ∆А₁ВС₁. 

Властивості подібних трикутників.              

1. Відношення периметрів, медіан, бісектрис, висот, радіусів вписаних і описаних кіл подібних трикутників дорівнює коефіцієнту подібності.

2.  Відношення площ  подібних трикутників  дорівнює квадрату коефіцієнта подібності.

VІ. Закріплення та осмислення нового матеріалу

Виконання усних вправ

1. Вкажіть види трикутників, які завжди подібні.
2. Чи можуть бути подібними прямокутний і тупокутний трикутники?
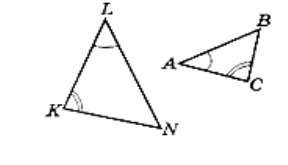3. На рисунку зображено  подібні  трикутники АВС і LNK,  рівні   кути  яких позначено  однаковою  кількістю  дуг.  Які сторони пропорційні?

4. ∆АВС ~ ∆МРО  з  коефіцієнтом

    подібності  0,5.  АВ = 3см,  ВС =

     = 4см,   АС = 5см.  Знайти:

1) сторони ∆МРО;    2) відношення площ подібних трикутників.

5. У рівносторонньому трикутнику провели всі середні лінії. Скільки подібних трикутників утворилось?

Виконання письмових вправ

№2.Сторони трикутника відносяться, як 8 : 6 : 5. Знайти сторони трикутника, подібного даному, якщо: 1) найменша сторона дорівнює 30см; 2) периметр дорівнює 57см.                                     

№3. Сторони трикутника  відносяться як 5 : 4 : 2. Знайти сторони подібного трикутника, якщо сума найбільшої і найменшої сторони 21см.

№4.Два кола з центрами О₁ і О₂ і радіусами 12см і 8см   відповідно мають зовнішній дотик у точці К. Їх спільна зовнішня дотична перетинає пряму О₁О₂ у точці В. Знайдіть відстані від точки В до центрів даних кіл.

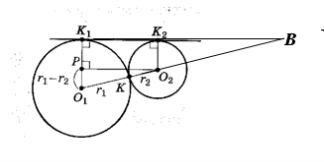Розв’язання.

    Дотична  К₁К₂  перетинає  пряму  О₁О₂ в точці В.  Знайдемо                            

ВО₁  і  ВО₂.

    Так  як О₁К₁ і О₂К₂  радіуси, то    О₁К₁ ⊥ ВК₁  і  О₂К₂ ⊥ ВК₁.  Тоді   О₁К₁ || О₂К₂.   За лемою ∆ВО₂К₂ ~ 

~ ∆ВО₁К_1.  Отже, .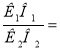

Нехай  ВО₂ = х. Тоді 12 : 8 = ( х +20 ) : х; х = 40. Отже,  ВО₂ = 40см,  а ВО₁ = 60см.

Відповідь: 40см і 60см.

№5. Продовження бічних сторін АВ і СD трапеції АВСD перетинаються в точці К. Знайдіть СК, якщо DК дорівнює 40см, а   ВС : АD = 4 : 5.

Логічна вправа

Яка фігура на рисунку немає властивості, що є в інших фігур?

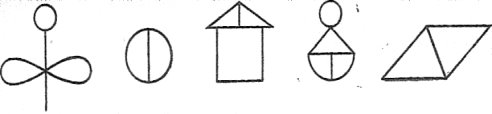
Остання, бо вона не має вертикальних ліній.

VІІ. Підсумки уроку

Контрольні запитання

1. Що являє собою фігура, яка подібна трапеції?
2. Чи подібні два трикутника, якщо сторони одного 4см, 5см, 6см, а другого 8мм, 10мм, 14мм?
3. Чи подібні рівні трикутники?

4.  Чи будуть подібними дві банки ємкістю 3л і 1л?

VІІІ. Домашнє завдання

Вивчити зміст засвоєних на уроці понять.

№1.

       Перша група.

Довести, що відношення периметрів подібних трикутників дорівнює коефіцієнту подібності.

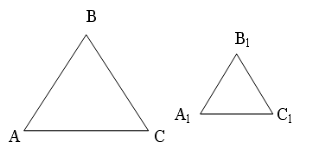Доведення.

Якщо ∆АВС ~ ∆А₁В₁С₁  доведемо, що Р : Р₁ = k.

 Із подібності трикутників           

маємо: , то  ВА = kВ₁А₁; ВС = kВ₁С₁; АС =   = kА₁С₁.  Тоді  Р₁ =  (В₁А₁ + В₁С₁ + А₁С ) · k.   Отже,   Р : Р₁ =  k ×               ×  ( В₁А₁+ В₁С₁ + А₁С₁ ) : ( В₁А₁+ В₁С₁ + А₁С₁ ) =  k .

       Друга група.   

Довести, що відношення площ  подібних трикутників  дорівнює квадрату коефіцієнта подібності.

Доведення.

Якщо ∆АВС ~ ∆А₁ВС₁  доведемо, що S : S₁ = k².

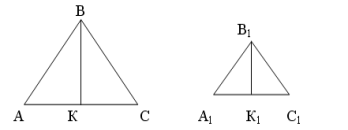Проведемо в ∆АВС і ∆А₁В₁С₁ висоти ВК і В₁К₁. За властивістю подібності ВК : В₁К₁ = АС : А₁С₁ =   k.   Звідси  маємо ВК = kВ₁К₁, АС  = kА₁С₁.  Тоді  S : S₁ =              = ( ½ВК ∙ АС ) : ( ½В₁К₁ ∙ А₁С₁) =  ( ½ kВ₁К₁∙ kА₁С₁) : (½В₁К₁ ∙ А₁С₁ ) = =  k². 

№2.  Діагональ  АС  ділить  трапецію АВСD  ( АD || ВС )  на  два

подібних   трикутники АВС і АСD. Знайдіть АС, якщо АВ = 4см,    АD = 9см.

                                                    Розв’язання.             

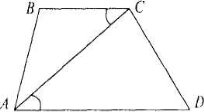За умовою в трапеції АВСD ( АD || ВС ) ∆АВС ~ ∆АСD, то ВАС = САD, АВС =  = АСD, ВСА = СDА. Оскільки ВСА = =САD як внутрішні різносторонні, то ∆АВС рівнобедрений. Отже АВ = ВС. Аналогічно можна довести, що ∆АСD рівнобедрений. Отже, АС = СD. За означенням подібних трикутників ВС : СD =         = АС : АD;  4 : АС =  АС : 9; АС² = 36; АС = 6см.

Відповідь: 6см.