Тема.  Ознака подібності трикутників за двома кутами

Мета: довести ознаку подібності трикутників за двома кутами; формувати вміння застосовувати цю ознаку до розв’язування задач; дослідити умови подібності різних трикутників; розвивати дослідницькі навички, культуру усного мовлення та пізнавальний інтерес до математики.

Тип уроку: засвоєння нових знань, умінь.

 

Хід уроку

 

І. Організаційний етап

ІІ. Перевірка домашнього завдання

Виконання усних вправ

    “ Незрівнянна подібність ”

Запитання.

1. Що ви можете розповісти про  подібність?

2. Наведіть  приклади  подібних фігур, використовуючи  зображення  на  картині.

3. Які  трикутники  називаються подібними?

4. Чи є подібними зображені на картині прямокутні трикутники, катети яких мають довжину 1см?

5. Які властивості подібних трикутників ви знаєте?

6. Як можна визначити коефіцієнт подібності, знаючи довжини висот трикутників?

7. Що ще ми можемо дізнатися, знаючи коефіцієнт подібності? Як?

8. Що нагадує забарвлення равлика? Які ви знаєте “підказки”, аби запам'ятати кольори веселки? 

9. Що загального між нашим равликом  і равликом Паскаля? 

 ( Додаткове завдання дослідницького характеру ).

Перевірка правильності виконання домашнього завдання шляхом пояснення розв’язання по заздалегідь підготовленим рисункам.

 

 

 

 

Виконання письмових вправ

№1. Периметри подібних трикутників відносяться як 5 : 7, а сума їх площ дорівнює 296см². Знайти площі трикутників.

Розв’язання.

Нехай Р₁ і Р₂ – периметри двох подібних трикутників, а S₁ і S₂ – їх площі. Р₁ : Р₂ = 5 : 7 = k, де k – коефіцієнт подібності. Тоді S₁ : S₂ =     = k² = 25 : 49. За умовою задачі S₁ + S₂ = 296. Маємо систему

Розв’яжемо перше рівняння системи.

25S₂ = 49(296 – S₂);

S₂ = 196;  S₁ = 296 – 196 = 100.

Відповідь: 196см² і 100см².

 

ІІІ. Актуалізація опорних знань та вмінь.

Виконання усних вправ

 

1. Якщо АВ ∙ СD = МН ∙ РК, то РК : СВ = ?
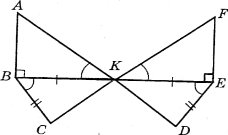2. Користуючись рисунком, вкажіть рівні трикутники й поясніть, чому вони рівні?

 

 

 

 

 

 

ІV. Формулювання мети і завдань уроку, мотивація навчальної діяльності

Ознаки подібності трикутників грають важливу роль в житті людей, зокрема, вони можуть бути використані для проведення різних вимірювальних робіт на місцевості. Але щоб успішно застосовувати ці ознаки при розв’язанні завдань, ми повинні їх знати. Сьогоднішній урок буде присвячений першій ознаці подібності трикутників.

 

V. Сприйняття та усвідомлення нового матеріалу

План вивчення нового матеріалу

1. Друга ознака рівності трикутників.
2. Теорема (перша ознака подібності три­кутників: за двома кутами) формулювання та доведення.
3. Теми для самостійного дослідження.

Чи є аналогія між рівністю і подібністю трикутників, адже за означенням рівні трикутники подібні? Розглянемо другу ознаку рівності і першу ознаку подібності.

 

 

 ІІ ознака рівності                         І ознака подібності

 

 

 

 

 

 

 

 

 

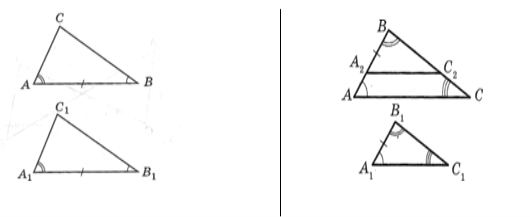
ЯкщоА =А₁, В =В₁ і             Якщо А =А₁, В =В₁ ,

АВ = А₁В_1, то ∆АВС = ∆А₁В₁С₁.   то ∆АВС ~ ∆А₁В₁С₁.

Деяка аналогія існує.

 Теорема  (перша ознака подібності три­кутників: за двома кутами). Якщо два кути одно­го трикутника дорівнюють двом кутам другого трикутника, то такі трикутники подібні.

Доведення.

Розглянемо  ∆АВС і ∆А₁В₁С₁, у яких А =А₁, В =В₁.

Якщо АВ = А₁В₁, то ∆АВС = ∆А₁В₁С₁ за другою ознакою рівності трикутників, а отже, ці трикутники подібні. Нехай, наприклад,        АВ > А₁В₁. Відкладемо на стороні ВА відрізок ВА₂, який дорівнює стороні В₁А₁. Через точку А₂ проведемо пря­му А₂С₂, паралельну стороні АС.

ВАС і ВА₂С₂ є відповідними при паралельних пря­мих А₂С₂ і АС та січній АВ, то ВАС = ВА₂С₂. Тоді ∆А₂ВС₂ = ∆А₁В₁С₁ за другою ознакою рівності трикутників. За лемою про подібні трикутники  ∆А₂ВС₂ ~ ∆ABC. Отже, ∆АВС ~ ∆А₁В₁С₁.

 

Теми для самостійного дослідження.

1. Сформулюйте ознаки подібності рівнобедрених трикутників, виходячи з ознаки подібності трикутників за двома кутами.
2. Сформулюйте ознаку подібності прямокутних трикутників, виходячи з ознаки подібності трикутників за двома кутами.

 

VІ. Закріплення та осмислення нового матеріалу

Виконання усних вправ

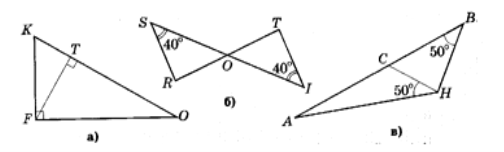Знайдіть пари подібних трикутників та доведіть їх подібність.

 

 

 

 

        

Виконання письмових вправ

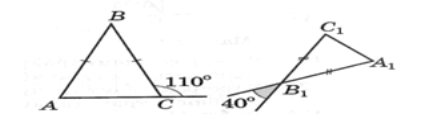
№2. Доведіть подібність ∆АВС і ∆КМО.

                           

 

 

 

 

 

Фізхвилинка.

– Як тренажер нам сьогодні послужить знак подібності (вчитель демонструє плакат із змальованим на нім знаком подібності).

– Пройдіть очима по знаку подібності.

– Закрийте очі.

– Розслабте м'язи лоба.

– Повільно переведіть очні яблука в крайнє ліве положення.

– Відчуйте напругу очних м'язів.

– Зафіксуйте положення.

– Тепер повільно з напругою переведіть очі управо.

– Повторите чотири рази.

– Розплющте очі.

– Пройдіть очима по знаку подібності.

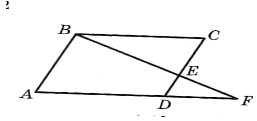№3. На стороні СD паралелограма  АВСD  позначено  точку  Е,  прямі  ВЕ і  АD  перетинаються в точці F,  СЕ = 8см, DЕ = 4см, ВЕ = 10см, АD = = 9см. Знайдіть відрізки ЕF і FD.                                                                                                   

 

 

№4. У  трапеції АВСD ( АD || ВС ) АD = 12см, ВС = 3см, АС =     = 10см. Знайти довжину відрізків АО і ОС, де точка О – точка перетину діагоналей.

 

 

Розв’язання.

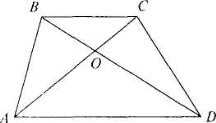Розглянемо ∆ВСО і ∆АОD. В трикутниках   ∠ВОС =∠АОD як вертикальні, а ∠ВОС = ∠ОАD  як  внутрішні різносторонні. Тоді ∆ВСО = ∆АОD за двома кутами.  Звідси ВС : АD = СО : АО. Нехай СО = х, тоді АО = 10 – х. Маємо пропорцію 3 : 12 = х : (10 – х); х = 2. Отже, СО = 2см, АО = 8см.

        Відповідь: 2см і 8см.                             

 

VІІ. Підсумки уроку

Сформулювати ознаку подібності за двома кутами.

В якому з наведених випадків ∆АВС ~ ∆МНК?

1. А =30°, В=50°, 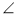М=60°, 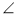К=100°.
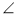2. А=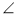С=20°, Н=140°, М=К.

     Таким чином, для того, щоб довести, що трикутники подібні, достатньо знати дві пари елементів трикутників. Зокрема, два кути.          

 

VІІІ. Домашнє завдання

Вивчити зміст засвоєних на уроці понять.

№1. Периметр паралелограма 70см, а його висоти — 3см і 4см. Знайдіть сторони паралелограма.

 

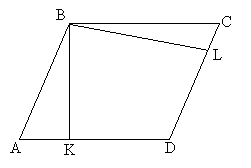                                                                   Розв’язання.

1.    Довести подібність ∆АВК і ∆ВСL.
2.    Знайти коефіцієнт подібності? ( k = ¾ )
3.    Знайти чому дорівнює сума основ. (АВ+ВС=35см)
4.    Яке  рівняння отримали?                  ((35–х):х=3:4)
5.    Відповіді. (15см і 20см)

 

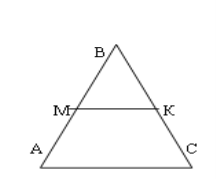
№2.Основи трапеції дорівнюють 8см і 12см. Бічні сторони, рівні 4,5см і 5,2см, продовжені до перетину в точці М. Знайдіть відстані від точки М до кінців меншої основи.

                                                        

Розв’язання.

1. Яка фігура утвориться?

2. Чому дорівнюють  основи   і  бічні                                                                                                                           сторони  трапеції (АМ = 4,5см, КС = 5,2см,  АС =  12см, МК = 8см)?             

3. Довести подібність ∆АВС і  ∆МВК.

4. Знайти коефіцієнт подібності ( k = ⅔ ).

5. Які пропорції утворились (х: (х + 4,5) =  = 2 : 3 і  у : (у + 5,2) = 2 : 3).                             

6. Відповіді ( МВ = 9см і ВК = 10,4см ).