Матеріал до уроку."Використання формул половинного та кратних аргументів"

Матеріал до уроку.

Використання формул половинного та кратних аргументів

Підстановка буде ефективною при спрощенні виразів, які містять у собі складові вигляду, що безпосередньо випливає із формул для тригонометричних функцій подвійного аргументів

Приклад 1. Розв’язати рівняння

Розв’язання. Знаходимо ОДЗ і маємо, . Вводимо підстановку , Рівняння набуде нового вигляду:

, =.

Нехай .  =, .

Маємо: 1)  

2) ,

3), ,  . ,

Відповідь.

Приклад 2. Розв’язати рівняння

Розв’язання. Область допустимих значень: Виконаємо підстановку і отримаємо рівняння ,. Оскільки на проміжку то

Використаємо формули зведення та перетворення різниці косинусів двох аргументів у добуток, маємо

Останнє рівняння рівносильне сукупності двох рівнянь:

1)

2)

На відрізку маємо корені  . Отже, знаходимо корені рівняння:

.                    

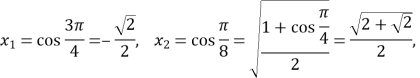
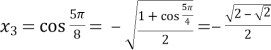  Відповідь. ;

Приклад 3. Розв’язати рівняння  8

Розв’язання. Розділимо ліву та праву частину рівняння на 2. Маємо 4. Оцінимо ліву та праву частину рівняння.

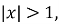1.               Якщо то 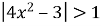, , 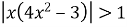але ж 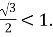За таких умов рівняння коренів не має.
2.               Якщо 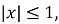тоді скористаємося підстановкою 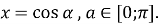Перепишемо рівняння в іншому вигляді 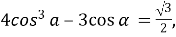ліва частина якого є 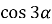, тобто 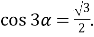Маємо найпростіше тригонометричне рівняння, розв’язком якого є серія коренів 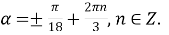Враховуючи обмеження 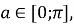повертаємось до підстановки і маємо ==, =.

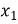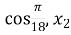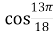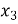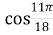Відповідь..

Приклад 4. Розв’язати рівняння .

Розв’язання. Шляхом введення заміни запишемо рівняння так:

Після введення підстановки знову приходимо до рівняння 4 Серед коренів , , які одержали в попередньому рівнянні, лише

Отже,

Відповідь.

Якщо рівняння має вигляд  , то шляхом введення підстановки t, зводимо до рівняння, рівносильного даному:= , розв’язком якого є ті значення для яких :.