Конспект уроку на тему: " Раціональні рівняння "

 

8 клас.

 

Предмет: алгебра

Урок:  Розв’язування типових вправ

 

 

Урок розробив вчитель вищої кваліфікаційної

категорії Мастицька Надія Володимирівна

 

 

 

 

 Навчально – виховний комплекс: загальноосвітня школа І – ІІІ ступенів -    

                                             гімназія №6 ВМР

 

 

 

Тема: Розв’язування раціональних рівнянь 

І. Актуалізація опорних знань.
 

Що ви знаєте про рівняння? 
 

 Рівняння- це рівність, яка містить невідомі числа, позначені буквами.

 Розв’язати рівняння – це означає знайти всі його корені або показати, що їх немає.  Коренем рівняння називають те значення невідомого, при якому рівняння перетворюється на правильну рівність.

 Будь-який доданок можна перенести з однієї частини рівняння в іншу, змінивши його знак на протилежний. При цьому дістанемо рівняння, яке має такі самі корені, що й дане.

 Якщо обидві частини рівняння помножити або поділити на одне й те сааме число, відмінне від нуля, то дістанемо рівняння, яке має такі самі корені, що й дане.

Два рівняння називають рівносильними, якщо вони мають одні й ті самі корені. Рівносильними вважають і такі рівняння, які не мають коренів.

Значення змінних, при яких вираз має зміст, називають допустимими значеннями змінних.

 Рівняння називається раціональним, якщо його ліва і права частини-раціональні вирази.  Раціональне рівняння називається дробовим, якщо його права або ліва частини-дробові вирази.

 

Тест «Перевір себе»

1. Рівність, що містить змінну, називається … 

А) нерівністю;

Б) виразом;

В) тотожністю;

Г) рівнянням.

2. Число, яке задовольняє рівняння, називається його … 

А) значенням;

Б) коренем;

В) змінною;

Г) областю визначення.

3. Розв'язати рівняння означає … 

А) спростити його;

Б) знайти область допустимих значень;

В) знайти всі його корені;

Г) знайти всі його корені, або довести що їх немає.

4. Вирази, що містять дії додавання, віднімання, множення, ділення та піднесення до степеня, називають … 

А) раціональними;

Б) цілими;

В) буквеними;

Г) цілими раціональними виразами.

5. Значення змінних, при яких вираз має зміст, називають ... 

А) множиною значень;

Б) допустимими значеннями змінних;

В) розв'язком рівняння;

Г) розв’язком нерівності.

6. Укажіть допустимі значення змінної у виразі  

А) усі числа, крім -1; 2;

Б) усі числа, крім 5;

В) усі числа, крім 2; -3;

Г) усі числа, крім -1; 5.

7. Рівняння, ліва і права частини яких є раціональними виразами, називають… 

А) дробовими;

Б) раціональними;

В) цілими раціональними;

Г) лінійними.

8. Щоб дріб дорівнював нулю, необхідно, щоб … 

А) знаменник і чисельник дорівнювали нулю;

Б) знаменник дорівнював нулю, а чисельник не дорівнював нулю;

В) чисельник і знаменник не дорівнювали нулю;

Г) чисельник дорівнював нулю, а знаменник не дорівнював нулю.

ІІ. Презентація трьох способів розв'язування дробово – раціональних рівнянь.

 

1. Розв'язати рівняння

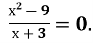
Використання умови рівності дробу нулю: дріб  дорівнює нулю тоді і тільки тоді, коли а = 0 і b ≠ 0.

Алгоритм:

за допомогою тотожних перетворень звести рівняння до виду= 0;

прирівняти чисельник а до нуля і розв’язати утворене ціле рівняння;

виключити з його коренів ті, при яких знаменник дробу b дорівнює нулю.

 

Розв'язання.

 Дріб дорівнюватиме нулю, якщо  чисельник х²-9 буде дорівнювати нулю, а знаменник х+3, при цьому значенні змінної, буде відмінний від нуля.

Отже, х²-9 = 0; х² = 9;  х = 3 або х = -3.

Але, при х =-3 знаменник х+3 = -3+3 = 0. Тому х =-3 не є коренем вихідного рівняння.

При х=3 знаменник х+3 = 3+3 = 6≠0. Отже, х=3 – єдиний корінь даного рівняння.

Відповідь. х=3.

2. Розв'язати рівняння

 

Використання основної властивості пропорції: якщо=(де b≠0, d≠0), то ad = bc.

Алгоритм:

за допомогою тотожних перетворень звести рівняння до виду= ;

використовуючи основну властивість пропорції, дістати ціле рівняння ad = bc, та розв’язати його;

      виключити з його коренів ті, при яких знаменники b або d дорівнюють   нулю.

Розв'язання.

Зведемо рівняння до виду
 

За основною властивістю пропорції маємо:

(х – 2)(х – 8) = (х + 4)(х + 4) при умові, що х + 4 ≠ 0 і  х – 8 ≠ 0.

Розв'яжемо утворене ціле рівняння:

х²-8х-2х+16 = х ²+8х+16;  -10х-8х = 0; -18х = 0;   х = 0.

Перевіримо умови х+4 ≠ 0 та х-8 ≠ 0. Якщо х = 0, то х+4 = 0+4 = 4 ≠ 0; Якщо х = 0, то х-8 = 0-8 = -8 ≠ 0.

Отже х = 0 – корінь даного рівняння.

Відповідь. х = 0.

 

 

3.Розв'язати рівняння

 

Метод множення обох частин рівняння на спільний знаменник дробів.

Алгоритм:

розкласти на множники знаменники дробів, якщо це можливо;

знайти найменший спільний знаменник дробів, що входять у рівняння;

помножити обидві частини рівняння на цей спільний знаменник;

розв’язати утворене ціле рівняння;

виключити з його коренів ті, при яких спільний знаменник дробів перетворюється на нуль.

Розв'язання.

Розкладемо на множники знаменники дробів:

 

Спільним знаменником усіх дробів є (х-1)(х+1). Помножимо обидві частини рівняння на цей вираз, за умови, що (х-1)(х+1)≠0. Маємо:

;

Після скорочення, розв'яжемо утворене ціле рівняння.

2 = х(х-1) – х(х+1);  2 = х²-х-х²-х;  -2х = 2;  х = -1.

Але, якщо х = -1, спільний знаменник (х-1)(х+1) = (-1-1)(-1+1) = 0. Тому число -1 не є коренем даного рівняння.

Відповідь. Рівняння немає коренів.

 

 

 
Проаналізувавши алгоритми, можна зазначити таке:

• розглянуті способи – алгоритми розв’язання дробових рівнянь відрізняються лише способом переходу до цілого рівняння, серед коренів якого можуть бути корені даного дробового рівняння;
• загальні положення розв’язання дробових рівнянь є незмінними: перейшовши до цілого рівняння та розв’язавши це ціле рівняння, слід перевірити, чи не перетворюють корені цілого рівняння знаменники дробів на нуль.

.ІІІ. Самостійна робота (індивідуальний контроль)

Розв’яжіть рівняння: ( де n – порядковий номер учня в списку класного журналу)

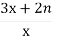1. = 1;
2. ;
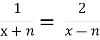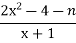3. =  2x+n.

 

Відповідь: 1) – N; 2) – 3N; 3) – 2. 
Відповідь до тесту «Перевір себе»: А; Б; Г; А; Б; В; Б; Г.

ІV. Домашнє завдання.

 

Обери відповідний алгоритм та розв'яжи.

 

1. 
2. 
3. 
4. 
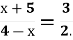
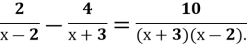
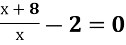
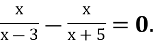
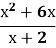5. =0

 

іб 6/(x-6 )дорівнює нулю?

Самоконтроль: 
 
2. Презентаціятрьохспособіврозв'язуваннядробово – раціональнихрівнянь 
Покажи мені – і я запам’ятаю. 
Дай менідіяти самому – і я навчуся. 
Китайськамудрість

Розв'язатирівняння x/(x-4)-16/(x^2-4x)=0 
Використанняумовирівностідробу нулю: дріб a/b дорівнює нулю тоді і тількитоді, коли а=0 і b≠0.

• за допомогоютотожнихперетвореньзвестирівняння до виду a/b=0;
• прирівнятичисельник а до нуля і розв’язатиутворенецілерівняння;
• виключити з йогокоренівті, при якихзнаменникдробу b дорівнює нулю.

Національнийісторико-архітектурнийзаповідник «Кам’янець»

Розв'язатирівняння (3x-5)/(x-1)=(3x-7)/(x-2) 
Використанняосновноївластивостіпропорції: якщо a/b=c/d (де b≠0, d≠0), то ad = bc.

1. за допомогоютотожнихперетвореньзвестирівняння до виду a/b=c/d;
2. використовуючиосновнувластивістьпропорції,дістатицілерівнянняad = bc, та розв’язатийого;
3. виключити з йогокоренівті, при якихзнаменники b або d дорівнюють нулю.

Києво-Печерська Лавра

Розв'язатирівняння (x^2+17)/(x^2-1)= (x-2)/(x+1)+5/(x-1) 
Метод множенняобохчастинрівняння на спільнийзнаменник дробів

1. розкласти на множникизнаменники дробів, якщоцеможливо;
2. знайтинайменшийспільнийзнаменник дробів, щовходять у рівняння;
3. помножитиобидвічастинирівняння на цейспільнийзнаменник;
4. розв’язатиутворенецілерівняння;
5. виключити з йогокоренівті, при якихспільнийзнаменник дробів перетворюється на нуль.

Державнийісторико-архітектурнийзаповідник "Хотинськафортеця"

Вчитель. 
Проаналізувавшиалгоритми, можназазначититаке:

• розглянутіспособи – алгоритмирозв’язаннядробовихрівняньвідрізняютьсялише способом переходу до цілогорівняння, середкоренівякогоможуть бути кореніподаного дробового рівняння;
• загальніположеннярозв’язаннядробовихрівнянь є незмінними: перейшовши до цілогорівняння (яке є наслідкомподаногорівняння) та розв’язавшицецілерівняння, слідврахувати ОДЗ поданого дробового рівнянняабоперевірити, чи не перетворюютькореніцілогорівняннязнаменникрівняння на нуль.

Корекційнавправа (розвитокуваги) 
Розв'язатирівнянняусно: 1) (x-3)/x=0; 2) (x+2)/(x-1)=0; 3) x/(x-8)=0; 4) (x+6)(x-1)/(1-x)=0; 5) (|x|-5)/(x-5)=0. 
Національнийдендрологічний парк «Софіївка»

Запам'ятай!

• перед розв’язуваннямдробово – раціональнихрівняньпотрібновизначити вид рівняння, а вжепотімвибиративідповіднийспосібрівносильнихперетворень;
• вибравшипевний алгоритм перетворень дробового рівняння, слідчіткодотримуватитількицього алгоритму, не перескакувати на інший;
• рівняннявважаютьрозв’язаним, якщовиконано всю послідовністьдій, передбачену алгоритмом.

V. Удосконаленнявмінь і навичок V.1. Розв'язуванняраціональнихрівнянь

Найкращийспосібвивчитищо – небудь – цевідкрити самому.  Д. Пойа

Колективне і коментованерозв'язуваннявправіззапропонованогоперелікурівнянь, ученьмає право вибору, але завдання подано по рівняхскладності і оцінюєтьсявідповідноюкількістюбалів 
 

СофіяКиївська

Херсонес Таврійський

V.1. Розв'язуваннязадач за допомогоюрівнянь 

Розв'язування задач є найхарактернішим і специфічнимрізновидомвільногомислення. В. Джеймс

1) Катер проходить 160 км за течієюрічки за той час, що й 140 км протитечії. Знайтивласнушвидкістькатера, якщошвидкістьтечіїрічкидорівнює 2км/год. 
2)Додатково. Знаменникдробу на 4 більшийвідйогочисельника. Якщо до чисельникадробудодати 11, а відзнаменникавідняти 1, то вийдедріб, оберненийданому. Знайтицейдріб.

Національнийзаповідник-острів «Хортиця»

VІ. Застосуваннязнань, уміньі навичок.

Самостійна робота (індивідуальнийконтроль) 

Через рівняння, теореми я будь – якірозв’язувавпроблеми. Джеффі Чосер

Розв’яжітьрівняння: ( де N – порядковий номер учня в списку класного журналу)

1. (3x+2N)/x=1;
2. 1/(x+N)=2/(x-N);
3. (2x^2-4-N)/(x+1)=2x+N.

Відповідь: 1) – N; 2) – 3N; 3) – 2. 
VІ. Підсумок уроку.

Більшістьжиттєвих задач розв’язуються як алгебраїчнірівняння, звезеннямїх до найпростішого виду. (Л. Толстой)

Оцінюванняучнів 
Учнямпропонуєтьсявисловитисящодопідсумкууроку 
VІІ. Домашнєзавдання.

Чеснозробленамаленька робота – шлях довеликої перемоги

Повт. §8, запитання 1-3 ст.47