Конспект уроку на тему "Розв’язування задач і вправ. Ірраціональні числа. Дійсні числа."

          Богдан Юлія

Урок №35        Дата ___________

Тема: Розв’язування задач і вправ. Ірраціональні числа. Дійсні числа.

Мета:

Навчальна: закріпити поняття про числові множини, сформувати поняття про ірраціональне число, дійсне число;

Розвивальна: розвинути в учнів уявлення про розширення поняття числа, ерудицію, інтелект учнів;

Виховна: виховувати вміння концентрувати свою увагу, дисципліну, звичку до систематичної розумової праці.

Обладнання: Підручник з математики 8 клас (Мерзляк), Збірник задач і контрольних робіт з алгебри 8 клас (Мерзляк).

Хід уроку

1. Організаційний етап

• Привітання
• Перевірка присутності учнів на уроці
• Перевірка готовності учнів та кабінету до уроку

2. Перевірка домашнього завдання

Чи є в когось запитання до домашнього завдання? Якщо є запитання, то відповідаю на них, якщо ж ні, то учні відкривають зошити, записують число, класна робота, тему уроку: «Розв’язування задач і вправ. Ірраціональні числа. Дійсні числа». А в цей час я перевіряю наявність домашнього завдання проходячи між рядами.

3. Актуалізація опорних знань

1. Які числа називаються натуральними?
2. Які числа називаються цілими?
3. Наведіть приклад дробового числа?
4. Запишіть числа ; ; 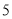у вигляді десяткового дробу. (; 5=5,00;
   )
5. Як називається десятковий дріб, який має вигляд 0,333…? (десятковий нескінченний періодичний дріб)
6. Як називаються числа, які можна подати у вигляді нескінченного десяткового дробу? (раціональні)

Виникає питання чи існують числа відмінні від раціональних? Відповідь на це питання і дамо сьогодні на уроці.

4. Засвоєння нових знань

З історії виникнення чисел

Поняття числа з’явилося в стародавні часи. Воно є одним з найзагальніших понять математики. Необхідність виконувати вимірювання та підрахунки зумовила появу додатних раціональних чисел. Саме тоді виникли і використовувалися натуральні числа і дробові числа, які розглядали як відношення натуральних чисел.

Наступним етапом розвитку поняття числа є введення у практику від’ємних чисел. У Стародавньому Китаї ці числа з’явилися у ІІ ст. до н.е. Там уміли додавати і віднімати від’ємні числа. Від’ємні числа тлумачили як борг, а додатні як майно. В Індії в VII ст. ці числа розуміли так само, але вже знали і правила множення та ділення.

Цілі числа (додатні, від’ємні та 0 ), дробові числа (додатні та від’ємні) складають множину раціональних чисел. Раціональними їх називають тому, що кожне з них можна записати у вигляді частки двох чисел, а слово «частка» латинською мовою – ratio.

Усі натуральні числа утворюють множину натуральних чисел, яку позначають буквою ; а всі цілі числа – множину цілих чисел, яку позначають буквою .

Термін «множина» використовують, коли йдеться про набір, сукупність будь-яких об’єктів, об’єднаних за певною ознакою. Наприклад, множина учнів школи, множина дерев у парку, множина букв алфавіту тощо. Поняття «множина» належить до основних понять математики, таких як «число», «точка», «пряма», тому його не означують.

Об’єкти, які утворюють множину, називають елементами множини. Так, число 5 – елемент множини натуральних чисел. Для позначення множин використовують великі букви латинського алфавіту (A, B, …), а для позначення елементів множини – малі букви (a, b, …).

Якщо а є елементом множини М, то записують: . Читають а належить М.

Якщо b не є елементом множини М, то записують: . Читають b не належить М.

Ми вже знаємо, що будь-якого раціональне число можна записати у вигляді , де  m - ціле число, n  - натуральне число. Наприклад, . Кожне раціональне число можна подати також у вигляді нескінченного десяткового періодичного дробу. Для цього треба чисельник дробу поділити на його знаменник, наприклад . І кожний нескінченний десятковий періодичний дріб є записом деякого раціонального числа, наприклад .

Але в математиці існують числа, які не можна записати у вигляді , де  m - ціле число, n  - натуральне число.

Числа, які не можна записати у вигляді , де  m - ціле число, n  - натуральне число, називаються ірраціональними числами.

Префікс ір означає заперечення, ірраціональні означає не раціональні. Прикладами ірраціональних чисел є тощо. Множина ірраціональних чисел позначається буквою I.

Кожне ірраціональне число можна подати у вигляді нескінченного десяткового неперіодичного дробу. Наближене значення ірраціонального числа можна знаходити з певною точністю за допомогою мікрокалькулятора або комп’ютера, наприклад

Раціональні числа разом з ірраціональними числами утворюють множину дійсних чисел.

З історії дійсних чисел

Дійсні числа входили в математику досить довго. Вчені античного світу не допускали і думки, що крім цілих і дробових можуть існувати ще якісь інші числа. Хоч Піфагор (VI ст. до н.е.) та його учні довели, що коли довжина квадрата дорівнює одиниці, то довжину його діагоналей не можна виразити ніяким раціональним числом. Тим самим вони встановили існування відрізків, довжини яких не виражаються раціональними числами. Та все ж таки ірраціональних чисел не ввели. Математики Індії та Середнього Сходу користувалися ірраціональними числами, але вважали їх не справжніми, неправильними, глухими. Тільки коли Рене Декарт запропонував кожній точці координатної прямої ставити у відповідність число, ірраціональні числа довелося об’єднати з раціональними числами в одну множину дійсних чисел. Строга теорія дійсних чисел опрацьована тільки в XIX ст.

Множину дійсних чисел позначать буквою .

Оскільки кожне натуральне число є цілим числом, то множина натуральних чисел є частиною множини цілих чисел, тобто її підмножиною. Аналогічно множина є підмножиною множини , а множина є підмножиною множини .

Дійсні числа, що записані за допомогою нескінченних десяткових неперіодичних дробів можна порівнювати за тими самими правилами, що й нескінченні десяткові дроби. Наприклад, ;
.

При додаванні, відніманні, множенні і діленні (на відмінне від нуля число), піднесенні до степеня дійсних чисел мають місце всі властивості, що й для дій над раціональними числами. Розв’язуючи прикладні задачі, дійсні числа, а саме ірраціональні числа, замінюють наближеними значеннями, округлюючи до певного розряду.

Наприклад, обчислити з точністю до тисячних

5. Вправи для закріплення

№ 444 (Алгебра 8 клас Мерзляк)

Методичний коментар: для того щоб дати відповіді на запитання даної задачі слід використати знання про натуральні, цілі, дробові, раціональні та ірраціональні числа.

№ 447 (Алгебра 8 клас Мерзляк)

Які з даних нескінченних дробів є записами раціональних чисел, а які – ірраціональних.

1. 0,(3);
2. 0,4(32);
3. 0,2020020002000020…

Методичний коментар: для того щоб розв’язати дане завдання слід досконало володіти поняттями раціональне та ірраціональне число. У пунктах 1 та 2 записані нескінченні періодичні десяткові дроби які є раціональними числами, а в пункті 3 записано нескінченний неперіодичний дріб.

№ 450 (Алгебра 8 клас Мерзляк)

Розв’язання:

1. 1,73
2. 1,74

Методичний коментар: для того щоб записати наближене значення з надлишком записуємо лише 2 знаки після коми, для того щоб записати наближене значення з надлишком 2 знак після коми збільшують на 1.

№ 452 (Алгебра 8 клас Мерзляк)

Розв’язання:

1. а=4;
2. а=3
3. а=-9

Методичний коментар: для того щоб розв’язати дане завдання слід пригадати що таке степінь числа з натуральним показником, та як розв’язують рівняння такого типу, а також поняття раціонального та ірраціонального чисел.

№ 453 (Алгебра 8 клас Мерзляк)

Методичний коментар: для того щоб розв’язати дане завдання слід пригадати правила порівняння десяткових дробів, правила перетворення звичайних дробів у десяткові та значення числа .

6. Підбиття підсумків уроку

• Що нового ви дізналися сьогодні на уроці?
• Що було для вас уже відомим?
• Що було цікавим на уроці?
• Над чим ще варто попрацювати?

7. Домашнє завдання

§ 14 № 445, 451, 456.