Конспект уроку на тему "Симетрія відносно точки і прямої"

          Богдан Юлія

Урок № 48        Дата ___________

Тема: Симетрія відносно точки і прямої.

Мета:

Навчальна: формування поняття симетрії відносно точки/прямої; вивчення властивостей симетрії відносно точки/прямої; формування вмінь застосовувати вивчені означення і властивості до розв'язування задач;

Розвивальна: сприяти розвитку просторової уяви, пам’яті, уваги;

виховувати почуття відповідальності, інтерес до предмета, уміння організовувати свою роботу та розраховувати час.

Обладнання: Підручник з математики 9 клас (Мерзляк), Збірник задач і контрольних робіт з алгебри 9 клас (Мерзляк).

Хід уроку

1. Організаційний етап

• Привітання
• Перевірка присутності учнів на уроці
• Перевірка готовності учнів та кабінету до уроку

2. Перевірка домашнього завдання

Чи були у вас проблеми при виконанні завдань? Якщо так, то один з учнів хто виконав це завдання пояснює його біля дошки. Якщо ні, то просто перевіряю наявність домашньої роботи у зошитах.

3. Актуалізація опорних знань

1. Яке перетворення фігури називається переміщенням?
2. Доведіть, що під час руху точки, які лежать на прямій, переходять у точки, які також лежать на прямій, і зберігається порядок їх взаємного розміщення.
3. У що переходять прямі, відрізки при переміщенні?
4. Доведіть, що при переміщенні зберігаються кути.
5. Периметри двох ромбів рівні. Чи випливає з цього, що і ромби рівні?
6. Периметри двох квадратів рівні. Чи рівні квадрати?

4. Засвоєння нових знань

Перетворення фігур за допомогою переміщення має декілька видів. Сьогодні ми ознайомимося з перетворенням фігури за допомогою симетрії відносно точки та прямої. Розглянемо, спочатку симетрію відносно точки.

Означення. Точки A і A₁ називають симетричними відносно точки O, якщо точка O є серединою відрізка AA₁ (рис. 19.1). Точку O вважають симетричною самій собі.

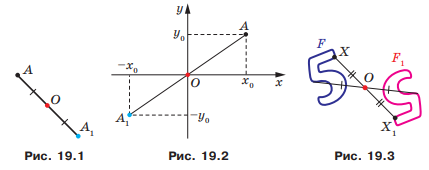
Наприклад, точки A і A₁, у яких як абсциси, так і ординати — протилежні числа, симетричні відносно початку координат (рис. 19.2).

Розглянемо фігуру F і точку O. Кожній точці X фігури F поставимо у відповідність симетричну їй відносно точки O точку X₁. Унаслідок такого перетворення фігури F отримаємо фігуру F₁ (рис. 19.3). Таке перетворення фігури F називають центральною симетрією відносно точки O. Точку O називають центром симетрії. Також говорять, що фігури F і F₁ симетричні відносно точки O.

Означення. Фігуру називають симетричною відносно точки O, якщо для кожної точки даної фігури точка, симетрична їй відносно точки O, також належить цій фігурі.

Для побудови точки А’ симетричної точці А відносно точки О слід:

1. Провести промінь АО
2. По інший бік від точки О відкласти відрізок ОА’ рівний відрізку ОА. (рис. 19.1)

Властивості симетрії відносно точки (центральної симетрії)

1.     Перетворення симетрії відносно точки є переміщенням.
2.     Перетворення симетрії відносно точки перетворює пряму на паралельну їй пряму або на себе; відрізок — на рівний і паралельний йому відрізок; многокутник — на рівний йому многокутник.
3.     Будь-яка пряма, що проходить через центр симетрії, відображається при цій симетрії на себе. Якщо перетворення симетрії відносно точки О переводить фігуру F у себе, то вона називається центральносиметричною, а точка О — центром симетрії.
4.     При симетричному відображені точок у декартовій системі координат відносно початку координат кожна координата точки змінює свій знак на протилежний. Початок координат є симетричний сам до себе.

Означення. Точки A і A₁ називають симетричними відносно прямої l, якщо пряма l є серединним перпендикуляром відрізка AA₁ (рис. 18.1). Якщо точка A належить прямій l, то її вважають симетричною самій собі відносно прямої l.

Наприклад, точки A і A₁, у яких ординати рівні, а абсциси - протилежні числа, симетричні відносно осі ординат (рис. 18.2).

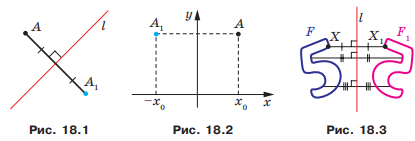
Розглянемо фігуру F і пряму l. Кожній точці X фігури F поставимо у відповідність симетричну їй відносно прямої l точку X₁. Унаслідок такого перетворення фігури F отримаємо фігуру F₁ (рис. 18.3). Таке перетворення фігури F називають осьовою симетрією відносно прямої l. Пряму l називають віссю симетрії. Говорять, що фігури F і F₁ симетричні відносно прямої l.

Означення. Фігуру називають симетричною відносно прямої l, якщо для кожної точки даної фігури точка, симетрична їй відносно прямої l, також належить цій фігурі.

Пряму l називають віссю симетрії фігури. Також говорять, що фігура має вісь симетрії.

Властивості осьової симетрії

1.     Перетворення осьової симетрії є переміщенням.
2.     Осьова симетрія перетворює пряму на пряму; відрізок — на відрізок; многокутник — на рівний йому многокутник.
3.     Точки, що належать осі симетрії, відображаються самі на себе.

5. Вправи для закріплення

Індивідуальна робота біля дошки. Учні по черзі виходять до дошки та виконують з детальним коментуванням запропоновані завдання. (К. – володіння державною та рідною мовою)

№ 909 (Мерзляк)

А’(2;3), В’(-4;-5)

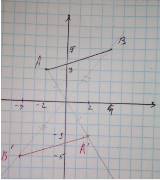
Методичний коментар: для того щоб знайти точки симетричні даним відносно початку координат слід використати властивість 4 симетрії відносно точки.

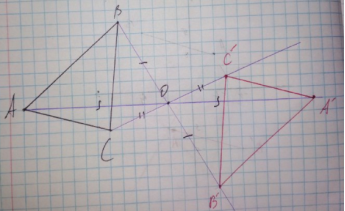
№ 19.1 (Мерзляк)

Методичний коментар: для того щоб побудувати трикутник симетричний даному необхідно скористатися алгоритмом побудови точки симетричної відносно деякої точки. Таким чином отримаємо образи вершин даного трикутника сполучивши які отримаємо трикутник симетричний даному відносно точки О.

№ 110 (Мерзляк збірник)

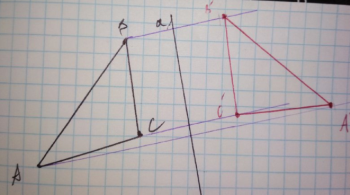
Накресліть довільний трикутник АВС та пряму а, що лежить поза цим трикутником та побудуйте трикутник симетричний даному відносно прямої а.

Методичний коментар: для того щоб побудувати трикутник симетричний даному відносно прямої а необхідно користуючись алгоритмом побудови точки симетричної відносно прямої знайти образи всіх вершин даного трикутника та сполучити їх..

№ 178 (Мерзляк)

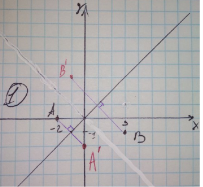
1. Бісектриса I i III координатних кутів – це пряма y=x. А(-2;0) => А'(0;-2)  В(3;-1) => B'(-1;3)
2. Бісектриса II i IV координатних кутів – це пряма y=-x. А(-2;0) => А'(0;2)  В(3;-1) => B'(1;-3)

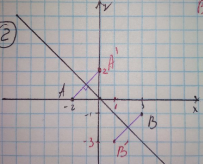
Методичний коментар: для того щоб знайти відображення точок слід побудувати у системі координат точки та прямі і користуючися правилами побудувати симетричні точки.

6. Підбиття підсумків уроку

• Які точки називаються симетричними відносно прямої/точки?
• Яке перетворення називається симетрією відносно даної прямої/точки?
• Яка фігура називається симетричною відносно даної прямої/точки?

7. Домашнє завдання

§ 18,19 № 18.2, 18.25, 19.2.