Урок 2

Тема уроку.   Тригранний і многогранний кути.

Мета уроку:   формування понять тригранний і многогранний кут; грані, ребра, вершина і двогранні кут тригранного кута, формування умінь учнів знаходити окремі елементи тригранних кутів.

Обладнання: моделі многогранників, схема “Співвідношення між елементами прямокутного трикутника” (с. 19).

І. Перевірка домашнього завдання

1. Один учень відтворює на дошці розв'язування домашньої задачі № 1 (2).

2. Фронтальне опитування.

1) Сформулюйте означення двогранного кута.

2) Що таке грань, ребро двогранного кута?

3) Сформулюйте означення лінійного кута двогранного кута.

4) Чи залежить міра двогранного кута від вибору лінійного кута? Чому?

5) Яким чином можна побудувати лінійний кут двогранного кута?

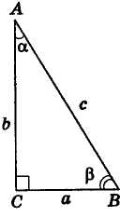
6) Лінійний кут – АВС (рис. 14) двогранного кута з ребром MN дорівнює 45°, Укажіть, які з наведених тверджень правильні, а які – неправильні:

а) площина АВС перпендикулярна до прямої MN;

б) <MBA > 90°;

в) <ABN = 45°;

г) площина АВС перпендикулярна до площини ABN;

д) якщо АВ = ВС, то <BCA = 90°.

3. Обговорення розв'язування задачі № 1 (2).

II. Сприйняття та усвідомлення нового матеріалу. Тригранний кут.

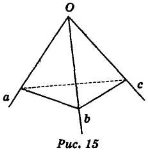
Побудуємо три промені a, b, с, які виходять з однієї точка O і не лежать в одній площині (рис. 15).

Тригранним кутом (аbс) називається фігура, яка складається з трьох плоских кутів (ab), (bс), (ас),

Ці плоскі кути називаються гранями тригранного кута, а їх сторони а, b, с – ребрами тригранного кута. Спільна вершина плоских кутів (точка О) називається вершиною тригранного кута. Двогранні кути, утво­рені гранями тригранного кута, називаються двогранними кутами три­гранного кута.

Розв'язування задач

1. Знайдіть в оточенні тригранні кути та вкажіть їх грані, ребра та двогранні кути.
2. Знайдіть на моделях многогранника (куба, тетраедра, прямокутно­го паралелепіпеда) тригранні кути та вкажіть їх грані, ребра та двогранні кути.
3. У тригранного кута два плоскі кути по 45°, двогранний кут між ними прямий. Знайдіть третій плоский кут. (Відповідь. 60°.)
4. Доведіть, що в кожному тригранному куті проти рівних плоских кутів лежать рівні двогранні кути.
5. Доведіть, що коли всі двогранні кути тригранного кута рівні, то рівні і всі його плоскі кути.
6. Усі плоскі кути тригранного кута дорівнюють по 60°. Знайдіть його двогранні кути. (Відповідь, агссоs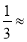70°82'.)
7. Якщо два плоскі кути тригранного кута гострі й рівні між собою, то проекція їх спільного ребра на площину третього кута с бісект­рисою цього кута. Доведіть.
8. У тригранного кута два плоскі кути по 60°, а третій — 90°. Знай­діть кут між площиною прямого кута і протилежним ребром. (Від­повідь. 45°.)

9*. Якщо в тригранному куті один плоский кут прямий, прилеглі до нього двогранні кути дорівнюють по 15°, то третій двогранний кут дорівнює 130°. Доведіть.

10. У тригранного кута SASC плоскі кути ASB, ASC і двогранний кут при ребрі SA мають величину 60°. Знайдіть величину кута BSC.

   (Відповідь, агссоs.)

11. У тригранному куті два плоскі кути дорівнюють по 45°, а двогран­ний кут між ними — 60° · Знайдіть третій плоский кут. (Відповідь.  arccos.)

12. Задача № 2 із підручника (с. 76).

13. Задача № 4 із підручника (с. 77).

п-гранний кут                                  

Розглянемо n променів a₁, a₂,... a_n, які ви­ходять з однієї точки О, і жоден із трьох про­менів не лежить в одній площині.

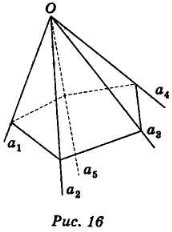п-гранним куmoм (а₁а₂а₃...а_n) називається фігура, яка складається з n плоских кутів (а₁а₂), (а₂а₃), ...,     (а_n-1a_n), (a_na₁) (рис. 16).

Ці кути називаються гранями, п-гранного кута, а їх сторони — ребрами. Спільна вер­шина плоских кутів називається вершиною n-гранного кута. Двогранні кути, утворені су­сідніми гранями                n-гранного. кута, називають­ся двогранними кутами п-гранного кута.

III. Домашнє завдання

§ 6, π. 38; контрольні запитання № 4—5; задача № 3 (с. 76).

IV. Підведення підсумку уроку

Запитання до класу

1) Дайте означення тригранного кута та його елементів (грані, ребра, вершини, двогранні кути).

2) Дайте означення п-гранного кута та його елементів (грані, ребра, вершини, двогранні кути).

3) У кубі АВСDА₁В₁С₁D₁, розглядається тригранний кут β вершиною А і плоскими кутами, ВАС, A₁АB, A₁AC Знайдіть:

а) величину плоского кута Α₁ΑΒ;     

б) величину двогранного кута з ребром АА₁.

При розв'язуванні задач на цьому уроці широко застосовуються спів­відношення в прямокутному трикутнику. Якщо учні не мають міцних навичок в знаходженні елементів прямокутних трикутників, то слід ско­ристатися наступною схемою, її можна використовувати і на наступних уроках.