Конспект уроку:"Похідна функції, її фізичний та геометричний зміст"

Конспект уроку(виконати стисло у робочому зошиті ,дата 30 березня)

 

Тема : Похідна функції, її фізичний та геометричний зміст

 

План

1. Поняття похідної функції.
2. Задачі, що приводять до поняття фізичного змісту, похідної  функції.
3. Задачі, що приводять до поняття геометричного змісту похідної.
4. Математична модель знаходження похідної функції.

 

Завдання заняття

Навчитися складати математичну модель знаходження похідної функції

 

Часто буває так, що, розв`язуючи задачі, дуже далекі одна від одної за змістом, ми приходимо  до однієї і тієї самої математичної моделі.

 Особливість математики як науки полягає в тому, що вона розробляє способи оперування з тією чи іншою математичною моделлю, яку потім використовують спеціалісти з інших галузей знань.

Сьогодні йтиметься про принципово нову  для вас математичну модель. Отже, розгляньмо дві різні задачі : фізичного і геометричного змісту, в процесі розв`язування яких саме і виникає нова математична модель.

 

Нехай деяке тіло (матеріальна точка) рухається  по прямій, на якій задані початок відліку, одиниця виміру(метр) і напрям.

Закон руху задано формулою S=s(t), де t – час (у секундах), s(t) – положення тіла на прямій (координата даної матеріальної точки, що рухається у момент часу  t по відношенню до початку відліку (у метрах).

Знайти швидкість руху тіла в момент часу t.

Розв`язання

Нехай тіло в момент часу t було в точці А і пройшло шлях ОА= s(t).

                      

 

         О А В    S

Надамо аргументу t  приріст Δt і  розглянемо ситуацію   в момент часу t+Δt. Координата матеріальної точки змінилась, бо тіло пройшовши шлях від початку руху ОВ= s(t+Δt), перебуватиме в точці В.

Отже, до Δt секунд тіло перемістилося з точки А в точку В,

тобто пройшло шлях АВ.

АВ=ОВ-ОА= s(t+Δt)-s(t).

Візьмемо відрізок АВ= ΔS (м)

Шлях ΔS(м) тіло пройшло за Δt секунд.

Нескладно знайти середню швидкість руху Vс

за проміжок часу [t; t+ Δt]; Vс=

Що означає V(t) в момент часу t (інколи її називають миттєвою швидкістю)?

Можна сказати так :

Це середня швидкість руху за проміжок часу [t; t+Δt] за умовами, що Δt витрачається все менше і менше;

інакше за умови, що Δt  О.

це означає, що V(t)=

ΔS називається приростом шляху.

Приклад

Точка рухається прямолінійно за законом s(t)=4t²- t-2

S – шлях у метрах, t – час у секундах.

Знайдіть швидкість точки :

а) у довільний момент часу t₀;

б) у момент часу t=3 с.

Розв`язання

а)  нехай зафіксовано момент часу t₀, який дістав приріст Δt, тоді t₁= t₀+Δt

Знайдемо відповідний приріст шляху :

ΔS=S(t₀+Δt)–S(t₀) =4(t₀+Δt)² -(t₀+Δt) -2-(4t₀²- t₀-2)=4(t₀²+2 t₀Δt+()²-t₀-Δt-2-4t²+t+2=4t₀²+8t₀Δt+4(Δt)²-t₀-Δt-2-4t₀²+ +t₀+2=8t₀ Δt +4(Δt)²- Δt = Δt ∙(8t₀+4 Δt-1).

Знайдемо відношення

= t₀+4Δt -1,

= =8t₀-1

Значить, V_м= 8t₀-1() у довільний момент часу С. Отже, при заданому русі S(t) миттєва швидкість V(t) у довільний момент часу t обчислюється за формулою

V(t)= 8t-1.

б) якщо t=3 с, то маємо V(3)=8∙3-1=23()

Відповідь: а) 8t₀-1;   б) 23 ()

Терміном дотична ми вже користувалися (на інтуїтивному рівні) в курсі алгебри 8 класу, коли говорили, що парабола у=х² дотикається до осі ОХ у точці х=0 або що одне й те саме, вісь ОХ є дотичною до параболи в точці х=0

 

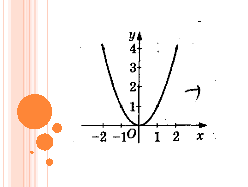
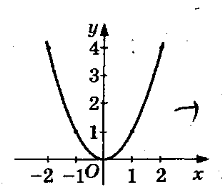
Справа не в тому, що вісь ОХ і парабола мають тільки одну спільну точку. Адже вісь Оу теж має з параболою у=х²  тільки одну спільну точку, але не є дотичною до параболи.

Зазвичай дотичну визначають таким чином :

На даній кривій L вибираємо точку К, а потім ще одну – точку М. Проведемо січну МК – пряму m. Далі будуємо наближену точку М по кривій до точки К, а потім ще одну точку М. проведемо січну МК – пряму m. Далі будемо  наближати точку М по кривій до точки К.

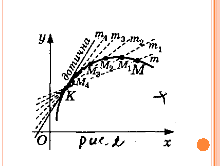
Січна МК буде змінювати своє положення:

Пряма m (її нове положення є m₁, m₂, m₃, m₄…) ніби обертається навколо точки К.

Часто буває так, що в цьому процесі можна виявити пряму, яка являє собою деяке граничне положення січної, цю пряму називають дотичною до кривої α у точці К.

 

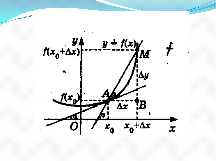
Задача (про дотичну до графіка функції). Дано графік функції у=f(х). на ньому вибрана точка А(х₀; f(х₀)), через яку до графіка проведено дотичну (вважаємо, що дотична існує). Знайти кутовий коефіцієнт дотичної.

Розв`язання. Як відомо дотична – це пряма у=кх+в, яка проходить  через точку А(х₀; f(у₀)); положення прямої  визначається кутовим коефіцієнтом к=tgα, де α – кут між прямою і дотичним напрямом осі ОХ. Надамо аргументу _Хо приросту і розглянемо точку М з абсциссою х₀+Δх

Ордината точки М дорівнює f(_Хо+Δх).Кутовий коефіцієнт прямої (січної АМ) тобто кута між АМ і віссю ОХ, обчислюється за формулою К_січ=, причому ∆у= f(х₀+)- f(х₀). Із ∆АВМ  маємо =tgМАВ=tgα . Якщо о, то точка М почне наближатися по кривій до точки А. Отже, К_доm= _січ 

К_доm=

Зауваження :У задачі не розглядається випадок коли до тична перпендикулярна до осі абсцис.

Рівняння такої прямої х=а, про кутовий коефіцієнт у цьому випадку говорити  некоректно, оскільки він не існує.

 

 

Дві різні задачі привели в процесі розв`язання до однієї і тієї самої математичної моделі – границі відношення приросту функції до приросту аргумент за умови, що приріст аргументу прямує до нуля.

Настав час вивчити нову математичну модель, за допомогою якої розв`язується багато задач.

Нехай функція у=f(х) визначена в точці х та в деякому колі. Надамо аргументи х приріст ∆х, такий, щоб не вийти із   зазначеного околу. Знайдемо відповідний приріст функції ∆у і розглянемо відношення (слайд 10 і 11)

Якщо існує границя відношення при ∆х→0, то вказану границю називають похідною функції у= f(х) у точці Х і позначають f`(х). отже, f`(х) або у´=

f`(х₀)=

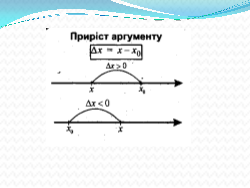
f(х)- f(х₀) – приріст аргумента

        

 

Алгоритм знаходження похідної функції у= f(х)

1. Зафіксувати значення х₀, знайти f(х₀)
2. Надати аргументу х₀ приріст ∆х, перейти в нову точку х₀+∆х, знайти f(х₀+∆х)
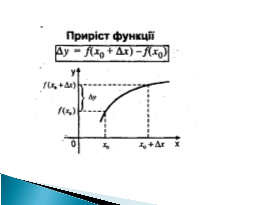
3. Знайти приріст функції: ∆у= f(х₀+∆х)- f(х₀)
4. Скласти відношення
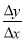
5. Обчислити границю

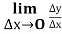
Ця границя і є похідною функції у=f(х) у точці х₀ і позначається f´(х₀) або у´. (слайд 12).

 

 

Позначення похідної у´ і f´(х) ввів французький математик Жозеф Луї Лагранж (1736-1813).

Леонард Ейлер перший почав використовувати позначення ∆(дельта) грецька буква для позначення приросту аргументу ∆х=х₁-х₀ або х₀  і х₁ = х₀+ ∆х. Різниця х₁- х₀= ∆х називається приростом аргументу.

Приріст функції ∆у=у₁-у₀ або різниця f(х₁)-f(х₀)= f(х₀+∆х)- f(х).

Відкриттю похідної і основ диференціального числення передували роботи математика і юриста П`єра Ферма (1601-1665), який у 1929 р. запропонував проведення дотичних до довільних кривих, що фактично спиралися на застосування похідних.

Ісаак Ньютон прийшов до поняття похідної, розв`язуючи задачі про миттєву швидкість.

Готфрід Лейбніц дійшов до похідної функції розглядаючи  геометричну задачу про проведення дотичної до кривої (слайд 13-15)

 

Постановка домашнього завдання(на тиждень З0.03-03.04)

Г. П. Бевз, В.Г. Бевз «Математика» 10 клас   Рівень стандарту &14,15

 

Границя функції в точці — фундаментальне поняття математичного аналізу, зокрема аналізу функцій дійсної змінної, число, до якого прямує значення функції, якщо її аргумент прямує до заданої точки.

 Limited(англ.)   -    ограниченное или предел (рос) границя(укр.)