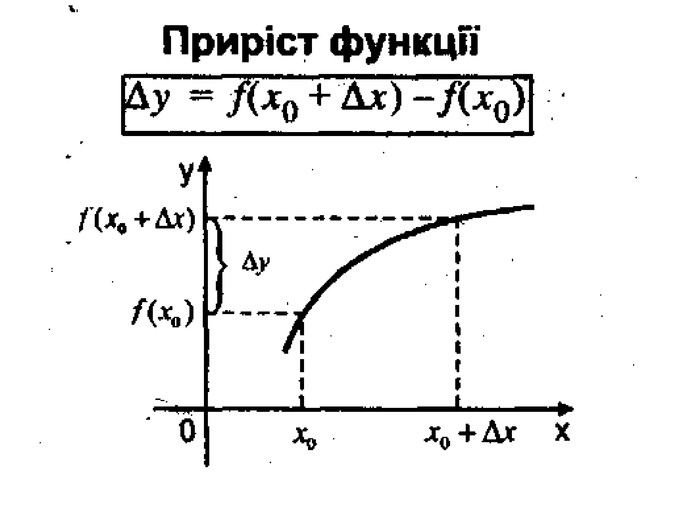
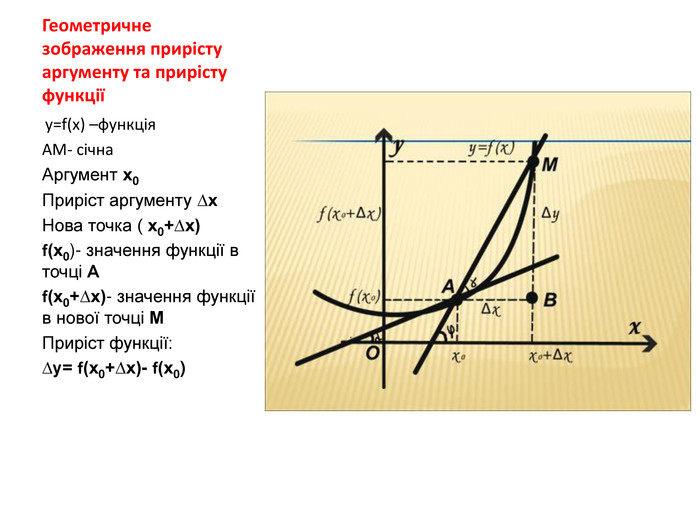
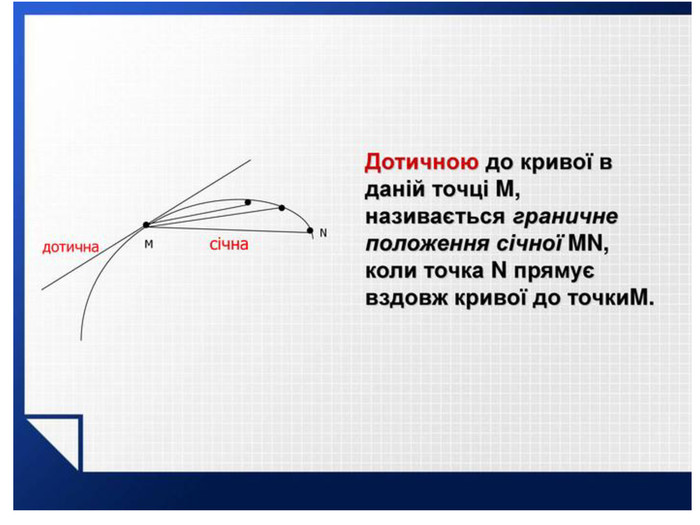
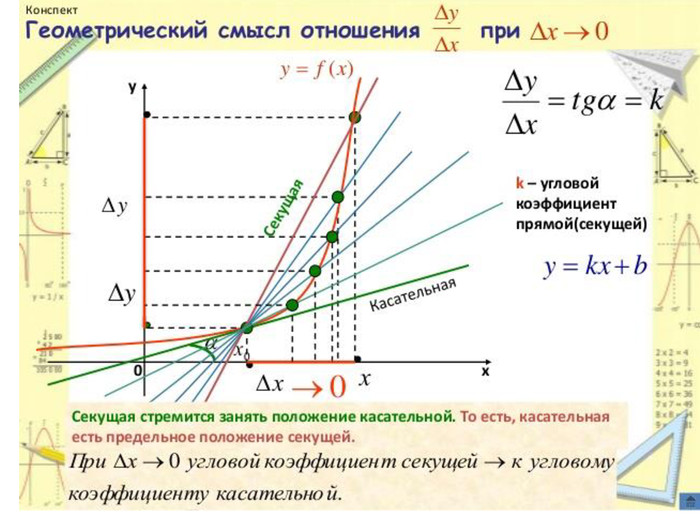
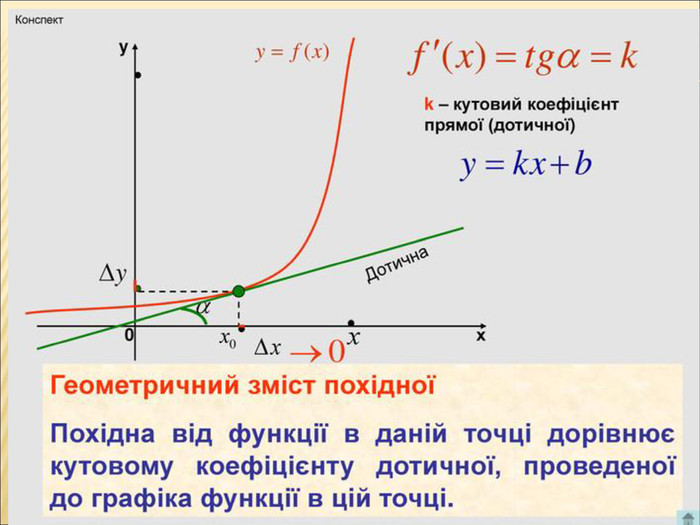
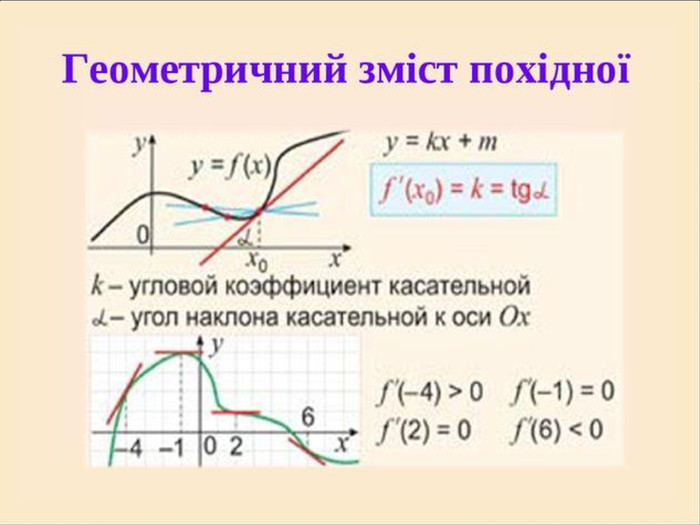
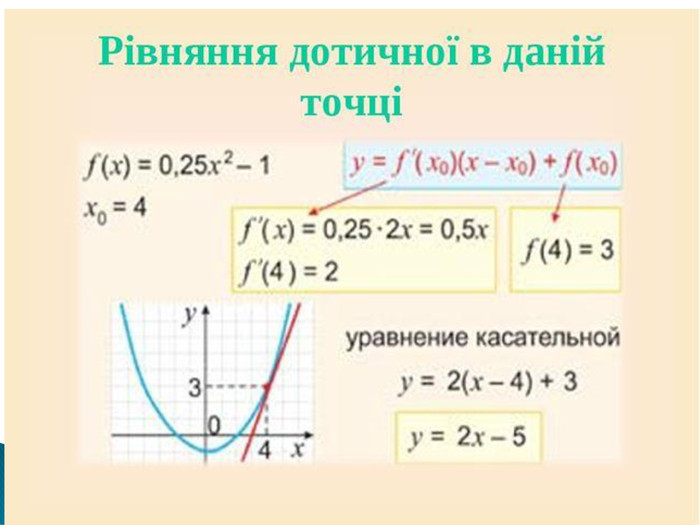
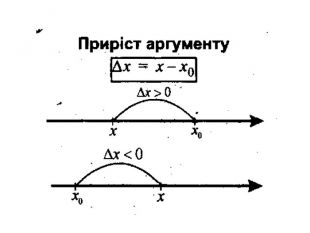
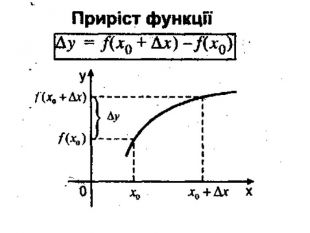
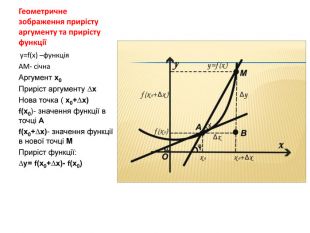
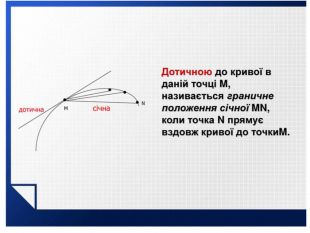
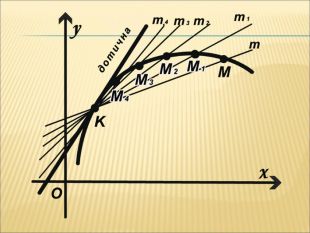
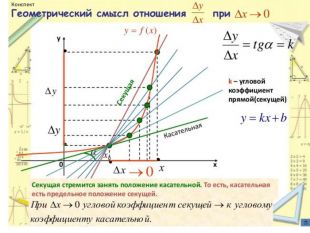
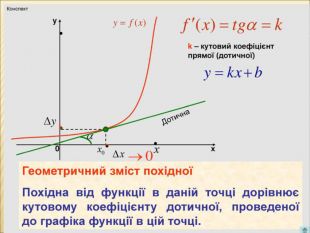
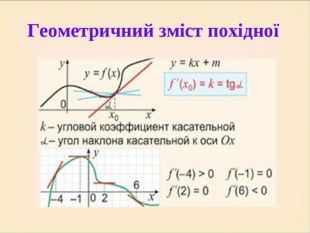
Презентація з теми:"Похідна функції, її фізичний та геометричний зміст".
Про матеріал
Презентация допоможе учням самостійно(під час карантину) засвоіти тему:"Похідна функції, її фізичний та геометричний зміст", навчитися складати математичну модель знаходження похідної функції
Тема: Похідна функції, її фізичний та геометричний зміст
ПЛАНПоняття похідної функції. Задачі, що приводять до поняття фізичного змісту похідної функції. Задачі, що приводять до поняття геометричного змісту похідної функції. Математична модель знаходження похідної функції.
Завдання заняття Навчитися складати математичну модель знаходження похідної функції
Леонард Ейлер(1707-1783)Ввів позначення ∆ (дельта) для позначення приросту: агрументу ∆х=х1-х0 ; функції ∆у=у1-у0 ; f(х1)-f(х0)= f(х0+∆х)- f(х)
Жозеф Луї Лагранж -- французький математик. Ввів позначення похідної у´ або f´(х)
П`єр Фермаматематик та юрист (1601-1665)Дійшли до похідної функції розглядаючи геометричну задачу про проведення дотичної до кривоїГотфрід Лейбніц (1646-1716)
Точка рухається прямолінійно за законом s(t)=4t2- t-2 S – шлях у метрах, t – час у секундах. Знайдіть швидкість точки :а) у довільний момент часу t0;б) у момент часу t=3с.
Геометричне зображення прирісту аргументу та прирісту функції y=f(x) –функція. АМ- січна Аргумент х0 Приріст аргументу ∆х. Нова точка ( х0+∆х)f(х0)- значення функції в точці Аf(х0+∆х)- значення функції в нової точці МПриріст функції: ∆у= f(х0+∆х)- f(х0)
Границя функції в точці — фундаментальне поняття математичного аналізу, зокрема аналізу функцій дійсної змінної, число, до якого прямує значення функції, якщо її аргумент прямує до заданої точки. Limited(англ.) - ограниченное(рос)
Зафіксувати значення х0, знайти f(х0)Надати аргументу х0 приріст ∆х, перейти в нову точку х0+∆х, знайти f(х0+∆х)Знайти приріст функції: ∆у= f(х0+∆х)- f(х0)Скласти відношення ∆у ∆х. Обчислити границю lim ∆у ∆х 0 ∆х. Математична модель (алгоритм) знаходження похідної функції у= f(х)
-
Якщо робите презентацію з різних джерел, то хочаб робіть на одній мові -
-
четко і лаконічно, дякую
Зареєструватись за допомогою Google