Презентація: "Показникові та логарифмічні вирази"
Про матеріал
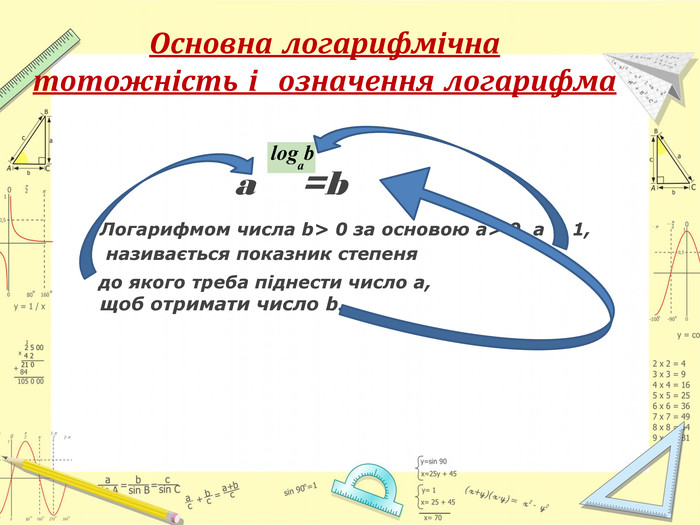
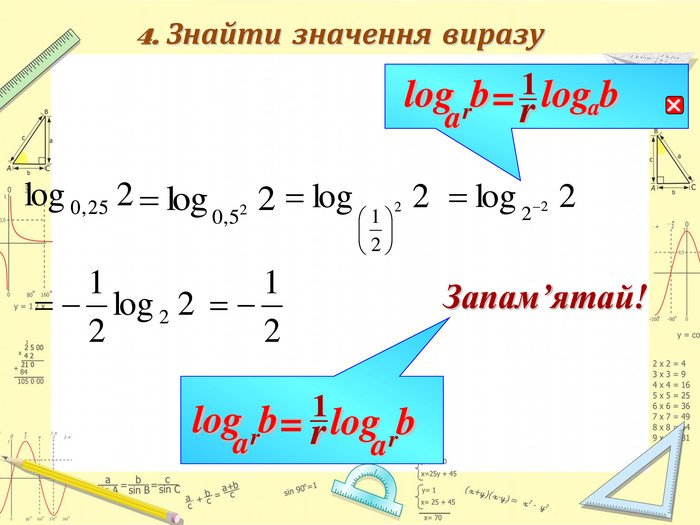
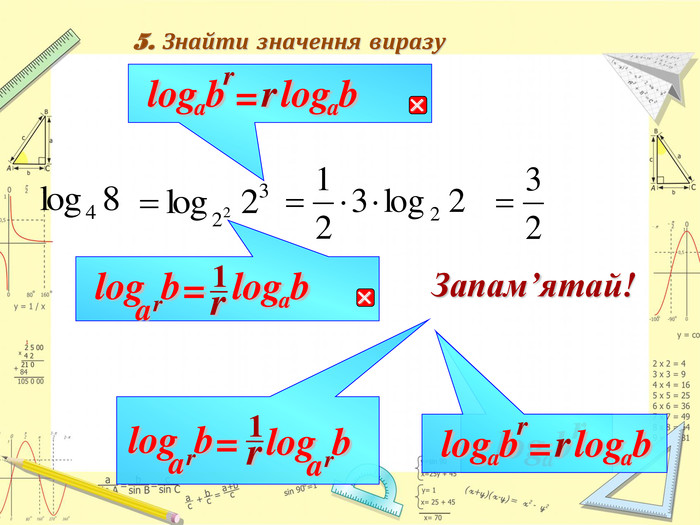
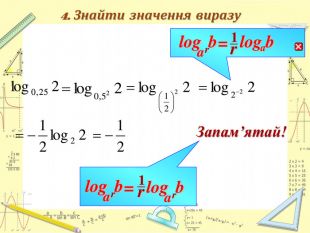
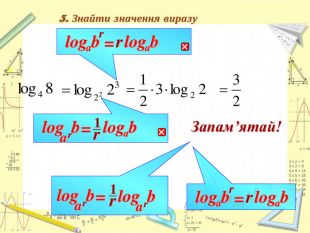
Властивості показникової та логарифмічної функцій. Розв'яування показникових та логарифмічних виразів. Систематизувати відомості про розв’язування показникових та логарифмічних виразів в шкільному курсі алгебри. Розглянула всі основні способи розв’язання показникових та логарифмічних виразів, та всі типові складності які виникають при їх розв’язуванні .
Перегляд файлу
Зміст слайдів


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку