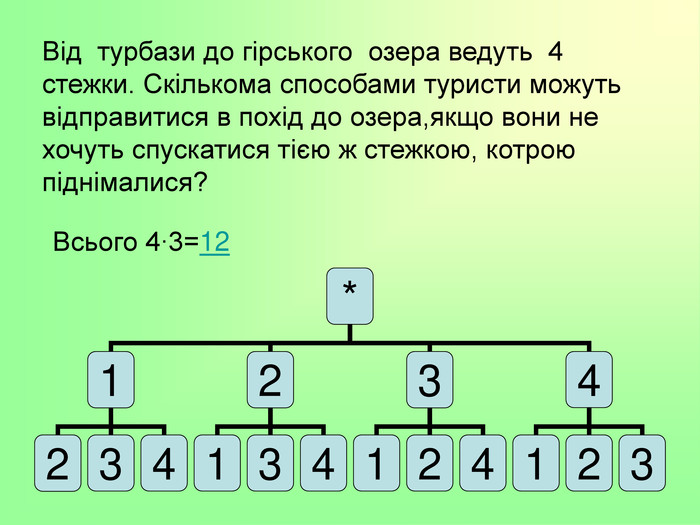
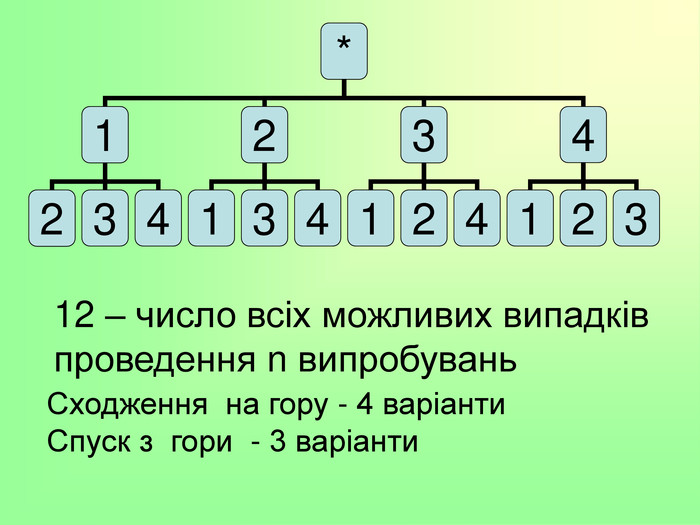
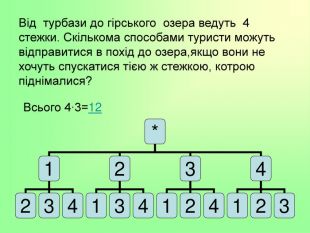
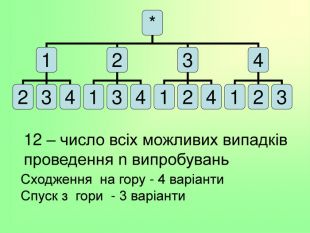
Презентації до теми: "Комбінаторика"
Про матеріал
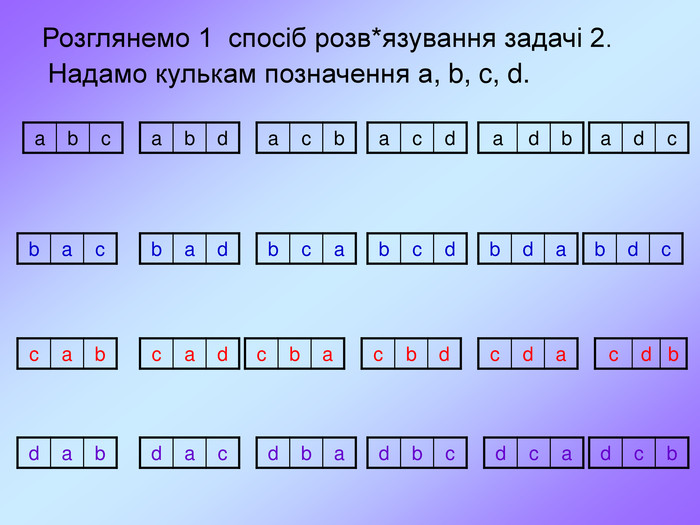
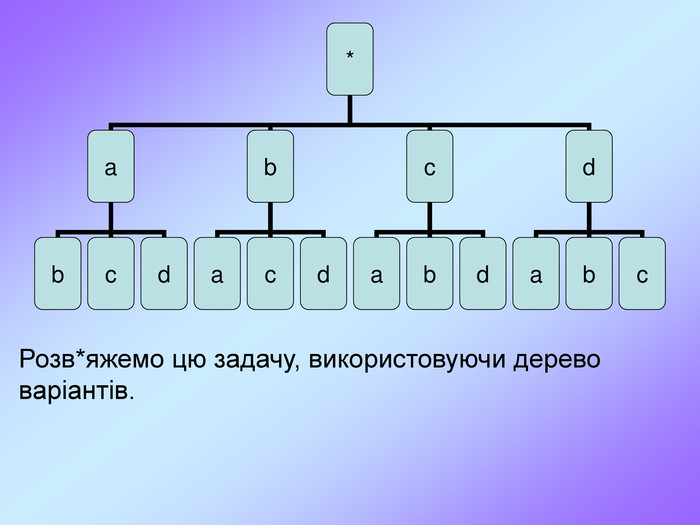
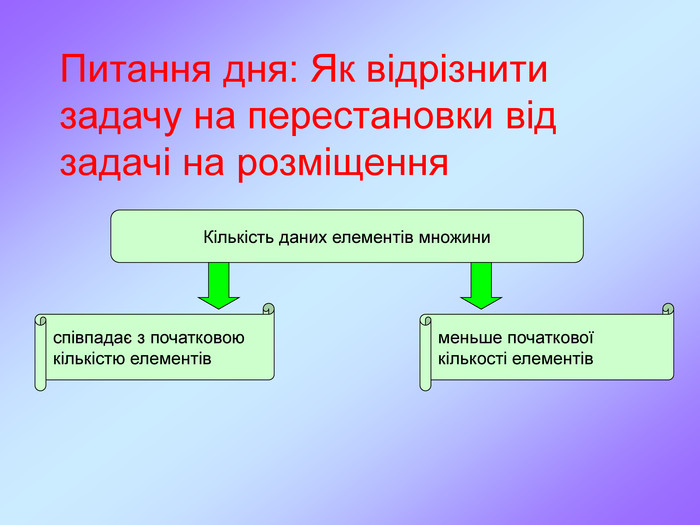
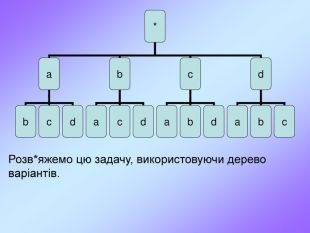
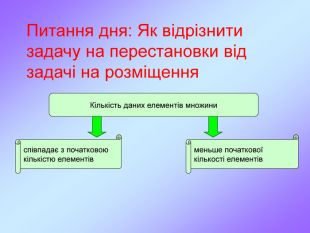
Комбінаторика є важливим розділом математики, що досліджує закономірності розташування, впорядкування, вибору і розподілу елементів з фіксованої множини. При великому числі можливих наслідків випробування способи прямого перебору можливих варіантів малоефективні. На допомогу приходять комбінаторні методи, в основі яких лежать два настутних правила. Перегляд файлу
Зміст слайдів
Перегляд файлу
Зміст слайдів
Перегляд файлу
Зміст слайдів


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку