Конспект уроку "Ромб"

 

 

 

 

План-конспект уроку з геометрії на тему:

«Ромб. Властивості і ознаки ромба»

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Мета уроку: ввести поняття ромб;

навчальна: ознайомити учнів з властивостями й ознаками ромба, сформувати вміння розв’язувати задачі на використання властивостей і ознак ромба;

розвивальна: навчити розпізнавати ромб серед чотирикутників за його ознаками, розв’язувати задачі, використовуючи властивості ромба, розвивати в дітей мислення, логіку і розв’язування задач самостійно;

виховна: виховувати почуття відповідальності за слова і вчинки.

Тип уроку: засвоєння нових знань.

Обладнання: таблиця «Ромб».

 

 

Хід уроку

І. Організаційний етап

Повідомляє учням про тему і мету уроку.

 

ІІ. Перевірка домашнього завдання

Перевірку засвоєння учнями теоретичного матеріалу попереднього уроку можна провести у формі бесіди за питаннями:

1.            Чи є прямокутником паралелограм, один із кутів якого прямий?
2.            Чи правильно, що кожен прямокутник є паралелограмом?
3.            Діагоналі чотирикутника рівні. Чи обов'язково цей чотирикутник є прямокутником?
4.            Діагоналі паралелограма мають довжину 5 см і 7 см. Чи цей парале­лограм є прямокутником?

Після бесіди з учнями, потрібно перевірити письмову частину домашнього завдання.

 

ІІІ. Формулювання теми, мети і завдань уроку

ІV. Актуалізація опорних знань учнів

Пропоную учням накреслити чотирикутник, у якому всі сторони рівні.

Запитання до класу: Чи буде такий чотирикутник паралелограмом? (Так, за ознакою паралелограма)

Звертаю увагу класу на те,що саме цей вид паралелограма й вивчатиметься сьогодні на уроці.

 

V. Вивчення нового матеріалу

План викладання теми

1.               Означення ромба.
2.               Ознаки ромба.
3.               Властивості ромба.
4.               Приклади розв’язування задач із використанням властивостей і ознак ромба.

У ході викладання нової теми складаю таблицю на дошці, а учні в зошитах:

Означення ромба
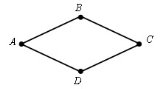
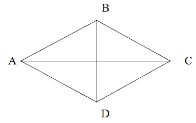
	Ромб – це паралелограм, у якого всі сторони рівні. Ромб – це чотирикутник, у якому всі сторони рівні. Тобто АВ=ВС=СD=DA
Ознаки ромба
		Якщо в паралелограмі діагоналі перетинаються під прямим кутом, то цей паралелограм є ромбом. Тобто АС   BD               Якщо в паралелограмі діагоналі є бісектрисами його кутів, то цей паралелограм є ромбом.               Якщо в чотирикутнику всі сторони рівні,то цей чотирикутник є ромбом.
Властивості ромба
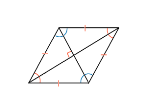
			Протилежні кути рівні. Усі сторони рівні .               Діагоналі точкою перетину діляться навпіл.               Діагоналі ромба перетинаються під прямим кутом.               Діагоналі ромба є бісектрисами своїх кутів.

 

 Означення ромба

Звертає увагу учнів на той факт, що можна використовувати два означення ромба. Дійсно, якщо в чотирикутнику протилежні сторони рівні, то цей чотирикутник – паралелограм за ознакою, а якщо всі його сторони рівні, то цей паралелограм є ромбом.

Ознаки ромба

Разом з учнями переглядають ознаки ромба наведенні в таблиці.

Властивості ромба

Далі наголошую учням, що оскільки ромб – паралелограм, то перші три властивості з таблиці збігаються із властивостями паралелограма.

 

VI. Формування вмінь

Письмові вправи:

Задача № 111

Знайдіть кути ромба, якщо:

А) один із них на 120° більший за інший;

Б) одна з його діагоналей дорівнює стороні.

Розв’язання:

А) Нехай АВСD даний ромб. За властивістю ромба протилежні кути рівні, тобто <А =<C, a <D=<B. Тоді нехай <B позначимо через х, а <A=х+120° .

Також ми знаємо, що <A+<B=180°, тоді маємо рівняння:

х+х+120=180,

х=30.

Отже, <B=<D=30°, a <A=<C=150°.

Відповідь: 30°, 150°, 30°, 150°.

 

Б) Нехай даний ромб АВСD, АС – діагональ ромба АВСD.  Врахувати, що у ромба всі сторони рівні, тому ми отримаємо два рівносторонні трикутники. Отже, тупий кут буде мати 60°, а гострий 120°, так як діагоналі в ромбі є бісектрисами кутів.

Відповідь: 60°, 120°, 60°, 120°.

 

Задача № 120

Знайдіть кути ромба, якщо кути, утворені його стороною з діагоналями, відносяться як 1:4.

Розв’язання:

Нехай дано ромб АВСD, АС і BD – діагоналі,що перетинаються в точці О (мал. 1). За умовою задачі <ABО : <BAО, як 1:4. Тому нехай <ABO=х, а <BAO=4х.

Так як діагоналі ромба перпендикулярні, то розглянемо прямокутний трикутник АВО, де <BOA=90°. З того, що сума кутів трикутника дорівнює 180° отримаємо рівняння:

<ABО + <BAО + <BOA=180°,

Х+4х+ 90=180,

5х=90,

х=18

Отже, <ABO=18°, а <BAO=4*18°=72°.

Так як діагоналі ромба є бісектрисами кутів, то <A=<C=2*<BAO=2*72°=144°, a <B=<D=2*<ABO=36°.

Відповідь: 36° , 144°, 36°, 144°.

 

Задача № 122

З вершини кута ромба, що дорівнює 120°, проведена діагональ завдовжки 6 см. Знайдіть периметр ромба.

Розв’язання:

Нехай дано ромб АВСD, кути А,С – тупі, АС – діагональ ромба АВСD, яка дорівнює 6 см (мал.2 ). За умовою задачі <A=<С = 120°, то <BAC=<BCA=60° (з властивості,що діагональ є бісектрисою), тому можемо знайти <В=180°-<BAC-<BCA  і кут В=60°, отже трикутник АВС рівносторонній. Звідси випливає, що трикутник АСD теж рівносторонній, тобто усі сторони ромба мають по 6 см.

А отже Р=4*6=24 (см).

Відповідь: 24 см.

 

VII. Підсумки уроку

 

Запитання до класу:

1.               Означення ромба.
2.               Чому дорівнює сторона ромба, якщо його периметр становить 32 см?
3.               Що можна сказати про чотирикутник, якщо він є ромбом?
4.               Гострий кут ромба дорівнює 40°. Скільки дорівнює його гострий кут?
5.               Чи може одна з діагоналей ромба дорівнювати його стороні?

 

VIII. Домашнє завдання

Задача № 112.

Задача № 121(а).