Конспект уроку та презентація на тему «Подібність трикутників»

 

 

План – конспект

уроку з геометрії

у 7 класі по темі:

«Ознаки подібності трикутників. Розв'язування задач і вправ»

 

Підготувала

вчитель математики

Михайлівської гімназії

   с. Михайлівка Коростенського району

                                                                        Пашинська Олена Володимирівна

 

Тема. Ознаки подібності трикутників. Розв’язування  задач і вправ.

Мета:

• навчальна:

•      узагальнити, систематизувати знання учнів про зміст та схе­ми застосування означення та ознак подібності трикутників;
•      відпрацю­вати навички застосування набутих знань;

• розвивальна:

•      розвивати розумову діяльність, логічне мислення, слухову та зорову пам’ять, увагу;

• вихована:

•      виховувати позитивне ставлення до математики, працьовитість, кмітливість.

Тип уроку: застосування знань, вмінь і навичок учнів.

Форма проведення: урок-дослідження.

Хід уроку

І. Організаційний момент.

Вчитель. Доброго дня, сідайте за парти. Розкрийте зошити і запишіть сьогоднішню дату і класна робота.

Уявіть собі, що ви пішли зустрічати Новий рік у казковий засніжений ліс. Саме сьогодні справжня зимова пора: усе навкруги вкрито білим пухнастим снігом, сонечко весело всміхається, ніби вже вітає вас із настанням Нового року. Побачивши найвищу ялинку, ви вирішили її прикрасити гірляндами і, головне, яскравою зіркою. Знаючи свої фізичні можливості: піднятися на дерево не вище, ніж 5 м, ви зрозуміли, щоб не витрачати даремно зусиль, потрібно спочатку визначити, чи можливо це зробити.

Проблема? Так! Все наше життя складається з таких маленьких проблем, які ми можемо на сьогоднішній день вирішити, використовуючи ті знання, що отримуємо під час уроків.

 Отже, перед нами стоїть задача – як виміряти висоту ялинки?

 Метою нашого уроку є вчитися застосовувати ознаки подібності трикутників до розв’язування задач. І я сподіваюсь, що в кінці уроку ви зможете вирішити цю проблему.

І почнемо роботу ми  з перевірки домашнього завдання.

ІІ. Перевірка домашнього завдання.

 

 

 

 

 

 

 

 

 

440.

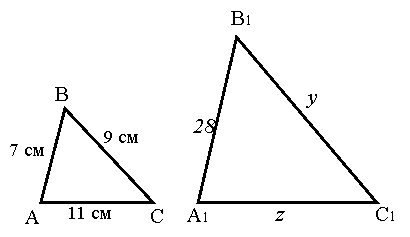Дано: ~

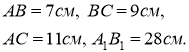Знайти:

 

Розв’язання.

Якщо ~, то відповідні сторони даних трикутників пропорційні , коефіцієнт подібності. Звідси

В-дь: .

447(б).

Розглянемо і (протилежні кути паралелограма), (внутрішні різносторонні при і січній ). Тоді за ознакою подібності подібний . Що й треба було довести.

460.

Дано:

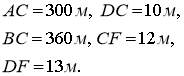
Знайти:

Розв’язання.

Розглянемо : спільний 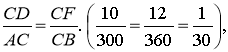тоді за кутом і двома пропорційними сторонами і , звідки: .

В-дь: 390 м.

IІІ. Актуалізація опорних знань.

Вчитель.  Отож, пригадаємо теоретичний матеріал який ми вивчали на попередніх уроках.

Фронтальна бесіда.

1. Які трикутники називаються подібними?
2. Сформулюйте першу ознаку подібності трикутників.
3. Сформулюйте другу ознаку подібності трикутників.
4. Сформулюйте третю ознаку подібності трикутників.
5. Якщо в трикутнику проведено, пряму паралельну третій стороні, то що можна сказати про отримані трикутники?
6. Чи подібні два трикутники, якщо сторони одного трикутника дорівнюють 2 м, 3м і 4м, а другого – 3 м, 4м і 5 м?
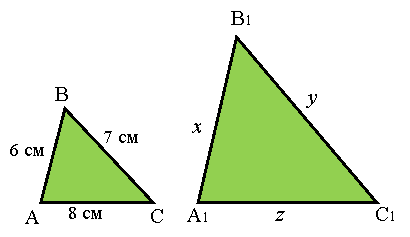
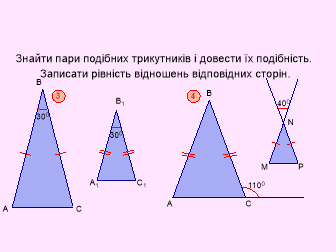
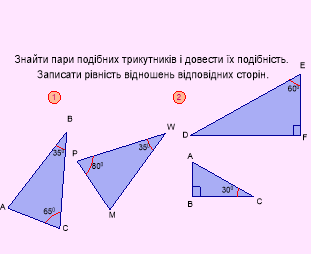
7. Задачі за готовими малюнками:

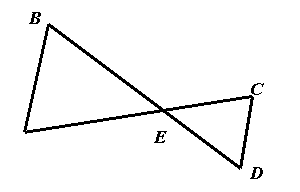
Дано: ~ 

Знайти: .

 

 

 

 

 

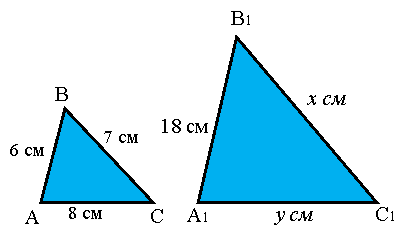
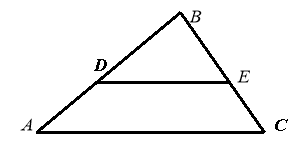
Дано: ~ 

Знайти:

 

 

 

 

 

 

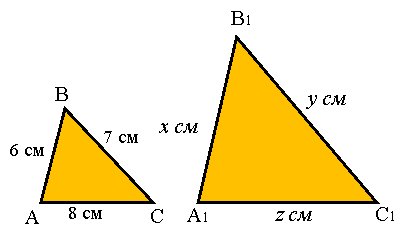
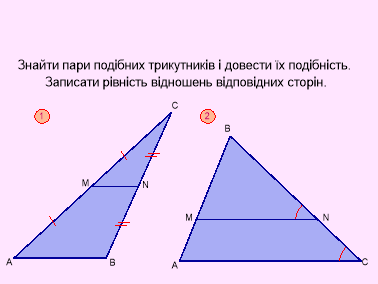
Дано: ~ 

Знайти: .

 

 

 

 

 

 

 

 

 

 

 

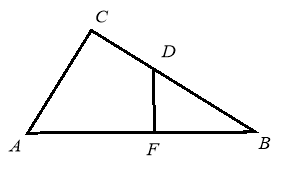
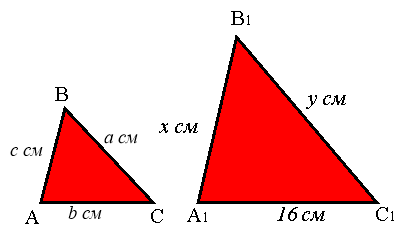
Дано: ~ 

Знайти: .

 

 

 

 

 

 

 

 

 

 

 

 

Вчитель. Ще раз хочу нагадати, що саме узагальнена теорема Фалеса була покладена в основу вивчення подібності фігур, що дало змогу розв’язати багато практичних задач.

Ми не вперше повертаємося на уроках геометрії до імені давньогрецького філософа Фалеса Мілетського,  який говорив: «Блаженство тіла – у здоров’ї, а блаженство розуму – в знаннях».

IV. Розв’язування задач.

1. Завдання  (робота класом).

Задача. Які завбільшки повинні бути букви на класній дошці, щоб учні, сидячи за партами, бачили їх так само виразно, як букви в своїх книжках (на відстані 25см від ока)? Відстань від парт до дошки взяти 5м. Ширина букви в книжці дорівнює 1мм.

Розв’язання

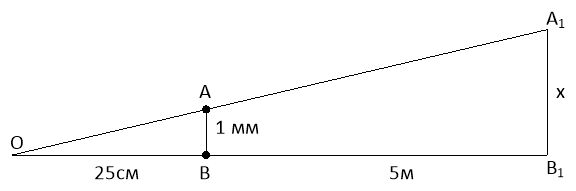
Розглянемо і .спільний, так як - відстань до книжки від читача; - відстань від читача до дошки. , , то .  ~ (за основною теоремою подібності трикутників), звідси

 

 

В-дь: 2,1 см

2. Розв’язуємо задачі в групах.

Завдання для І, ІV груп. З допомогою фотографії виміряти висоту вежі.

Розв'язання.

Висота вежі відноситься до довжини основи так як висота трикутника на фото до основи трикутника. Нехай висота вежі, то

.

В-дь: 28 м.

 

 

 

 

 

 

 

 

 

Завдання для ІІ, V груп. З допомогою фотографії виміряти висоту вежі

 Розв'язання.

 

Висота вежі відноситься до довжини основи так як висота трикутника на фото до основи трикутника. Нехай висота вежі, то

.

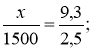
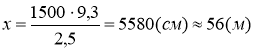В-дь: 56 м.

 

 

 

 

Завдання для ІІІ, VI груп. З допомогою фотографії виміряти висоту вежі

Розв'язання.

 

Висота вежі відноситься до довжини основи так як висота трикутника на фото до основи трикутника. Нехай висота вежі, то

.

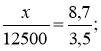
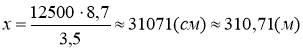В-дь: 310,71 м.

 

 

 

 

 

 

 

Чи можемо ми з вами дати відповідь на поставлене на початку уроку питання: як виміряти висоту ялинки?

   Якщо учні не запропонують цей спосіб, то вчитель розповідає, як це зробити. А саме: у лісі можна знайти будь-яку жердину і ввіткнути її в землю. Дочекатися, коли тінь від ялинки співпаде с тінню від жердини. Тоді ми розглядаємо відношення і знаходимо висоту ялинки.

  До речі, подібна задача була запропонована випускникам на ЗНО у 2009 році. (Рисунок)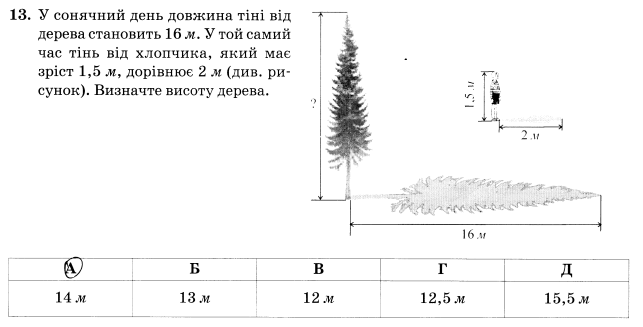

 

 Також існує історичний факт, що Фалес вимірював висоту піраміди за допомогою жердини. Про це можна знайти в довідковій літературі.

V. Діагностика знань та вмінь.

  Пропоную перевірити набуті знання за допомогою тестів.

Варіант 1.

1. Дано: ~. Якщо АВ=12 см, АЕ=8 см, СЕ=6 см, то СD дорівнює:

А 8 см; Б 9 см; В 11см; Г інша відповідь

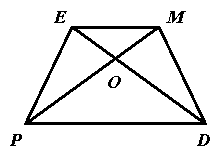2.  Дано: PEMD – трапеція; ~ . Якщо РD=16 см, ОР=10, ОМ=6, то менша основа трапеції ЕМ дорівнює:

А  8,5; Б  10; В  9,6; Г  інша відповідь

3. Прямокутні трикутники АВС і BDС подібні. Якщо АВ=6 см, ВС=18 см, DС=12 см, то ВD дорівнює:

А 8 см; Б 4 см; В 6 см; Г інша відповідь

 4. Дано: ~. Якщо DE=15 дм, DB=20 дм, AD=5 дм, то AC дорівнює:

А 16,5 дм; Б 21 дм; В 18,75 дм; Г інша відповідь

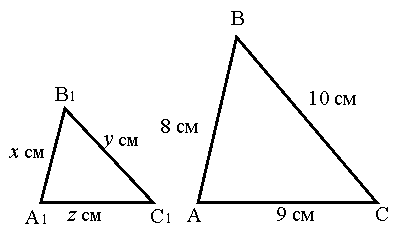5. Дано: ~ . Якщо АВ=8, ВС=9, АС=10 і , то сторони , , відповідно дорівнюють:

А   Б   2;  6;  1; В  1,5;  2,5;  5; Г  інша відповідь

 

 

Варіант 2.

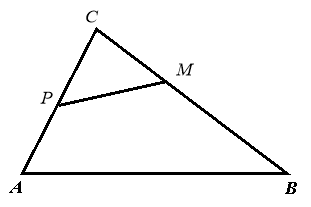1. Якщо 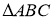~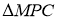, ВС=18 см, СР=6 см, СМ=4 см, то довжина сторони АС дорівнює:

А 6 см;

Б 27 см;

В 12 см;

Г інша відповідь

 

 

2. При перетині діагоналей АС і ВD трапеції АВСD утворюються подібні трикутники ВОС і DОА. Якщо АD=28 см, АО=7 см, СО=5 см, то ВС дорівнює:

 

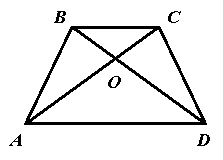
А 14 см;

Б 20 см;

В 18 см;

Г інша відповідь

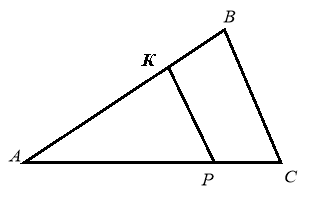
3. Якщо 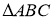~ 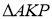і АВ=10, КВ=4, ВС=5, то КР дорівнює:

 

 

 

А  6; Б  3; В  9; Г  інша відповідь

4. Прямокутні трикутники ABC i DBF подібні. Якщо АВ=36 см, СВ=24 см, FВ=12 см, то DB дорівнює:

А 20 см; Б 18 см; В16 см; Г інша відповідь

 

5. Дано: 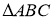~ 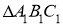. Якщо 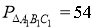см і сторони 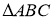дорівнюють АВ=10 см, ВС=9 см, АС=8 см, то сторони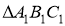 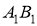, , 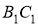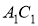відповідно дорівнюють:

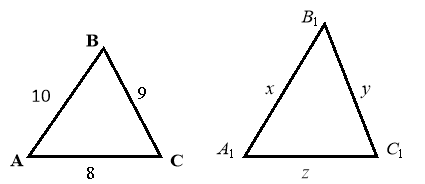А 10 см; 18 см; 8 см; 

Б 5 см; 10 см; 4 см;

В 20 см; 18 см; 16 см;

Г інша відповідь

 

 

  Учні отримують тести. Після розв’язування обмінюються зошитами і перевіряють правильність виконання завдань за допомогою ключа.

V. Підведення підсумків.

 Отже, на початку уроку була запропонована проблемна ситуація, яку ви успішно вирішили під час уроку. Можна зробити висновок, що використовуючи ознаки подібності трикутників ми можемо розв’язати ряд практичних задач.

VI. Домашнє завдання.

Повторити ознаки подібності, впр. 432, 471, 472