Конспект уроку "Властивості степеня з цілим показником" (Урок 1)

Конспект уроку

Алгебра

8 клас

Тема: Властивості степеня з цілим показником.

Мета: домогтися засвоєння учнями властивостей степеня з цілим показником; сформувати вміння відтворювати означення властивостей степеня з цілим показником; навчити розв’язувати вправи на обчислення значень виразів із застосуванням вивчених властивостей степеня з цілим показником.

Тип уроку: вивчення нового матеріалу.

 

Хід уроку

І. Організаційний етап. Оголошення теми уроку. (1хв.)

ІІ. Перевірка домашнього завдання. (5 хв.)

В: Які проблеми виникли у вас при розв’язуванні домашнього завдання? Давайте спробуємо їх вирішити.

Якщо таких учнів 2-4 вчитель просить підійти після уроку і розібратися з проблемами. Якщо ж більше, то вчитель викликає до дошки одного з учнів, у якого виникла проблема.

 

ІІI. Актуалізація опорних знань та вмінь. (5 хв.)

(фронтальне опитування)

В: Як можна записати у вигляді дробу?

У: .

В: А у вигляді степеня?

У: .

В: Чому рівне ?

У: 1.

В: А яка основа степеня повинна бути?

У: а0.

В: Давайте пригадаємо 7 клас, які ви властивості степеня з натуральним показником ви вивчили там?

У: Для будь-якого числа а й довільних натуральних чисел m і n справджується рівність a^maⁿ=a^m+n.

У: Для будь-якого числа а0 й довільних натуральних чисел m і n, де m>n справджується рівність a^m:aⁿ=a^m-n.

У: Для будь-якого числа а й довільних натуральних чисел m і n справджується рівність (a^m)ⁿ=a^mn.

У: Для будь-яких чисел а і b та довільного натурального числа n справджується рівність (ab)ⁿ=aⁿbⁿ.

У: Для будь-яких чисел а та b0 і довільного натурального числа n справджується рівність ()ⁿ=.

 

(усні вправи)

а) (3²)³=3⁶; б) 5²5³=5⁵; в) 2⁴:2²=2²; г) ()²=.

ІV. Вивчення  нового матеріалу. (10 хв.)

В: А як на вашу думку чи будуть ці властивості справедливими для степеня з цілим від’ємним показником?

У: Так.

В: Тоді сформулюйте їх для довільного цілого показника.

У: Для будь-якого а≠0 і будь-яких цілих m i n виконується рівність a^maⁿ=a^m+n

В: Це основна властивість степеня.

У: Для будь-якого а≠0 і будь-яких цілих m i n виконується рівність (a^m)ⁿ=a^mn

У: Для будь-якого а≠0 і b≠0 і будь-якого цілого числа n виконується рівність (ab)ⁿ=aⁿbⁿ.

У: Для будь-якого а≠0 і будь-яких цілих m i n виконується рівність a^m:aⁿ=a^m-n

Для будь-якого а≠0 і b≠0 і будь-якого цілого числа n виконується рівність ()ⁿ=.

 

V. Формування вмінь. (20 хв.)

В: А зараз ми використаємо ці знання для розв’язання вправ.

Один учень розв’язує біля дошки, інші – в себе в зошитах.

№274. (Мерзляк А.Г., Полонський В.Б., Якір М.С.)

Подайте вираз у вигляді степеня або добутку степенів:

1. a^-6a⁹=a^-6+9=a³

Розв’язання: a^-6a⁹=a^-6+9=a³.

3. a^-5a¹⁰a^-12

Розв’язання: a^-5a¹⁰a^-12=a^-5+10-12=a^-7

5. a⁷:a^-3

Розв’язання: a⁷:a^-3=a^7-(-3)=a¹⁰

6) a^-3:a^-15

Розв’язання: a^-3:a^-15=a^-3-(-15)=a¹²

10) (a²)^-4(a^-3)^-2(a^-8)³

Розв’язання: (a²)^-4(a^-3)^-2(a^-8)³=a^-8a⁶:a^-24=a^-8+6-(-24)=a^-8+6+24=a²²

11. (a⁴b^-2c³)^-10

Розв’язання: (a⁴b^-2c³)^-10=a^-40b²⁰c^-30

 

№276. (Мерзляк А.Г., Полонський В.Б., Якір М.С.)

Знайдіть значення виразу:

1. 9⁵9^-7.

Розв’язання: 9⁵9^-7=9^5-7=9^-2=⁼.

3) .

Розв’язання: ==3³=27.

4) .

Розв’язання: ===2.

6) .

Розв’язання: = = = = =1.

8.  .

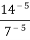Розв’язання: =()^-5=2^-5==.

 

№278. (Мерзляк А.Г., Полонський В.Б., Якір М.С.)

Спростіть вираз:

2).

Розв’язання:  = b^-4-(-5)=b^-4+5=b.

4) .

Розв’язання: ==.

5) .

Розв’язання: = ==, a0, b0.

9) 0,21,5.

Розв’язання: 0,21,5==0,3=0,3, d0.

11).

Розв’язання:  ===.

 

№280. (Мерзляк А.Г., Полонський В.Б., Якір М.С.)

Знайдіть значення виразу:

1) .

Розв’язання:

У:

В: Які основи мають бути, щоб використати якусь з вивчених властивостей?

У: Рівні.

В: Правильно, а ми можемо представити 8 у вигляді степеня з основою 2?

У: 8=.

В: А ?

У: =8==,  2^-9 = .

2) .

Розв’язання:

У: =?

В: А тут яка спільна основа для цих двох степенів?

У: 3.

В: Правильно, а чому?

У: =, 9=. =:====9.

3) 100^-2 :1000^-50,01⁶.

Розв’язання:

У: 100^-2 :1000^-50,01⁶=?

В: А тут, яку візьмемо основу степеня?

У: 10: 100=10², 1000=10³, 0,01== = 10^-2.

100^-2 :1000^-50,01⁶=(10²)^-2 : = ====0,1.

4) (2)^-4-3.

Розв’язання:

У: (2)^-4-3=?

В: Давайте перепишемо перший дріб у вигляді неправильного дробу.

У: 2 = .

В: А у вигляді степеня якогось числа цей дріб можемо записати?

У: = ()².

(()²)^-4-3=()^-8

В: А до якого степеня треба піднести , щоб отримати .

У: -1.    = ()⁹

=()^-8== .

В: А тепер спробуйте самостійно розв’язати.

5) 25^-4(0,2^-3)^-2.

Розв’язання: 25^-4(0,2^-3)^-2=(5²)^-4:=5^-8:()⁶=5^-8:5^-6=5^-8-(-6)= 5^-2== .

 

VI. Підсумки уроку. (3 хв.)

В: Сформулюйте властивості степеня з цілим показником.

 

VII. Домашнє завдання. (1 хв.)