Конспект уроку з алгебри для 10 класу "Метод математичної індукції"

Павлівська загальноосвітня школа I-III ступенів

 

 

 

 

 

  РОЗГОРНУТИЙ КОНСПЕКТ УРОКУ

  з алгебри 10 класу, профільний рівень

  виконав вчитель математики

        Щербак Олександр Сергійович

 

 

 

 

 

 

 

 

 

 

 

       с. Павлівка

   2019

Тема уроку: метод математичної індукції.

Мета уроку: розглянути сутність методу математичної індукції. Навчити      застосовувати його при доведенні деяких тверджень.

Задачі уроку:

Дидактичні:

• забезбечити в ході уроку засвоєння методу математичної індукції;
• сформувати вміння застосовувати цей метод для доведення тотожностей, нерівностей, задач на ділимість, логічних задач.

Виховуючі:

• формування наукового світосприйняття;
• формування інтересу до дослідницької діяльності;
• формування культури мови;
• формування вміння коректно висловлювати точку зору.

Розвиваючі:

• розвиток у школярів вміння виділяти головне, суттєве у досліджуваному матеріалі;
• вміння порівнювати, узагальнювати, логічно висловлювати свої думки;
• формування інтелектуальних відчуттів  (новизни, цікавості, здивування).

Форма проведення уроку:

Урок-лекція, бесіда. Пояснення нового матеріалу.

Матеріально-технічне забезпечення:

дошка, крейда, опорний конспект уроку, підручник для 10 класу, профільний рівень, Є. П. Нелін.

 

 

 

 

 

 

 

 

Хід уроку

 

  ПЛАН ПРОВЕДЕННЯ УРОКУ

1. Актуалізація знань. (5хв.)
2. Основна частина уроку.(15хв.)
3. Закріплення матеріалу. (17хв.)
4. Підведення підсумків уроку. (5 хв.)
5. Домашнє завдання. (3 хв.)

 

 

1. Актуалізація знань.

Запитання вчителя (усно):

а) Наведіть приклади тверджень.

б) Які різновиди тверджень ви знаєте?

(загальні і часні).

в) Наведіть приклади загальних тверджень.

г) Наведіть приклади часних тверджень.

При вивченні явищ в любій галузі знань – математики чи історії, фізики чи медицини, астрономії чи економіки, всюди і завжди основним етапом є встановлення певних закономірностей, пов’язуючих окремі елементи вивчаємого явища. Ми знаходимо певний зв’язок між елементами вивчаємого явища, справедливого для багатьох часних випадків, потім розповсюджуєм на всі випадки взагалі, встановлюючи таким чином загальний закон, що розкриває сутність даного явища.

Всі твердження можно поділити на загальні та часні. Наприклад, твердження «У будь-якого паралелограма діагоналі діляться точкою перетину навпіл» є загальним, так як відноситься до всієї множини паралелограмів. У той же час твердження «У паралелограмі ABCD діагоналі діляться точкою перетину навпіл», є часним, так як відноситься до конкретного паралелограма ABCD.

На основі часних тверджень роблять деякі припущення (гіпотези) про справедливість якого-небудь твердження. Інколи ці припущення видаються вірними, інколи помилковими.

2. Основна частина уроку.

Відомий математик 17 століття Пьєр Ферма висунув припущення, що простими є всі числа виду .Він показав, що перші п’ять чисел

, , , , =65537 – прості і робить по індукції припущення, що для всіх n чисел виду –  прості.

Однак це припущення виявилось не вірним, так як у 18 столітті Л.Ейлер знайшов, що 2²⁵+1=4294967297=641∙6700417 – складене число.

  Таким чином, індукція не є методом доведення, а лише допомагає сформулювати невідомий результат у вигляді деякої гіпотези, справедливість якої потім треба довести.

Більшість властивостей чисел спочатку були відкриті шляхом спостережень, задовго до того, як істинність була строго доведена.

Джузеппе Пеано показав, що для дедуктивної побудови арифметики натуральних чисел достатньо чотирьох аксіом. Так аксіома 4 у нього говорить:  Якщо яка-небудь теорема про властивості натруальних  чисел доводить для одиниці і якщо із допущення, що вона вірна для натурального числа і, слідує, що вона вірна для всіх натуральних чисел.

Перехід від часних тверджень до загальних називають індукцією (від латинського слова inductio – спрямування).

Принцип математичної індукції полягає в наступному:

Твердження P(n) справедливе для  будь-якого натурального n, якщо:

1. Воно справедливе для n=1 або для найменшого з натуральних чисел, при якому закономірність має сенс.
2. Із справедливості твердження, для якого-небудь довільного натурального n=k, слідує його справедливість для n=k+1.

Саме доведення методом математичної індукції складається з наступних частин:

1. Перевіряють справедливість гіпотези для найменшого з натуральних чисел, при якому гіпотеза має сенс (базис).
2. Зробивши припущення, що гіпотеза вірна для деякого значення k, прагнуть довести справедливість її для k+1.
3. Якщо таке доведення вдалося довести докінця, то, на основі принципу математичної індукції можна стверджувати, що висловлена гіпотеза справедлива для любого натурального числа n.

3. Закріплення матеріалу.

ПРИКЛАД 1. Довести твердження:

 

РОЗВ’ЯЗОК

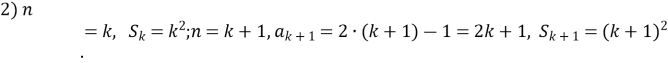
Необхідно довести що

 

 

ПРИКЛАД 2. Довести, що , при

РОЗВ’ЯЗОК

Доведемо твердження для :

 

ПРИКЛАД 3.  Кожна людина у світі потисла якусь кількість рук. Доведіть, що число людей, потиснувших непарне число рук – парне.

РОЗВ’ЯЗОК

Пронумеруємо всі рукостискання у світі від першого до довільного натурального n.

При n=1, можливі варіанти: 2, 4 або 0 рукостискань, тобто твердження задачі виконується.  Припустимо, що воно вірне при деякому  n=k, тобто кількість людей, що приймала участь у рукостисканнях з номерами від 1 до k і зробивших непарну кількість рукостискань, парна.

Доведемо справедливість цього твердження для n=k+1, можливі три варіанти здійснюється k+1 рукостискань: одна одній тиснуть руки:

• дві особливі людини;
• дві неособливі людини;
• одна особлива і одна неособлива людина.

В кожному з цих трьох випадків кількість особливих людей або зменшується на два, або збільшується на два, або не змінюється.

Твердження доведене.

ПРИКЛАД 4. Методом математичної індукції доведіть справедливість рівності: (за підручником с. 35 №1)

 

ДОВЕДЕННЯ

Доведемо що

ПРИКЛАД 5. Методом математичної індукції доведіть справедливість рівності: (за підручником с. 35 №2)

Доведемо що

 

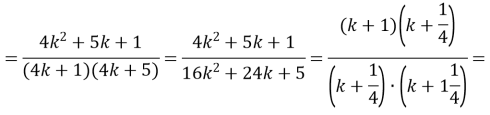
ПРИКЛАД 6. Методом математичної індукції доведіть справедливість рівності: (за підручником с. 35 №3)

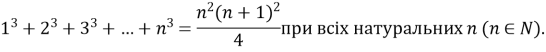
ДОВЕДЕННЯ

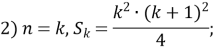
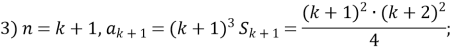
Доведемо що

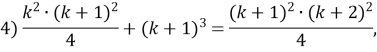
Ділимо обидві частини на :

 

ПРИКЛАД 7.

Методом математичної індукції доведіть справедливість рівності: (за підручником с. 35 №5)

ДОВЕДЕННЯ

Доведемо що

ПРИКЛАД 8. Доведіть, що n³- n ділиться на 3 при будь-якому натуральному значенні n.

ДОВЕДЕННЯ

Припустимо що , перевіримо дане твердження для

що і потрібно було довести.

ПРИКЛАД 9. Доведіть нерівність за допомогою методу математичної індукції: (за підручником с. 35 №6).

якщо

 

ДОВЕДЕННЯ

припустимо що нерівність виконується при n=k:

помножимо нерівність 2) на 4, отримуємо:

щоб отримати подібний вираз, додамо  та віднімемо від нерівності 3)

вираз

що і потрібно було довести  (вираз за припущенням, а

оскільки k>1).

ПРИКЛАД 10.  Доведіть, що любе ціле число гривень, більше від 7, можна сплатити без здачі грошовими білетами вартістю в 3 і 5 гривень.

ДОВЕДЕННЯ

1.  Для 8 гривень рівність справедлива (оскільки 3+5=8).
2.  Нехай твердження вірне для k гривень, де k – ціле число, більше або дорівнює 8.

Можливі два випадки: а) k гривень сплачуються одними трьохгривневими білетами і b) k гривень сплачуються грошовими білетами, серед яких є хоч один  білет п’ятигривневої вартості.

У першому випадку трьохгривневих білетів повинно бути не менше трьох, так як в цьому випадку k>8. Для того, щоб сплатити k+1 гривню, замінимо три трьохгривневих білета двома п’яти гривневими.

У другому випадку для сплати k+1 гривень замінимо один п’ятигривневий білет двома трьохгривневими.

4. Підведення підсумків уроку.

Вчитель задає запитання учням:

• Що таке метод математичної індукції і яке його призначення?

5. Домашнє завдання.

Вчитель записує завдання на дошці.

Вивчити теоретичний матеріал, розв’язати завдання:

• за підручником: с.35 №4, №7;
• додаткове завдання (на 12 балів):

доведіть, що сума кубів трьох послідовних натуральних чисел ділиться на 3.

Розв’язання

с.35 №4

Методом математичної індукції доведіть справедливість виразу:

ДОВЕДЕННЯ

Доведемо що

с.35 №7

Методом математичної індукції доведіть нерівність:

Припустимо, що нерівність виконується при :

Помножимо нерівність 2) на 2 і перенесемо всі змінні вліво:

До нерівності 3) додамо та віднімемо , і перенесемо всі змінні вліво:

що і потрібно було довести.

(Вираз

оскільки за умовою а оскільки дана функція завжди додатна).

Завдання №3

Довести що при будь-якому натуральному n.

Припустимо, що твердження виконується для

тоді вираз 3) матиме вид:

де

за припущенням, а у вираза спільний множник 9. Твердження доведене.