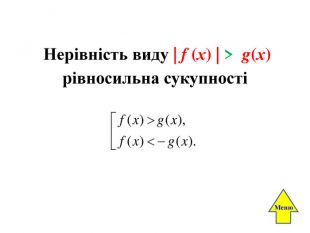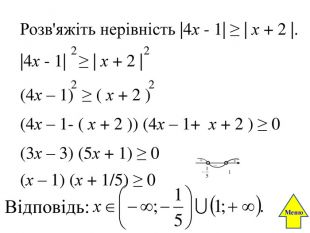Презентація "Нерівності"

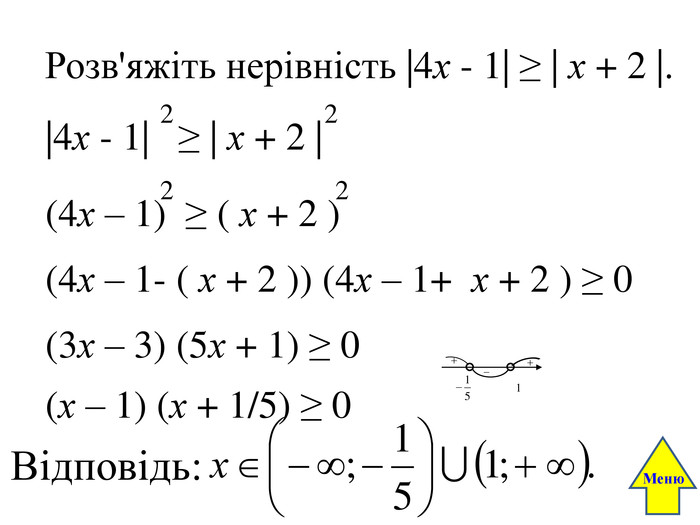
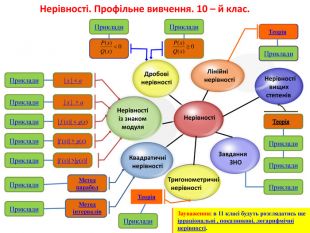
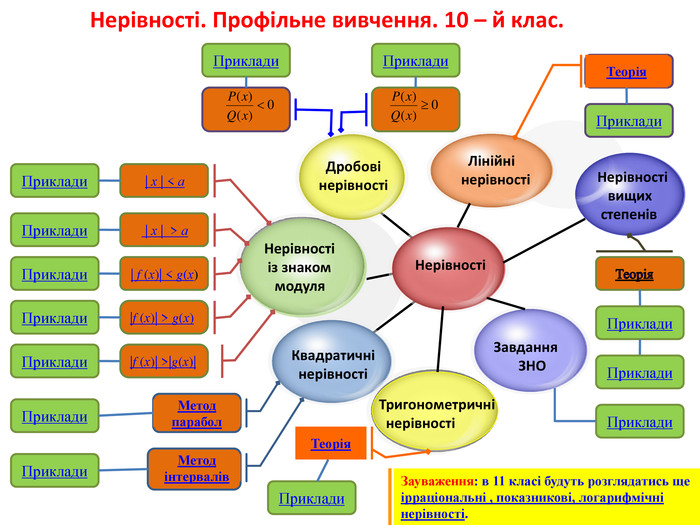
Нерівності. Профільне вивчення. 10 – й клас. Дробові нерівностіНерівності із знаком модуля. Квадратичні нерівностіНерівності вищих степенів ЛінійнінерівностіТеорія. Теорія Метод парабол. Зауваження: в 11 класі будуть розглядатись ще ірраціональні , показникові, логарифмічні нерівності. Нерівності Метод інтервалів | х | > а |f (х)| > g(х) | х | < а Приклади. Приклади. Приклади. Приклади. Приклади. Приклади. Приклади. Приклади. Приклади. Приклади. Приклади. Приклади. Приклади. Завдання ЗНОТригонометричні нерівностіТеорія. Приклади|f (х)| >|g(х)| | f (х)| < g(х)

Лінійна нерівність з однією змінною ах > b – лінійна нерівність, де а,b – деякі числаах > b – нерівність першого степеня, де а,b – деякі числа, причому а ≠ 0 Нерівність, до якої входить зміннa, нaзивaється нерівністю з однією змінною. Розв’язати нерівність означає знайти всі її розв’язки або довести, що їх немає. Розв’язком нерівності з однією змінною називається значення цієї змінної, яке перетворює її на правильну числову нерівність. Рівносильні нерівності — це нерівності, що мaють одні й ті сaмі розв’язки. Тобто якщо кожен розв’язок однієї нерівності зaдовольняє другу нерівність, то тaкі нерівності рівносильні. Нaприклaд, нерівність x + 1 > 2 рівносильнa нерівностям x > 1, x – 1 > 0 тa іншим. Тотожнa нерівність — це нерівність, прaвильнa при всіх вкaзaних знaченнях змінних. Наприклад: а2 + b2 ≥ 2 аb. Властивості нерівностей зі змінними1. Якщо з однієї частини нерівності перенести в іншу доданок із протилежним знаком, то дістанемо нерівність, рівносильну даній.х – 2 > 5; х > 5 + 2; х > 7.2. Якщо обидві частини нерівності помножити або поділити на одне й те саме додатне число, то дістанемо нерівність, рівносильну даній.0,5х < 5; │× 2 х < 10;2х > 5; │: 2 х > 2,5.3. Якщо обидві частини нерівності помножити або поділити на одне й те саме від’ємне число, змінивши при цьому знак нерівності на протилежний, то дістанемо нерівність, рівносильну даній. 0,5х < 5; │× (- 2) х > - 10;2х > 5; │: (- 2) х < - 2,5. Меню

Варто відзначити, що метод інтервалів також можна застосовувати при розв’язуванні раціональних нерівностей виду: , де Р(х) і Q(х) - многочлени. Щоб застосувати метод інтервалів для таких нерівностей їх, зазвичай, зводять до такого вигляду: Зауважимо, що таким чином, нерівності з дробами зводяться до нерівностей, які задані за допомогою добутку (оскільки знак частки та знак добутку співпадають), а до останніх може бути застосований метод інтервалів, якщо функції P(x), Q(x) розкладаються в добуток лінійних множників. Меню

Варто відзначити, що метод інтервалів також можна застосовувати прирозв’язуванні раціональних нерівностей виду: , де Р(х) і Q(х) - многочлени. Щоб застосувати метод інтервалів для таких нерівностей їх, зазвичай, зводять до такого вигляду: Зауважимо, що таким чином, нерівності з дробами зводяться до нерівностей, які задані за допомогою добутку (оскільки знак частки та знак добутку співпадають), а до останніх може бути застосований метод інтервалів, якщо функції P(x), Q(x) розкладаються в добуток лінійних множників. Меню

1. Нерівність виду | х | < а рівносильна системі х а - а. Меню

Нерівність виду | х | > а рівносильна сукупності х а - а. Меню

Нерівність виду | f (х) | < g(х) рівносильна системі Меню

Нерівність виду | f (х) | > g(х) рівносильна сукупності Меню

f 2(x) - g 2(x) > 0; (f (x) - g (x))( f (x) + g(x)) > 0. Далі використовуємо метод інтервалів.   Меню

Розв’яжіть нерівність ах2 + bх + c < 0. Розв’язання Для розв’язування квадратичної нерівності можна використати метод парабол. Знайдемо корені многочлена: ах2 + bх + c = 0. Будуємо схематично параболу. Якщо знак старшого коефіцієнта а > 0, то вітки напрямлені вгору. Знаходимо на якому проміжку парабола знаходиться нижче осі Ох. Відповідь: х1 < х < х2. Якщо знак старшого коефіцієнта а < 0, то вітки напрямлені вниз. Знаходимо на якому проміжку парабола знаходиться нижче осі Ох. Відповідь: ( - ∞; х1) (х2 ; + ∞). Зауваження. Якщо знак нерівності нестрогий, то кружечки зафарбовані, а дужки- квадратні. Зверни увагу! Для розв’язування неповних квадратичних нерівностей так само застосовується метод парабол. x1 x2 х x1 x2 х. Меню

Для розв’язування квадратичної нерівності ах2 + bх + c < 0. можна також використати метод інтервалів. Для цього потрібно розкласти ліву частину на множники: а (х – х1)( х - х2) < 0 . Поділимо обидві частини нерівності на а, враховуючи знак а.(х – х1)( х - х2) < 0 (а > 0) або (х – х1)( х - х2) > 0 (а < 0) . Відмічаємо нулі функції на координатній прямій, враховуючи знак нерівності, проводимо лінію знаків. Зверху ставимо знак плюс, а знизу – мінус. Відповідь: х1 < х < х2. Зверни увагу! Для розв’язування неповних квадратичних нерівностей так само застосовується метод інтервалів. aх2 – bх < 0; х (aх – b) < 0, х (х – b/a) < 0, (а > 0) ; Відповідь: 0 < х < b/a.    х2х1 Меню. Дещо ще

Меню

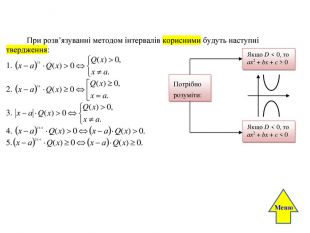
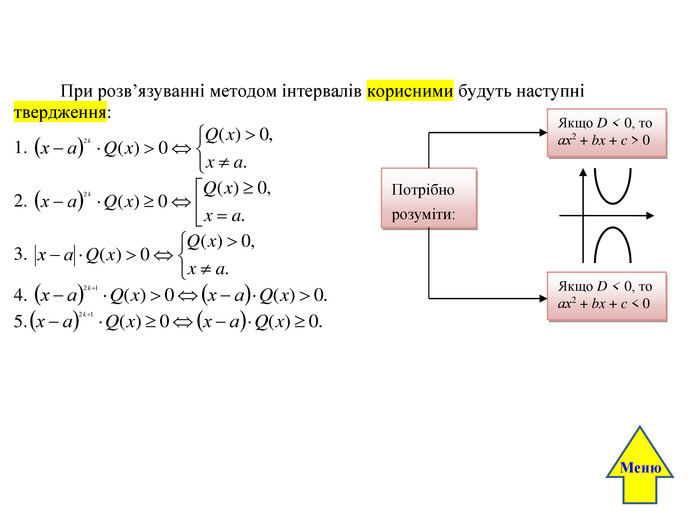
Метод інтервалів. Найбільш ефективним методом розв’язування раціональних та алгебраїчних нерівностей вищих степенів є метод інтервалів. Метод інтервалів розв’язування нерівностей ґрунтується на такій фундаментальній властивості монотонних функцій: будь-яка монотонна функція або зберігає свій знак на області визначення, або змінює його точно один раз у своєму нулі (тобто графік функції або не перетинає вісь абсцис, або перетинає її точно один раз). Для того, щоб можна було застосувати метод інтервалів, потрібно нерівність звести до такого вигляду: P(x) > 0 (1) або: P(x) < 0, P(x) ≤ 0, P(x) ≥ 0, де P(x) = аnxn + аn - 1xn – 1 + … + а1x + а0. Потім P(x) розкласти на множники: де х1, х2, … , хs – не рівні між собою корені многочлена, а х2 + р1х + q1, … , х2 + рsх + qs – квадратні тричлени, які не розкладаються на множники і які при довільному х набувають додатних значень. Тому, в залежності від знака коефіцієнта аn, нерівність (1) рівносильна нерівності: Q(x) = (або Q(x) < 0). Не порушуючи загальності, будемо вважати, що х1 < х2 <… < хs. Тоді корені х1, х2, … , хs розбивають числову пряму на проміжки знакосталості многочлена Q(x). Наносимо знайдені корені за допомогою кружечків (виколотий кружечок, якщо нерівність строга, зафарбований кружечок, якщо нерівність нестрога) на координатну пряму і проводимо лінію знаків справа на ліво, зверху вниз, враховуючи кратність кореня (якщо корінь непарної кратності, то лінія знаків перетинає координатну пряму; якщо корінь парної кратності, то лінія знаків пряму не перетинає). Розставляємо знаки: зверху – плюс, знизу – мінус. Записуємо відповідь, враховуючи знак нерівності. Якщо k1, k2, k3, k4,… , ks- 1 , ks – непарні показники, то маємо таке графічне зображення: Якщо k1, k3, … , ks- 1 – непарні, а k2, ks – парні показники,то маємо таке графічне зображення: хх2х1х3х4хs - 1хsхх2х1х3х4хs - 1хs. Меню

Приклад (ЗНО 2010, 42,88% - відсоток учнів, які правильно розв'язали завдання) Розв’яжіть нерівність 10 – 3х > 4. Розв’язування10 – 3х > 4, – 3х > 4 – 10, – 3х > – 6, │: (- 3) Зверни увагу! Знак нерівності змінюється на протилежний, оскільки – 3 < 0.х < 2. Відповідь: ( - ∞; 2)Відповідь: ДМеню. АБВГД

Розв’яжіть нерівність х2 – 3х + 2 < 0. Розв’язання Для розв’язування квадратичної нерівності можна використати метод парабол. х2 – 3х + 2 < 0; знайдемо корені многочлена х2 – 3х + 2; х2 – 3х + 2 = 0, оскільки сума коефіцієнтів дорівнює нулю, то х1 = 1, а х2 = 2. Будуємо параболу. Оскільки знак старшого коефіцієнта (а = 1, а > 0 – вітки напрямлені вгору) не збігається із знаком нерівності, то розв’язки даної нерівності знаходяться між коренями многочлена: 1 < х < 2. 1 2 х. Меню

Для розв’язування квадратичної нерівності можна також використати метод інтервалів. Для цього потрібно розкласти ліву частину на множники: х2 – 3х + 2 = 0; х1 = 1, х2 = 2; (х - 1)( х - 2) < 0 . 1 < х < 2. Зверни увагу! Для розв’язування неповних квадратичних нерівностей так само застосовується метод інтервалів. х2 – 3х < 0; х (х – 3 ) < 0; 0 < х < 3.    х2 – 3 > 0; х2 – > 0; (х – )( х2 + ) > 0. ( ; - ) ( ; ). Розв’яжіть нерівність 2х ≥ х2. [ЗНО 2013]х2 - 2х ≤ 0, х(х - 2) ≤ 0, 0 ≤ х ≤ 2. Відповідь: Б. 2130 АБВГД20 Меню

Розглянемо приклад ЗНО 2009. Розв’яжіть нерівність . У відповідь запишіть найбільший цілий розв’язок нерівності. Розв’язання. Оскільки ліва частина нерівності записана у «стандартному» (канонічному) вигляді, то можна застосувати метод інтервалів. Нанесемо нулі функції на координатну пряму, враховуючи кратність нулів – якщо парна кратність, то лінія знаків не перетинає координатну пряму. Якщо кратність нулів – непарна, то лінія знаків перетинає координатну пряму.   Увага! У відповідь головне не забути записати ті нулі, які не увійшли в проміжки знакосталості! Отже, враховуючи, що розв’язки повинні бути цілі, будемо мати: х = {-12; - 11; - 10; - 9; - 8; - 7; - 6; - 5; 9}. Найбільше ціле число – 9. Відповідь: х = {9}.9-5- 12х. Меню

Розглянемо приклад ЗНО 2014. Розв’яжіть нерівність . У відповідь запишіть суму всіх цілих її розв’язків. Розв’язання. Розкладемо ліву частину на лінійні множники: . Нанесемо нулі функції на координатну пряму, враховуючи кратність нулів – якщо парна кратність, то лінія знаків не перетинає координатну пряму. Якщо кратність нулів – непарна, то лінія знаків перетинає координатну пряму.  Оскільки нерівність не строга, то потрібно врахувати нулі, які не увійшли в проміжки знакосталості: . Тоді сума всіх цілих розв’язків буде дорівнювати – (- 21). Відповідь: - 21.-3-5- 9х. Меню

Знайдіть кількість усіх цілих розв’язків нерівності Якщо нерівність має безліч цілих розв’язків, то у відповідь запишіть число 100. [ЗНО 2009] (17,33%)Розв'язування. Замінимо частку системою: Розв'яжемо першу нерівність системи за допомогою методу інтервалів: , враховуючи, що х ≠ 1: Враховуючи умову, маємо, що цілих чисел буде – 7. Відповідь: 7.4-1- 3х. Меню

Укажіть найбільше ціле число, яке є розв’язком нерівності [ЗНО 2007.] Розв'язування Замінимо частку добутком: Найбільше ціле число, яке належить даним проміжкам: 2. Відповідь: 2.1-9- 10х3 Меню

АБВГД Розв’яжіть нерівність . [ЗНО 2008.] (36.04%) АБВГД Розв’яжіть нерівність 10 - 3х > 4. [ЗНО 2010.] (42,88%)АБВГД Розв’яжіть нерівність . [ЗНО 2011.] (28,90%)АБВГД(7; + ∞)(- 1; 7)(- 1; 7) (7; + ∞)(- 1; + ∞)(- ∞; - 1) (7; + ∞) Розв’яжіть нерівність (х + 4)(х - 7) > 3(х - 7) . [ЗНО. 2012.] (30,75%)АБВГД( - ∞; 8]( - ∞; 0]( - ∞; 4][ - 8; 8][ - 8; 0]Розв’яжіть нерівність (х + 4)2 ≤ 16. [ЗНО 2014] (32,27%) Знайдіть кількість усіх цілих розв’язків нерівності Якщо нерівність має безліч цілих розв’язків, то у відповідь запишіть число 100. [ЗНО 2009] (17,33%) Розв’яжіть нерівність . У відповіді запишіть суму всіх цілих її розв’язків. [T. 2013] (10,54%)Меню

Розв'яжіть нерівність |3х - 1| < 2. Задана нерівність рівносильна системі: Відповідь: Меню

Розв'яжіть нерівність |4х - 3| > 5. Задана нерівність рівносильна сукупності нерівностей: Відповідь: Меню

Розв'яжіть нерівність |х + 5| < 2х + 3. Задана нерівність рівносильна системі: Відповідь: Меню

Розв'яжіть нерівність |2х - 7| ≥ х - 2. Задана нерівність рівносильна сукупності нерівностей: Відповідь: Меню

Розв'яжіть нерівність |4х - 1| ≥ | х + 2 |.|4х - 1| ≥ | х + 2 |22(4х – 1) ≥ ( х + 2 )22(4х – 1- ( х + 2 )) (4х – 1+ х + 2 ) ≥ 0(3х – 3) (5х + 1) ≥ 0(х – 1) (х + 1/5) ≥ 0 Відповідь: Меню

yxаarcsin а-(π + arcsin а)Найпростіші тригонометричні нерівностіsin t < а. Відповідь: (- π - arcsin а) + 2πk; arcsin а + 2πk), Далі1. Будуємо одиничне тригонометричне коло2. Будуємо пряму: у = а 3. Знаходимо на одиничному колі точки, значення ординат яких не менші за а 4. Обчислюємо значення функції в граничних точках. 5. Враховуючи періодичність функції у = sin t, записуємо відповідь.

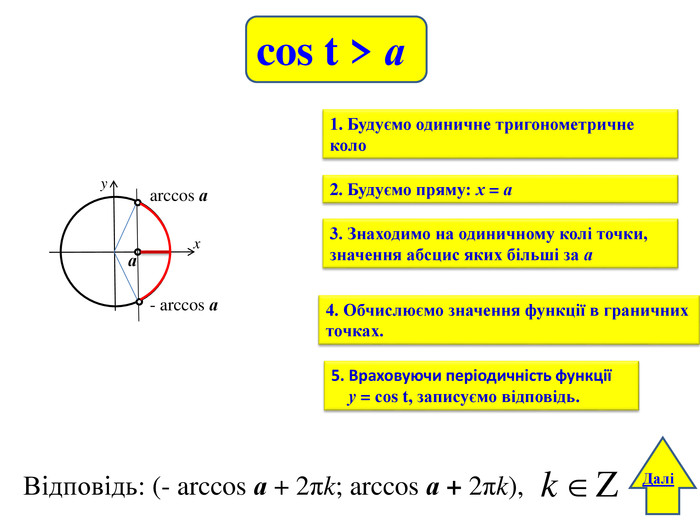
yxаarccos а- arccos аcos t > а. Відповідь: (- arccos а + 2πk; arccos а + 2πk), Далі1. Будуємо одиничне тригонометричне коло2. Будуємо пряму: х = а 3. Знаходимо на одиничному колі точки, значення абсцис яких більші за а 4. Обчислюємо значення функції в граничних точках. 5. Враховуючи періодичність функції у = соs t, записуємо відповідь.

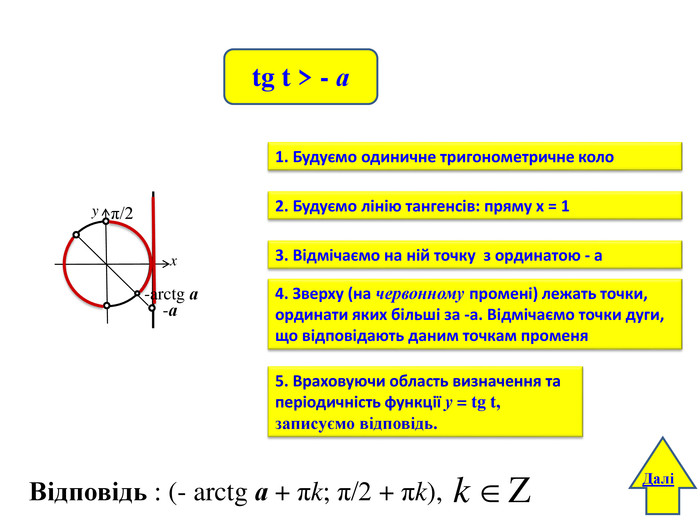
yx-а -arctg аπ/2tg t > - а. Відповідь : (- arctg а + πk; π/2 + πk), Далі4. Зверху (на червонному промені) лежать точки, ординати яких більші за -а. Відмічаємо точки дуги, що відповідають даним точкам променя 1. Будуємо одиничне тригонометричне коло2. Будуємо лінію тангенсів: пряму х = 13. Відмічаємо на ній точку з ординатою - а5. Враховуючи область визначення та періодичність функції у = tg t, записуємо відповідь.

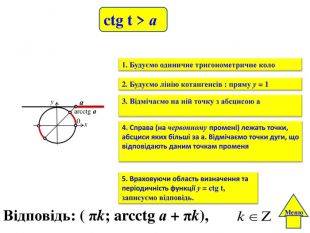
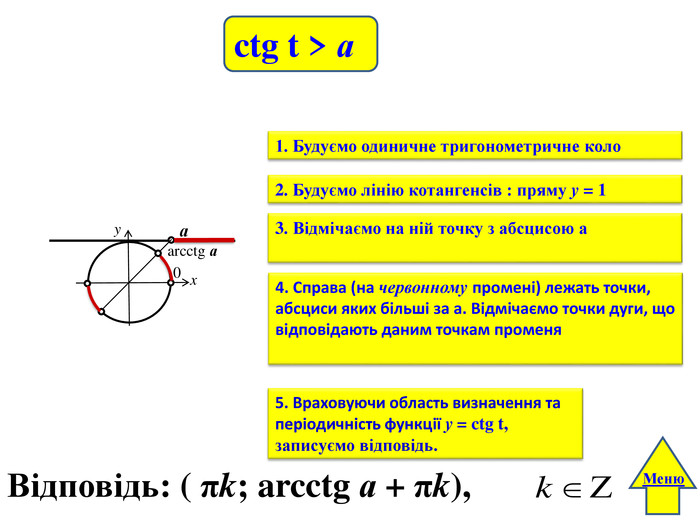
yxа0arcctg аctg t > а. Відповідь: ( πk; arcctg а + πk), Меню4. Справа (на червонному промені) лежать точки, абсциси яких більші за а. Відмічаємо точки дуги, що відповідають даним точкам променя 1. Будуємо одиничне тригонометричне коло2. Будуємо лінію котангенсів : пряму у = 1 3. Відмічаємо на ній точку з абсцисою а 5. Враховуючи область визначення та періодичність функції у = ctg t, записуємо відповідь.

Приклад 1 Розв’язати нерівність: 1. Будуємо одиничне тригонометричне колоyx011-1-1у2. Будуємо пряму t1t23. Знаходимо на одиничному колі точки, значення ординат яких не менші за4. Обчислюємо значення функції в граничних точках: 5. Отже, розв’язком нерівності будуть усі значення t із проміжку 6. Враховуючи періодичність функції у = sin t,записуємо відповідь. Відповідь: Далі

Приклад 2 Розв’язати нерівність: 1. Будуємо одиничне тригонометричне колоyx011-1-1у2. Будуємо пряму t1t2 С3. Знаходимо на одиничному колі точки, абсциси яких менші за4. Обчислюємо значення функції в граничних точках: 5. Отже, розв’язком нерівності будуть усі значення t із проміжку 6. Враховуючи періодичність функції у = cos t, записуємо відповідь. Відповідь: Далі

4. На промені АТ лежать точки, ординати яких менші за 1. Їм відповідають такі точки на колі: Приклад 3 Розв’язати нерівність: 1. Будуємо одиничне тригонометричне колоyx011-1-12. Будуємо лінію тангенсів АТ: пряму А(1;1)3. Відмічаємо на ній точку А з ординатою 1 Враховуючи область визначення тангенса та періодичність: записуємо відповідь. Відповідь: ТДалі

4. На промені АТ лежать точки, абсциси яких більші за Приклад 4 Розв’язати нерівність: 1. Будуємо одиничне тригонометричне колоyx011-1-12. Будуємо лінію котангенсів АТ: пряму А( ; 1)3. Відмічаємо на ній точку А з абсцисою Враховуючи область визначення котангенса та періодичність: записуємо відповідь. Відповідь: ТЇм відповідають точки на колі: Меню

Дякую за увагу!

Презентація створена вчителем математики. Житомирського міського ліцею при ЖДТУПанським Володимиром Анатолійовичем2019