Урок „Застосування похідної“

 

Тема. Застосування похідної.

Мета. Перевірити знання учнями формул для знаходження похідної та вміння застосовувати їх до розв’язування задач; розвивати творче мислення учнів; виховувати наполегливість, уважність і зосередженість.

Тип. Урок-форум

Обладнання. Мультимедійна дошка, картки для індивідуальних завдань

 

 

Хід уроку

 

 

Математика цікава тоді, коли дає

                                                                      поживу нашій винахідливості

                                                               й здатності до міркувань.

 

Д.Пойа

 

 

І Організаційний момент

 

Вдома учні повинні були повторити теоретичний матеріал, що стосується даної теми, а також переглянути у своїх зошитах задачі, які розв’язували на попередніх уроках.

Учнів заздалегідь попереджено про урок-форум і поділено на дві команди, приблизно однакового рівня підготовки. Команди обирають капітанів. На урок запрошують двох експертів-учителів і двох спостерігачів(учнів з паралельних класів).

Форум проводиться у шість турів:

 

І    тур    „Великий ерудит“;

ІІ   тур    „Поспішайте знайти“;

ІІІ  тур    „Вибираємо правильну відповідь“;

ІV  тур    „Малювалки“ ;

V   тур     „Бліц-турнір“;

VІ  тур     „Обганялки“.

 

За підсумками всіх турів експерти та спостерігачі визначають команду-переможницю, а також „щасливчиків“ (учнів, які одержали 12 балів) і „зірок“ першої, другої та третьої величини (учнів, які одержали 15 і більше балів).

Перед початком форуму повідомляється його тема, мета і правила проведення, яких слід дотримуватися; знайомляться присутні з капітанами команд, представляються експерти та спостерігачі.

І    тур    „Великий ерудит“

 

Беруть участь капітани команд, які повідомляють історичну довідку про похідну     (2 б).

Історична довідка.

 

До відкриття похідної незалежно один від одного прийшли два відомих вчених – І.Ньютон і Г. Лейбніц наприкінці Х VІІ ст.

 

 

 

 

 

 

 

 

         Архімед                              І.Ньютон                            Г. Лейбніц

І.Ньютон, означаючи похідну, виходить із задач механіки, а Г. Лейбніц – із геометричних задач. Г. Лейбніц розв’язав задачу про побудову дотичної, а І.Ньютон – прийшов до поняття похідної, виходячи з положень механіки і визначаючи миттєву швидкість під час нерівномірного прямолінійного руху.

Проте ще задовго до цього Архімед розв’язав задачу про побудову дотичної до кривої та знайшов максимум функції

f(x)= x²(a-x)

 

Похідна – це швидкість зміни функції. Нехай матеріальна точка рухається вздовж координатної прямої х за законом х=х(t). Тоді похідна від координати за часом у даний момент є швидкістю руху в цей момент часу. У цьому і полягає її механічний зміст.

У Г. Лейбніца первісним поняттям для похідної була дотична. Існування похідної функції у= f(x) у точці х₀ рівносильне існуванню дотичної (не вертикальної) у даній точці графіка, кутовий коефіцієнт якої дорівнює f'(x₀). Це і є геометричним змістом похідної.

 

ІІ   тур    „Поспішайте знайти“

 

На дошці подана таблиця. Команди повинні визначити, яке завдання „заховане“ в таблиці і виконати його усно. За кожну правильну відповідь команді нараховується 1 бал.

 

№	Функція	?
1	f(x)= х2+cos x	2x-sinx
2	f(x)= sin2x	?
3	f(x)=	?
4	f(x)= ctg x	?
5	f(x)= cos2x cos5x+ sin2x sin5x	?
6	f(x)=	?

 

ІІІ  тур    „Вибираємо правильну відповідь“

 

Для кожної команди на дошку проектується таблиця з тестами. Кожен учень на окремому аркуші записує відповідь. За кожну правильну відповідь учнім нараховується 1 бал. Аркуші здаються на перевірку спостерігачам. Кожен учень одержує свої бали, а команді ставиться середній бал.

Тести.

 

І команда

1. Кутовий коефіцієнт дотичної до графіка функції у= sinx у точці х₀= дорівнює:

а)  ;     б) - ;       в) ;        г)  -.

2. Функція у= - х² +2х-3 спадає на проміжку:

а)  [1; +∞) ;     б)(- ∞; 1];        в) (- ∞;1] [1; +∞);        г)  (-∞;+∞).

3. Для функції у=  х² +2х-3 екстремумом буде:

а) у_max = у(-1)= -4 ;  б) y_min= у(-1)= -4;   в) у_max = у(2)= 7;   г)  y_min= у(-2)= -9.

4. Найбільше і найменше значення функції у= х³ -3х на відрізку [0;2] дорівнює

а) 2 і -2;    б) -2 і 4;     в) 4 і -4;      г) 2 і -4.

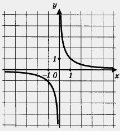
5. На малюнку зображено графік функції

у= f(x). На яких проміжках області визначення функції похідна її від’ємна:

а)   (-∞;+∞);     б) (- ∞; 0) (0; +∞);      

в)  (0; +∞);        г)  інша відповідь.

 

 

ІІ команда

1. Кутовий коефіцієнт дотичної до графіка функції у= соsx у точці х₀= дорівнює:

а)  ;     б) - ;       в) ;        г)  -.

2. Функція у=  х² - 2х+3 зростає на проміжку:

а)  [1; +∞) ;     б)(- ∞; 1];        в) ( -∞;1] [1; +∞);        г)  (-∞;+∞).

3. Для функції у=  - х² +4х+3 екстремумом буде:

а) у_max = у(-1)= -4 ;  б) y_min= у(-1)= -4;   в) у_max = у(2)= 7;   г)  y_min= у(-2)= -9.

4. Найбільше і найменше значення функції у= 6х - 2х³ на відрізку [0;2] дорівнює

а) 2 і -2;    б) -2 і 4;     в) 4 і -4;      г) 2 і -4.

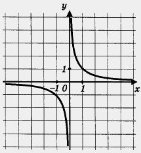
5. На малюнку зображено графік функції

у= f(x). На яких проміжках області визначення функції похідна її додатна:

а)   (-∞;+∞);     б) (- ∞; 0) (0; +∞);      

в)  (0; +∞);        г)  інша відповідь.

 

 

ІV  тур    „Малювалки“

На слайді подано графік функції у= f(x).

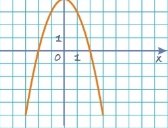
Знайти графік похідної цієї функції:

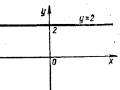
а)

 

 

 

 

 

б)         у                                             в)                        у

 

                               х                                                                 х

                                                                                     -2

 

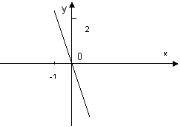
г)

 

 

 

 

 

Команда, яка швидше і правильно виконає завдання, отримає 1 бал.

 

V   тур     „Бліц-турнір“

 

Учні виконують самостійну роботу, яку перевіряють експерти та спостерігачі. Команді нараховується середній бал.

 

Варіант 1.

1 (1б). Точка рухається за законом S(t)=3t² -2t+4, де t – час у секундах, S-переміщення у метрах. Знайти швидкість руху у момент часу t=2.

2(2б). Число 48 подайте у вигляді суми двох додатних чисел так, щоб їх добуток був найбільшим.

Варіант 2.

1 (1б). Точка рухається за законом S(t)=4t² -2t+1, де t – час у секундах, S-переміщення у метрах. Знайти швидкість руху у момент часу t=2.

2(2б). Число 36 подайте у вигляді суми двох додатних чисел так, щоб їх добуток був найбільшим.

 

У цей час по одному сильному учню від команд розв’язують на дошці задачі.

1. Число 54 записане у вигляді суми трьох додатних чисел. Відомо, що перше у 2 рази більше від другого. Знайти ці числа,знаючи, що їх добуток найбільший. (3 бала).

2. Знайти найбільше і найменше значення функції на даному проміжку:

у= 2 sin ² х – соsx, [ -].

 

VІ  тур     „Обганялки“

 

Це тур- естафета, в якій беруть учать по 8 учнів від кожної команди. Їм необхідно дослідити функцію та побудувати її графік. (8 кроків). Кожна правильна відповідь -1 бал.

Перша команда                                       Друга команда

 Дослідити функцію та побудувати її графік:

f(x)=  3х –х³                                                     f(x)= х⁴ -4х²

 

 

Підсумок уроку та оцінювання.

 

Експерти визначають команду-переможницю та оцінюють роботу кожного учня; за кількістю набраних балів визначають „щасливчиків“ та зірок турніру.

 

Відповіді до завдань.

ІІ тур

 

№	Функція	?
1	f(x)= х2+cos x	2x-sinx
2	f(x)= sin2x	2 соs 2x    ?
3	f(x)=	?
4	f(x)= ctg x	-?
5	f(x)= cos2x cos5x+ sin2x sin5x	= (cos3x)'= -3sin3x?
6	f(x)=	= (tg4x)'=?

 

ІІІ тур

 

Варіант 1.     1. в);     2. а);       3. б);         4.  а);       5.    б).

 

Варіант 2.     1. б);     2. а);       3. в);         4.  в);       5.    г).

 

ІV  тур   

г)

 

 

 

 

 

 

V   тур    

Варіант 1.

 

1. S(t)=3t² -2t+4,  t =2с.   ν(t)= S'(t)=6t-2.    ν(2)= 6∙2-2=10(м/с)

2. Нехай перший доданок х, тоді другий – 48-х. Їх добуток П(х)=48х-х².

П'(х)=48-2х. П'(х)=0, 48-2х=0.   2х=48, х=24.

0≤х≤48.  П(0)=0;    П(24)=24∙24=576;      П(48)= 48∙0=0.

Добуток найбільший, якщо кожен з доданків дорівнює 24.

 

Варіант 2.

1. S(t)=4t² -2t+1,  t =2с.    ν(t)= S'(t)=8t-2.    ν(2)= 8∙2-2=14(м/с)

2. Нехай перший доданок х, тоді другий – 36-х. Їх добуток П(х)=36х-х².

П'(х)=36-2х.   П'(х)=0,   36 -2х=0.   2х=36, х=18.

0≤х≤36.  П(0)=0;    П(18)=18∙18=324;      П(36)= 36∙0=0.

Добуток найбільший, якщо кожен з доданків дорівнює 18.

 

Індивідуальні завдання:

 

Картка 1, 2.  (по 3 бала кожне завдання)

1. Нехай друге перше число х, тоді перше 2х, а третє –(54-3х). Їх добуток   П(х)=2х∙х∙(54-3х)= 108х²-6х³.

П'(х)=216х-18х².   

П'(х)=0,  216х-18х²=0.    12х-х²=0,   х(12-х)=0,    х₁=0,  х₂=12.

0≤х≤54.   П(0)=0;    П(12)= 108∙12²-6∙12³= 15552-10368=5184;   П(54)= 108∙54²--6∙54³= 54² (108-324)=2916∙(-216)=-629 856.

Отже, друге число 12, перше  - 24, а третє – 18.

Відповідь. 24; 12; 18.

 

2.  Знайти найбільше і найменше значення функції на даному проміжку:

у= 2 sin ² х – соsx, [ -].

Розв’язання.

 у' =2∙2sin²x cos x+2 sin2x= 4 sin2x.

у' =0,   4 sin2x=0.       sin2x=0;   2x=πn,  nZ,    x=,  nZ.

Проміжку  [ -] належить х=0.

у(-)=2 sin²(-)-cos 2(-)=2∙-0=1;

у(0)= 2 sin²0-cos 0 = -1;

у()=2 sin²-cos =2∙-0=1.

min y = y(0)=-1,      max y= y (-)=y()=1.

[-]                                  [-]

 

 

 

VІ  тур    

 

Варіант 1.

 

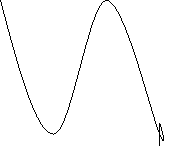
f(x)=  3х –х³                 

 

Розв’язання.

1. D(f)=R

2. Парність. f(-x)=3(-x)-(-x³) = -3x+x³ = -(3x-x³)= -f(x). Отже, функція непарна.

3. Нулі функції: 0;  -;  .

Проміжки знакосталості функції:

    f(x)>0, якщо х (-∞;-) (0; );       f(x)< 0,  якщо х (-;0) (;+∞).

4.    f ' (x)=3-x² = 3(1-х)(1+х).

5. Критичні точки.   f ' (x)=0;   3(1-х)(1+х)=0,   х=1, х=-1.

6. Знаки похідної і поведінка функції на проміжках, на які розбили область визначення критичні точки:

 

f ' (x)         -             +                  -

 

f(x)              -1                    1                     х

 

7. Екстремуми.

 

y_min= y(-1)=-2,      y_max= y(1)=2,     

 

8.   

                                           y

 

 

                                   2

                                   1

 

 

                       -2     -1   0        1    2                   x

                                  -1

                                   -2

 

 

Варіант 2.

 

f(x)= х⁴-4x²                

 

Розв’язання.

1. D(f)=R

2. Парність. f(-x)=(-x)⁴-4(-x)² = x⁴-4x² = f(x). Отже, функція парна.

3. Нулі функції: 0;  -2;  2.

Проміжки знакосталості функції:

    f(x)>0, якщо х (-∞;-2) (2;+ ∞);       f(x)< 0,  якщо х (-2;0) (0;2).

4.    f ' (x)= 4x³ - 8x.

5. Критичні точки.   f ' (x)=0;  4x³ - 8x =0,   х=0, х=-, x=

6. Знаки похідної і поведінка функції на проміжках, на які розбили область визначення критичні точки:

 

f ' (x)         -                 +                  -                   +

 

f(x)                 -                 0                            х

 

7. Екстремуми.

 

y_min= y(-)=y()=-4,      y_max= y(0)=0,     

 

 

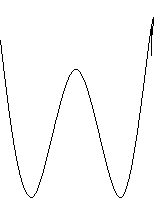8.                                 y

 

 

                                  

                       -2     -1   0        1      2                 x

                                  -1

 

 

 

                                   -4