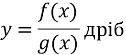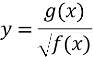Конспект уроку з алгебри для 10 класу на тему: «Перетворення графіків функції»
НАВЧАЛЬНО-МЕТОДИЧНА КАРТА (план) ЗАНЯТТЯ № 5-6
|
Група |
Дата |
|
|
|
|
|
|
Предмет: математика
Тема заняття: Перетворення графіків функції.
Мета заняття:
Освітня: розширити основні відомості про функцію, набуті в основній школі та на попередньому занятті, формувати вміння будувати графіки функцій за допомогою геометричних перетворень; закріпити знання студентів про функції, їх парність та непарність; розвивати логічне мислення, пам'ять, увагу студентів;
Виховна: виховувати інтерес до вивчення точних наук, охайність.
Тип уроку: комбінований
СТРУКТУРА УРОКУ І РОЗРАХУНОК ЧАСУ
- Організаційна частина ………………………………………………………. 2 хв
- Перевірка домашнього завдання, перевірка раніше засвоєних знань.. ……10 хв
- Мотивація навчальної роботи. Повідомлення теми і мети завдань………... 5 хв
- Сприймання та осмислення студентами нового навчального матеріалу…... 35 хв
- Узагальнення і систематизація виучуваного матеріалу…………………….. 15 хв
- Домашнє завдання…………………………………………………………….. 4 хв
- Підведення підсумків заняття…………………………………………...…… 4 хв
МЕТОДИ
Усне опитування, бесіда, робота в групах, пояснювально-ілюстративний метод, здоров’язберігаючі технології, евристична бесіда, «Асоціативний кущ»
ВИЯВЛЕННЯ МІЖПРЕДМЕТНИХ ТА ВНУТРІШНЬОПРЕДМЕТНИХ ЗВЯЗКІВ
Геометрія, економіка, креслення, фізика.
ХІД ЗАНЯТТЯ
- Організаційна частина
Перевірка присутніх/відсутніх студентів на занятті.
- Перевірка домашнього завдання, перевірка раніше засвоєних знань
- Перевірка домашнього завдання.
- Робота в групах. «Заповни таблицю»
|
№ |
Функція |
Область визначення |
|
1 |
(многочлен n-ого степеня) |
|
|
2 |
|
|
|
3 |
|
|
|
4 |
|
|
- Метод «Кубування» (опитування за теоретичним матеріалом попереднього уроку)
- Мотивація навчальної роботи. Повідомлення теми і мети завдань.
Функція є одним із найважливіших понять сучасної математики. Від того, наскільки сумлінно ви засвоїте поняття функції, її Властивості, залежить успішне оволодіння подальшим курсом математики.
- Сприймання і первинне усвідомлення нового матеріалу, осмислення зв’язків і відношень в об’єктах вивчення.
План подання нового матеріалу
1. Квадратична функція
2. Графік функції y=f(x)+b
3. Графік функції y=f(x+a).
4. Графік функції y=kf(x).
5. Графік функції y=f(kx).
6. Графік функції y=f(|x|)
Подання нового матеріалу
Квадратична функція.
Квадратичною називається функція, яка задається формулою ![]() , де а, b, c, - дійсні числа, причому
, де а, b, c, - дійсні числа, причому ![]() .
.
Графіком функції є парабола.
- Координати вершин параболи:
![]()
![]()
- Точки перетину параболи з осями координат.
0у: ![]()
![]()
0x: ![]() ,
, ![]() , треба розв’язати квадратне рівняння і корені будуть точками перетину осі 0х
, треба розв’язати квадратне рівняння і корені будуть точками перетину осі 0х
-
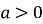 , вітки параболи направлені вгору
, вітки параболи направлені вгору
![]() , вітки параболи направлені вниз.
, вітки параболи направлені вниз.
У 9 класі ви навчилися за допомогою графіка функції ![]() будувати графіки функцій
будувати графіки функцій ![]() ,
, ![]() ,
, ![]() . Нагадаємо правила, які дозволяють виконати такі побудови.
. Нагадаємо правила, які дозволяють виконати такі побудови.
Графік функції ![]() можна отримати в результаті паралельного перенесення графіка функції
можна отримати в результаті паралельного перенесення графіка функції ![]() на b одиниць угору, якщо
на b одиниць угору, якщо ![]() , і на –b одиниць униз, якщо
, і на –b одиниць униз, якщо ![]() .
.
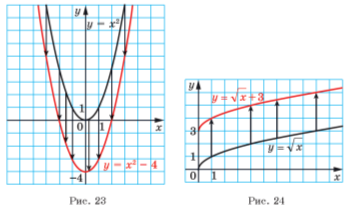
На рисунках 23, 24 показано, як працює це правило для побудови графіків функцій ![]() і
і ![]() .
.
Графік функції ![]() можна отримати в результаті паралельного перенесення графіка функції
можна отримати в результаті паралельного перенесення графіка функції ![]() на a одиниць уліво, якщо
на a одиниць уліво, якщо ![]() , і на –a одиниць управо, якщо
, і на –a одиниць управо, якщо ![]() .
.
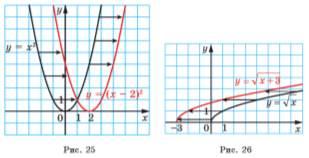
На рисунках 25, 26 показано, як працює це правило для побудови графіків функцій ![]() і
і ![]() .
.
Графік функції ![]() можна отримати, замінивши кожну точку графіка функції
можна отримати, замінивши кожну точку графіка функції ![]() на точку з тією самою абсцисою і ординатою, помноженою на k.
на точку з тією самою абсцисою і ординатою, помноженою на k.
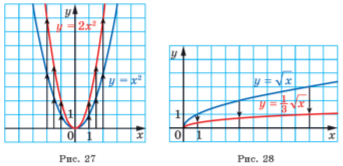
На рисунках 27, 28, 29 показано, як працює це правило для побудови графіків функцій ![]() ,
, ![]() ,
, ![]() і
і ![]() .
.
Кажуть, що графік функції ![]() отримано з графіка функції
отримано з графіка функції ![]() у результаті розтягу в k разів від осі абсцис, якщо
у результаті розтягу в k разів від осі абсцис, якщо ![]() , або в результаті стиску в
, або в результаті стиску в ![]() разів до осі абсцис, якщо
разів до осі абсцис, якщо ![]()
Покажемо, як можна побудувати графік функції ![]() , якщо відомо графік функції
, якщо відомо графік функції ![]() .
.
Розглянемо випадок, коли ![]() . Якщо точка
. Якщо точка ![]() належить графіку функції
належить графіку функції ![]() , то точка
, то точка ![]() належить графіку функції
належить графіку функції ![]() . Справді, при
. Справді, при ![]() маємо:
маємо:
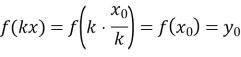
Отже, кожній точці ![]() графіка функції
графіка функції ![]() відповідає єдина точка
відповідає єдина точка ![]() графіка функції
графіка функції ![]() . Аналогічно можна показати (зробіть це самостійно), що кожна точка
. Аналогічно можна показати (зробіть це самостійно), що кожна точка ![]() графіка функції
графіка функції ![]() є відповідною єдиній точці
є відповідною єдиній точці ![]() графіка функції
графіка функції ![]() .
.
Тому графік функції ![]() , де
, де ![]() , можна отримати, замінивши кожну точку графіка функції
, можна отримати, замінивши кожну точку графіка функції ![]() на точку з тією самою ординатою і абсцисою, поділеною на k.
на точку з тією самою ординатою і абсцисою, поділеною на k.
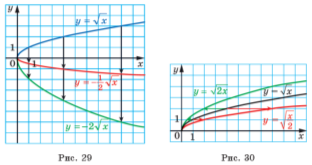
На рисунку 30 показано, як працює це правило для побудови графіків функцій ![]() і
і ![]() . Говорять, що графік функції
. Говорять, що графік функції ![]() отримано з графіка функції
отримано з графіка функції ![]() у результаті стиску в k разів до осі ординат, якщо
у результаті стиску в k разів до осі ординат, якщо ![]() , або в результаті розтягу в
, або в результаті розтягу в ![]() разів від осі ординат, якщо
разів від осі ординат, якщо ![]() .
.
Покажемо, як побудувати графік функції ![]() , якщо відомо графік функції
, якщо відомо графік функції ![]() .
.
Зазначимо, що коли точка ![]() належить графіку функції
належить графіку функції ![]() , то точка
, то точка ![]() належить графіку функції
належить графіку функції ![]() . Дійсно,
. Дійсно, ![]() .
.
Зрозуміло, що між точками графіків функцій ![]() і
і ![]() можна встановити взаємно однозначну відповідність.
можна встановити взаємно однозначну відповідність.
Тоді всі точки графіка функції ![]() можна отримати, замінивши кожну точку графіка функції
можна отримати, замінивши кожну точку графіка функції ![]() на точку, симетричну їй відносно осі ординат, тобто відобразивши графік функції
на точку, симетричну їй відносно осі ординат, тобто відобразивши графік функції ![]() симетрично відносно осі ординат.
симетрично відносно осі ординат.
Таке перетворення графіка функції ![]() називають симетрією відносно осі ординат.
називають симетрією відносно осі ординат.
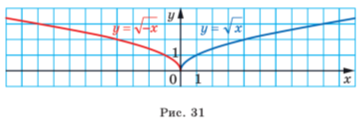
На рисунку 31 показано, як за допомогою графіка функції ![]() побудовано графік функції
побудовано графік функції ![]() .
.
З огляду на сказане стає зрозумілим, що правило побудови графіка функції ![]() , де
, де ![]() , аналогічне випадку, коли
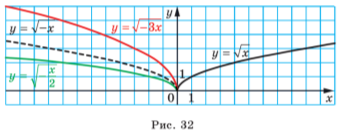
, аналогічне випадку, коли ![]() . Наприклад, на рисунку 32 показано, як можна за допомогою графіка функції
. Наприклад, на рисунку 32 показано, як можна за допомогою графіка функції ![]() побудувати графіки функцій
побудувати графіки функцій ![]() і
і ![]() .
.
Приклад 1. Побудуйте графік функції ![]() .
.
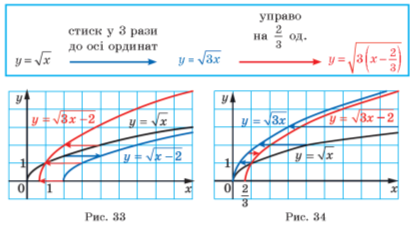
Розв’язання. Схема побудови має такий вигляд (рис. 33):

Якщо задану функцію подати у вигляді ![]() , то побудову графіка можна вести і за такою схемою (рис. 34):
, то побудову графіка можна вести і за такою схемою (рис. 34):
5. Узагальнення і систематизація знань.
1. Вправи з поясненням
1). Дано графік функції у = f(х). Як побудувати графік функції у = -f(х)?
2). Дано графік функції у =f(х). Як побудувати графіки функцій у = 2f(x)та y =1/2f(x)?
2. Розв'язування вправ
Учитель пропонує розв'язати вправи №3(1-3,10,11,15). Студенти усно пояснюють етапи побудови графіків функцій.
Вправа №3(1—3).
Графік функції у =1/х – це гіпербола, яка розташована у І і II чвертях. Графік функції у =1/(х+2) можна дістати переміщенням графіка функції у =1/х на дві одиниці ліворуч вздовж осі Ох. Графік функції у =1/(х-2) можна дістати переміщенням графіка функції у = 1/х на дві одиниці праворуч вздовж осі Ох.
3. Графік якої функції отримаємо, якщо графік функції ![]() паралельно перенесемо:
паралельно перенесемо:
1) на 5 одиниць угору;
3) на 10 одиниць униз;
2) на 8 одиниць управо;
4) на 6 одиниць уліво;
5) на 3 одиниці вправо і на 2 одиниці вниз;
6) на 1 одиницю вліво і на 1 одиницю вгору?
6. Домашнє завдання.
- Підведення підсумків заняття.
Евристична бесіда
-
Як можна отримати графік функції
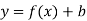 , використовуючи графік функції
, використовуючи графік функції 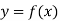 ?
?
-
Як можна отримати графік функції
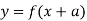 , використовуючи графік функції
, використовуючи графік функції 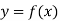 ?
?
-
Як можна отримати графік функції
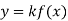 , використовуючи графік функції
, використовуючи графік функції 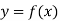 ?
?
-
Як можна отримати графік функції
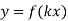 , де
, де 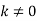 , використовуючи графік функції
, використовуючи графік функції 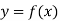 ?
?
|
№ |
Функція |
Область визначення |
|
1 |
(многочлен n-ого степеня) |
|
|
2 |
|
|
|
3 |
|
|
|
4 |
|
|
|
№ |
Функція |
Область визначення |
|
1 |
(многочлен n-ого степеня) |
|
|
2 |
|
|
|
3 |
|
|
|
4 |
|
|
|
№ |
Функція |
Область визначення |
|
1 |
(многочлен n-ого степеня) |
|
|
2 |
|
|
|
3 |
|
|
|
4 |
|
|
|
№ |
Функція |
Область визначення |
|
1 |
(многочлен n-ого степеня) |
|
|
2 |
|
|
|
3 |
|
|
|
4 |
|
|

про публікацію авторської розробки
Додати розробку