"Розробка структурних тематичних схем до уроків алгебри і початків аналізу для 10 класу"
Розробка структурних тематичних схем
для використання на уроках алгебри та початків аналізу для 10 класу
Вчитель вищої категорії Шевчук А.В.
Київ-2019
Дослідження функції на парність та непарність за
схемою
|
Дана за умовою функція у = f (x) визначена на D(f)
|
|
Перевіряємо виконання формул |
|
Якщо область визначення D(f) симетрична відносно точки (0;0)
|
|
Якщо область визначення не симетрична відносно точки (0;0), то функція не парна ні непарна.
|
Якщо f( - x) = f(x), то функція парна;
Якщо f( - x) = - f(x), то функція непарна;
Якщо f( - x) ≠ f(x) і f( - x) ≠ -f(x) то функція ні парна ні непарна.
Ірраціональні рівняння та їх розв'язки за схемою
п√f( х) = п√g( х) ; п√f( х) = g( х) ; п√f( х) = a
n= 2k n=2k+1
Визначити D(f)
Піднести до степеня п ліву і праву частини рівняння, розв'язати
Обов'язково зробити перевірку,
відкинути сторонні корені.
Записати відповідь.
Знаки тригонометричних функцій в одиничному колі
за схемами
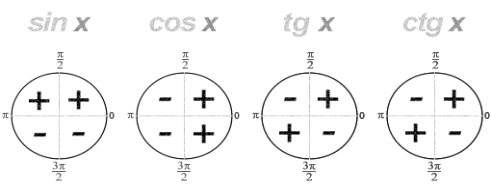
Степінь з раціональним показником за таблицями
Вираз am/n означає корінь, показник якого дорівнює знаменнику n дробу m/n, а
показник степеня підкореневого числа дорівнює чисельнику m дробу m/n, тобтоn√ аm
am/n =n√ аm , а>0
За означенням: 111/2 = √11
Приклади:
1. Обчисли: 321/5
Розв'язання
321/5 =5√32=2
2. Обчисли: (−27)1/3
Розв'язання
Степінь із дробовим показником для випадку від'ємної основи не має змісту.
Зверни увагу!
Слід звернути увагу на те, що основа не може бути від'ємним числом,
am/n (а>0), а показник степеня може бути як додатним, так і від'ємним.
Приклади:
Проаналізуємо два рівняння.
1. Розв'яжи рівняння: 3√ у2 =1
Розв'язання
Піднесемо обидві частини рівняння до куба:
у2=1;
y1,2= ±1
Відповідь: −1;1
2. Розв'яжи рівняння: y2/3=1
Розв'язання
Основа y повинна бути невід'ємною, тому вона підноситься до дробового степеня.
Піднесемо обидві частини рівняння до куба:
у2=1;
y1,2= ±1;
y>0;
у=1
Отже, зі знайдених вище двох значень y коренем рівняння є лише значення y=1.
Відповідь: 1
Проаналізуємо розв`язки двох рівнянь.
|
№1 Рівняння з коренем 3-го степеня
|
№2 Рівняння зі степенем1/3 |
|
3√ 2x - 1 =3√ 5 -х ; За властивістю функції у =3√ х ОДЗ:R
2х – 1= 5 – х; 3х = 6: х=2. Відповідь: 2
|
(2х – 1)1/3 =(5-х)1/3;
ОДЗ: {2х – 1>0; 5 – x>0; : {х >0,5; x< -5 Ø
Відповідь: розв'язків немає
|
Якщо p/q — звичайний дріб, де q≠1 і a>0, то під a−p/q розуміють 1/ap/q.
a−p/q=1/ap/q
Наприклад: 7−1/2=1/ 71/2=1/√7
Графіки степеневих функцій
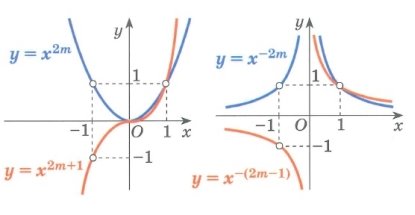
Тема: «Найбільше та найменше значення функції y=(f(x)
на проміжку [a ;b] »
про публікацію авторської розробки
Додати розробку